苏科版八年级数学上册 6.1 函数(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 6.1 函数(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 08:44:51 | ||
图片预览







文档简介
(共20张PPT)
时间是个常数,但对勤奋者来说,是个“变数”。用“分”来计算时间的人比用“小时”来计算时间的人时间多59倍。
----雷巴柯夫
6.1 函数(1)
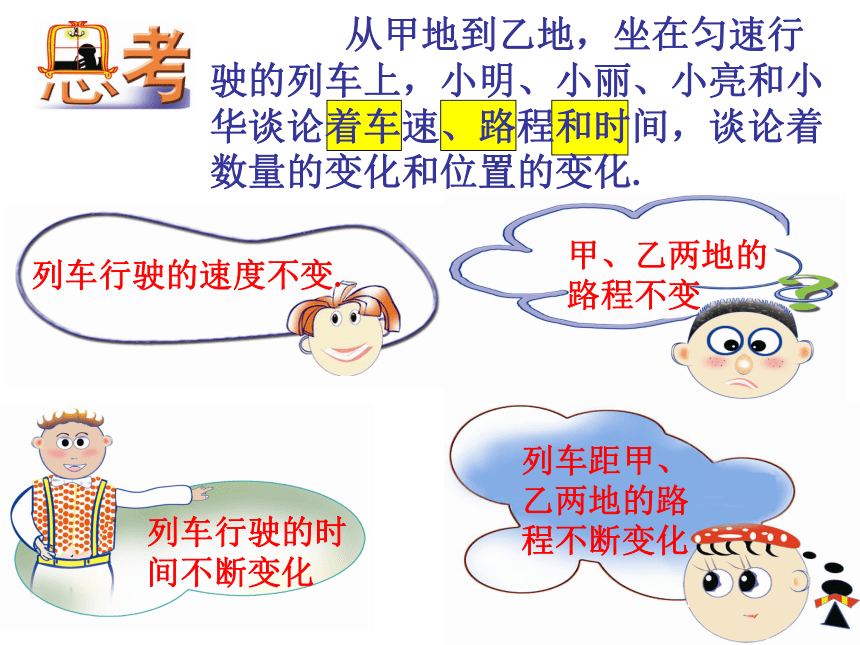
甲地到乙地,坐在匀速行驶的列车上,小明、小丽、小亮和小华谈论着车速、路程和时间,谈论着数量的变化和位置的变化.
你知道在这一过程中,哪些量发生了改变?那些量没有发生改变?
从甲地到乙地,坐在匀速行驶的列车上,小明、小丽、小亮和小华谈论着车速、路程和时间,谈论着数量的变化和位置的变化.
列车行驶的速度不变.
甲、乙两地的路程不变
列车行驶的时间不断变化
列车距甲、乙两地的路程不断变化
在某一变化过程中,数值保持不变的量叫做常量.
如在上面的过程中,列车行驶的速度,甲、乙两地的路程都始终保持同一数值,像这样数值保持不变的量叫做常量.
在某一变化过程中,数值保持不变的量叫做常量.
如在上面的过程中,列车行驶的速度,甲、乙两地的路程都始终保持同一数值,像这样数值保持不变的量叫做常量.
在某一变化过程中,可以取不同数值的量叫做变量.
如在上面的过程中,列车行驶的时间;列车与甲、乙两地间的路程不断变化,像这样可以取不同数值的量叫做变量.
商场所售的某种大米的单价是2.7元/千克.
1、在某一段售米过程中,什么量是不变的?什么量是变化的?
2、小明的妈妈买了20千克大米,应当付多少钱?
3、如果某顾客所买数量用n来表示,所付的钱数用m来表示,那么你能得到一个怎样的关系式?
单价
买米的重量和总价
54元
m=2.7n
变量为m、n,常量为2.7
1.多边形内角和β与边数n之间的关系是: β=(n-2)·180°,则变量是________.
2.如果用r表示圆的半径,c表示圆的周长, 那么有c=2 π r,在这个问题中有___个 变量,它们是__________.
β与n
两
c和 r
序号 问 题 数量关系 常量 变量
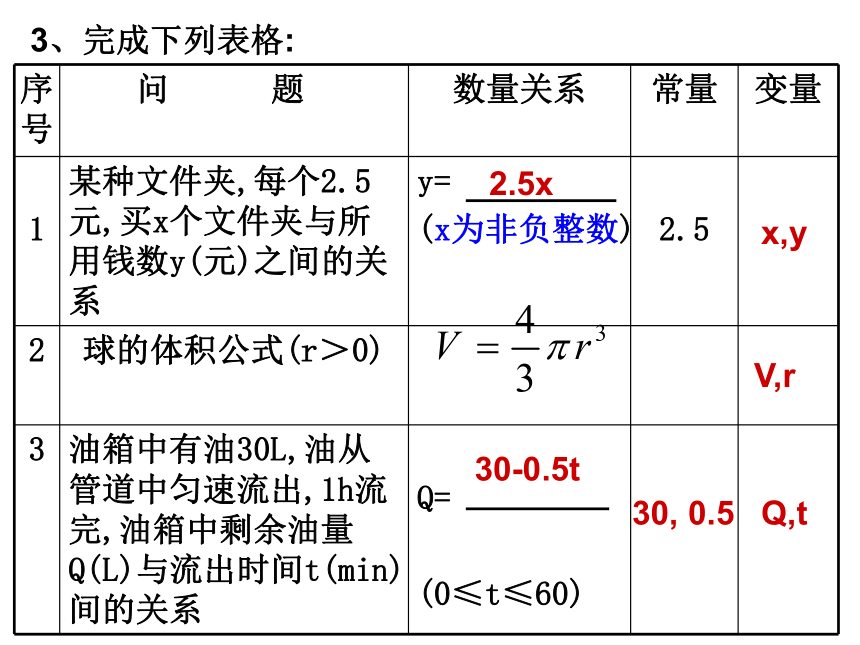
1 某种文件夹,每个2.5元,买x个文件夹与所用钱数y(元)之间的关系 y=
(x为非负整数)
2.5
2 球的体积公式(r>0)
3 油箱中有油30L,油从管道中匀速流出,1h流完,油箱中剩余油量Q(L)与流出时间t(min)间的关系
Q=
(0≤t≤60)
3、完成下列表格:
2.5x
x,y
V,r
30-0.5t
30, 0.5
Q,t
工作人员将水库的水位变化与水库蓄水量变化情况列成如下表格:
水位/m 106 120 133 135 …
蓄水
/m3 2.03×107
7.09×107 1.18×108 1.23×108 …
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
即水库蓄水量随着水位的变化而变化.
搭1条小鱼需要___根火柴,每增加1条小鱼就要增加___根火柴.随着________的增加,____的根数也随着增加.搭n条小鱼与所需的火柴根数s之间的关系为____________.
火柴的根数随着小鱼条数的变化而变化,当小鱼条数确定时,火柴的根数也确定.
8
6
小鱼条数
火柴
s=8+6(n-1)
水中扩散的波纹可以看成是一个不断变化的圆.
它的面积随着 的变化而变化,
随着 的确定而确定.
半径
半径
在上述例子中,每个变化过程都存在着 个变量,当其中一个变量变化时,另一个变量也随着 . 当一个变量确定时,另一个变量有 .
两
发生变化
唯一的值与之对应
一般地,设在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们称y是x的函数.其中,x是自变量,y是因变量.
函数
在一个变化的过程中
两个变
量x和y
对于变量x的每一个值,变量y
都有唯一的值与它对应
一般地,设在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们称y是x的函数.其中,x是自变量,y是因变量.
函数
则水库蓄水量是水位的函数;
1、若水库蓄水量随着水位的变化而变化,
2、若火柴的根数随着小鱼条数的变化而变化,
则 是 的函数;
火柴的根数
小鱼条数
面积
半径
半径
则 是 的函数.
3、圆的面积随着 的变化而变化,
序号 问 题 数量关系 自变量 因变量
1 某种文件夹,每个2.5元,买x个文件夹与所用钱数y(元)之间的关系 y=
(x为非负整数)
2 球的体积公式(r>0)
3 油箱中有油30L,油从管道中匀速流出,1h流完,油箱中剩余油量Q(L)与流出时间t(min)间的关系
Q=
(0≤t≤60)
2.5x
y
V
30-0.5t
Q
x
r
t
下列变量间的关系是不是函数关系 说明理由.
(1)矩形的宽是6cm,它的长与面积;
(2)等腰三角形的底边长是8cm,它的腰长与周长;
(3)圆锥的高一定,它的底面半径与体积.
是函数关系;
是函数关系;
是函数关系.
下列各式中,X都是自变量,Y是不是X的函数,为什么?
(1) Y= X2 + 3
(2) Y2 = X + 3
是函数关系;
不是函数关系;因为当X取值时(如1),Y可取2或-2
用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少
(2)当长方形的宽为0.2m时,长为多少
(3)长方形的长是宽的函数吗 为什么
答: (1)当长方形的宽为0.1m时,长为0.4m;
(2)当长方形的宽为0.2m时,长为0.3m;
(3)长方形的长是宽的函数,
因为周长一定, 当宽变化时,长总有惟一值与它对应.
按图示的运算程序,输入一个实数x便可输出一个相应的实数y.输出值y是输入值x的函数吗 为什么
输入x
+2
×5
-4
输出y
答:输出值y是输入值x的函数, 关系式可表示为:y=5(x+2)-4.
理由:当x变化时,变量y总有惟一值与x对应.
1.知道什么是常量、变量;
2.初步理解函数的概念,能判断两个变量间的关系是不是函数关系.
课堂小结
本节课,你有哪些收获?
时间是个常数,但对勤奋者来说,是个“变数”。用“分”来计算时间的人比用“小时”来计算时间的人时间多59倍。
----雷巴柯夫
6.1 函数(1)
甲地到乙地,坐在匀速行驶的列车上,小明、小丽、小亮和小华谈论着车速、路程和时间,谈论着数量的变化和位置的变化.
你知道在这一过程中,哪些量发生了改变?那些量没有发生改变?
从甲地到乙地,坐在匀速行驶的列车上,小明、小丽、小亮和小华谈论着车速、路程和时间,谈论着数量的变化和位置的变化.
列车行驶的速度不变.
甲、乙两地的路程不变
列车行驶的时间不断变化
列车距甲、乙两地的路程不断变化
在某一变化过程中,数值保持不变的量叫做常量.
如在上面的过程中,列车行驶的速度,甲、乙两地的路程都始终保持同一数值,像这样数值保持不变的量叫做常量.
在某一变化过程中,数值保持不变的量叫做常量.
如在上面的过程中,列车行驶的速度,甲、乙两地的路程都始终保持同一数值,像这样数值保持不变的量叫做常量.
在某一变化过程中,可以取不同数值的量叫做变量.
如在上面的过程中,列车行驶的时间;列车与甲、乙两地间的路程不断变化,像这样可以取不同数值的量叫做变量.
商场所售的某种大米的单价是2.7元/千克.
1、在某一段售米过程中,什么量是不变的?什么量是变化的?
2、小明的妈妈买了20千克大米,应当付多少钱?
3、如果某顾客所买数量用n来表示,所付的钱数用m来表示,那么你能得到一个怎样的关系式?
单价
买米的重量和总价
54元
m=2.7n
变量为m、n,常量为2.7
1.多边形内角和β与边数n之间的关系是: β=(n-2)·180°,则变量是________.
2.如果用r表示圆的半径,c表示圆的周长, 那么有c=2 π r,在这个问题中有___个 变量,它们是__________.
β与n
两
c和 r
序号 问 题 数量关系 常量 变量
1 某种文件夹,每个2.5元,买x个文件夹与所用钱数y(元)之间的关系 y=
(x为非负整数)
2.5
2 球的体积公式(r>0)
3 油箱中有油30L,油从管道中匀速流出,1h流完,油箱中剩余油量Q(L)与流出时间t(min)间的关系
Q=
(0≤t≤60)
3、完成下列表格:
2.5x
x,y
V,r
30-0.5t
30, 0.5
Q,t
工作人员将水库的水位变化与水库蓄水量变化情况列成如下表格:
水位/m 106 120 133 135 …
蓄水
/m3 2.03×107
7.09×107 1.18×108 1.23×108 …
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
即水库蓄水量随着水位的变化而变化.
搭1条小鱼需要___根火柴,每增加1条小鱼就要增加___根火柴.随着________的增加,____的根数也随着增加.搭n条小鱼与所需的火柴根数s之间的关系为____________.
火柴的根数随着小鱼条数的变化而变化,当小鱼条数确定时,火柴的根数也确定.
8
6
小鱼条数
火柴
s=8+6(n-1)
水中扩散的波纹可以看成是一个不断变化的圆.
它的面积随着 的变化而变化,
随着 的确定而确定.
半径
半径
在上述例子中,每个变化过程都存在着 个变量,当其中一个变量变化时,另一个变量也随着 . 当一个变量确定时,另一个变量有 .
两
发生变化
唯一的值与之对应
一般地,设在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们称y是x的函数.其中,x是自变量,y是因变量.
函数
在一个变化的过程中
两个变
量x和y
对于变量x的每一个值,变量y
都有唯一的值与它对应
一般地,设在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,我们称y是x的函数.其中,x是自变量,y是因变量.
函数
则水库蓄水量是水位的函数;
1、若水库蓄水量随着水位的变化而变化,
2、若火柴的根数随着小鱼条数的变化而变化,
则 是 的函数;
火柴的根数
小鱼条数
面积
半径
半径
则 是 的函数.
3、圆的面积随着 的变化而变化,
序号 问 题 数量关系 自变量 因变量
1 某种文件夹,每个2.5元,买x个文件夹与所用钱数y(元)之间的关系 y=
(x为非负整数)
2 球的体积公式(r>0)
3 油箱中有油30L,油从管道中匀速流出,1h流完,油箱中剩余油量Q(L)与流出时间t(min)间的关系
Q=
(0≤t≤60)
2.5x
y
V
30-0.5t
Q
x
r
t
下列变量间的关系是不是函数关系 说明理由.
(1)矩形的宽是6cm,它的长与面积;
(2)等腰三角形的底边长是8cm,它的腰长与周长;
(3)圆锥的高一定,它的底面半径与体积.
是函数关系;
是函数关系;
是函数关系.
下列各式中,X都是自变量,Y是不是X的函数,为什么?
(1) Y= X2 + 3
(2) Y2 = X + 3
是函数关系;
不是函数关系;因为当X取值时(如1),Y可取2或-2
用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少
(2)当长方形的宽为0.2m时,长为多少
(3)长方形的长是宽的函数吗 为什么
答: (1)当长方形的宽为0.1m时,长为0.4m;
(2)当长方形的宽为0.2m时,长为0.3m;
(3)长方形的长是宽的函数,
因为周长一定, 当宽变化时,长总有惟一值与它对应.
按图示的运算程序,输入一个实数x便可输出一个相应的实数y.输出值y是输入值x的函数吗 为什么
输入x
+2
×5
-4
输出y
答:输出值y是输入值x的函数, 关系式可表示为:y=5(x+2)-4.
理由:当x变化时,变量y总有惟一值与x对应.
1.知道什么是常量、变量;
2.初步理解函数的概念,能判断两个变量间的关系是不是函数关系.
课堂小结
本节课,你有哪些收获?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
