直线与圆-基础练(Word含答案解析)
文档属性
| 名称 | 直线与圆-基础练(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 11:16:04 | ||
图片预览




文档简介
2.1.1 直线的倾斜角与斜率
基础练
一、单选题
1.直线 3x y 1 0的倾斜角是( )
3 2 5
A. B. C. D.
4 3 4 6
2.已知直线 l经过点 A 1,3 ,B 2, 5 ,则直线 l的斜率为( )
8 8A. B. C.2 D.3 23
3.如果过 P(-2,m),Q(m,4)两点的直线的斜率为 1,那么 m 的值是( )
A.1 B.4 C.1 或 3 D.1或 4
4.已知直线 l经过两点O(0,0), A(1, 3),直线m的倾斜角是直线 l的倾斜角的两倍,则直线m的斜率是( )
A 3 3. 3 B. C. D. 3
3 3
5.过点 2,1 且倾斜角比直线 y x 1 的倾斜角小 的直线方程是( )
4
A. x 2 B. y 1 C. x 1 D. y 2
6.下列各直线中,与直线2x y 3 0相交的是( )
A.2ax ay 6 0 a 0 B. y 2x
C.2x y 3 0 D.2x y 5 0
二、填空题
7.若直线 x 1的倾斜角为 ,则 的弧度数是________.
8.已知点 A 1,3 ,点B 3,9 ,则直线 AB 的斜率为__________.
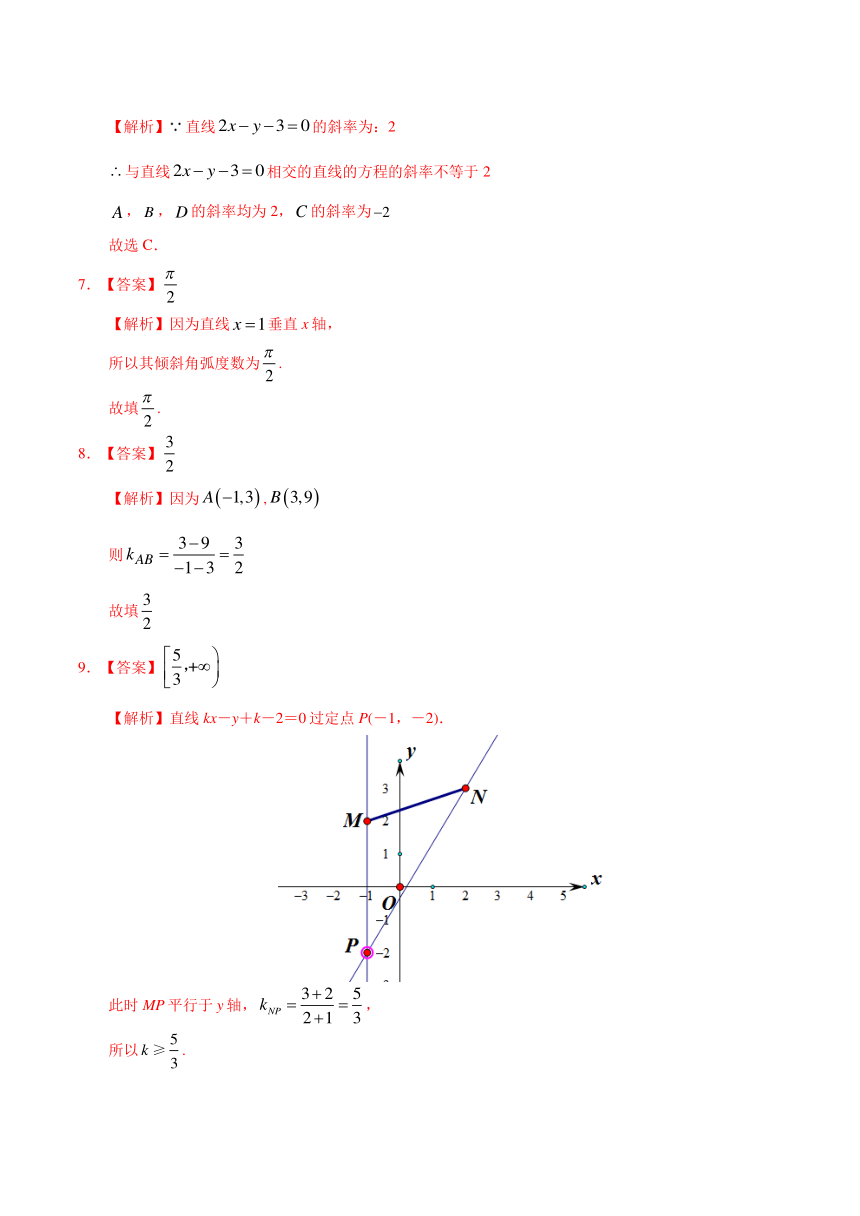
9.已知线段MN 两端点的坐标分别为 M(-1,2)和 N(2,3),若直线 kx-y+k-2=0 与线段MN 有交点,
则实数 k的取值范围是________.
三、解答题
10.(1)求经过下列两点的直线的斜率,并判断其倾斜角是锐角、直角还是钝角.
① 3,5 , 0,2 ;
② 4,4 , 4,5 ;
③ m, 2 3m 3 , 2m 1,3 3m m 1 .
(2)已知点 A 3, 5 , B 1,3 ,C 5,11 .求证:A,B,C 三点共线.
参考答案
1.【答案】B
【解析】设直线的倾斜角为 ,
因为直线方程为 3x y 1 0,所以直线的斜率为 3 ,
所以 tan 3 ,
因为 [0, ),所以 2 ,
3
故选 B
2.【答案】A
5 3 8
【解析】因为直线 l经过点 A 1,3 , B 2, 5 ,所以直线 l 的斜率为 .
2 1 3
故选 A.
3.【答案】A
【解析】由题意,过过 P(-2,m),Q(m,4)两点的直线的斜率为 1,
4 m
根据直线的斜率公式,可得 1,解得
m ( 2) m 1
.
故选 A.
4.【答案】A
k 3 0
2
【解析】依题意 OA 3,所以直线 l的倾斜角为 ,所以直线m 的倾斜角为 ,所以直1 0 3 3
线m 的斜率为 tan 2 3 .
3
故选 A
5.【答案】A
3
【解析】直线 y x 1的斜率为 1,倾斜角为 ,故比它的倾斜角小 的直线的倾斜角为 ,
4 4 2
再根据此直线过点 2,1 ,故要求的直线的方程为 x 2 .
故选 A.
6.【答案】C
【解析】 直线2x y 3 0的斜率为:2
与直线2x y 3 0相交的直线的方程的斜率不等于 2
A, B ,D的斜率均为 2,C 的斜率为 2
故选 C.
7.【答案】
2
【解析】因为直线 x 1垂直 x轴,
所以其倾斜角弧度数为 .
2
故填 .
2
3
8.【答案】
2
【解析】因为 A 1,3 , B 3,9
3 9 3
则 kAB 1 3 2
3
故填
2
5
9.【答案】 ,+ 3
【解析】直线 kx-y+k-2=0过定点 P(-1,-2).
3 2 5
此时 MP 平行于 y轴, kNP ,2 1 3
5
所以 k ≥ .
3
5
故填 ,+ . 3
10.【答案】(1)①钝角,②直角,③锐角;(2)证明见解析
2 5
【解析】(1)① k 1 00 3 ,倾斜角为钝角;
②k不存在,倾斜角为直角;
3 3m 2 3m 3
k 3m 3③ 3 0,倾斜角为锐角.
2m 1 m m 1
3 5 11 3
(2)证明: kAB 2 , k 2 ,且 AB,BC 都经过点 B,1 3 BC 5 1
A,B,C 三点共线.
2.1.2 两条直线平行与垂直的判定
基础练
一、单选题
1.直线ax y 1 0与直线2x 3y 2 0平行,则实数 a的值为( )
2 3
A. B. 1 C. D.6
3 2
2.“a=1”是“直线 x+y=0 和直线 x-ay=0 互相垂直”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.若直线 a,b 的斜率分别为方程 x2 4x 1 0的两个根,则 a与 b的位置关系为( )
A.互相平行 B.互相重合 C.互相垂直 D.无法确定
4.若直线ax 3y 1 0与 x y 4 0互相垂直,则 a 的值为( )
1 2
A.1 B. C. D. 3
2 3
5.已知直线 l1 : x 2ay 1 0,与 l2 : 2a 1 x ay 1 0 平行,则a的值是( )
1 1 1
A.0 或 1 B.1 或 C.0 或 D.
4 4 4
6.已知直线mx 4y 2 0与2x 5y n 0互相垂直,垂足为P 1, p ,则m n p的值是( )
A.24 B.20 C.0 D. 4
二、填空题
7.若直线 l1 : ax 3y 5 0与 l2 : x 2y 1 0互相垂直,则实数a的值为________.
8.已知直线 l :mx y 1 0,若直线 l 与直线 x my 1 0平行,则 m 的值为__________.
9.已知点 A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线 AB 与直线 CD平行,则 m 的值为_______;
三、解答题
10.已知直线 l1 : x my 6 0, l2 : m 2 x 3y 2m 0 .
(1)若 l1 l2 ,求m 的值;
(2)若 l1 / /l2 ,求m 的值.
参考答案
1.【答案】A
【解析】因为直线ax y 1 0与直线2x 3y 2 0平行,
所以 a 2 2 a ,
3 3
故选 A.
2.【答案】C
【解析】直线 x y 0和直线 x ay 0互相垂直的充要条件是1 ( a) 1 1 0,即 a 1,
故选 C
3.【答案】C
【解析】由题意 kakb 1,∴两直线垂直.
故选 C.
4.【答案】D
【解析】∵直线ax 3y 1 0与直线 x y 4 0互相垂直,
∴斜率之积等于 1,
a
∴ 1 1,得a 3 .
3
故选 D.
5.【答案】C
【解析】由题意得:1 ( a) (2a 1) 2a 0, a 0 1或a ,
4
故选 C.
6.【答案】B
【解析】∵两直线互相垂直,∴k1·k2=-1,
m 2
∴- · =-1,∴m=10.又∵垂足为(1,p),
4 5
∴代入直线 10x+4y-2=0 得 p=-2,
将(1,-2)代入直线 2x-5y+n=0得 n=-12,
∴m-n+p=20.
故选 B.
7.【答案】 6
【解析】两直线 l1 : ax 3y 5 0与 l2 : x 2y 1 0互相垂直.
所以a 1 3 2 0,解得a 6
故填 6
8.【答案】 1
【解析】因为直线 l与直线 x my 1 0平行,
m ( m) 1 1 m 1
所以有 m 1 .
m ( 1) 1 1
m 1
故填 1
9.【答案】0或 1
【解析】当m 0时,直线 AB 方程为 x 0,直线CD方程为 x 1,两直线平行,
k m 4 3 m 1 2 0 2 m 1 2当m 0时, AB ,k2m m m CD
,由 得m 1,此时直线 AB 方
m 1 1 m m m
程为 y 3 2(x 1),即 y 2x 1,直线CD方程为 y 2(x 1) ,即 y 2x 2 ,两直线平行.
故填 0 或 1.
10.【答案】(1)m 1 ;(2)m 1
2
【解析】(1)∵直线 l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,
由 l1⊥l2 ,可得 1×(m﹣2)+m×3=0 1,解得m .
2
(2)由题意可知 m 不等于 0,
由 l1∥l m 2 3 2m2 可得 ,解得 m=﹣1.
1 m 8
2.2.1 点斜式方程
基础练
一、单选题
2
1.过点 3,2 ,斜率是 的直线方程是( )
3
2
A. y x 2 4 B. y x 2 C.2x 3y 0 D.3x 2y 0
3 3
2.方程 y y0 k x x0 ( )
A.可以表示任何直线 B.不能表示过原点的直线
C.不能表示与 y 轴垂直的直线 D.不能表示与 x 轴垂直的直线
3.过点 2,0 且与直线 y 2x 5垂直的直线 l 的方程是( )
A. y 2x 4 B. y 2x 4 1C. y x 1 1D. y x 1
2 2
4.已知直线 l过点 2,0 ,且与直线 y 2x 1平行,则直线 l 的方程为( )
A. y 2x 4 B. y 2x 4 C. y 2x 4 D. y 2x 4
5.已知 A 5,2 , B 1,4 ,则 AB 的垂直平分线方程为( )
A. x 3y 7 0 B.3x y 3 0 C.3x y 7 0 D.3x y 7 0
6.过点 A(1,2)且与原点距离最大的直线方程是( )
A. x 2y 5 0 B.2x y 4 0 C. x 3y 7 0 D.3x y 5 0
二、填空题
7.直线 l过点M 1, 2 ,倾斜角为60 .则直线 l的斜截式方程为______________.
8.已知 ABC的三个顶点 A(2,3),B(4, 1),C( 2, 9),若点D, E 分别是边 AB, AC 的中点,则线段DE
所在直线的点斜式方程是________________.
9.已知点 P1(2,3)、P2(-4,5)和 A(-1,2),则过点 A 且与点 P1、P2距离相等的直线方程为______.
三、解答题
10.求适合下列条件的直线方程:
1 A 1, 3 y 3( )经过点 ,倾斜角等于直线 x 的倾斜角的2倍;
3
(2)经过点B 3,4 ,且与两坐标轴围成一个等腰直角三角形.
参考答案
1.【答案】C
【解析】∵直线过点 3,2 2且斜率为 ,
3
由直线方程的点斜式得: y 2 2 (x 3) ,
3
整理得:2x 3y 0 .
故选 C.
2.【答案】D
【解析】因为直线的点斜式方程不能表示斜率不存在的直线,
所以 y y0 k x x0 不能表示与 x 轴垂直的直线,
故选 D。
3.【答案】D
【解析】因为所求直线与直线 y 2x 5垂直,
1
所以其斜率为 k ,
2
又所求直线过点 2,0 ,
1 1
因此,所求直线方程为: y x 2 ,即 y x 1 .
2 2
故选 D.
4.【答案】C
【解析】 直线 l与直线 y 2x 1平行,
直线 l的斜率与 y 2x 1的斜率相等,即直线 l的斜率:k 2;
又 直线 l过点 2,0 ,
则由点斜式可知直线方程为 y 0 2 x 2
整理可得: y 2x 4
故选 C.
5.【答案】B
【解析】设线段 AB 的中点坐标为 x, y ,
5 1
则 x 2, y
2 4
3,中点坐标为 2,3 ,
2 2
k 4 2 1直线 AB 的斜率 ,
1 5 3
AB垂直平分线的斜率为 3,
则 AB 的垂直平分线方程为 y 3 3 x 2 ,
化简得3x y 3 0,
故选 B.
6.【答案】A
【解析】由题知:过点 A(1,2)且与原点距离最大的直线为过点 A(1,2)且与OA垂直的直线.
k 2 y 2 1因为 OA ,故所求直线为 x 1 ,即 x 2y 5 0 .2
故选 A
7.【答案】 y 3x 3 2
【解析】 直线 l的倾斜角为60 , 直线 l的斜率k tan 60 3 ,
又因为直线 l过点M 1, 2 ,所以直线 l的方程为 y 2 3 x 1 ,即 y 3x 3 2,
所以直线 l的斜截式方程为 y 3x 3 2 .
故填 y 3x 3 2 .
4
8.【答案】 y 3 (x 0) y 1 4 或者 (x 3)
3 3
【解析】因为 A(2,3),B(4, 1),C( 2, 9),点D, E 分别是边 AB, AC 的中点,
所以D(3,1),E(0, 3),
1 ( 3) 4
直线DE 的斜率为 ,
3 0 3
4 4
所以线段DE 所在直线的点斜式方程是 y 3 (x 0) 或者 y 1 (x 3) .
3 3
故填 y 3
4
(x 0) 4或者 y 1 (x 3)
3 3
9.【答案】x+3y﹣5=0或 x=﹣1.
【解析】①当直线与点 P1,P2的连线平行时,
3 5 1
由直线 P1P2的斜率 k ,
2 4 3
1
所以所求直线方程为 y﹣2 (x+1),
3
即 x+3y﹣5=0;
②当直线过线段 P1P2的中点时,
因为线段 P1P2的中点为(﹣1,4),
所以直线方程为 x=﹣1.
∴所求直线方程为 x+3y﹣5=0或 x=﹣1,
故答填 x+3y﹣5=0 或 x=﹣1.
10.【答案】(1) 3x y 3 3 0(2) x y 1 0或 x y 7 0.
2 tan
【解析】(1)已知 tan = 3 , k tan 2 2 33 1 tan
直线方程为 y 3 3(x 1)化简得 3x y 3 3 0
(2)由题意可知,所求直线的斜率为 .
又过点 3,4 ,由点斜式得 y 4 x 3 ,
所求直线的方程为 x y 1 0或 x y 7 0.
2.2.2 两点式方程
基础练
一、单选题
1.过 1, 2 , 5,3 的直线方程是( )
y 2 x 1 y 2 x 1 y 1 x 3 x 2 y 3
A. B. C. D.
5 1 3 1 3 2 5 1 5 1 5 3 5 2 2 3
2.已知三角形三个顶点 A 5,0 , B 3, 3 ,C 0,2 ,则 BC 边上中线所在直线方程是( )
A. x 13y 5 0 B. x 13y 5 0 C. x 13y 5 0 D. x 13y 0
3.经过点 A(2,5) , B( 3,6) 的直线在 x 轴上的截距为( )
A.2 B. 3 C. 27 D.27
4.下列命题中,真命题的序号是( )
A.经过定点P0 x0 , y0 直线都可以用方程 y y0 k x x0
x y
B.不经过原点的直线都可以用方程 1表示;
a b
C.过任意不同两点 P1 x1, y1 、P2 x2 , y2 的直线都可以用方程 y y1 x2 x1 x x2 y2 y1
D.经过 A 0,b 的直线都可以用方程 y kx b表示
5.已知 ABC的三个顶点为 A(1,2),B(3,6) ,C(5,2),M 为 AB 的中点,N 为 AC 的中点,则中位线MN
所在直线方程为( )
A.2x y 8 0 B.2x y 8 0
C.2x y 12 0 D.2x y 12 0
6.已知△ABC的三个顶点分别为 A 2,8 ,B 4,0 ,C 6,0 ,则过点 B 将 ABC的面积平分的直线方
程为( )
A.2x y 4 0 B. x 2y 4 0
C.2x y 4 0 D. x 2y 4 0
二、填空题
7.一条光线从点P(6,4)射出,与 x 轴相较于点Q(2,0),经 x 轴反射,则反射光线所在的直线方程为______
8.已知 ABC的三个顶点分别为 A 1,2 , B 4,1 ,C 3,6 ,则 AC 边上的中线BM 所在直线的方程为
______.
9.两条直线 l1:a1x b1y 1 0和 l2 :a2x b2 y 1 0相交于点 P 5, 6 ,则过点 A a1,b1 ,B a2 ,b2
的直线方程为_______
三、解答题
10.已知△ABC的三个顶点 A(1,1) ,B(2,0),C(4,4) .
(1)求 AB 边所在直线的方程;
(2)求BC 边上中线所在直线的方程.
参考答案
1.【答案】B
【解析】因为所求直线过点 1, 2 , 5,3 ,
y 2 3 2 y 2 x 1
所以 ,即 .
x 1 5 1 3 2 5 1
故选 B
2.【答案】C
【解析】 B 3, 3 ,C 0,2 0 3 2 3 3 1, BC 中点的坐标为( , ),即( , ).
2 2 2 2
3 1
则 BC 边上的中线应过 A 5,0 , , 2 2 两点,
y x 5
由两点式得: 0 1 3 5 ,整理,得
x 13y 5 0.
2 2
故选 C.
3.【答案】D
【解析】由两点式得直线方程为=,即 x+5y-27=0,令 y=0 得 x=27.
故选 D.
4.【答案】C
【解析】对 A,当经过定点P0 x0 , y0 直线垂直于 x 轴时不成立.故 A 错误.
x x y对 B, 直线垂直于 轴时不可以用方程 1表示.故 B 错误.
a b
y y
对 C,当直线P1P2 斜率存在时,方程为 y y1
2 1 x x
x x 2 成立
.
2 1
当直线P1P2 斜率不存在时 x1 x2 ,方程为 x x2 成立.故 C 正确.
对 D, 直线垂直于 x 轴时不可以用方程 y kx b表示.
故选 C
5.【答案】A
【解析】
由中点坐标公式可得 M(2,4),N(3,2),再由两点式可得直线 MN 的方程为 = ,即 2x+y-8=0.
故选 A
6.【答案】D
【解析】由 A 2,8 ,C 6,0 ,则 A,C 的中点坐标为D 4,4 ,
则过点 B 将 ABC的面积平分的直线过点 D 4,4 ,
4 0
则所求直线方程为 y (x 4) ,
4 ( 4)
即 x 2y 4 0,
故选 D.
7.【答案】 y x 2
【解析】由光学知识可得反射光线所在的直线过点Q 2,0 和 P 6,4 关于 x 轴的对称点M (6, 4),其
y 0 4 0
直线方程为 ,即 x y 2 0 .
x 2 6 2
故填 y x 2
8.【答案】3x 2y 14 0
【解析】∵ AC 的中点M(2,4),
∴ AC 边上的中线 BM 所在的直线方程为:
y 4 x 2
,
1 4 4 2
整理,得3x 2y 14 0,
故填3x 2y 14 0.
9.【答案】5x 6y 1 0
【解析】因为两条直线 l1: a1x b1y 1 0和 l2 :a2x b2 y 1 0相交于点P 5, 6 ,
所以5a1 6b1 1 0 ,5a2 6b2 1 0 ,
所以点 A a1,b1 , B a2 ,b2 都在直线5x 6y 1 0上,
所以过点 A a1,b1 , B a2 ,b2 的直线方程为: 5x 6y 1 0 .
故填5x 6y 1 0
10.【答案】(1) x y 2 0;(2) x 2y 1 0
【解析】(1)因为 A(1,1) ,B(2,0),
y 0 x 2
由直线的两点式方程可得: AB 边所在直线的方程 ,
1 0 1 2
化简可得 x y 2 0;
(2)由B(2,0),C(4,4),
D(2 4 , 0 4则 BC 中点 ) ,即D(3,2) ,
2 2
y 2 x 3
则 BC 边上中线 AD所在直线的方程为 ,
1 2 1 3
化简可得 x 2y 1 0 .
2.2.3 一般式方程
基础练
一、单选题
1.过点(0,1)且与直线 2x﹣y+1=0 垂直的直线方程是( )
A.x+2y﹣1=0 B.x+2y﹣2=0 C.2x﹣y﹣1=0 D.2x﹣y﹣2=0
2.过点(-1,3)且平行于直线 x-2y+3=0 的直线方程为( )
A.2x+y-1=0 B.x-2y+7=0 C.x-2y-5=0 D.2x+y-5=0
3.直线 x 3 y+1=0的倾斜角是( )
A.30° B.60° C.120° D.150°
4.直线方程 kx-y+2-3k=0 恒过定点( )
A.(3,2) B.(2,3) C.(-3,2) D.(-2,3)
5.设直线5x 3y 15 0在 x 轴上截距为a,在 y 轴上的截距为b ,则( )
A.a 5,b 3 B.a 3,b 5 C.a 3,b 5 D.a 3,b 5
6.已知直线方程为ax by c 0.若ac 0,bc 0,则此直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
7.已知直线 l1 :3x y 2 0, l2 :mx y 1 0 .若 l1//l2 ,则m ________.
8.已知直线 l : x 2y 1 0,点 A a,1 , B 2,3 ,若直线 AB l ,则a的值为__________.
9. k 取任意实数时,直线 2 k 1 x k 6 y k 4 0 恒经过定点 P ,则点 P 的坐标为_________.
三、解答题
10.已知直线 l : 2a b x a b y a b 0 及点P 3,4 .
(1)证明直线 l过某定点,并求该定点的坐标.
(2)当点 P 到直线 l的距离最大时,求直线 l的方程.
参考答案
1.【答案】B
【解析】因为过点(0,1)的直线与直线 2x﹣y+1=0 垂直,
1
所以过点(0,1)的直线的斜率为 k ,
2
所以所求直线为 y 1
1
(x 0),即 x 2y 2 0,
2
故选 B
2.【答案】B
【解析】设直线方程式是:x-2y+c=0
因为直线过点(-1,3)
所以-1-6+c=0,解得 c=7
故所求直线方程是:x-2y+7=0
故选 B
3.【答案】D
1 3
【解析】直线 x 3 y+1=0 的斜率 k ,
3 3
设其倾斜角为 θ(0°≤θ<180°),
tan 3则 ,
3
∴θ=150°
故选 D
4.【答案】A
【解析】因为直线方程 kx-y+2-3k=0,
即为 k x 3 y 2 0
x 3 0
所以 ,
y 2 0
x 3
解得 ,
y 2
所以直线恒过定点(3,2).
故选 A
5.【答案】B
【解析】由直线5x 3y 15 0
令 y 0, x 3
令 x 0, y 5
即a 3,b 5
故选 B
6.【答案】B
c
【解析】令 x 0可得 y 0;
b
令 y 0 c可得 x 0,故直线不经过第二象限,
a
故选 B.
7.【答案】3
【解析】因为直线 l1 :3x y 2 0, l2 :mx y 1 0,且 l1//l2 ,
则3 1 1 m,解得m 3 .
故填3 .
8.【答案】1
1
【解析】因为直线 l : x 2y 1 0的斜率为 k ,
2
又点 A a,1 , B 2,3 ,直线 AB l ,
k k 3 1 1所以 AB 1
,即 1,解得:a 1.2 a 2
故填1
9.【答案】(1,-1)
【解析】直线方程可整理为: 2x y 1 k 2x 6y 4 0
2x y 1 0 x 1
令 ,解得:2x 6y 4 0
,即定点P 的坐标为 1, 1
y 1
故填 1, 1 .
10.【答案】(1)证明见解析,定点坐标为 2,3 (2)5x y 7 0
【解析】(1)直线 l方程可化为:a 2x y 1 b x y 1 0
2x y 1 0
由 ,解得 x 2且 y 3,
x y 1 0
直线恒 l过定点 A,其坐标为 2,3 .
(2)由直线恒 l过定点 A 2,3 ,
当点 P 在直线 l上的射影点恰好是 A时,
即 PA l 时,点 P 到直线 l的距离最大
k 4 3 1PA的斜率 PA 3 2 5
1
直线 l的斜率 k 5kPA
由此可得点 P 到直线 l的距离最大时,
直线 l的方程为 y 3 5 x 2 ,即5x y 7 0.
2.2.3 一般式方程
基础练
一、单选题
1.如果 pr 0,qr 0,那么直线 px qy r 0不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知直线 l1 : xsin 2y 1 0,直线 l2 : x ycos 3 0,若 l1 l2 ,则 tan2 ( )
2 4 2 4
A. B. C. D.
3 3 5 5
3.点 P(2,3)到直线:ax (a 1)y 3 0的距离d 最大时,d 与 a 的值依次为( )
A.3,-3 B.5,2 C.5,1 D.7,1
4.设M x1, y1 , N x2 , y2 为不同的两点,直线 l : ax by c 0,
ax1 by c 1
ax2 by c
,下列命题正确的有
2
( )
①不论 为何值,点 N 都不在直线 l上;
②若 1,则过点M , N 的直线与直线 l平行;
③若 1,则直线 l经过MN 的中点;
④若 1,则点M , N 在直线 l的同侧且直线 l与线段MN 的延长线相交.
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题
5.已知m , n为正数,且直线 x n 2 y 5 0与直线nx my 3 0互相垂直,则m 2n 的最小值
为______.
6.方程 x y 6 x y 3m 0表示两条直线,则m 的取值范围是__________.
三、解答题
7.已知直线方程为 2 m x 2m 1 y 3m 4 0 .
(1)证明:直线恒过定点;
(2)m 为何值时,点Q 3,4 到直线的距离最大,最大值为多少?
(3)若直线分别与 x 轴, y 轴的负半轴交于 A, B 两点,求 AOB面积的最小值及此时直线的方程.
参考答案
1.【答案】C
r
【解析】当 x 0时,qy r 0, qr 0, y 0q
r
当 y 0时, px r 0, pr 0, x 0,
p
直线的横截距和纵截距都是正数,所以直线过第一,二,四象限,不过第三象限.
故选 C
2.【答案】B
【解析】因为 l1⊥l2,所以sin 2cos 0,
所以 tanα=2,
所以 tan 2
2 tan 4 4
.
1 tan2 1 4 3
故选 B.
3.【答案】C
【解析】 直线ax a 1 y 3 0,
即 a x y 3 y 0,
直线ax a 1 y 3 0是过直线 x y 0和3 y 0交点的直线系方程,
x y 0 x 3
由 ,得3 y 0
,
y 3
可得直线ax a 1 y 3 0经过定点Q 3,3 ,
当直线ax a 1 y 3 0与PQ垂直时,
点 P 2,3 到直线ax a 1 y 3 0的距离最大,
d 2的最大值为 PQ 2 3 3 3 2 5,
此时PQ / /x 轴,
可得直线ax a 1 y 3 0斜率不存在,即 a 1.
故选 C.
4.【答案】D
ax1 by1 c
【解析】因为 axax by c 中, 2
by2 c 0,所以点 N 不在直线 l 上,故①正确
2 2
ax1 by1 c 1 y2 y1 a当b≠0时,根据 1得到 ax by c ,化简得
2 2 x
,
2 x1 b
a a
即直线MN 的斜率为 ,又直线 l的斜率为 ,由①可知点 N 不在直线 l上,
b b
得到直线MN 与直线 l平行
当b 0时,可得直线MN 与直线 l的斜率都不存在,也满足平行,故②正确
ax by c x x y y
当 1 1 1时,得到 1 1 2 1 2ax by c ,化简得a b c 02 2 2 2
x1 x2 y1 y2
而线段MN 的中点坐标为 , ,所以直线 l经过MN 的中点,故③正确
2 2
ax by c ax by c
当 1 1 1 1 1时,得到 1ax ,所以
0,
2 by2 c ax2 by2 c
即 ax1 by1 c ax2 by2 c 0,所以点M , N 在直线 l 的同侧
且 ax1 by1 c ax2 by2 c ,可得点M 与点 N 到直线 l 的距离不等,
所以延长线与直线 l相交,故④正确
综上:命题正确的有 4 个
故选 D
5.【答案】9
【解析】 直线 x (n 2)y 5 0与直线nx my 3 0互相垂直,
2 1
n (n 2)m 0, 2m n mn, 1,
n m
m 2n (m 2n)(2 1 )=5 2m 2n 2m 2n 5 2 9,
n m n m n m
当且仅当m n 3时取等号.
故填 9
6.【答案】 0,3
【解析】令 t x y 0,则关于 t 的二次方程 t2 6t 3m 0在 t 0, 上有两个不等的实根,
令 f t t2 6t 3m ,则二次函数 f t 在 t 0, 有两个不同的零点,
36 12m 0
所以, f 0 3m 0 ,解得0 m 3 .
因此,实数m 的取值范围是 0,3 .
故填 0,3 .
4
7.【答案】(1)证明见解析(2)m ;2 13 (3)最小值为4;此时直线的方程2x y 4 07
【解析】(1)证明:直线方程为 2 m x 2m 1 y 3m 4 0,可化为
2x y 4 x 2y 3 0 x 1 m x 2y 3 0 ,对任意m 都成立,所以 ,解得 ,所以
2x y 4 0
y 2
直线恒过定点 1, 2 ;
(2)解:点Q 3,4 到直线的距离最大,
可知点Q 与定点P 1, 2 的连线的距离就是所求最大值,
3 1 2
4 2 3
即 4 2 2 2 13 . kPQ ,3 1 2
2 m x 2m 1 y 3m 4 0 2的斜率为 ,
3
2 2 m
可得
4
,解得m .
3 2m 1 7
(3)解:若直线分别与 x 轴, y 轴的负半轴交于 A, B 两点,直线方程为 y 2 k x 1 ,k 0,
2
则 A 1,0
,B 0,k 2 ,
k
S 1 2△AOB 1 k 2
1 2 2 k 2 k
2 k 2
1 k 2 2 2 2 4,
k k 2 k 2
当且仅当k 2时取等号,面积的最小值为4 .
此时直线的方程2x y 4 0 .
2.3.1~2.3.2 直线的交点坐标、两点间的距离公式
基础练
一、单选题
1.已知直线 x 2与直线 y 2x 1交于点 P,则点 P 的坐标为( )
A.(1,5) B.(2,3) C.(3,1) D.(0,0)
2.直线 y x 5与直线 y x 1的交点坐标是( )
A. 1, 2 B. 2,3 C. 3,2 D. 2,1
3.若三条直线2x 3y 8 0, x y 1 0与直线 x ky 0交于一点,则 k ( )
A.-2 B.2 C 1. D 1.
2 2
4.点 A在 x 轴上,点 B 在 y 轴上,线段 AB 的中点M 的坐标是 3,4 ,则 AB 的长为( )
A.5 B.6 C.8 D.10
5.已知点 P a, 2 ,Q 2, 3 ,M 1,1 ,且 PQ PM ,则a的值是()
9 9
A. 2 B.2 C. D.2 2
6.直线2x 3y k 0和 x ky 12 0的交点在 y 轴上,则 k 的值为( )
A.-24 B.6 C. 6 D.-6
二、填空题
7.已知点 A 2,1 ,点B 5, 1 ,则 AB ________.
8.已知直线 l1 : 3x 2y 5 0与直线 l2 : 4x ay 11 0,且 l1 l2 ,则直线 l1与直线 l2 的交点坐标是
______.
x, y 4x my m 29.若关于 的二元一次方程组 有无穷多组解,则m ______.
mx y m 0
三、解答题
3
10.已知直线 l1 的方程为x 2y 4 0,若 l2 在 x 轴上的截距为 ,且 l1 l2 .2
(1)求直线 l1 和 l2 的交点坐标;
(2)已知直线 l3经过 l1 与 l2 的交点,且在 y 轴上截距是在 x 轴上的截距的 2 倍,求 l3的方程.
参考答案
1.【答案】B
【解析】联立直线 x 2与直线 y 2x 1的方程,
容易得 x 2, y 3,
故点 P 的坐标为 2,3 .
故选 B.
2.【答案】B
y x 5 x 2
【解析】联立两直线的方程 ,解得y x 1
,因此,两直线的交点坐标是 2,3 .
y 3
故选 B.
3.【答案】C
【解析】两方程联立可得交点坐标为:( 1, 2),代入第三条直线方程: 1 2 = 0,
解得: = 1.2
故选 C.
4.【答案】D
【解析】设 A x,0 ,B 0,y
因为 AB 的中点M 的坐标是 3,4 ,
所以由中点坐标公式得 x 6,y 8,
所以点 A 6,0 ,B 0,8
则由两点间的距离公式得 | AB | (0 6)2 (8 0)2 100 10 .
故选D .
5.【答案】C
【解析】因为点 P a, 2 ,Q 2, 3 ,M 1,1 ,且 PQ PM ,所以
2 2
9
a 2 2 3 a 1
2 2 1 2 .解得a .2
故选 C.
6.【答案】C
【解析】因为两条直线2x 3y k 0和 x ky 12 0的交点在 y 轴上,
所以设交点为 (0,b),
3b k 0
所以 ,消去b ,可得k 6.
kb 12 0
故选C .
7.【答案】 13
【解析】点 A(2,1),B(5,﹣1),则|AB| 2 5 2 (1 1)2 13.
故填 13 .
2, 18.【答案】
2
【解析】因为 l1 l2 ,所以3 4 2a 0,所以a 6.
3x 2y 5 0,
x 2,
联立 解得 ,
4x 6y 11 0,
y 1 , 2
l l 故直线 1与直线 2 的交点坐标是 2,
1
.
2
2, 1 故填 2
9.【答案】 2
4x my m 2 0
【解析】依题意二元一次方程组 有无穷多组解,即两个方程对应的直线重合,由
mx y m 0
4 1 m m解得m 2或m 2 .
4x 2y 0 2x y 0
当m 2 时,二元一次方程组为 ,两直线不重合,故m 2 不符合
2x y 2 0 2x y 2 0
题意.
4x 2y 4 0 2x y 2 0
当m 2时,二元一次方程组为 ,两直线重合,符合题意.
2x y 2 0
2x y 2 0
综上所述,m 的值为 2 .
故填 2
1
10.【答案】(1) 2,1 ;(2) y x或2x y 5 0
2
k 1
【解析】(1)∵l l1⊥l2,∴ 2 1 2 .
2
3
∴直线 l2的方程为:y﹣0=2(x ),化为:y=2x﹣3.
2
x 2y 4 0 x 2
联立 ,解得 .
2x y 3 0
y 1
∴直线 l1和 l2的交点坐标为(2,1).
1
(2)当直线 l3经过原点时,可得方程:y x.
2
当直线 l3不经过过原点时,设在 x轴上截距为 a≠0,则在 y 轴上的截距的 2a 倍,
x y 2 1 5
其方程为: 1,把交点坐标(2,1)代入可得: 1,解得 a .
a 2a a 2a 2
可得方程:2x+y=5.
综上可得直线 l3的方程为:x﹣2y=0,2x+y﹣5=0.
2.3.3~2.3.4 点到直线的距离、两条平行线间的距离
基础练
一、单选题
1.点(1,-1)到直线 x-y+1=0 的距离是( )
1 3
A B C 2 D 3 2. . . .
2 2 2 2
2.已知点(a,2) (a>0)到直线 l: x-y+3=0 的距离为 1, 则 a 的值为( )
A. 2 B.2- 2 C. 2 -1 D. 2 +1
3.已知点 A 的坐标为(-4,4),直线 l 的方程为 x+y-2=0,则点 A 关于 l 的对称点 A'的坐标为( )
2
A. , 4
B. 2,6 C. 2,4 D. 1,6
3
4.点 M(4,m)关于点 N(n, - 3)的对称点为 P(6,-9)则( )
A.m=-3,n=10 B.m=3,n=10 C.m=-3, n=5 D.m =3, n = 5
5.点 A cos ,sin 到直线3x 4y 4 0距离的最大值为( )
1 4 9
A. B. C.1 D.
5 5 5
6.点 A(1,3)关于直线 y=kx+b 对称的点是 B(–2,1),则直线 y=kx+b 在 x 轴上的截距是( )
3 5 6 5
A. B. C. D.
2 4 5 6
二、填空题
7.点 P 1,2 到直线 l : y 3x的距离为______.
8.点 ( 1,1) 关于直线 x y 1 0的对称点是______.
9.点 P(m,6)到直线3x 4y 2 0的距离不大于 4,则m 的取值范围是________.
三、解答题
10.在平面直角坐标系中,已知直线 l :ax 3y 2 0,若直线 l 在 x 轴上的截距为 2 ,
(1)求实数 a的值,并写出直线 l的斜截式方程;
(2)求出点M (3,1)到直线 l的距离.
参考答案
1.【答案】D
【解析】由题意得点(1,-1)不在直线上,
1 ( 1) 1
1 -1 d 3 2所以点( , )到直线的距离为 .
1 1 2
故选 D.
2.【答案】C
| a 2 3 |
【解析】由点到直线 l 的距离公式得:d 1,解得: a 1 2 ,又a 0,故2 a 2 1
,
故选 C
3.【答案】B
【解析】设点 A( 4,4)关于直线 x y 2 0的对称点 A 的坐标为 (a,b),
b 4
1 a 4
则由 ,求得a 2,b 6,故点 A ( 2,6),
a 4 b 4 2 0
2 2
故选 B.
4.【答案】D
【解析】
4 6 m 9
因为点 M,P 关于点 N 对称,所以由中点坐标公式可知n 5, 3 , m 3 .
2 2
故选 D
5.【答案】D
3cos 4sin 4【解析】点 A cos ,sin 到直线3x 4y 4 0距离d ,
32 42
5sin 4
化简得d ,
5
其中 满足 tan
3
,
4
当 sin 1时d 取得最大值,
即 d 9 .
5
故选 D.
6.【答案】D
3-1 k=-1
{1+2 3 5【解析】由题意知 ,解得 k1 =- ,
b= ,
2 k 2 4= - +b
2
3 5 5
∴直线方程为 y=- x+ ,其在 x 轴上的截距为 .
2 4 6
故选 D
7 10.【答案】
2
【解析】由题可知: l : y 3x,则 l :3x y 0
3 1 2 10
所以点P 1,2 到该直线的距离为d
32 1 2 2
10
故填
2
8.【答案】 2, 2
【解析】设点 M(﹣1,1)关于直线 l:x﹣y﹣1=0 对称的点 N 的坐标(x,y)
x 1 y 1
则 MN 中点的坐标为( , ),
2 2
y 1 x 1 y 1
利用对称的性质得:KMN= =﹣1,且 ﹣ ﹣1=0,
x 1 2 2
解得:x=2,y=﹣2,
∴点 N 的坐标(2,﹣2),
故填(2,﹣2).
2, 46 9.【答案】 3
3m 4 6 2 46
【解析】依题意可知, 4 2 m
32 4 2
,解得 .
3
故填 2,
46
.
3
1 2
10.【答案】(1)a=1; y x 10;(2)
3 3 5
【解析】(1)因为直线 l在 x 轴上的截距为-2,
所以直线经过点(-2,0),
代入直线方程得-2a+2=0,解得 a=1,
所以直线 l的方程为 x-3y+2=0,
所以直线 l的斜截式方程为 y
1
x 2 .
3 3
(2)点 M(3,1)到直线 l的距离,
3 3 2 10
所以d .
12 ( 3)2 5
2.3.3~2.3.4 点到直线的距离、两条平行线间的距离
基础练
一、单选题
1.若两条平行直线 l1 : x 2y m 0 m 0 与 l2 : 2x ny 6 0之间的距离是2 5 ,则m n ( )
A.3 B. 17 C.2 D.3或 17
2.若直线 l与直线 y ax b(a 0)关于直线 y x 对称,则直线 l的方程是( )
y x x x b x bA. b B. y b C. y D. y
a a a a a a
3.在等腰直角三角形 ABC 中,AB AC 2,点 P 是边 AB 上异于 A、B 的一点,光线从点 P 出发,经BC 、
CA反射后又回到点 P(如图所示),若光线QR 经过 ABC的重心,则 AP ( )
1 2 4
A.1 B. C. D.
2 3 3
4.将一张画了直角坐标系(两坐标轴单位长度相同)的纸折叠一次,使点 2,0 与点 2,4 重合,则与点
5,8 重合的点是( )
A. 6,7 B. 7,6 C. 5, 4 D. 4, 5
二、填空题
5.直线ax 2y 6 0与直线 x (a 1)y a2 1 0 平行,则两直线间的距离为______.
6.已知定点 A 到动直线 l:2mx 1 m2 y 4m 2 0(m R)的距离为一常数,则定点 A 的坐标为
________.
三、解答题
7.设集合 A { l |直线与 y 2x直线相交且以交点的横坐标为斜率}.
(1)点 ( 2,0)到 A中哪条直线距离最小;
(2)设 P( 2,a),点 P 到 A中直线距离的最小值设为d(a),求d(a).
参考答案
1.【答案】A
【解析】由题意直线 l1 : x 2y m 0 m 0 与 l2 : 2x ny 6 0平行,
则两条直线的斜率相等,即n 4,
2m 6
又直线间的距离为2 5 ,即 2 5 ,解得m 7 ,
4 16
所以m n 3 .
故选 A
2.【答案】C
【解析】在直线 y ax b(a 0)上任取一点 P x0 , y0 ,设关于直线 y x 的对称点为Q x, y ,
y y0
1
x x x0 y
所以 0 ,解得 ,
y y0 x x 0
y0 x
2 2
代入 y ax b,
得: x ay b,
x b
所以直线 l的方程是 y .
a a
故选 C
3.【答案】C
【解析】建立如图所示的直角坐标系:
可得B(2,0),C(0,2),故直线 BC 的方程为 x y 2,
(0 2 0 , 0 0 2) (2 2ABC的重心为 ,即 , )
3 3 3 3
设 P(a, 0) ,其中0 a 2,
a x y 0
2
P BC P (x, y) 2 2则点 关于直线 的对称点 1 ,满足 ,
y 0 1 1
x a
x 2
解得 ,即P1(2, 2 a) ,P 关于 y轴的对称点P2 ( a,0),
y 2 a
由光的反射原理可知 P1,Q,R,P2四点共线,
2 a 0 2 a
y 2 a直线 QR 的斜率为 k 2 a 2 a ,故直线 QR 的方程为 (x a) ,2 a
2 2
由于直线 QR 过 ABC的重心 ( , ),代入化简可得3a23 3 2a 0
,
解得a
2 2
,或a 0(舍去),故P( ,0)
2
,故 AP
3 3 3
故选 C
4.【答案】A
【解析】由已知得折线为点 2,0 和 2,4 的垂直平分线,
两点 2,0 和 2,4 连线段的中点为 0,2 4 0,斜率为 1,
2 2
∴其垂直平分线的斜率为 1,垂直平分线方程为 y=x+2,
设点 5,8 关于直线 y x 2的对称点为P x0 , y0 ,
y0 8 x 5
0 2
2 2 x0 6
则 y 8 ,解得 , 0 1 y0 7
x0 5
故选 A.
5 6 5.【答案】
5
【解析】直线ax 2y 6 0与直线 x (a 1)y a2 1 0 平行,
则 a(a 1) 2 0,即a2 a 2 0,
解得a 2或 1.
当a 2时,两直线重合,
故a 1,两直线方程可化为: x 2y 6 0与 x 2y 0
| 6 | 6 5
所以两平行线间的距离 d
1 22 5
6 5
故填
5
6.【答案】 2,1
2ma 1 m2 b 4m 2
【解析】设定点 A 为 a,b ,所以点 A到直线 l 的距离d
2m 2
2
1 m2
无论m R, d 为定值,所以令m 0可得,d b 2 ,令m 1可得,d a 3 ,
令m 1可得,d a 1 ,由 a 3 a 1 可得,a 2,即有b 1或b 3.
2ma 1 m2 b 4m 2 1 m2
当定点 A 为 2,1 时,d 1
2 2 2 1 m
2 ,符合题意;
2m 1 m
2ma 1 m2 b 4m 2 1 3m2
当定点 A 为 2,3 时,d 2 1 m2 ,显然d 的值随m 的变化而变化, 2m 2 1 m2
不符题意,舍去.
综上可知,动直线 l是以 2,1 为圆心,半径为1的圆的切线系,所以定点 A 为 2,1 .
故填 2,1 .
2 a 1, a 2
7.【答案】(1)到 y 0距离最小;(2)d (a) a, 0 a 2
0, a 0
2
【解析】(1)设交点为 (k,2k),则直线 l的方程为 y 2k k(x k),即 kx y k 2k 0.
2k k 2 2k
( 2,0) l d k 2 1 1点 到直线 的距离 关于 k 2 单调递增,所以,当 k 0时,
k 2 1 k 2 1
距离最小为 0,此时直线 l的方程为 y 0.
2k a k 2 2k k 2 a (a 1)2
(2)因为d (a) k 2 1 2 2(a 1) ,k 2 1 k 2 1 k 1
2
因为设 t k2 1 1,d (a) f t t (a 1) 2(a 1) ,所以
t
2 d (a) 2 a 1 2(a 1) 2 a 1, a 2当 (a 1) 1,即a 2或 a 0时, ;
0, a 0
当 (a 1)2 1即0 a 2时, f t 在 1, 上单调递增,d (a) f 1 | a | a.
2 a 1, a 2
综上,d (a) a, 0 a 2.
0, a 0
2.4.1 圆的标准方程
基础练
一、单选题
1.圆心为 3,1 ,半径为 5的圆的标准方程是( )
A. x 3 2 y 1 2 5 B x 3 2 2. y 1 25
C. x 3 2 y 1 2 5 D. x 3 2 y 1 2 25
2.已知圆的一条直径的端点分别是 A 0,0 , B 2,4 ,则此圆的方程是( )
A. x 1 2 y 2 2 5 B x 1 2. y 2 2 25
C 2. x 5 2 y2 5 D. x 5 y2 25
3.圆心为 1, 2 ,且与 x轴相切的圆的标准方程为( )
A. x 1 2 y+2 2 2 B x 2 2. 1 y 2 4
C. x 1 2 y 2 2 2 D. x 1 2 y 2 2 4
4.以P 2,3 为圆心,且圆心到 y 轴的距离为半径的圆的方程是( )
A. (x 2)2 (y 3)2 4 B. (x 2)2 (y 3)2 4
C. (x 2)2 (y 3)2 9 D. (x 2)2 (y 3)2 9
5 2.已知圆C 与圆 x 1 y2 1关于直线 y x对称,则圆C 的方程为( )
A. x 1 2 y2 2 B x2. y2 2
C x2. y 1 2 1 D. x2 y 1 2 1
6.若圆C 的半径为 1,圆心在第一象限,且与直线4x 3y 0和 x 轴相切,则该圆的标准方程是( )
2
A (x 2)2 (y 1)2 1 B (x 3)2 y 7 . . 1
3
2
C. (x 1)2 (y 3)2 1 D x 3 . (y 1)
2 1
2
二、填空题
7.圆 C 的圆心为点 8, 3 ,且经过点 A 5,1 ,则圆 C 的方程为________.
8 2.圆 x 1 y2 1的圆心到直线 x 3y 1 0的距离为________.
9.经过点 1,0 、 0,2 且圆心在直线 y 2x上的圆的方程是________.
三、解答题
10.已知圆C 过点O 0,0 , A 6,0 , B 0,8 .
(1)求圆C 的方程;
(2)若 P 为圆C 上的动点,求 PAB面积的最大值.
参考答案
1.【答案】D
【解析】∵所求圆的圆心为 3,1 ,半径为 5,
∴所求圆的标准方程为: x 3 2 y 1 2 25,
故选 D.
2.【答案】A
【解析】 直径两端点为 0,0 , 2,4 圆心坐标为 1, 2
圆的半径 r 1 0 2 2 0 2 5 ,
2 2圆的方程为: x 1 y 2 5 .
故选 A.
3.【答案】B
【解析】因为圆心为 1, 2 ,圆与 x轴相切,
所以圆的半径为 2,
2 2
所以圆的标准方程为 x 1 y 2 4,
故选 B
4.【答案】B
【解析】圆心P 2,3 到 y 轴的距离为 2 2,所以圆的半径为 2,
2 2 2
故圆的方程为 (x 2) (y 3) 2 4 .
故选 B.
5.【答案】C
【解析】由题意,圆心为 0, 1 ,半径 r 1 2,则圆的方程为 x y 1 2 1,
故选 C.
6.【答案】A
【解析】设圆心坐标为(a,b)(a>0,b>0),
4a 3b
由圆与直线 4x-3y=0 相切,可得圆心到直线的距离 d= r 1,化简得:|4a-3b|=5①,
5
又圆与 x 轴相切,可得|b|=r=1,解得 b=1 或 b=-1(舍去),
1
把 b=1 代入①得:4a-3=5 或 4a-3=-5,解得 a=2 或 a=-
2
(舍去),∴圆心坐标为(2,1),
则圆的标准方程为:(x-2)2+(y-1)2=1.
故选 A
7.【答案】 x 8 2 y 3 2 25
【解析】由于圆 C 的圆心为点 8, 3 ,且经过点 A 5,1 ,
圆的半径为 r ,则 r2 8 5 2 3 2 1 25 ,
2
所以圆的方程为 x 8 y 3 2 25,
故填 x 8 2 y 3 2 25 .
8.【答案】1
【解析】圆 x 1 2 y2 1的圆心坐标为 1,0 ,
x 1 2所以圆 y2 1的圆心到直线 x 3y 1 0的距离为:
1 1 3 0 1
d 1
2 ,
12 3
故填 1
9 1
2
5
.【答案】 x y 1
2
2 4
2 2
【解析】设圆的方程为 x a y b r2,
因为圆心 a,b 在直线 y 2x上,得b 2a,
2 2 2
所以可得圆的方程为 x a y 2a r ,
因为圆经过点 1,0 、 0,2 ,
1
1 a
2 0 2a 2 r2 a 2
所以 ,解得 ,
0 a
2 2 2a 2 r2
r
5
2
2
1 5
因此,所求圆的方程为 x y 1
2 ,
2 4
x 1
2
y 1 2 5故填 。
2 4
10 2 2.【答案】(1) x 3 y 4 25 .(2)25.
【解析】(1)由平面几何知识可知,所求圆心为 3,4 ,半径 r 5,
∴圆C 的方程为 x 3 2 y 4 2 25 .
(2) AB 的方程为4x 3y 24 0,
∵ AB 过圆心, AB 10 .
当 P 到直线的距离为 5 时, PAB面积最大,
S 1此时 PAB 10 5 25 .2
2.4.2 圆的一般方程
基础练
一、单选题
1.圆 x2 y2 2x 4y 4 0的圆心是( )
A. 1, 2 B. 2, 4 C. 1,2 D. 2,4
2.已知m 是实常数,若方程 x2 y2 2x 4y m 0 表示的曲线是圆,则m 的取值范围为( )
A. , 20 B. ,5 C. 5, D. 20,
3 x2.圆 y2 4x 6y 9 0的圆心到直线ax y 1 0的距离为 2,则a ( )
4 3
A. B. C. 2 D.23 4
4.已知圆 x2+y2+2x﹣4y﹣8=0 的圆心在直线 3x+y﹣a=0,则实数 a 的值为( )
A.﹣1 B.1 C.3 D.﹣3
5 ax2 by2.若 cxy 2ax 4by a3 0 表示面积为 的圆的方程,则实数a的值为( )
A.2 B. 2 C.1 D. 1
6.圆C : x2 y2 x 6y 3 0 上有两点 A,B 关于直线 kx y 4 0对称,则 k=( )
A.2 B 3 3. C. D.不存在
2 2
二、填空题
7.已知点 A(-4,-5),B(6,-1),则以线段 AB 为直径的圆的一般方程为____.
8 2 2.在平面直角坐标系中,圆的方程为 x y 2x 6y 1 0 ,该圆的周长为__________.
3
9.点 (1, )在圆 x2 y2 2y m2 m 1 0外,则实数m 的取值范围是__________
2
三、解答题
10.已知方程x2 y2 2mx 4y 2m2 3m 0表示一个圆.
(1)求实数m 的取值范围;
(2)求半径 R 的最大值.
参考答案
1.【答案】A
【解析】圆 x2 y2 2x 4y 4 0的标准方程为 x 1 2 2 y 2 1,圆心的坐标为 1, 2 ,
故选 A.
2.【答案】B
【解析】由于方程 x2 y2 2x 4y m 0表示的曲线为圆,则22 42 4m 0,解得m 5 .
因此,实数m 的取值范围是 ,5 .
故选 B.
3.【答案】B
2
【解析】圆的标准方程是 (x 2) (y 3)2 4 ,圆心为 (2,3) ,
2a 3 1
∴ 2
3
,解得a .
a2 1 4
故选 B.
4.【答案】A
【解析】根据题意,圆 x2+y2+2x﹣4y﹣8=0的圆心为(﹣1,2),
若圆 x2+y2+2x﹣4y﹣8=0 的圆心在直线 3x+y﹣a=0 上,则有 3×(﹣1)+2﹣a=0,
解得:a=﹣1;
故选 A.
5.【答案】B
2 2
【解析】方程ax by cxy 2ax 4by a3 0 表示圆,且圆的半径为1,
可得a(x 1)2 b(y 2)2 cxy a 4b a3,
a b 0
可得 c 0 ,解得a 2,经检验,均符合题意.
a 4b a
3
1
a
故选 B.
6.【答案】A
1
【解析】由题意得直线 kx y 4 0
经过圆心C ,3
k
,所以 3 4 0 ,解得 k 2,
2 2
故选 A
7.【答案】 x2 y2 2x 6y 19 0
【解析】因为点 A(-4,-5),B(6,-1)
所以圆心为: 1, 3 ABr 100 16, 29
2 2
所以圆的标准方程为: x 1 2 y 3 2 29
2 2
所以圆的一般方程为: x y 2x 6y 19 0
x2故填 y2 2x 6y 19 0
8.【答案】6
2 2
【解析】由题设可得圆的标准方程为: x 1 y 3 9,
所以圆的半径为R 3,故周长为2 R 6 .
故填6 .
9.【答案】 ( 1
1
, ) (
3 ,2)
2 2
【解析】因为方程 x2 y2 2y m2 m 1 0表示圆,
所以 ( 2)2 4(m2 m 1) 0 ,
得m2 m 2 0,解得 1 m 2.
因为点 (1,
3)在圆 x2 y2 2y m2 m 1 0外,
2
12 (3)2 2 3 m2所以 m 1 0 ,
2 2
1 3
即 4m2 4m 3 0 ,解得m 或m .
2 2
综上,实数m 的取值范围是 ( 1 1, ) (3 ,2) .
2 2
故填 ( 1
1) (3, , 2) .
2 2
10.【答案】(1) 1,4 5;(2) .
2
1 2 2【解析】( ) x m y 2 m2 3m 4 0 1 m 4 ,即实数m 的取值范围是 1,4 ;
3 2 25 25 3 5
(2)R2 m2 3m 4 m
≤ ,当且仅当m 时,半径R 取得最大值 .
2 4 4 2 2
2.5.1 直线与圆的位置关系
基础练
一、单选题
1.直线 y x 2与圆 x2 y2 4 有( )个公共点.
A.0 B.1 C.2 D.3
2.圆 x2 y2 4x 2y 2 0截 x 轴所得弦的长度等于( )
A.2 2 B.2 3 C.4 2 D.2
3.若直线 y 3x b x2与圆 y2 1相切,则b ( )
A 2 3. B. 2 C. 2 D. 5
3
4.已知直线 l :3x 4y m 0被圆C : x2 y2 2x 2y 6 0 截得的弦长为 2 7 ,则m 的值为( )
A.4 或-6 B.-4 或 6 C.4 或 6 D.-4 或-6
5 2 2.已知圆 (x 2) ( y 1) 12 上恰有三个点到直线 l : kx y 0 距离等于 3 ,则直线 l 的斜率为( )
A.2 6 B. 2 6 C. 6 2 D. 6 2
6 2.圆C : x y2 2x 4y 3 0 被直线 l : a x y 1 a 0截得的弦长的最小值为( )
A.1 B.2 C. 2 D. 3
二、填空题
7 2 2.过点M (1, 3) 作圆O : x y 4的切线方程是__________.
8.直线 y=2﹣x x2 y2与圆 4x 5 0 交于 A,B 两点,则|AB|=_____.
9 2 2.过点P(1,1) 作圆 x y 2x 1 0的切线,切点为 A ,则 PA ________.
三、解答题
10.已知圆心为 C(4,3)的圆经过原点 O.
(1)求圆 C 的方程;
(2)设直线 3x﹣4y+15=0 与圆 C 交于 A,B 两点,求△ABC的面积.
参考答案
1.【答案】C
【解析】圆 x2 y2 4 的圆心为坐标原点O 0,0 ,半径 r 2 ,
直线 y x 2的方程化为一般式为: x y 2 0 ,
0 0 2
圆心O到直线 y x 2的距离d 2 r ,
12 12
∴直线 y x 2 2 2与圆 x y 4相交,∴有 2 个公共点,
故选 C.
2.【答案】A
x2 y2【解析】在圆方程 4x 2y 2 0中令 y 0,
得 x2 4x 2 0 x 4 8 2 2
2
因此弦长为| 2 2 ( 2 2) | 2 2
故选 A
3.【答案】C
【解析】由题得圆的圆心坐标为(0,0),
|b |
所以 1, b 2 .
3 1
故选 C
4.【答案】A
2
【解析】圆C 的标准方程为: x 1 y 1 2 8,
故圆心C 到直线 l的距离为d 8 27 1,
3 4 m
所以 1,故m 6或m 4 ,
9 16
故选 A.
5.【答案】A
| 2k 1|
【解析】由题意,圆心到直线 l的距离等于半径的一半,所以 32 ,解得k 2 6 ,k 1
故选 A.
6.【答案】B
【解析】直线 l : a x y 1 a 0可化为 l : a(x 1) (y 1) 0 ,故直线 l恒过点P 1,1 .
圆C : x2 y2 2x 4y 3 0的圆心为C(1,2) ,半径为 2 当直线 l 垂直于直线PC 时,截得的弦
长最短,此时弦长d 2 2 1 2 .
故选 B
7.【答案】 x 3y 4 0
【解析】因为点M 1, 3 2 2 1 3在圆O : x y 4上,所以切点为M 1, 3 ,切线斜率k kOM 3
3
所以由点斜式写方程得 y x 1 3 即 x 3y 4 0
3
故填 x 3y 4 0
8.【答案】2.
2 2 2
【解析】根据题意,圆 x y 4x 5 0 ,即 x 2 y2 9,其圆心为 2,0 ,半径 r 3,
2 2
圆心到直线 y 2 x的距离d 2 2 ,
1 1
则弦长 AB 2 r2 d 2 2 9 8 2 .
故填2 .
9.【答案】 3
2 2
【解析】由题得 (x 1) y 2,所以圆C 的圆心为 ( 1,0) ,半径为 2 .
所以 | PC | (1 1)2 12 5 ,
2 2
所以 | PA | 5 2 3 .
故填 3
10.【答案】(1)(x﹣4)2+(y﹣3)2=25.(2)12
【解析】(1)圆 C 的半径为 OC 32 42 5,
从而圆 C 的方程为(x﹣4)2+(y﹣3)2=25;
(2)作 CD⊥AB 于 D,则 CD 平分线段 AB,
在直角三角形 ADC中,由点到直线的距离公式,得|CD|=3,
所以 AD AC |2 CD |2 4,
所以|AB|=2|AD|=8,
1
所以△ABC 的面积S AB CD 12.
2
2.5.2 圆与圆的位置关系
基础练
一、单选题
1.圆 (x 3)2 (y 2)2 4与圆 (x 7)2 (y 1)2 36的位置关系是( )
A.相切 B.内含 C.相离 D.相交
2.圆 x2 y2 1和圆 x2 y2 6y 5 0的位置关系是( )
A.内含 B.内切 C.外切 D.外离
3.圆 C1:x2+y2=16与圆 C2:(x-3)2+(y-4)2=9 的公共弦的长为( )
12 16 24 32
A. B. C. D.
5 5 5 5
4 2.圆C1 : x y
2 2x 2y 2 0与C2 : x
2 y2 4x 2y 1 0的公切线有且仅有( )
A.1条 B.2条 C.3条 D.4条
5 C x2 y2 4x 6y 12 0 C x 4 2 y 5 2.若圆 1 : 与圆 2 : m 有且仅有 3 条公切线,则实数 m
的值为( )
A.4 B.25 C.5 D.16
6.若圆C1 : x
2 y2 4 2 2与圆C2 : x y 6x 8y m 0外切,则实数m ( )
A. 24 B. 16 C.24 D.16
二、填空题
7 x2 y2 x 0 x2 y2.圆 与圆 2y 0的公共弦所在的直线方程为___________.
8 O 2 2 2 2.若⊙ 1 : x y 5与⊙O2 : (x m) y 20(m R) 相交于 A、B 两点,且两圆在点 A 处的切线互
相垂直,则线段 AB 的长度是 .
9 2 2 2 2.圆C1 : x m y 2 9与圆C2 : x 1 y m 4内切,则m 的值为______.
三、解答题
10.已知两圆C1 : (x 1)
2 (y 1)2 4 C : x2 y2和 2 4ax 2y 4a
2 0 .
(1)把圆C2 化成标准方程;
(2)试求当 a为何值时,两圆C1 和C2 相切.
参考答案
1.【答案】D
【解析】两圆的圆心分别为: A(3, 2),B(7,1),
半径分别为: r 2, R 6,
两圆心距为: | AB | (7 3)2 (1 2)2 5
R r | AB| R r,
所以,两圆相交,
故选 D。
2.【答案】C
2 2 2 2
【解析】∵圆 x y 6y 5 0的标准方程为: x (y 3) 4,
表示以 (0,3)为圆心,半径为 2的圆,
∴两圆圆心距为3,正好等于半径之和,
∴两圆相外切,
故选C .
3.【答案】C
【解析】两圆方程相减得公共弦方程为3x 4y 16 0 ,圆心C1 0,0 ,到公共弦的距离为
16
d 16
2
, 16 24所以所求弦长为 2 42 .32 42 5 5 5
故选 C
4.【答案】B
【解析】圆C1 的标准方程为 x 1 2 y 1 2 4 2,圆C2 的标准方程为 x 2 y 1 2 4,
两圆心分别为C1 1, 1 、C2 2,1 ,半径分别为 r1 r2 2,
C1C2 11 r1 r2 4,两圆相交,因此,两圆有2条公切线,
故选 B.
5.【答案】B
2
【解析】依题意,圆C1 : x 2 y 3 2 25,
由题得C1 与C2 外切,
则 C1C2 r1 r2 ,
故 2 4 2 3 5 2 5 m ,
解得m 25,
故选 B.
6.【答案】D
【解析】圆C1 的圆心为 0,0 ,半径为2,圆C2 的圆心为 3,4 ,半径为 25 m .
两个圆的圆心距为 32 42 5 .
由于两个圆外切,所以 2 25 m 5,解得m 16 .
故选 D
7.【答案】 x 2y 0
【解析】由题:圆 x2 y2 x 0 2 2与圆 x y 2y 0的标准方程为:
1 2 2
x
y
2 1 和 x2 y 1 1,
2 4
5 1 5 3
圆心距为 , ,
2 2 2 2
所以两圆相交,
2 2 2 2
所以公共弦所在直线方程即: x y x x y 2y 0,
即 x 2y 0 .
故填 x 2y 0
8.【答案】4
1 AB 1
【解析】依题意得OO1= 5 20 =5,且△OO1A是直角三角形,S△OO1A= · ·OO1= ·OA·AO1,
2 2 2
2 OA AO 2 5 2 5
因此 AB= 1= =4.
OO1 5
故填 4
9.【答案】 2或 1
【解析】圆C1 的圆心为 m, 2 ,半径为 r1 3,
圆C2 的圆心为 1,m ,半径为 r2 2,
2
所以两圆的圆心距d m 1 m 2 2 ,
m 1 2 m 2 2又因为两圆内切,有 1,
解得m 2或m 1.
故填 2或 1.
10 2 2.【答案】(1)C2 : (x 2a) (y 1) 1;(2)a 0或 1时内切;a 1或 2 时外切.
2 2
【解析】(1)圆C2 的标准方程为:C2 : (x 2a) (y 1) 1;
(2 2)圆C1 : (x 1) (y 1)
2 4的圆心C1 : ( 1,1),半径R1 2,
圆C2 : (x 2a)
2 (y 1)2 1的圆心C2 : (2a,1),半径R2 1,
当两圆外切时: 1 2a 1+2 3,解得 a 1或 2 ;
当两圆内切时: 1 2a 2 1 1,a 0或 1.
2.5.3 直线与圆的综合
基础练
一、单选题
1.已知圆C : x2 2x y2 0 ,则圆心C 到直线 x 3的距离等于( )
A.1 B.2 C.3 D.4
2.已知直线 l : x 3y 0与圆C : x2 (y 1)2 1相交于O, A两点,O为坐标原点,则 COA的面积为
( )
A 3 B 3. . C. 3 D.2 3
4 2
3.已知点 P(2,1)在圆 C:x2+y2+ax–2y+b=0 上,点 P 关于直线 x+y–1=0 的对称点也在圆 C 上,则圆 C
的圆心坐标为( )
A.(0,1) B.(1,0) C.(2,1) D.(1,2)
4 y x 1 x2 y2.垂直于直线 且与圆 4 相切于第三象限的直线方程是( )
A. x y 2 2 0 B. x y 2 0
C. x y 2 0 D. x y 2 2 0
5 2 2.直线 x y 2 0截圆 x y 4 所得劣弧所对圆心角为( )
2
A. B. C. D.
6 3 2 3
6.已知圆C 的圆心在曲线 y 3 x 0 上,直线 l过 3,3 且与直线4x 3y 5 0垂直,则与直线 l 相
x
切的面积最小的圆C 的方程为( )
2 2
A. x 2 2 y 3 3
3 B. x 2
2 y
9
2 2
2 2
C 3 3 3 . x y 2 3 D. x y 2
2 9
2 2
二、填空题
7 2 2.过圆 x y 36内的一点 A 2,4 引此圆的弦MN ,则 MN 的最小值为______.
8.已知直线 l与圆 x2 y2 2y 0相交于 A, B
1 1
两点,且线段 AB 的中点 P 坐标为 , ,则直线 l 的方
2 2
程为__________.
9.经过原点并且与直线 x y 2 0相切于点 2,0 的圆的标准方程是__________.
三、解答题
10.已知圆C : (x 3)2 (y 4)2 4和直线 l : kx y 4k 3 0
(1)求证:不论 k 取什么值,直线 l和圆 C 总相交;
(2)求直线 l被圆 C 截得的最短弦长及此时的直线方程.
参考答案
1.【答案】D
【解析】由题 x 2 1 y2 1 ,则圆心(-1,0),则圆心C 到直线x 3的距离等 3-(-1)=4
故选 D
2.【答案】A
【解析】由题意直线 l,圆C 均过原点,通过图形观察可知 COA为等腰三角形,且CO CA r 1,
OCA 120 1 1 3 3,所以 S 2 . COA CO CA sin OCA 1 2 2 2 4
故选 A.
3.【答案】A
【解析】依题意有:如图所示,根据图形的对称性可知:点P 2,1 关于直线 x y 1 0对称的点是
点Q 3 2a b 00, 1 ,分别将P,Q 两点的坐标代入圆的方程得 ,解得a 0,b 3,而圆心坐
b 3 0
a ,1 标为 ,故圆心坐标为 0,1 .
2
故选 A
4.【答案】A
【解析】设所求的直线为 l,
直线 l垂直于直线 y x 1,可得直线 l的斜率为k 1,
设直线 l方程为 y x b,即 x y b 0,
2 2
又直线 l与圆 x y 4 相切,
圆心O(0,0) 到直线 l的距离 d
| b |
2,
2
解得b 2 2
当b 2 2 时,可得切点坐标 2, 2 ,切点在第三象限;
当b 2 2 时,可得切点坐标 2, 2 ,切点在第一象限;
直线 l x2 y2与圆 1的切点在第三象限,
取b 2 2 ,此时的直线方程为 x y 2 2 0.
故选 A.
5.【答案】D
【解析】由题意有,该圆圆心为 (0,0) ,半径为 2,
2
圆心到直线的距离d 1,
2
∴弦长 l 2 22 12 =2 3 ,
22 22 cos (2 3)
2 1
由余弦定理得圆心角 的余弦值 ,
2 2 2 2
2
∴圆心角 = .
3
故选 D.
6.【答案】B
3
【解析】依题意,设圆C 的圆心坐标为 a, a
a 0 .设直线 l:3x 4y b 0,将 3,3 代入可
知,b 3,故直线 l的方程为3x 4y 3 0;
因为直线 l与故圆C 相切,
12 12
故圆C 3a 3 2 3a 3 12的半径 a a ,当且仅当3a ,即a 2时,等号成立,此R 3 a
5 5
3 22
时圆C 的方程为 x 2 y 9 .
2
故选 B.
7.【答案】8
【解析】如图,
由平面几何知识得,当过点 A的弦MN 垂直于OA时,MN 最短,
所以 MN 2 36
min 22 42 8.
故填 8.
8.【答案】 x y 0
2
【解析】把圆的方程化为标准方程得: x2 y 1 1,
可得圆心C(0,1), 直线CP的斜率为 1,
直线 AB 的斜率为 1,
1 1
则直线 AB 的方程为: y (x ),即 x y 0.
2 2
故填 x y 0.
9 x 1 2 y 1 2.【答案】 2
【解析】设圆心坐标 (a,b),则a2
b
b2 r2, (a 2)2 b2 r 2 , 1,根据这三个方程组可以a 2
2 2
计算得:a 1,b 1, r 2 ,所以所求方程为: (x 1) (y 1) 2 ,
2 2
故填 x 1 y 1 2
10.【答案】(1)详见解析;(2)2 2 , x y 1 0 .
【解析】(1)由直线 l的方程 y 3 k x 4 可得直线 l 恒通过点 4,3 ,而点 4,3 在圆C 的内部,
故得到不论k 取什么值,直线 l和圆 C 总相交;
(2)设定点为 A 4,3 k 4 3,因为 CA 1,求出直线 l的斜率,即可写出直线 l 的方程,3 4
求出圆心到直线 l的距离d ,即可求出弦长。
解析:(1)证明:由直线 l的方程可得, y 3 k x 4 ,则直线 l恒通过点
4,3 ,把 4,3 2 2代入圆的C 方程,得 4 3 3 4 2 4 ,
所以点 4,3 在圆C 的内部,又因为直线 l恒过点 4,3 ,
所以直线 l与圆C 总相交.
(2)设定点为 A 4,3 ,由题可知当直线 l与CA直线垂直时,直线 l被圆C 截得的弦长最短,
4 3
因为 kCA 1,所以直线 l的斜率为k 13 4
所以直线 l的方程为 y 3 x 4,即 x y 1 0
3 4 1设圆心C 3,4 到直线 l距离为d ,则d 2
2
2
所以直线 l被圆C 截得最短的弦长为2 4 2 2 2 .
2.6 章末复习课
基础练
一、单选题
l 0 2
1.若直线 的倾斜角 满足 ,且 ,则其斜率
3 k 满足( )2
A. 3 k 0 B. k 3
C k 0 k 3 D k 0 k 3. 或 . 或
3
2.点 1,1 在圆 x2 y 1 2 1的( )
A.圆上 B.圆内 C.圆外 D.无法判定
3.设直线 l的方程为2x 4y 3 0,直线m 的方程为 x 2y 6 0,则直线 l与m 的距离为( )
A 3 5 B 3 5 C 9 5 D 9 5. . . .
10 5 10 5
4 x 2 2.圆 y2 4 x 2 2 y 3 2与圆 25的位置关系为( )
A.内切 B.外切 C.相交 D.相离
5 2 2.已知定点B 3,0 ,点 A在圆 (x 1) y 4上运动,则线段 AB 的中点M 的轨迹方程是( )
A (x 1)2. y2 1 B. (x 2)2 y2 4
C 2 2. (x 1) y 1 D. (x 2)2 y2 4
6.以 1,m 为圆心,且与两条直线 2x y 4 0,2x y 6 0都相切的圆的标准方程为( )
A. x 1 2 y 9 2 5 B x 1 2. y 11 2 25
C. x 2 2 1 y 1 5 D 2. x 1 y 9 2 25
二、填空题
7.直线3x 2y k 0在两坐标轴上的截距之和为2,则实数 k ______.
8.若圆 (x 1)2 (y 4)2 5的圆心到直线 x y a 0 2的距离为 ,则a 的值为_________.
2
9.已知圆C : (x 1)2 (y 2)2 5,过圆C 外一点P 3,4 作圆的两条切线PA,PB切点分别为 A,B ,
则直线 AB 的方程为_______.
三、解答题
10 C : x2 y2 2x 8 C : x2 4ax y2 2y 3 4a2.已知圆 1 ,圆 2
(1)若 a 1,求两圆心连线C1C2 的中垂线的一般式方程;
(2)若 a 1,且动点 P 满足PC1 2PC2 ,求 P 点轨迹方程;
(3)若两圆相切,求 a的值.
参考答案
1.【答案】C
k tan 0 2
【解析】斜率 ,因为 ,且 ,3 2
故 tan 0或 tan 3 ,即 k 0或 k 3 ,
故选 C.
2.【答案】A
【解析】将点 1,1 的坐标代入圆 x2 y 1 2 1的方程即12 1 1 2 1,∴点 1,1 在圆 x2 y 1 2 1
上,
故选 A.
3.【答案】C
3 12
【解析】直线m 的方程可化为2x 4y 12 0,因此,直线 l与m 9 5的距离为d .
22 42 10
故选 C.
4.【答案】C
2
【解析】根据题意,圆(x 2) y2 4的圆心为 ( 2,0) ,半径 r1 2 ;
圆 x 2 2 y 3 2 25的圆心为 (2,3) ,半径 r2 5 ;
两圆的圆心距d 42 32 5,有5 2 d 5 2,
则两圆相交;
故选 C.
5.【答案】C
xA 3 yA xA 2x 3
【解析】设M x, y ,则 A xA, yA 满足 , x, y .故 .故 A 2x 3,2y . 2 2 yA 2y
2 2
又点 A在圆 (x 1) y 4上.故 (2x 3 1)2 2y 2 4 x 1 2 y2 1 .
故选 C
6.【答案】C
2 m 4 2 m 6
【解析】设圆的半径为 r ,则 r ,
5 5
m 1
则 ,
r 5
2
即圆的标准方程为 x 1 y 1 2 5,
故选 C.
7.【答案】12
x 0 y k【解析】令 ,则 ;令 y 0,则 x k ,
2 3
k k
故
2,解得k 12 .2 3
故填12 .
8.【答案】4或 2
3 a
【解析】圆 (x 1)2 2 (y 4)2 5的圆心为 1, 4 ,它到直线 x y a 0的距离为 ,
2 2
故a 2或a 4 .
故填 4 或 2.
9.【答案】2x 6y 5 0.
【解析】设 A x1, y1 ,B x2 , y2 ,则切线PA的方程为
x1 1 x 1 y1 2 y 2 5,因为点P 3,4 在切线PA上,所以切线PA的方程为
2x1 6y1 5,即2x1 6y1 5 0①,同理,切线PB的方程为2x2 6y2 5 0②,由①②得,
直线 AB 的方程为2x 6y 5 0.
故填2x 6y 5 0.
10.【答案】(1)3x y 2 0;(2) x 5 2 1 y 2 2 20 3 a 2 6 1;( ) 或a
2 2
【解析】(1)当 a 1时,
圆C1 : x
2 y2 2x 8 x 1 2,即为 y2 9,圆心为C1 1,0 ,
C : x2 4x y2 2y 3 4 C : x 2 2 y 1 2圆 2 ,即 2 4,圆心为C2 2, 1 ,
1 1 0 1 1
则两圆心的中点坐标为 , , kC C , 2 2 1 2 1 2 3
1 1
两圆心连线C1C2 的中垂线为: y 3 x ,
2 2
整理得一般式为:3x y 2 0;
(2)设P x, y ,C1 1,0 ,C2 2, 1 ,
PC1 2PC
2
2,即PC1 2PC
2
2 ,
x 1 2 y2 2 x 2 2 y 1 2 ,
2 2
整理得 P 点轨迹方程为 x 5 y 2 20 ;
(3)圆C1 : x
2 y2 2x 8,即为 x 1 2 y2 9,圆心为C1 1,0 ,
C : x2圆 2 4ax y
2 2y 3 4a2 ,即C2 : x 2a
2 y 1 2 4,圆心为C2 2a, 1 ,
若两圆相切,
2 2 6 1
当两圆外切时: 2a 1 12 3 2,解得a ;
2
当两圆内切时: 2a 1 2 12 3 2,解得a
1
,
2
a 2 6 1
1
综合得:若两圆相切, 或 a .
2 2
基础练
一、单选题
1.直线 3x y 1 0的倾斜角是( )
3 2 5
A. B. C. D.
4 3 4 6
2.已知直线 l经过点 A 1,3 ,B 2, 5 ,则直线 l的斜率为( )
8 8A. B. C.2 D.3 23
3.如果过 P(-2,m),Q(m,4)两点的直线的斜率为 1,那么 m 的值是( )
A.1 B.4 C.1 或 3 D.1或 4
4.已知直线 l经过两点O(0,0), A(1, 3),直线m的倾斜角是直线 l的倾斜角的两倍,则直线m的斜率是( )
A 3 3. 3 B. C. D. 3
3 3
5.过点 2,1 且倾斜角比直线 y x 1 的倾斜角小 的直线方程是( )
4
A. x 2 B. y 1 C. x 1 D. y 2
6.下列各直线中,与直线2x y 3 0相交的是( )
A.2ax ay 6 0 a 0 B. y 2x
C.2x y 3 0 D.2x y 5 0
二、填空题
7.若直线 x 1的倾斜角为 ,则 的弧度数是________.
8.已知点 A 1,3 ,点B 3,9 ,则直线 AB 的斜率为__________.
9.已知线段MN 两端点的坐标分别为 M(-1,2)和 N(2,3),若直线 kx-y+k-2=0 与线段MN 有交点,
则实数 k的取值范围是________.
三、解答题
10.(1)求经过下列两点的直线的斜率,并判断其倾斜角是锐角、直角还是钝角.
① 3,5 , 0,2 ;
② 4,4 , 4,5 ;
③ m, 2 3m 3 , 2m 1,3 3m m 1 .
(2)已知点 A 3, 5 , B 1,3 ,C 5,11 .求证:A,B,C 三点共线.
参考答案
1.【答案】B
【解析】设直线的倾斜角为 ,
因为直线方程为 3x y 1 0,所以直线的斜率为 3 ,
所以 tan 3 ,
因为 [0, ),所以 2 ,
3
故选 B
2.【答案】A
5 3 8
【解析】因为直线 l经过点 A 1,3 , B 2, 5 ,所以直线 l 的斜率为 .
2 1 3
故选 A.
3.【答案】A
【解析】由题意,过过 P(-2,m),Q(m,4)两点的直线的斜率为 1,
4 m
根据直线的斜率公式,可得 1,解得
m ( 2) m 1
.
故选 A.
4.【答案】A
k 3 0
2
【解析】依题意 OA 3,所以直线 l的倾斜角为 ,所以直线m 的倾斜角为 ,所以直1 0 3 3
线m 的斜率为 tan 2 3 .
3
故选 A
5.【答案】A
3
【解析】直线 y x 1的斜率为 1,倾斜角为 ,故比它的倾斜角小 的直线的倾斜角为 ,
4 4 2
再根据此直线过点 2,1 ,故要求的直线的方程为 x 2 .
故选 A.
6.【答案】C
【解析】 直线2x y 3 0的斜率为:2
与直线2x y 3 0相交的直线的方程的斜率不等于 2
A, B ,D的斜率均为 2,C 的斜率为 2
故选 C.
7.【答案】
2
【解析】因为直线 x 1垂直 x轴,
所以其倾斜角弧度数为 .
2
故填 .
2
3
8.【答案】
2
【解析】因为 A 1,3 , B 3,9
3 9 3
则 kAB 1 3 2
3
故填
2
5
9.【答案】 ,+ 3
【解析】直线 kx-y+k-2=0过定点 P(-1,-2).
3 2 5
此时 MP 平行于 y轴, kNP ,2 1 3
5
所以 k ≥ .
3
5
故填 ,+ . 3
10.【答案】(1)①钝角,②直角,③锐角;(2)证明见解析
2 5
【解析】(1)① k 1 00 3 ,倾斜角为钝角;
②k不存在,倾斜角为直角;
3 3m 2 3m 3
k 3m 3③ 3 0,倾斜角为锐角.
2m 1 m m 1
3 5 11 3
(2)证明: kAB 2 , k 2 ,且 AB,BC 都经过点 B,1 3 BC 5 1
A,B,C 三点共线.
2.1.2 两条直线平行与垂直的判定
基础练
一、单选题
1.直线ax y 1 0与直线2x 3y 2 0平行,则实数 a的值为( )
2 3
A. B. 1 C. D.6
3 2
2.“a=1”是“直线 x+y=0 和直线 x-ay=0 互相垂直”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.若直线 a,b 的斜率分别为方程 x2 4x 1 0的两个根,则 a与 b的位置关系为( )
A.互相平行 B.互相重合 C.互相垂直 D.无法确定
4.若直线ax 3y 1 0与 x y 4 0互相垂直,则 a 的值为( )
1 2
A.1 B. C. D. 3
2 3
5.已知直线 l1 : x 2ay 1 0,与 l2 : 2a 1 x ay 1 0 平行,则a的值是( )
1 1 1
A.0 或 1 B.1 或 C.0 或 D.
4 4 4
6.已知直线mx 4y 2 0与2x 5y n 0互相垂直,垂足为P 1, p ,则m n p的值是( )
A.24 B.20 C.0 D. 4
二、填空题
7.若直线 l1 : ax 3y 5 0与 l2 : x 2y 1 0互相垂直,则实数a的值为________.
8.已知直线 l :mx y 1 0,若直线 l 与直线 x my 1 0平行,则 m 的值为__________.
9.已知点 A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线 AB 与直线 CD平行,则 m 的值为_______;
三、解答题
10.已知直线 l1 : x my 6 0, l2 : m 2 x 3y 2m 0 .
(1)若 l1 l2 ,求m 的值;
(2)若 l1 / /l2 ,求m 的值.
参考答案
1.【答案】A
【解析】因为直线ax y 1 0与直线2x 3y 2 0平行,
所以 a 2 2 a ,
3 3
故选 A.
2.【答案】C
【解析】直线 x y 0和直线 x ay 0互相垂直的充要条件是1 ( a) 1 1 0,即 a 1,
故选 C
3.【答案】C
【解析】由题意 kakb 1,∴两直线垂直.
故选 C.
4.【答案】D
【解析】∵直线ax 3y 1 0与直线 x y 4 0互相垂直,
∴斜率之积等于 1,
a
∴ 1 1,得a 3 .
3
故选 D.
5.【答案】C
【解析】由题意得:1 ( a) (2a 1) 2a 0, a 0 1或a ,
4
故选 C.
6.【答案】B
【解析】∵两直线互相垂直,∴k1·k2=-1,
m 2
∴- · =-1,∴m=10.又∵垂足为(1,p),
4 5
∴代入直线 10x+4y-2=0 得 p=-2,
将(1,-2)代入直线 2x-5y+n=0得 n=-12,
∴m-n+p=20.
故选 B.
7.【答案】 6
【解析】两直线 l1 : ax 3y 5 0与 l2 : x 2y 1 0互相垂直.
所以a 1 3 2 0,解得a 6
故填 6
8.【答案】 1
【解析】因为直线 l与直线 x my 1 0平行,
m ( m) 1 1 m 1
所以有 m 1 .
m ( 1) 1 1
m 1
故填 1
9.【答案】0或 1
【解析】当m 0时,直线 AB 方程为 x 0,直线CD方程为 x 1,两直线平行,
k m 4 3 m 1 2 0 2 m 1 2当m 0时, AB ,k2m m m CD
,由 得m 1,此时直线 AB 方
m 1 1 m m m
程为 y 3 2(x 1),即 y 2x 1,直线CD方程为 y 2(x 1) ,即 y 2x 2 ,两直线平行.
故填 0 或 1.
10.【答案】(1)m 1 ;(2)m 1
2
【解析】(1)∵直线 l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,
由 l1⊥l2 ,可得 1×(m﹣2)+m×3=0 1,解得m .
2
(2)由题意可知 m 不等于 0,
由 l1∥l m 2 3 2m2 可得 ,解得 m=﹣1.
1 m 8
2.2.1 点斜式方程
基础练
一、单选题
2
1.过点 3,2 ,斜率是 的直线方程是( )
3
2
A. y x 2 4 B. y x 2 C.2x 3y 0 D.3x 2y 0
3 3
2.方程 y y0 k x x0 ( )
A.可以表示任何直线 B.不能表示过原点的直线
C.不能表示与 y 轴垂直的直线 D.不能表示与 x 轴垂直的直线
3.过点 2,0 且与直线 y 2x 5垂直的直线 l 的方程是( )
A. y 2x 4 B. y 2x 4 1C. y x 1 1D. y x 1
2 2
4.已知直线 l过点 2,0 ,且与直线 y 2x 1平行,则直线 l 的方程为( )
A. y 2x 4 B. y 2x 4 C. y 2x 4 D. y 2x 4
5.已知 A 5,2 , B 1,4 ,则 AB 的垂直平分线方程为( )
A. x 3y 7 0 B.3x y 3 0 C.3x y 7 0 D.3x y 7 0
6.过点 A(1,2)且与原点距离最大的直线方程是( )
A. x 2y 5 0 B.2x y 4 0 C. x 3y 7 0 D.3x y 5 0
二、填空题
7.直线 l过点M 1, 2 ,倾斜角为60 .则直线 l的斜截式方程为______________.
8.已知 ABC的三个顶点 A(2,3),B(4, 1),C( 2, 9),若点D, E 分别是边 AB, AC 的中点,则线段DE
所在直线的点斜式方程是________________.
9.已知点 P1(2,3)、P2(-4,5)和 A(-1,2),则过点 A 且与点 P1、P2距离相等的直线方程为______.
三、解答题
10.求适合下列条件的直线方程:
1 A 1, 3 y 3( )经过点 ,倾斜角等于直线 x 的倾斜角的2倍;
3
(2)经过点B 3,4 ,且与两坐标轴围成一个等腰直角三角形.
参考答案
1.【答案】C
【解析】∵直线过点 3,2 2且斜率为 ,
3
由直线方程的点斜式得: y 2 2 (x 3) ,
3
整理得:2x 3y 0 .
故选 C.
2.【答案】D
【解析】因为直线的点斜式方程不能表示斜率不存在的直线,
所以 y y0 k x x0 不能表示与 x 轴垂直的直线,
故选 D。
3.【答案】D
【解析】因为所求直线与直线 y 2x 5垂直,
1
所以其斜率为 k ,
2
又所求直线过点 2,0 ,
1 1
因此,所求直线方程为: y x 2 ,即 y x 1 .
2 2
故选 D.
4.【答案】C
【解析】 直线 l与直线 y 2x 1平行,
直线 l的斜率与 y 2x 1的斜率相等,即直线 l的斜率:k 2;
又 直线 l过点 2,0 ,
则由点斜式可知直线方程为 y 0 2 x 2
整理可得: y 2x 4
故选 C.
5.【答案】B
【解析】设线段 AB 的中点坐标为 x, y ,
5 1
则 x 2, y
2 4
3,中点坐标为 2,3 ,
2 2
k 4 2 1直线 AB 的斜率 ,
1 5 3
AB垂直平分线的斜率为 3,
则 AB 的垂直平分线方程为 y 3 3 x 2 ,
化简得3x y 3 0,
故选 B.
6.【答案】A
【解析】由题知:过点 A(1,2)且与原点距离最大的直线为过点 A(1,2)且与OA垂直的直线.
k 2 y 2 1因为 OA ,故所求直线为 x 1 ,即 x 2y 5 0 .2
故选 A
7.【答案】 y 3x 3 2
【解析】 直线 l的倾斜角为60 , 直线 l的斜率k tan 60 3 ,
又因为直线 l过点M 1, 2 ,所以直线 l的方程为 y 2 3 x 1 ,即 y 3x 3 2,
所以直线 l的斜截式方程为 y 3x 3 2 .
故填 y 3x 3 2 .
4
8.【答案】 y 3 (x 0) y 1 4 或者 (x 3)
3 3
【解析】因为 A(2,3),B(4, 1),C( 2, 9),点D, E 分别是边 AB, AC 的中点,
所以D(3,1),E(0, 3),
1 ( 3) 4
直线DE 的斜率为 ,
3 0 3
4 4
所以线段DE 所在直线的点斜式方程是 y 3 (x 0) 或者 y 1 (x 3) .
3 3
故填 y 3
4
(x 0) 4或者 y 1 (x 3)
3 3
9.【答案】x+3y﹣5=0或 x=﹣1.
【解析】①当直线与点 P1,P2的连线平行时,
3 5 1
由直线 P1P2的斜率 k ,
2 4 3
1
所以所求直线方程为 y﹣2 (x+1),
3
即 x+3y﹣5=0;
②当直线过线段 P1P2的中点时,
因为线段 P1P2的中点为(﹣1,4),
所以直线方程为 x=﹣1.
∴所求直线方程为 x+3y﹣5=0或 x=﹣1,
故答填 x+3y﹣5=0 或 x=﹣1.
10.【答案】(1) 3x y 3 3 0(2) x y 1 0或 x y 7 0.
2 tan
【解析】(1)已知 tan = 3 , k tan 2 2 33 1 tan
直线方程为 y 3 3(x 1)化简得 3x y 3 3 0
(2)由题意可知,所求直线的斜率为 .
又过点 3,4 ,由点斜式得 y 4 x 3 ,
所求直线的方程为 x y 1 0或 x y 7 0.
2.2.2 两点式方程
基础练
一、单选题
1.过 1, 2 , 5,3 的直线方程是( )
y 2 x 1 y 2 x 1 y 1 x 3 x 2 y 3
A. B. C. D.
5 1 3 1 3 2 5 1 5 1 5 3 5 2 2 3
2.已知三角形三个顶点 A 5,0 , B 3, 3 ,C 0,2 ,则 BC 边上中线所在直线方程是( )
A. x 13y 5 0 B. x 13y 5 0 C. x 13y 5 0 D. x 13y 0
3.经过点 A(2,5) , B( 3,6) 的直线在 x 轴上的截距为( )
A.2 B. 3 C. 27 D.27
4.下列命题中,真命题的序号是( )
A.经过定点P0 x0 , y0 直线都可以用方程 y y0 k x x0
x y
B.不经过原点的直线都可以用方程 1表示;
a b
C.过任意不同两点 P1 x1, y1 、P2 x2 , y2 的直线都可以用方程 y y1 x2 x1 x x2 y2 y1
D.经过 A 0,b 的直线都可以用方程 y kx b表示
5.已知 ABC的三个顶点为 A(1,2),B(3,6) ,C(5,2),M 为 AB 的中点,N 为 AC 的中点,则中位线MN
所在直线方程为( )
A.2x y 8 0 B.2x y 8 0
C.2x y 12 0 D.2x y 12 0
6.已知△ABC的三个顶点分别为 A 2,8 ,B 4,0 ,C 6,0 ,则过点 B 将 ABC的面积平分的直线方
程为( )
A.2x y 4 0 B. x 2y 4 0
C.2x y 4 0 D. x 2y 4 0
二、填空题
7.一条光线从点P(6,4)射出,与 x 轴相较于点Q(2,0),经 x 轴反射,则反射光线所在的直线方程为______
8.已知 ABC的三个顶点分别为 A 1,2 , B 4,1 ,C 3,6 ,则 AC 边上的中线BM 所在直线的方程为
______.
9.两条直线 l1:a1x b1y 1 0和 l2 :a2x b2 y 1 0相交于点 P 5, 6 ,则过点 A a1,b1 ,B a2 ,b2
的直线方程为_______
三、解答题
10.已知△ABC的三个顶点 A(1,1) ,B(2,0),C(4,4) .
(1)求 AB 边所在直线的方程;
(2)求BC 边上中线所在直线的方程.
参考答案
1.【答案】B
【解析】因为所求直线过点 1, 2 , 5,3 ,
y 2 3 2 y 2 x 1
所以 ,即 .
x 1 5 1 3 2 5 1
故选 B
2.【答案】C
【解析】 B 3, 3 ,C 0,2 0 3 2 3 3 1, BC 中点的坐标为( , ),即( , ).
2 2 2 2
3 1
则 BC 边上的中线应过 A 5,0 , , 2 2 两点,
y x 5
由两点式得: 0 1 3 5 ,整理,得
x 13y 5 0.
2 2
故选 C.
3.【答案】D
【解析】由两点式得直线方程为=,即 x+5y-27=0,令 y=0 得 x=27.
故选 D.
4.【答案】C
【解析】对 A,当经过定点P0 x0 , y0 直线垂直于 x 轴时不成立.故 A 错误.
x x y对 B, 直线垂直于 轴时不可以用方程 1表示.故 B 错误.
a b
y y
对 C,当直线P1P2 斜率存在时,方程为 y y1
2 1 x x
x x 2 成立
.
2 1
当直线P1P2 斜率不存在时 x1 x2 ,方程为 x x2 成立.故 C 正确.
对 D, 直线垂直于 x 轴时不可以用方程 y kx b表示.
故选 C
5.【答案】A
【解析】
由中点坐标公式可得 M(2,4),N(3,2),再由两点式可得直线 MN 的方程为 = ,即 2x+y-8=0.
故选 A
6.【答案】D
【解析】由 A 2,8 ,C 6,0 ,则 A,C 的中点坐标为D 4,4 ,
则过点 B 将 ABC的面积平分的直线过点 D 4,4 ,
4 0
则所求直线方程为 y (x 4) ,
4 ( 4)
即 x 2y 4 0,
故选 D.
7.【答案】 y x 2
【解析】由光学知识可得反射光线所在的直线过点Q 2,0 和 P 6,4 关于 x 轴的对称点M (6, 4),其
y 0 4 0
直线方程为 ,即 x y 2 0 .
x 2 6 2
故填 y x 2
8.【答案】3x 2y 14 0
【解析】∵ AC 的中点M(2,4),
∴ AC 边上的中线 BM 所在的直线方程为:
y 4 x 2
,
1 4 4 2
整理,得3x 2y 14 0,
故填3x 2y 14 0.
9.【答案】5x 6y 1 0
【解析】因为两条直线 l1: a1x b1y 1 0和 l2 :a2x b2 y 1 0相交于点P 5, 6 ,
所以5a1 6b1 1 0 ,5a2 6b2 1 0 ,
所以点 A a1,b1 , B a2 ,b2 都在直线5x 6y 1 0上,
所以过点 A a1,b1 , B a2 ,b2 的直线方程为: 5x 6y 1 0 .
故填5x 6y 1 0
10.【答案】(1) x y 2 0;(2) x 2y 1 0
【解析】(1)因为 A(1,1) ,B(2,0),
y 0 x 2
由直线的两点式方程可得: AB 边所在直线的方程 ,
1 0 1 2
化简可得 x y 2 0;
(2)由B(2,0),C(4,4),
D(2 4 , 0 4则 BC 中点 ) ,即D(3,2) ,
2 2
y 2 x 3
则 BC 边上中线 AD所在直线的方程为 ,
1 2 1 3
化简可得 x 2y 1 0 .
2.2.3 一般式方程
基础练
一、单选题
1.过点(0,1)且与直线 2x﹣y+1=0 垂直的直线方程是( )
A.x+2y﹣1=0 B.x+2y﹣2=0 C.2x﹣y﹣1=0 D.2x﹣y﹣2=0
2.过点(-1,3)且平行于直线 x-2y+3=0 的直线方程为( )
A.2x+y-1=0 B.x-2y+7=0 C.x-2y-5=0 D.2x+y-5=0
3.直线 x 3 y+1=0的倾斜角是( )
A.30° B.60° C.120° D.150°
4.直线方程 kx-y+2-3k=0 恒过定点( )
A.(3,2) B.(2,3) C.(-3,2) D.(-2,3)
5.设直线5x 3y 15 0在 x 轴上截距为a,在 y 轴上的截距为b ,则( )
A.a 5,b 3 B.a 3,b 5 C.a 3,b 5 D.a 3,b 5
6.已知直线方程为ax by c 0.若ac 0,bc 0,则此直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
7.已知直线 l1 :3x y 2 0, l2 :mx y 1 0 .若 l1//l2 ,则m ________.
8.已知直线 l : x 2y 1 0,点 A a,1 , B 2,3 ,若直线 AB l ,则a的值为__________.
9. k 取任意实数时,直线 2 k 1 x k 6 y k 4 0 恒经过定点 P ,则点 P 的坐标为_________.
三、解答题
10.已知直线 l : 2a b x a b y a b 0 及点P 3,4 .
(1)证明直线 l过某定点,并求该定点的坐标.
(2)当点 P 到直线 l的距离最大时,求直线 l的方程.
参考答案
1.【答案】B
【解析】因为过点(0,1)的直线与直线 2x﹣y+1=0 垂直,
1
所以过点(0,1)的直线的斜率为 k ,
2
所以所求直线为 y 1
1
(x 0),即 x 2y 2 0,
2
故选 B
2.【答案】B
【解析】设直线方程式是:x-2y+c=0
因为直线过点(-1,3)
所以-1-6+c=0,解得 c=7
故所求直线方程是:x-2y+7=0
故选 B
3.【答案】D
1 3
【解析】直线 x 3 y+1=0 的斜率 k ,
3 3
设其倾斜角为 θ(0°≤θ<180°),
tan 3则 ,
3
∴θ=150°
故选 D
4.【答案】A
【解析】因为直线方程 kx-y+2-3k=0,
即为 k x 3 y 2 0
x 3 0
所以 ,
y 2 0
x 3
解得 ,
y 2
所以直线恒过定点(3,2).
故选 A
5.【答案】B
【解析】由直线5x 3y 15 0
令 y 0, x 3
令 x 0, y 5
即a 3,b 5
故选 B
6.【答案】B
c
【解析】令 x 0可得 y 0;
b
令 y 0 c可得 x 0,故直线不经过第二象限,
a
故选 B.
7.【答案】3
【解析】因为直线 l1 :3x y 2 0, l2 :mx y 1 0,且 l1//l2 ,
则3 1 1 m,解得m 3 .
故填3 .
8.【答案】1
1
【解析】因为直线 l : x 2y 1 0的斜率为 k ,
2
又点 A a,1 , B 2,3 ,直线 AB l ,
k k 3 1 1所以 AB 1
,即 1,解得:a 1.2 a 2
故填1
9.【答案】(1,-1)
【解析】直线方程可整理为: 2x y 1 k 2x 6y 4 0
2x y 1 0 x 1
令 ,解得:2x 6y 4 0
,即定点P 的坐标为 1, 1
y 1
故填 1, 1 .
10.【答案】(1)证明见解析,定点坐标为 2,3 (2)5x y 7 0
【解析】(1)直线 l方程可化为:a 2x y 1 b x y 1 0
2x y 1 0
由 ,解得 x 2且 y 3,
x y 1 0
直线恒 l过定点 A,其坐标为 2,3 .
(2)由直线恒 l过定点 A 2,3 ,
当点 P 在直线 l上的射影点恰好是 A时,
即 PA l 时,点 P 到直线 l的距离最大
k 4 3 1PA的斜率 PA 3 2 5
1
直线 l的斜率 k 5kPA
由此可得点 P 到直线 l的距离最大时,
直线 l的方程为 y 3 5 x 2 ,即5x y 7 0.
2.2.3 一般式方程
基础练
一、单选题
1.如果 pr 0,qr 0,那么直线 px qy r 0不通过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知直线 l1 : xsin 2y 1 0,直线 l2 : x ycos 3 0,若 l1 l2 ,则 tan2 ( )
2 4 2 4
A. B. C. D.
3 3 5 5
3.点 P(2,3)到直线:ax (a 1)y 3 0的距离d 最大时,d 与 a 的值依次为( )
A.3,-3 B.5,2 C.5,1 D.7,1
4.设M x1, y1 , N x2 , y2 为不同的两点,直线 l : ax by c 0,
ax1 by c 1
ax2 by c
,下列命题正确的有
2
( )
①不论 为何值,点 N 都不在直线 l上;
②若 1,则过点M , N 的直线与直线 l平行;
③若 1,则直线 l经过MN 的中点;
④若 1,则点M , N 在直线 l的同侧且直线 l与线段MN 的延长线相交.
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题
5.已知m , n为正数,且直线 x n 2 y 5 0与直线nx my 3 0互相垂直,则m 2n 的最小值
为______.
6.方程 x y 6 x y 3m 0表示两条直线,则m 的取值范围是__________.
三、解答题
7.已知直线方程为 2 m x 2m 1 y 3m 4 0 .
(1)证明:直线恒过定点;
(2)m 为何值时,点Q 3,4 到直线的距离最大,最大值为多少?
(3)若直线分别与 x 轴, y 轴的负半轴交于 A, B 两点,求 AOB面积的最小值及此时直线的方程.
参考答案
1.【答案】C
r
【解析】当 x 0时,qy r 0, qr 0, y 0q
r
当 y 0时, px r 0, pr 0, x 0,
p
直线的横截距和纵截距都是正数,所以直线过第一,二,四象限,不过第三象限.
故选 C
2.【答案】B
【解析】因为 l1⊥l2,所以sin 2cos 0,
所以 tanα=2,
所以 tan 2
2 tan 4 4
.
1 tan2 1 4 3
故选 B.
3.【答案】C
【解析】 直线ax a 1 y 3 0,
即 a x y 3 y 0,
直线ax a 1 y 3 0是过直线 x y 0和3 y 0交点的直线系方程,
x y 0 x 3
由 ,得3 y 0
,
y 3
可得直线ax a 1 y 3 0经过定点Q 3,3 ,
当直线ax a 1 y 3 0与PQ垂直时,
点 P 2,3 到直线ax a 1 y 3 0的距离最大,
d 2的最大值为 PQ 2 3 3 3 2 5,
此时PQ / /x 轴,
可得直线ax a 1 y 3 0斜率不存在,即 a 1.
故选 C.
4.【答案】D
ax1 by1 c
【解析】因为 axax by c 中, 2
by2 c 0,所以点 N 不在直线 l 上,故①正确
2 2
ax1 by1 c 1 y2 y1 a当b≠0时,根据 1得到 ax by c ,化简得
2 2 x
,
2 x1 b
a a
即直线MN 的斜率为 ,又直线 l的斜率为 ,由①可知点 N 不在直线 l上,
b b
得到直线MN 与直线 l平行
当b 0时,可得直线MN 与直线 l的斜率都不存在,也满足平行,故②正确
ax by c x x y y
当 1 1 1时,得到 1 1 2 1 2ax by c ,化简得a b c 02 2 2 2
x1 x2 y1 y2
而线段MN 的中点坐标为 , ,所以直线 l经过MN 的中点,故③正确
2 2
ax by c ax by c
当 1 1 1 1 1时,得到 1ax ,所以
0,
2 by2 c ax2 by2 c
即 ax1 by1 c ax2 by2 c 0,所以点M , N 在直线 l 的同侧
且 ax1 by1 c ax2 by2 c ,可得点M 与点 N 到直线 l 的距离不等,
所以延长线与直线 l相交,故④正确
综上:命题正确的有 4 个
故选 D
5.【答案】9
【解析】 直线 x (n 2)y 5 0与直线nx my 3 0互相垂直,
2 1
n (n 2)m 0, 2m n mn, 1,
n m
m 2n (m 2n)(2 1 )=5 2m 2n 2m 2n 5 2 9,
n m n m n m
当且仅当m n 3时取等号.
故填 9
6.【答案】 0,3
【解析】令 t x y 0,则关于 t 的二次方程 t2 6t 3m 0在 t 0, 上有两个不等的实根,
令 f t t2 6t 3m ,则二次函数 f t 在 t 0, 有两个不同的零点,
36 12m 0
所以, f 0 3m 0 ,解得0 m 3 .
因此,实数m 的取值范围是 0,3 .
故填 0,3 .
4
7.【答案】(1)证明见解析(2)m ;2 13 (3)最小值为4;此时直线的方程2x y 4 07
【解析】(1)证明:直线方程为 2 m x 2m 1 y 3m 4 0,可化为
2x y 4 x 2y 3 0 x 1 m x 2y 3 0 ,对任意m 都成立,所以 ,解得 ,所以
2x y 4 0
y 2
直线恒过定点 1, 2 ;
(2)解:点Q 3,4 到直线的距离最大,
可知点Q 与定点P 1, 2 的连线的距离就是所求最大值,
3 1 2
4 2 3
即 4 2 2 2 13 . kPQ ,3 1 2
2 m x 2m 1 y 3m 4 0 2的斜率为 ,
3
2 2 m
可得
4
,解得m .
3 2m 1 7
(3)解:若直线分别与 x 轴, y 轴的负半轴交于 A, B 两点,直线方程为 y 2 k x 1 ,k 0,
2
则 A 1,0
,B 0,k 2 ,
k
S 1 2△AOB 1 k 2
1 2 2 k 2 k
2 k 2
1 k 2 2 2 2 4,
k k 2 k 2
当且仅当k 2时取等号,面积的最小值为4 .
此时直线的方程2x y 4 0 .
2.3.1~2.3.2 直线的交点坐标、两点间的距离公式
基础练
一、单选题
1.已知直线 x 2与直线 y 2x 1交于点 P,则点 P 的坐标为( )
A.(1,5) B.(2,3) C.(3,1) D.(0,0)
2.直线 y x 5与直线 y x 1的交点坐标是( )
A. 1, 2 B. 2,3 C. 3,2 D. 2,1
3.若三条直线2x 3y 8 0, x y 1 0与直线 x ky 0交于一点,则 k ( )
A.-2 B.2 C 1. D 1.
2 2
4.点 A在 x 轴上,点 B 在 y 轴上,线段 AB 的中点M 的坐标是 3,4 ,则 AB 的长为( )
A.5 B.6 C.8 D.10
5.已知点 P a, 2 ,Q 2, 3 ,M 1,1 ,且 PQ PM ,则a的值是()
9 9
A. 2 B.2 C. D.2 2
6.直线2x 3y k 0和 x ky 12 0的交点在 y 轴上,则 k 的值为( )
A.-24 B.6 C. 6 D.-6
二、填空题
7.已知点 A 2,1 ,点B 5, 1 ,则 AB ________.
8.已知直线 l1 : 3x 2y 5 0与直线 l2 : 4x ay 11 0,且 l1 l2 ,则直线 l1与直线 l2 的交点坐标是
______.
x, y 4x my m 29.若关于 的二元一次方程组 有无穷多组解,则m ______.
mx y m 0
三、解答题
3
10.已知直线 l1 的方程为x 2y 4 0,若 l2 在 x 轴上的截距为 ,且 l1 l2 .2
(1)求直线 l1 和 l2 的交点坐标;
(2)已知直线 l3经过 l1 与 l2 的交点,且在 y 轴上截距是在 x 轴上的截距的 2 倍,求 l3的方程.
参考答案
1.【答案】B
【解析】联立直线 x 2与直线 y 2x 1的方程,
容易得 x 2, y 3,
故点 P 的坐标为 2,3 .
故选 B.
2.【答案】B
y x 5 x 2
【解析】联立两直线的方程 ,解得y x 1
,因此,两直线的交点坐标是 2,3 .
y 3
故选 B.
3.【答案】C
【解析】两方程联立可得交点坐标为:( 1, 2),代入第三条直线方程: 1 2 = 0,
解得: = 1.2
故选 C.
4.【答案】D
【解析】设 A x,0 ,B 0,y
因为 AB 的中点M 的坐标是 3,4 ,
所以由中点坐标公式得 x 6,y 8,
所以点 A 6,0 ,B 0,8
则由两点间的距离公式得 | AB | (0 6)2 (8 0)2 100 10 .
故选D .
5.【答案】C
【解析】因为点 P a, 2 ,Q 2, 3 ,M 1,1 ,且 PQ PM ,所以
2 2
9
a 2 2 3 a 1
2 2 1 2 .解得a .2
故选 C.
6.【答案】C
【解析】因为两条直线2x 3y k 0和 x ky 12 0的交点在 y 轴上,
所以设交点为 (0,b),
3b k 0
所以 ,消去b ,可得k 6.
kb 12 0
故选C .
7.【答案】 13
【解析】点 A(2,1),B(5,﹣1),则|AB| 2 5 2 (1 1)2 13.
故填 13 .
2, 18.【答案】
2
【解析】因为 l1 l2 ,所以3 4 2a 0,所以a 6.
3x 2y 5 0,
x 2,
联立 解得 ,
4x 6y 11 0,
y 1 , 2
l l 故直线 1与直线 2 的交点坐标是 2,
1
.
2
2, 1 故填 2
9.【答案】 2
4x my m 2 0
【解析】依题意二元一次方程组 有无穷多组解,即两个方程对应的直线重合,由
mx y m 0
4 1 m m解得m 2或m 2 .
4x 2y 0 2x y 0
当m 2 时,二元一次方程组为 ,两直线不重合,故m 2 不符合
2x y 2 0 2x y 2 0
题意.
4x 2y 4 0 2x y 2 0
当m 2时,二元一次方程组为 ,两直线重合,符合题意.
2x y 2 0
2x y 2 0
综上所述,m 的值为 2 .
故填 2
1
10.【答案】(1) 2,1 ;(2) y x或2x y 5 0
2
k 1
【解析】(1)∵l l1⊥l2,∴ 2 1 2 .
2
3
∴直线 l2的方程为:y﹣0=2(x ),化为:y=2x﹣3.
2
x 2y 4 0 x 2
联立 ,解得 .
2x y 3 0
y 1
∴直线 l1和 l2的交点坐标为(2,1).
1
(2)当直线 l3经过原点时,可得方程:y x.
2
当直线 l3不经过过原点时,设在 x轴上截距为 a≠0,则在 y 轴上的截距的 2a 倍,
x y 2 1 5
其方程为: 1,把交点坐标(2,1)代入可得: 1,解得 a .
a 2a a 2a 2
可得方程:2x+y=5.
综上可得直线 l3的方程为:x﹣2y=0,2x+y﹣5=0.
2.3.3~2.3.4 点到直线的距离、两条平行线间的距离
基础练
一、单选题
1.点(1,-1)到直线 x-y+1=0 的距离是( )
1 3
A B C 2 D 3 2. . . .
2 2 2 2
2.已知点(a,2) (a>0)到直线 l: x-y+3=0 的距离为 1, 则 a 的值为( )
A. 2 B.2- 2 C. 2 -1 D. 2 +1
3.已知点 A 的坐标为(-4,4),直线 l 的方程为 x+y-2=0,则点 A 关于 l 的对称点 A'的坐标为( )
2
A. , 4
B. 2,6 C. 2,4 D. 1,6
3
4.点 M(4,m)关于点 N(n, - 3)的对称点为 P(6,-9)则( )
A.m=-3,n=10 B.m=3,n=10 C.m=-3, n=5 D.m =3, n = 5
5.点 A cos ,sin 到直线3x 4y 4 0距离的最大值为( )
1 4 9
A. B. C.1 D.
5 5 5
6.点 A(1,3)关于直线 y=kx+b 对称的点是 B(–2,1),则直线 y=kx+b 在 x 轴上的截距是( )
3 5 6 5
A. B. C. D.
2 4 5 6
二、填空题
7.点 P 1,2 到直线 l : y 3x的距离为______.
8.点 ( 1,1) 关于直线 x y 1 0的对称点是______.
9.点 P(m,6)到直线3x 4y 2 0的距离不大于 4,则m 的取值范围是________.
三、解答题
10.在平面直角坐标系中,已知直线 l :ax 3y 2 0,若直线 l 在 x 轴上的截距为 2 ,
(1)求实数 a的值,并写出直线 l的斜截式方程;
(2)求出点M (3,1)到直线 l的距离.
参考答案
1.【答案】D
【解析】由题意得点(1,-1)不在直线上,
1 ( 1) 1
1 -1 d 3 2所以点( , )到直线的距离为 .
1 1 2
故选 D.
2.【答案】C
| a 2 3 |
【解析】由点到直线 l 的距离公式得:d 1,解得: a 1 2 ,又a 0,故2 a 2 1
,
故选 C
3.【答案】B
【解析】设点 A( 4,4)关于直线 x y 2 0的对称点 A 的坐标为 (a,b),
b 4
1 a 4
则由 ,求得a 2,b 6,故点 A ( 2,6),
a 4 b 4 2 0
2 2
故选 B.
4.【答案】D
【解析】
4 6 m 9
因为点 M,P 关于点 N 对称,所以由中点坐标公式可知n 5, 3 , m 3 .
2 2
故选 D
5.【答案】D
3cos 4sin 4【解析】点 A cos ,sin 到直线3x 4y 4 0距离d ,
32 42
5sin 4
化简得d ,
5
其中 满足 tan
3
,
4
当 sin 1时d 取得最大值,
即 d 9 .
5
故选 D.
6.【答案】D
3-1 k=-1
{1+2 3 5【解析】由题意知 ,解得 k1 =- ,
b= ,
2 k 2 4= - +b
2
3 5 5
∴直线方程为 y=- x+ ,其在 x 轴上的截距为 .
2 4 6
故选 D
7 10.【答案】
2
【解析】由题可知: l : y 3x,则 l :3x y 0
3 1 2 10
所以点P 1,2 到该直线的距离为d
32 1 2 2
10
故填
2
8.【答案】 2, 2
【解析】设点 M(﹣1,1)关于直线 l:x﹣y﹣1=0 对称的点 N 的坐标(x,y)
x 1 y 1
则 MN 中点的坐标为( , ),
2 2
y 1 x 1 y 1
利用对称的性质得:KMN= =﹣1,且 ﹣ ﹣1=0,
x 1 2 2
解得:x=2,y=﹣2,
∴点 N 的坐标(2,﹣2),
故填(2,﹣2).
2, 46 9.【答案】 3
3m 4 6 2 46
【解析】依题意可知, 4 2 m
32 4 2
,解得 .
3
故填 2,
46
.
3
1 2
10.【答案】(1)a=1; y x 10;(2)
3 3 5
【解析】(1)因为直线 l在 x 轴上的截距为-2,
所以直线经过点(-2,0),
代入直线方程得-2a+2=0,解得 a=1,
所以直线 l的方程为 x-3y+2=0,
所以直线 l的斜截式方程为 y
1
x 2 .
3 3
(2)点 M(3,1)到直线 l的距离,
3 3 2 10
所以d .
12 ( 3)2 5
2.3.3~2.3.4 点到直线的距离、两条平行线间的距离
基础练
一、单选题
1.若两条平行直线 l1 : x 2y m 0 m 0 与 l2 : 2x ny 6 0之间的距离是2 5 ,则m n ( )
A.3 B. 17 C.2 D.3或 17
2.若直线 l与直线 y ax b(a 0)关于直线 y x 对称,则直线 l的方程是( )
y x x x b x bA. b B. y b C. y D. y
a a a a a a
3.在等腰直角三角形 ABC 中,AB AC 2,点 P 是边 AB 上异于 A、B 的一点,光线从点 P 出发,经BC 、
CA反射后又回到点 P(如图所示),若光线QR 经过 ABC的重心,则 AP ( )
1 2 4
A.1 B. C. D.
2 3 3
4.将一张画了直角坐标系(两坐标轴单位长度相同)的纸折叠一次,使点 2,0 与点 2,4 重合,则与点
5,8 重合的点是( )
A. 6,7 B. 7,6 C. 5, 4 D. 4, 5
二、填空题
5.直线ax 2y 6 0与直线 x (a 1)y a2 1 0 平行,则两直线间的距离为______.
6.已知定点 A 到动直线 l:2mx 1 m2 y 4m 2 0(m R)的距离为一常数,则定点 A 的坐标为
________.
三、解答题
7.设集合 A { l |直线与 y 2x直线相交且以交点的横坐标为斜率}.
(1)点 ( 2,0)到 A中哪条直线距离最小;
(2)设 P( 2,a),点 P 到 A中直线距离的最小值设为d(a),求d(a).
参考答案
1.【答案】A
【解析】由题意直线 l1 : x 2y m 0 m 0 与 l2 : 2x ny 6 0平行,
则两条直线的斜率相等,即n 4,
2m 6
又直线间的距离为2 5 ,即 2 5 ,解得m 7 ,
4 16
所以m n 3 .
故选 A
2.【答案】C
【解析】在直线 y ax b(a 0)上任取一点 P x0 , y0 ,设关于直线 y x 的对称点为Q x, y ,
y y0
1
x x x0 y
所以 0 ,解得 ,
y y0 x x 0
y0 x
2 2
代入 y ax b,
得: x ay b,
x b
所以直线 l的方程是 y .
a a
故选 C
3.【答案】C
【解析】建立如图所示的直角坐标系:
可得B(2,0),C(0,2),故直线 BC 的方程为 x y 2,
(0 2 0 , 0 0 2) (2 2ABC的重心为 ,即 , )
3 3 3 3
设 P(a, 0) ,其中0 a 2,
a x y 0
2
P BC P (x, y) 2 2则点 关于直线 的对称点 1 ,满足 ,
y 0 1 1
x a
x 2
解得 ,即P1(2, 2 a) ,P 关于 y轴的对称点P2 ( a,0),
y 2 a
由光的反射原理可知 P1,Q,R,P2四点共线,
2 a 0 2 a
y 2 a直线 QR 的斜率为 k 2 a 2 a ,故直线 QR 的方程为 (x a) ,2 a
2 2
由于直线 QR 过 ABC的重心 ( , ),代入化简可得3a23 3 2a 0
,
解得a
2 2
,或a 0(舍去),故P( ,0)
2
,故 AP
3 3 3
故选 C
4.【答案】A
【解析】由已知得折线为点 2,0 和 2,4 的垂直平分线,
两点 2,0 和 2,4 连线段的中点为 0,2 4 0,斜率为 1,
2 2
∴其垂直平分线的斜率为 1,垂直平分线方程为 y=x+2,
设点 5,8 关于直线 y x 2的对称点为P x0 , y0 ,
y0 8 x 5
0 2
2 2 x0 6
则 y 8 ,解得 , 0 1 y0 7
x0 5
故选 A.
5 6 5.【答案】
5
【解析】直线ax 2y 6 0与直线 x (a 1)y a2 1 0 平行,
则 a(a 1) 2 0,即a2 a 2 0,
解得a 2或 1.
当a 2时,两直线重合,
故a 1,两直线方程可化为: x 2y 6 0与 x 2y 0
| 6 | 6 5
所以两平行线间的距离 d
1 22 5
6 5
故填
5
6.【答案】 2,1
2ma 1 m2 b 4m 2
【解析】设定点 A 为 a,b ,所以点 A到直线 l 的距离d
2m 2
2
1 m2
无论m R, d 为定值,所以令m 0可得,d b 2 ,令m 1可得,d a 3 ,
令m 1可得,d a 1 ,由 a 3 a 1 可得,a 2,即有b 1或b 3.
2ma 1 m2 b 4m 2 1 m2
当定点 A 为 2,1 时,d 1
2 2 2 1 m
2 ,符合题意;
2m 1 m
2ma 1 m2 b 4m 2 1 3m2
当定点 A 为 2,3 时,d 2 1 m2 ,显然d 的值随m 的变化而变化, 2m 2 1 m2
不符题意,舍去.
综上可知,动直线 l是以 2,1 为圆心,半径为1的圆的切线系,所以定点 A 为 2,1 .
故填 2,1 .
2 a 1, a 2
7.【答案】(1)到 y 0距离最小;(2)d (a) a, 0 a 2
0, a 0
2
【解析】(1)设交点为 (k,2k),则直线 l的方程为 y 2k k(x k),即 kx y k 2k 0.
2k k 2 2k
( 2,0) l d k 2 1 1点 到直线 的距离 关于 k 2 单调递增,所以,当 k 0时,
k 2 1 k 2 1
距离最小为 0,此时直线 l的方程为 y 0.
2k a k 2 2k k 2 a (a 1)2
(2)因为d (a) k 2 1 2 2(a 1) ,k 2 1 k 2 1 k 1
2
因为设 t k2 1 1,d (a) f t t (a 1) 2(a 1) ,所以
t
2 d (a) 2 a 1 2(a 1) 2 a 1, a 2当 (a 1) 1,即a 2或 a 0时, ;
0, a 0
当 (a 1)2 1即0 a 2时, f t 在 1, 上单调递增,d (a) f 1 | a | a.
2 a 1, a 2
综上,d (a) a, 0 a 2.
0, a 0
2.4.1 圆的标准方程
基础练
一、单选题
1.圆心为 3,1 ,半径为 5的圆的标准方程是( )
A. x 3 2 y 1 2 5 B x 3 2 2. y 1 25
C. x 3 2 y 1 2 5 D. x 3 2 y 1 2 25
2.已知圆的一条直径的端点分别是 A 0,0 , B 2,4 ,则此圆的方程是( )
A. x 1 2 y 2 2 5 B x 1 2. y 2 2 25
C 2. x 5 2 y2 5 D. x 5 y2 25
3.圆心为 1, 2 ,且与 x轴相切的圆的标准方程为( )
A. x 1 2 y+2 2 2 B x 2 2. 1 y 2 4
C. x 1 2 y 2 2 2 D. x 1 2 y 2 2 4
4.以P 2,3 为圆心,且圆心到 y 轴的距离为半径的圆的方程是( )
A. (x 2)2 (y 3)2 4 B. (x 2)2 (y 3)2 4
C. (x 2)2 (y 3)2 9 D. (x 2)2 (y 3)2 9
5 2.已知圆C 与圆 x 1 y2 1关于直线 y x对称,则圆C 的方程为( )
A. x 1 2 y2 2 B x2. y2 2
C x2. y 1 2 1 D. x2 y 1 2 1
6.若圆C 的半径为 1,圆心在第一象限,且与直线4x 3y 0和 x 轴相切,则该圆的标准方程是( )
2
A (x 2)2 (y 1)2 1 B (x 3)2 y 7 . . 1
3
2
C. (x 1)2 (y 3)2 1 D x 3 . (y 1)
2 1
2
二、填空题
7.圆 C 的圆心为点 8, 3 ,且经过点 A 5,1 ,则圆 C 的方程为________.
8 2.圆 x 1 y2 1的圆心到直线 x 3y 1 0的距离为________.
9.经过点 1,0 、 0,2 且圆心在直线 y 2x上的圆的方程是________.
三、解答题
10.已知圆C 过点O 0,0 , A 6,0 , B 0,8 .
(1)求圆C 的方程;
(2)若 P 为圆C 上的动点,求 PAB面积的最大值.
参考答案
1.【答案】D
【解析】∵所求圆的圆心为 3,1 ,半径为 5,
∴所求圆的标准方程为: x 3 2 y 1 2 25,
故选 D.
2.【答案】A
【解析】 直径两端点为 0,0 , 2,4 圆心坐标为 1, 2
圆的半径 r 1 0 2 2 0 2 5 ,
2 2圆的方程为: x 1 y 2 5 .
故选 A.
3.【答案】B
【解析】因为圆心为 1, 2 ,圆与 x轴相切,
所以圆的半径为 2,
2 2
所以圆的标准方程为 x 1 y 2 4,
故选 B
4.【答案】B
【解析】圆心P 2,3 到 y 轴的距离为 2 2,所以圆的半径为 2,
2 2 2
故圆的方程为 (x 2) (y 3) 2 4 .
故选 B.
5.【答案】C
【解析】由题意,圆心为 0, 1 ,半径 r 1 2,则圆的方程为 x y 1 2 1,
故选 C.
6.【答案】A
【解析】设圆心坐标为(a,b)(a>0,b>0),
4a 3b
由圆与直线 4x-3y=0 相切,可得圆心到直线的距离 d= r 1,化简得:|4a-3b|=5①,
5
又圆与 x 轴相切,可得|b|=r=1,解得 b=1 或 b=-1(舍去),
1
把 b=1 代入①得:4a-3=5 或 4a-3=-5,解得 a=2 或 a=-
2
(舍去),∴圆心坐标为(2,1),
则圆的标准方程为:(x-2)2+(y-1)2=1.
故选 A
7.【答案】 x 8 2 y 3 2 25
【解析】由于圆 C 的圆心为点 8, 3 ,且经过点 A 5,1 ,
圆的半径为 r ,则 r2 8 5 2 3 2 1 25 ,
2
所以圆的方程为 x 8 y 3 2 25,
故填 x 8 2 y 3 2 25 .
8.【答案】1
【解析】圆 x 1 2 y2 1的圆心坐标为 1,0 ,
x 1 2所以圆 y2 1的圆心到直线 x 3y 1 0的距离为:
1 1 3 0 1
d 1
2 ,
12 3
故填 1
9 1
2
5
.【答案】 x y 1
2
2 4
2 2
【解析】设圆的方程为 x a y b r2,
因为圆心 a,b 在直线 y 2x上,得b 2a,
2 2 2
所以可得圆的方程为 x a y 2a r ,
因为圆经过点 1,0 、 0,2 ,
1
1 a
2 0 2a 2 r2 a 2
所以 ,解得 ,
0 a
2 2 2a 2 r2
r
5
2
2
1 5
因此,所求圆的方程为 x y 1
2 ,
2 4
x 1
2
y 1 2 5故填 。
2 4
10 2 2.【答案】(1) x 3 y 4 25 .(2)25.
【解析】(1)由平面几何知识可知,所求圆心为 3,4 ,半径 r 5,
∴圆C 的方程为 x 3 2 y 4 2 25 .
(2) AB 的方程为4x 3y 24 0,
∵ AB 过圆心, AB 10 .
当 P 到直线的距离为 5 时, PAB面积最大,
S 1此时 PAB 10 5 25 .2
2.4.2 圆的一般方程
基础练
一、单选题
1.圆 x2 y2 2x 4y 4 0的圆心是( )
A. 1, 2 B. 2, 4 C. 1,2 D. 2,4
2.已知m 是实常数,若方程 x2 y2 2x 4y m 0 表示的曲线是圆,则m 的取值范围为( )
A. , 20 B. ,5 C. 5, D. 20,
3 x2.圆 y2 4x 6y 9 0的圆心到直线ax y 1 0的距离为 2,则a ( )
4 3
A. B. C. 2 D.23 4
4.已知圆 x2+y2+2x﹣4y﹣8=0 的圆心在直线 3x+y﹣a=0,则实数 a 的值为( )
A.﹣1 B.1 C.3 D.﹣3
5 ax2 by2.若 cxy 2ax 4by a3 0 表示面积为 的圆的方程,则实数a的值为( )
A.2 B. 2 C.1 D. 1
6.圆C : x2 y2 x 6y 3 0 上有两点 A,B 关于直线 kx y 4 0对称,则 k=( )
A.2 B 3 3. C. D.不存在
2 2
二、填空题
7.已知点 A(-4,-5),B(6,-1),则以线段 AB 为直径的圆的一般方程为____.
8 2 2.在平面直角坐标系中,圆的方程为 x y 2x 6y 1 0 ,该圆的周长为__________.
3
9.点 (1, )在圆 x2 y2 2y m2 m 1 0外,则实数m 的取值范围是__________
2
三、解答题
10.已知方程x2 y2 2mx 4y 2m2 3m 0表示一个圆.
(1)求实数m 的取值范围;
(2)求半径 R 的最大值.
参考答案
1.【答案】A
【解析】圆 x2 y2 2x 4y 4 0的标准方程为 x 1 2 2 y 2 1,圆心的坐标为 1, 2 ,
故选 A.
2.【答案】B
【解析】由于方程 x2 y2 2x 4y m 0表示的曲线为圆,则22 42 4m 0,解得m 5 .
因此,实数m 的取值范围是 ,5 .
故选 B.
3.【答案】B
2
【解析】圆的标准方程是 (x 2) (y 3)2 4 ,圆心为 (2,3) ,
2a 3 1
∴ 2
3
,解得a .
a2 1 4
故选 B.
4.【答案】A
【解析】根据题意,圆 x2+y2+2x﹣4y﹣8=0的圆心为(﹣1,2),
若圆 x2+y2+2x﹣4y﹣8=0 的圆心在直线 3x+y﹣a=0 上,则有 3×(﹣1)+2﹣a=0,
解得:a=﹣1;
故选 A.
5.【答案】B
2 2
【解析】方程ax by cxy 2ax 4by a3 0 表示圆,且圆的半径为1,
可得a(x 1)2 b(y 2)2 cxy a 4b a3,
a b 0
可得 c 0 ,解得a 2,经检验,均符合题意.
a 4b a
3
1
a
故选 B.
6.【答案】A
1
【解析】由题意得直线 kx y 4 0
经过圆心C ,3
k
,所以 3 4 0 ,解得 k 2,
2 2
故选 A
7.【答案】 x2 y2 2x 6y 19 0
【解析】因为点 A(-4,-5),B(6,-1)
所以圆心为: 1, 3 ABr 100 16, 29
2 2
所以圆的标准方程为: x 1 2 y 3 2 29
2 2
所以圆的一般方程为: x y 2x 6y 19 0
x2故填 y2 2x 6y 19 0
8.【答案】6
2 2
【解析】由题设可得圆的标准方程为: x 1 y 3 9,
所以圆的半径为R 3,故周长为2 R 6 .
故填6 .
9.【答案】 ( 1
1
, ) (
3 ,2)
2 2
【解析】因为方程 x2 y2 2y m2 m 1 0表示圆,
所以 ( 2)2 4(m2 m 1) 0 ,
得m2 m 2 0,解得 1 m 2.
因为点 (1,
3)在圆 x2 y2 2y m2 m 1 0外,
2
12 (3)2 2 3 m2所以 m 1 0 ,
2 2
1 3
即 4m2 4m 3 0 ,解得m 或m .
2 2
综上,实数m 的取值范围是 ( 1 1, ) (3 ,2) .
2 2
故填 ( 1
1) (3, , 2) .
2 2
10.【答案】(1) 1,4 5;(2) .
2
1 2 2【解析】( ) x m y 2 m2 3m 4 0 1 m 4 ,即实数m 的取值范围是 1,4 ;
3 2 25 25 3 5
(2)R2 m2 3m 4 m
≤ ,当且仅当m 时,半径R 取得最大值 .
2 4 4 2 2
2.5.1 直线与圆的位置关系
基础练
一、单选题
1.直线 y x 2与圆 x2 y2 4 有( )个公共点.
A.0 B.1 C.2 D.3
2.圆 x2 y2 4x 2y 2 0截 x 轴所得弦的长度等于( )
A.2 2 B.2 3 C.4 2 D.2
3.若直线 y 3x b x2与圆 y2 1相切,则b ( )
A 2 3. B. 2 C. 2 D. 5
3
4.已知直线 l :3x 4y m 0被圆C : x2 y2 2x 2y 6 0 截得的弦长为 2 7 ,则m 的值为( )
A.4 或-6 B.-4 或 6 C.4 或 6 D.-4 或-6
5 2 2.已知圆 (x 2) ( y 1) 12 上恰有三个点到直线 l : kx y 0 距离等于 3 ,则直线 l 的斜率为( )
A.2 6 B. 2 6 C. 6 2 D. 6 2
6 2.圆C : x y2 2x 4y 3 0 被直线 l : a x y 1 a 0截得的弦长的最小值为( )
A.1 B.2 C. 2 D. 3
二、填空题
7 2 2.过点M (1, 3) 作圆O : x y 4的切线方程是__________.
8.直线 y=2﹣x x2 y2与圆 4x 5 0 交于 A,B 两点,则|AB|=_____.
9 2 2.过点P(1,1) 作圆 x y 2x 1 0的切线,切点为 A ,则 PA ________.
三、解答题
10.已知圆心为 C(4,3)的圆经过原点 O.
(1)求圆 C 的方程;
(2)设直线 3x﹣4y+15=0 与圆 C 交于 A,B 两点,求△ABC的面积.
参考答案
1.【答案】C
【解析】圆 x2 y2 4 的圆心为坐标原点O 0,0 ,半径 r 2 ,
直线 y x 2的方程化为一般式为: x y 2 0 ,
0 0 2
圆心O到直线 y x 2的距离d 2 r ,
12 12
∴直线 y x 2 2 2与圆 x y 4相交,∴有 2 个公共点,
故选 C.
2.【答案】A
x2 y2【解析】在圆方程 4x 2y 2 0中令 y 0,
得 x2 4x 2 0 x 4 8 2 2
2
因此弦长为| 2 2 ( 2 2) | 2 2
故选 A
3.【答案】C
【解析】由题得圆的圆心坐标为(0,0),
|b |
所以 1, b 2 .
3 1
故选 C
4.【答案】A
2
【解析】圆C 的标准方程为: x 1 y 1 2 8,
故圆心C 到直线 l的距离为d 8 27 1,
3 4 m
所以 1,故m 6或m 4 ,
9 16
故选 A.
5.【答案】A
| 2k 1|
【解析】由题意,圆心到直线 l的距离等于半径的一半,所以 32 ,解得k 2 6 ,k 1
故选 A.
6.【答案】B
【解析】直线 l : a x y 1 a 0可化为 l : a(x 1) (y 1) 0 ,故直线 l恒过点P 1,1 .
圆C : x2 y2 2x 4y 3 0的圆心为C(1,2) ,半径为 2 当直线 l 垂直于直线PC 时,截得的弦
长最短,此时弦长d 2 2 1 2 .
故选 B
7.【答案】 x 3y 4 0
【解析】因为点M 1, 3 2 2 1 3在圆O : x y 4上,所以切点为M 1, 3 ,切线斜率k kOM 3
3
所以由点斜式写方程得 y x 1 3 即 x 3y 4 0
3
故填 x 3y 4 0
8.【答案】2.
2 2 2
【解析】根据题意,圆 x y 4x 5 0 ,即 x 2 y2 9,其圆心为 2,0 ,半径 r 3,
2 2
圆心到直线 y 2 x的距离d 2 2 ,
1 1
则弦长 AB 2 r2 d 2 2 9 8 2 .
故填2 .
9.【答案】 3
2 2
【解析】由题得 (x 1) y 2,所以圆C 的圆心为 ( 1,0) ,半径为 2 .
所以 | PC | (1 1)2 12 5 ,
2 2
所以 | PA | 5 2 3 .
故填 3
10.【答案】(1)(x﹣4)2+(y﹣3)2=25.(2)12
【解析】(1)圆 C 的半径为 OC 32 42 5,
从而圆 C 的方程为(x﹣4)2+(y﹣3)2=25;
(2)作 CD⊥AB 于 D,则 CD 平分线段 AB,
在直角三角形 ADC中,由点到直线的距离公式,得|CD|=3,
所以 AD AC |2 CD |2 4,
所以|AB|=2|AD|=8,
1
所以△ABC 的面积S AB CD 12.
2
2.5.2 圆与圆的位置关系
基础练
一、单选题
1.圆 (x 3)2 (y 2)2 4与圆 (x 7)2 (y 1)2 36的位置关系是( )
A.相切 B.内含 C.相离 D.相交
2.圆 x2 y2 1和圆 x2 y2 6y 5 0的位置关系是( )
A.内含 B.内切 C.外切 D.外离
3.圆 C1:x2+y2=16与圆 C2:(x-3)2+(y-4)2=9 的公共弦的长为( )
12 16 24 32
A. B. C. D.
5 5 5 5
4 2.圆C1 : x y
2 2x 2y 2 0与C2 : x
2 y2 4x 2y 1 0的公切线有且仅有( )
A.1条 B.2条 C.3条 D.4条
5 C x2 y2 4x 6y 12 0 C x 4 2 y 5 2.若圆 1 : 与圆 2 : m 有且仅有 3 条公切线,则实数 m
的值为( )
A.4 B.25 C.5 D.16
6.若圆C1 : x
2 y2 4 2 2与圆C2 : x y 6x 8y m 0外切,则实数m ( )
A. 24 B. 16 C.24 D.16
二、填空题
7 x2 y2 x 0 x2 y2.圆 与圆 2y 0的公共弦所在的直线方程为___________.
8 O 2 2 2 2.若⊙ 1 : x y 5与⊙O2 : (x m) y 20(m R) 相交于 A、B 两点,且两圆在点 A 处的切线互
相垂直,则线段 AB 的长度是 .
9 2 2 2 2.圆C1 : x m y 2 9与圆C2 : x 1 y m 4内切,则m 的值为______.
三、解答题
10.已知两圆C1 : (x 1)
2 (y 1)2 4 C : x2 y2和 2 4ax 2y 4a
2 0 .
(1)把圆C2 化成标准方程;
(2)试求当 a为何值时,两圆C1 和C2 相切.
参考答案
1.【答案】D
【解析】两圆的圆心分别为: A(3, 2),B(7,1),
半径分别为: r 2, R 6,
两圆心距为: | AB | (7 3)2 (1 2)2 5
R r | AB| R r,
所以,两圆相交,
故选 D。
2.【答案】C
2 2 2 2
【解析】∵圆 x y 6y 5 0的标准方程为: x (y 3) 4,
表示以 (0,3)为圆心,半径为 2的圆,
∴两圆圆心距为3,正好等于半径之和,
∴两圆相外切,
故选C .
3.【答案】C
【解析】两圆方程相减得公共弦方程为3x 4y 16 0 ,圆心C1 0,0 ,到公共弦的距离为
16
d 16
2
, 16 24所以所求弦长为 2 42 .32 42 5 5 5
故选 C
4.【答案】B
【解析】圆C1 的标准方程为 x 1 2 y 1 2 4 2,圆C2 的标准方程为 x 2 y 1 2 4,
两圆心分别为C1 1, 1 、C2 2,1 ,半径分别为 r1 r2 2,
C1C2 11 r1 r2 4,两圆相交,因此,两圆有2条公切线,
故选 B.
5.【答案】B
2
【解析】依题意,圆C1 : x 2 y 3 2 25,
由题得C1 与C2 外切,
则 C1C2 r1 r2 ,
故 2 4 2 3 5 2 5 m ,
解得m 25,
故选 B.
6.【答案】D
【解析】圆C1 的圆心为 0,0 ,半径为2,圆C2 的圆心为 3,4 ,半径为 25 m .
两个圆的圆心距为 32 42 5 .
由于两个圆外切,所以 2 25 m 5,解得m 16 .
故选 D
7.【答案】 x 2y 0
【解析】由题:圆 x2 y2 x 0 2 2与圆 x y 2y 0的标准方程为:
1 2 2
x
y
2 1 和 x2 y 1 1,
2 4
5 1 5 3
圆心距为 , ,
2 2 2 2
所以两圆相交,
2 2 2 2
所以公共弦所在直线方程即: x y x x y 2y 0,
即 x 2y 0 .
故填 x 2y 0
8.【答案】4
1 AB 1
【解析】依题意得OO1= 5 20 =5,且△OO1A是直角三角形,S△OO1A= · ·OO1= ·OA·AO1,
2 2 2
2 OA AO 2 5 2 5
因此 AB= 1= =4.
OO1 5
故填 4
9.【答案】 2或 1
【解析】圆C1 的圆心为 m, 2 ,半径为 r1 3,
圆C2 的圆心为 1,m ,半径为 r2 2,
2
所以两圆的圆心距d m 1 m 2 2 ,
m 1 2 m 2 2又因为两圆内切,有 1,
解得m 2或m 1.
故填 2或 1.
10 2 2.【答案】(1)C2 : (x 2a) (y 1) 1;(2)a 0或 1时内切;a 1或 2 时外切.
2 2
【解析】(1)圆C2 的标准方程为:C2 : (x 2a) (y 1) 1;
(2 2)圆C1 : (x 1) (y 1)
2 4的圆心C1 : ( 1,1),半径R1 2,
圆C2 : (x 2a)
2 (y 1)2 1的圆心C2 : (2a,1),半径R2 1,
当两圆外切时: 1 2a 1+2 3,解得 a 1或 2 ;
当两圆内切时: 1 2a 2 1 1,a 0或 1.
2.5.3 直线与圆的综合
基础练
一、单选题
1.已知圆C : x2 2x y2 0 ,则圆心C 到直线 x 3的距离等于( )
A.1 B.2 C.3 D.4
2.已知直线 l : x 3y 0与圆C : x2 (y 1)2 1相交于O, A两点,O为坐标原点,则 COA的面积为
( )
A 3 B 3. . C. 3 D.2 3
4 2
3.已知点 P(2,1)在圆 C:x2+y2+ax–2y+b=0 上,点 P 关于直线 x+y–1=0 的对称点也在圆 C 上,则圆 C
的圆心坐标为( )
A.(0,1) B.(1,0) C.(2,1) D.(1,2)
4 y x 1 x2 y2.垂直于直线 且与圆 4 相切于第三象限的直线方程是( )
A. x y 2 2 0 B. x y 2 0
C. x y 2 0 D. x y 2 2 0
5 2 2.直线 x y 2 0截圆 x y 4 所得劣弧所对圆心角为( )
2
A. B. C. D.
6 3 2 3
6.已知圆C 的圆心在曲线 y 3 x 0 上,直线 l过 3,3 且与直线4x 3y 5 0垂直,则与直线 l 相
x
切的面积最小的圆C 的方程为( )
2 2
A. x 2 2 y 3 3
3 B. x 2
2 y
9
2 2
2 2
C 3 3 3 . x y 2 3 D. x y 2
2 9
2 2
二、填空题
7 2 2.过圆 x y 36内的一点 A 2,4 引此圆的弦MN ,则 MN 的最小值为______.
8.已知直线 l与圆 x2 y2 2y 0相交于 A, B
1 1
两点,且线段 AB 的中点 P 坐标为 , ,则直线 l 的方
2 2
程为__________.
9.经过原点并且与直线 x y 2 0相切于点 2,0 的圆的标准方程是__________.
三、解答题
10.已知圆C : (x 3)2 (y 4)2 4和直线 l : kx y 4k 3 0
(1)求证:不论 k 取什么值,直线 l和圆 C 总相交;
(2)求直线 l被圆 C 截得的最短弦长及此时的直线方程.
参考答案
1.【答案】D
【解析】由题 x 2 1 y2 1 ,则圆心(-1,0),则圆心C 到直线x 3的距离等 3-(-1)=4
故选 D
2.【答案】A
【解析】由题意直线 l,圆C 均过原点,通过图形观察可知 COA为等腰三角形,且CO CA r 1,
OCA 120 1 1 3 3,所以 S 2 . COA CO CA sin OCA 1 2 2 2 4
故选 A.
3.【答案】A
【解析】依题意有:如图所示,根据图形的对称性可知:点P 2,1 关于直线 x y 1 0对称的点是
点Q 3 2a b 00, 1 ,分别将P,Q 两点的坐标代入圆的方程得 ,解得a 0,b 3,而圆心坐
b 3 0
a ,1 标为 ,故圆心坐标为 0,1 .
2
故选 A
4.【答案】A
【解析】设所求的直线为 l,
直线 l垂直于直线 y x 1,可得直线 l的斜率为k 1,
设直线 l方程为 y x b,即 x y b 0,
2 2
又直线 l与圆 x y 4 相切,
圆心O(0,0) 到直线 l的距离 d
| b |
2,
2
解得b 2 2
当b 2 2 时,可得切点坐标 2, 2 ,切点在第三象限;
当b 2 2 时,可得切点坐标 2, 2 ,切点在第一象限;
直线 l x2 y2与圆 1的切点在第三象限,
取b 2 2 ,此时的直线方程为 x y 2 2 0.
故选 A.
5.【答案】D
【解析】由题意有,该圆圆心为 (0,0) ,半径为 2,
2
圆心到直线的距离d 1,
2
∴弦长 l 2 22 12 =2 3 ,
22 22 cos (2 3)
2 1
由余弦定理得圆心角 的余弦值 ,
2 2 2 2
2
∴圆心角 = .
3
故选 D.
6.【答案】B
3
【解析】依题意,设圆C 的圆心坐标为 a, a
a 0 .设直线 l:3x 4y b 0,将 3,3 代入可
知,b 3,故直线 l的方程为3x 4y 3 0;
因为直线 l与故圆C 相切,
12 12
故圆C 3a 3 2 3a 3 12的半径 a a ,当且仅当3a ,即a 2时,等号成立,此R 3 a
5 5
3 22
时圆C 的方程为 x 2 y 9 .
2
故选 B.
7.【答案】8
【解析】如图,
由平面几何知识得,当过点 A的弦MN 垂直于OA时,MN 最短,
所以 MN 2 36
min 22 42 8.
故填 8.
8.【答案】 x y 0
2
【解析】把圆的方程化为标准方程得: x2 y 1 1,
可得圆心C(0,1), 直线CP的斜率为 1,
直线 AB 的斜率为 1,
1 1
则直线 AB 的方程为: y (x ),即 x y 0.
2 2
故填 x y 0.
9 x 1 2 y 1 2.【答案】 2
【解析】设圆心坐标 (a,b),则a2
b
b2 r2, (a 2)2 b2 r 2 , 1,根据这三个方程组可以a 2
2 2
计算得:a 1,b 1, r 2 ,所以所求方程为: (x 1) (y 1) 2 ,
2 2
故填 x 1 y 1 2
10.【答案】(1)详见解析;(2)2 2 , x y 1 0 .
【解析】(1)由直线 l的方程 y 3 k x 4 可得直线 l 恒通过点 4,3 ,而点 4,3 在圆C 的内部,
故得到不论k 取什么值,直线 l和圆 C 总相交;
(2)设定点为 A 4,3 k 4 3,因为 CA 1,求出直线 l的斜率,即可写出直线 l 的方程,3 4
求出圆心到直线 l的距离d ,即可求出弦长。
解析:(1)证明:由直线 l的方程可得, y 3 k x 4 ,则直线 l恒通过点
4,3 ,把 4,3 2 2代入圆的C 方程,得 4 3 3 4 2 4 ,
所以点 4,3 在圆C 的内部,又因为直线 l恒过点 4,3 ,
所以直线 l与圆C 总相交.
(2)设定点为 A 4,3 ,由题可知当直线 l与CA直线垂直时,直线 l被圆C 截得的弦长最短,
4 3
因为 kCA 1,所以直线 l的斜率为k 13 4
所以直线 l的方程为 y 3 x 4,即 x y 1 0
3 4 1设圆心C 3,4 到直线 l距离为d ,则d 2
2
2
所以直线 l被圆C 截得最短的弦长为2 4 2 2 2 .
2.6 章末复习课
基础练
一、单选题
l 0 2
1.若直线 的倾斜角 满足 ,且 ,则其斜率
3 k 满足( )2
A. 3 k 0 B. k 3
C k 0 k 3 D k 0 k 3. 或 . 或
3
2.点 1,1 在圆 x2 y 1 2 1的( )
A.圆上 B.圆内 C.圆外 D.无法判定
3.设直线 l的方程为2x 4y 3 0,直线m 的方程为 x 2y 6 0,则直线 l与m 的距离为( )
A 3 5 B 3 5 C 9 5 D 9 5. . . .
10 5 10 5
4 x 2 2.圆 y2 4 x 2 2 y 3 2与圆 25的位置关系为( )
A.内切 B.外切 C.相交 D.相离
5 2 2.已知定点B 3,0 ,点 A在圆 (x 1) y 4上运动,则线段 AB 的中点M 的轨迹方程是( )
A (x 1)2. y2 1 B. (x 2)2 y2 4
C 2 2. (x 1) y 1 D. (x 2)2 y2 4
6.以 1,m 为圆心,且与两条直线 2x y 4 0,2x y 6 0都相切的圆的标准方程为( )
A. x 1 2 y 9 2 5 B x 1 2. y 11 2 25
C. x 2 2 1 y 1 5 D 2. x 1 y 9 2 25
二、填空题
7.直线3x 2y k 0在两坐标轴上的截距之和为2,则实数 k ______.
8.若圆 (x 1)2 (y 4)2 5的圆心到直线 x y a 0 2的距离为 ,则a 的值为_________.
2
9.已知圆C : (x 1)2 (y 2)2 5,过圆C 外一点P 3,4 作圆的两条切线PA,PB切点分别为 A,B ,
则直线 AB 的方程为_______.
三、解答题
10 C : x2 y2 2x 8 C : x2 4ax y2 2y 3 4a2.已知圆 1 ,圆 2
(1)若 a 1,求两圆心连线C1C2 的中垂线的一般式方程;
(2)若 a 1,且动点 P 满足PC1 2PC2 ,求 P 点轨迹方程;
(3)若两圆相切,求 a的值.
参考答案
1.【答案】C
k tan 0 2
【解析】斜率 ,因为 ,且 ,3 2
故 tan 0或 tan 3 ,即 k 0或 k 3 ,
故选 C.
2.【答案】A
【解析】将点 1,1 的坐标代入圆 x2 y 1 2 1的方程即12 1 1 2 1,∴点 1,1 在圆 x2 y 1 2 1
上,
故选 A.
3.【答案】C
3 12
【解析】直线m 的方程可化为2x 4y 12 0,因此,直线 l与m 9 5的距离为d .
22 42 10
故选 C.
4.【答案】C
2
【解析】根据题意,圆(x 2) y2 4的圆心为 ( 2,0) ,半径 r1 2 ;
圆 x 2 2 y 3 2 25的圆心为 (2,3) ,半径 r2 5 ;
两圆的圆心距d 42 32 5,有5 2 d 5 2,
则两圆相交;
故选 C.
5.【答案】C
xA 3 yA xA 2x 3
【解析】设M x, y ,则 A xA, yA 满足 , x, y .故 .故 A 2x 3,2y . 2 2 yA 2y
2 2
又点 A在圆 (x 1) y 4上.故 (2x 3 1)2 2y 2 4 x 1 2 y2 1 .
故选 C
6.【答案】C
2 m 4 2 m 6
【解析】设圆的半径为 r ,则 r ,
5 5
m 1
则 ,
r 5
2
即圆的标准方程为 x 1 y 1 2 5,
故选 C.
7.【答案】12
x 0 y k【解析】令 ,则 ;令 y 0,则 x k ,
2 3
k k
故
2,解得k 12 .2 3
故填12 .
8.【答案】4或 2
3 a
【解析】圆 (x 1)2 2 (y 4)2 5的圆心为 1, 4 ,它到直线 x y a 0的距离为 ,
2 2
故a 2或a 4 .
故填 4 或 2.
9.【答案】2x 6y 5 0.
【解析】设 A x1, y1 ,B x2 , y2 ,则切线PA的方程为
x1 1 x 1 y1 2 y 2 5,因为点P 3,4 在切线PA上,所以切线PA的方程为
2x1 6y1 5,即2x1 6y1 5 0①,同理,切线PB的方程为2x2 6y2 5 0②,由①②得,
直线 AB 的方程为2x 6y 5 0.
故填2x 6y 5 0.
10.【答案】(1)3x y 2 0;(2) x 5 2 1 y 2 2 20 3 a 2 6 1;( ) 或a
2 2
【解析】(1)当 a 1时,
圆C1 : x
2 y2 2x 8 x 1 2,即为 y2 9,圆心为C1 1,0 ,
C : x2 4x y2 2y 3 4 C : x 2 2 y 1 2圆 2 ,即 2 4,圆心为C2 2, 1 ,
1 1 0 1 1
则两圆心的中点坐标为 , , kC C , 2 2 1 2 1 2 3
1 1
两圆心连线C1C2 的中垂线为: y 3 x ,
2 2
整理得一般式为:3x y 2 0;
(2)设P x, y ,C1 1,0 ,C2 2, 1 ,
PC1 2PC
2
2,即PC1 2PC
2
2 ,
x 1 2 y2 2 x 2 2 y 1 2 ,
2 2
整理得 P 点轨迹方程为 x 5 y 2 20 ;
(3)圆C1 : x
2 y2 2x 8,即为 x 1 2 y2 9,圆心为C1 1,0 ,
C : x2圆 2 4ax y
2 2y 3 4a2 ,即C2 : x 2a
2 y 1 2 4,圆心为C2 2a, 1 ,
若两圆相切,
2 2 6 1
当两圆外切时: 2a 1 12 3 2,解得a ;
2
当两圆内切时: 2a 1 2 12 3 2,解得a
1
,
2
a 2 6 1
1
综合得:若两圆相切, 或 a .
2 2
