广东省汕头市澄海区高级中学2021-2022学年高二上学期第一次月考数学试题(Word版含答案)
文档属性
| 名称 | 广东省汕头市澄海区高级中学2021-2022学年高二上学期第一次月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 18:53:38 | ||
图片预览



文档简介
澄海中学2021-2022学年度第一学期第一次月考
高二级数学科试题
本试卷分选择题和非选择题两部分,共4页,满分150分.考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、座位号、准考证号用2B铅笔涂写在答题卡上.
2.答选择题时,必须用2B铅笔把答题卡上对应题号的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.
3.答非选择题时,必须用黑色签字笔或钢笔,将答案写在答题卡上规定的位置上.
4.考试结束后,监考人将答题卡收回,试卷考生自己保管.
第一部分(选择题,共60分)
一、单项选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.
1.已知集合,则集合A∩B=( )
A. B. C. D.
2.复数z满足,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如下图,直线的方程是( )
A. B.
C. D.
4.设为定义在上的偶函数,且在上为增函数,则的大小顺序是( )
A. B.
C. D.
5.为了得到函数的图像,只需将函数的图像( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
6.已知函数,则不等式的解集为( )
A. B. C. D.
7.在四面体中,底面,,,则四面体的外接球的表面积是( )
A. B. C. D.
8.己知是第四象限角,化简为( )
A. B. C. D.
二、多项选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得 5 分,部分选对的得 3 分,有选错的得 0 分)
9.如果,,那么直线经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.已知空间中三点,则下列结论正确的有( )
A.与是共线向量
B.与共线的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
11.已知,表示平面,,表示直线,以下命题中不正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
12.有6个相同的球,分别标有数字1,2,3,4,5,6.从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”.丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙不相互独立 D.丙与丁相互独立
第二部分(非选择题,共90分)
三、填空题:本题共4个小题,每小题5分,共20分。把答案填在答题卷相应横线上.
13. 若经过,两点的直线的倾斜角为,则________.
14.如图所示,点、、分别在空间直角坐标系的三条坐标轴上,,平面的一个法向量为,平面与平面的夹角为,则________.
15.若实数满足,则的最大值是___________.
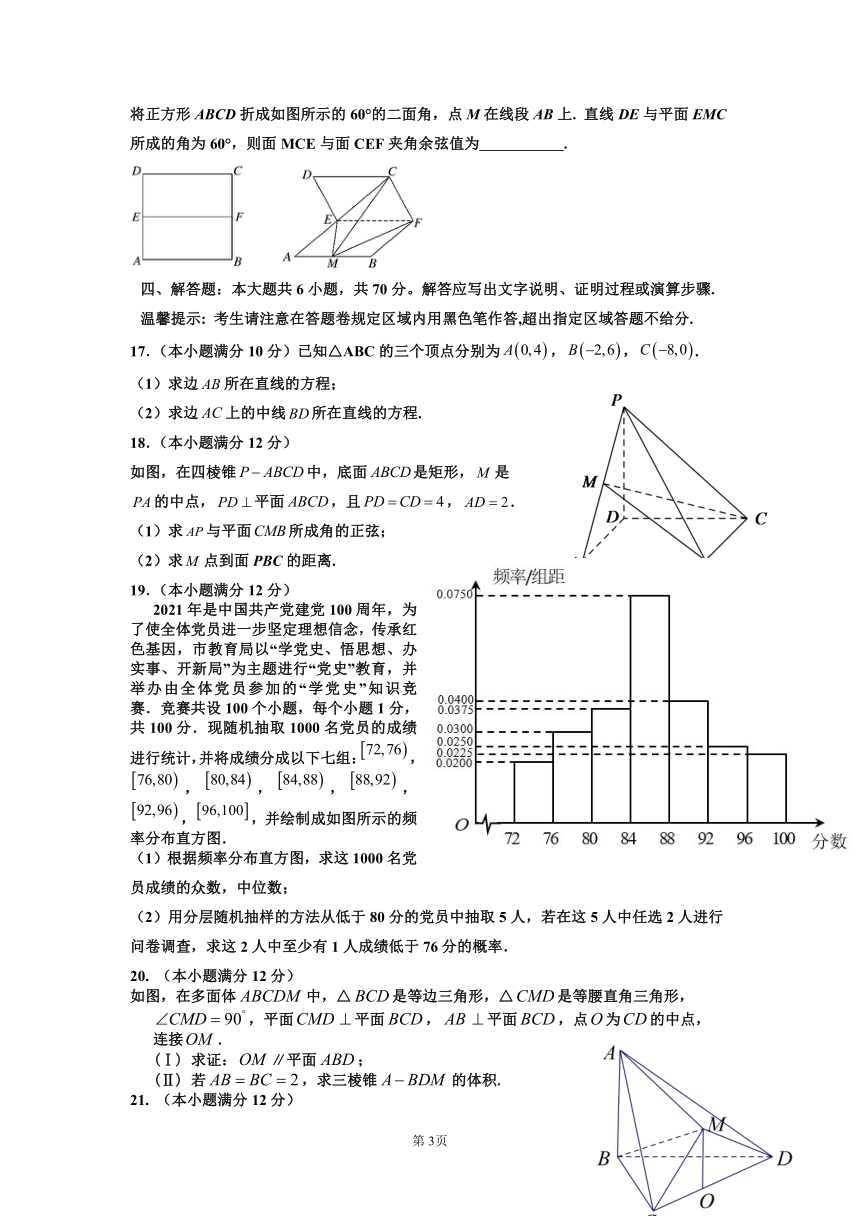
16. 已知正方形的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上. 直线DE与平面EMC所成的角为60°,则面MCE与面CEF夹角余弦值为___________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
温馨提示: 考生请注意在答题卷规定区域内用黑色笔作答,超出指定区域答题不给分.
17.(本小题满分10分)已知△ABC的三个顶点分别为,,.
(1)求边所在直线的方程;
(2)求边上的中线所在直线的方程.
18.(本小题满分12分)
如图,在四棱锥中,底面是矩形,是
的中点,平面,且,.
(1)求与平面所成角的正弦;
(2)求点到面PBC的距离.
19.(本小题满分12分)
2021年是中国共产党建党100周年,为了使全体党员进一步坚定理想信念,传承红色基因,市教育局以“学党史、悟思想、办实事、开新局”为主题进行“党史”教育,并举办由全体党员参加的“学党史”知识竞赛.竞赛共设100个小题,每个小题1分,共100分.现随机抽取1000名党员的成绩进行统计,并将成绩分成以下七组:,,,,,,,并绘制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求这1000名党员成绩的众数,中位数;
(2)用分层随机抽样的方法从低于80分的党员中抽取5人,若在这5人中任选2人进行问卷调查,求这2人中至少有1人成绩低于76分的概率.
20. (本小题满分12分)
如图,在多面体中,△是等边三角形,△是等腰直角三角形,
,平面平面,平面,点为的中点,
连接.
(Ⅰ) 求证:∥平面;
(Ⅱ) 若,求三棱锥的体积.
21. (本小题满分12分)
已知函数.
(1)求的最小正周期和单调递增区间;
(2)求函数在区间上的值域
(3)在锐角中,角A、B、C的对边分别为,,,若,,求面积的最大值.
22.(本小题满分12分)
已知函数是定义在[,1]上的奇函数,且.
(1)求a,b的值;
(2)判断在[,1]上的单调性,并用定义证明;
(3)设,若对任意的,总存在,使得成立,求实数k的取值范围.
2021-2022第一学期高二数学第一次月考考试参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
B A D A D B D B ACD CD ABD BC
二、填空题
【答案】2 14. 【答案】 15. 【答案】 16. 【答案】
7. 【答案】D如图,在四面体中,底面,,,可得,所以,补形为长方体,则过一个顶点的三条棱长分别为1,1,,则长方体的对角线长为,则三棱锥的外接球的半径为1.其表面积为.故选:D.
8.【答案】B【详解】∵为第四象限角,
∴.故选:B
12.解:由题意可得,P(甲)=,P(乙)=,,P(丁)=,
P(甲丙)=0≠P(甲)P(丙),P(甲丁)=P(甲)P(丁)=,
P(乙丙)=,P(丙丁)=0≠P(丁)P(丙).故选:BC.
16. 详解:由已知可得,EF⊥AE,EF⊥DE,所以EF⊥平面ADE,所以平面ABFE⊥平面ADE.取AE的中点H为坐标原点,建立如图所示的空间直角坐标系,
所以,
所以
设 (0≤t≤4),则,设平面EMC的法向量,则所以,取y=-2,则,所以.因为DE与平面EMC所成的角为60°,所以
所以,解得t=1或t=3,t=1或t=3时,直线DE与平面EMC所成的角为60°.
取ED的中点Q,则为平面CEF的法向量.因为点Q的坐标为
所以 , ,设MCE与面CEF夹角为.
所以.
所以当t=1时, ,.当t=3时, .
17.(1)由两点式得边所在直线的方程为,即;5分
(2)由题意,得点的坐标为(-4,2), 7分
由两点式,得所在直线的方程为,即.10分
18.【详解】(1)因为底面是矩形,平面,
所以以为原点,分别为轴,建立空间直角坐标系,如图所示:
EMBED Equation.DSMT4 ,,,,,
,,,…………2分
设平面的法向量,
则,令,即,…………4分
设与平面所成角为,则…………6分
(2),,…………7分
设平面的法向量则,令,即,9分
设点到面PBC的距离为,则…………12分
19.【详解】(1)由频率分布直方图可得,1000名党员成绩的众数为,……2分
成绩在的频率为,
成绩在的频率为,
故中位数位于之间,中位数是………………………………5分.
(2)∵与的党员人数的比值为2:3,
采用分层随机抽样方法抽取5人,则在中抽取2人,中抽3人,
设抽取人的编号为,,抽取人的编号为,,,…………7分
则从5人中任选2人进行问卷调查对应的样本空间为:
,,,,,,,,,,共10个样本点, ………………9分
这2人中至少有1人成绩低于76分的有:
,,,,,,,共7个样本点,11分
故这2人中至少有1人成绩低于76分的概率.………………………………12分
20. (Ⅰ)证明:∵ △是等腰直角三角形,,点为的中点,
∴ . ………………………………………1分
∵ 平面平面,平面∩平面,平面,
∴ 平面.………………………………2分
∵ 平面,
∴ ∥.………………………………………3分
∵ 平面,平面,
∴ ∥平面.………………………………4分
(Ⅱ)解法1:由(Ⅰ)知∥平面,
∴ 点到平面的距离等于点到平面的距离.
过作,垂足为点,
∵ 平面,平面,
∴ . ………………………………………6分
∵ 平面,平面,,
∴ 平面. ………………………………………7分
∵ ,△是等边三角形,
∴ ,,.………………………………9分
∴ ………………………………………10分
.
∴ 三棱锥的体积为. …………12分
解法2: 由(Ⅰ)知∥平面,
∴ 点到平面的距离等于点到平面的距离. …………………5分
∵ ,△是等边三角形,
∴ ,. ………………………………………6分
连接, 则, . ……………………………7分
∴ ………………………………………10分
.
∴ 三棱锥的体积为. ………………………………………12分
21. 解:(1)
3分
∴的最小正周期. …………………………4分
由得
∴的单调递增区间为 ……6分
(2)
∴函数在区间上的值域为
(3)由,由为锐角,得.……………………8分
由余弦定理,得.……10分
∴,当且仅当时等号成立.…………………………………………11分
∴.∴面积的最大值为. ……12分
22.【详解】(1)依题意函数是定义在[,1]上的奇函数,所以,,所以,经检验,该函数为奇函数.…………………3分
(2)在上递增,证明如下:任取,
,…………6分
其中,所以,
故在上递增.……………………………………………………7分
(3)由于对任意的,总存在,使得成立,所以.……………8分
.……………………………………9分
当时,在上递增,,所以.………10分
当时,在上递减,,所以.……………11分
综上所述,.…………………12分
第5页
高二级数学科试题
本试卷分选择题和非选择题两部分,共4页,满分150分.考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、座位号、准考证号用2B铅笔涂写在答题卡上.
2.答选择题时,必须用2B铅笔把答题卡上对应题号的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案.
3.答非选择题时,必须用黑色签字笔或钢笔,将答案写在答题卡上规定的位置上.
4.考试结束后,监考人将答题卡收回,试卷考生自己保管.
第一部分(选择题,共60分)
一、单项选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.
1.已知集合,则集合A∩B=( )
A. B. C. D.
2.复数z满足,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如下图,直线的方程是( )
A. B.
C. D.
4.设为定义在上的偶函数,且在上为增函数,则的大小顺序是( )
A. B.
C. D.
5.为了得到函数的图像,只需将函数的图像( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
6.已知函数,则不等式的解集为( )
A. B. C. D.
7.在四面体中,底面,,,则四面体的外接球的表面积是( )
A. B. C. D.
8.己知是第四象限角,化简为( )
A. B. C. D.
二、多项选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得 5 分,部分选对的得 3 分,有选错的得 0 分)
9.如果,,那么直线经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.已知空间中三点,则下列结论正确的有( )
A.与是共线向量
B.与共线的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
11.已知,表示平面,,表示直线,以下命题中不正确的选项是( )
A.假设,,那么
B.假设,,,那么
C.假设,,那么
D.假设,,,,那么
12.有6个相同的球,分别标有数字1,2,3,4,5,6.从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”.丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙不相互独立 D.丙与丁相互独立
第二部分(非选择题,共90分)
三、填空题:本题共4个小题,每小题5分,共20分。把答案填在答题卷相应横线上.
13. 若经过,两点的直线的倾斜角为,则________.
14.如图所示,点、、分别在空间直角坐标系的三条坐标轴上,,平面的一个法向量为,平面与平面的夹角为,则________.
15.若实数满足,则的最大值是___________.
16. 已知正方形的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上. 直线DE与平面EMC所成的角为60°,则面MCE与面CEF夹角余弦值为___________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
温馨提示: 考生请注意在答题卷规定区域内用黑色笔作答,超出指定区域答题不给分.
17.(本小题满分10分)已知△ABC的三个顶点分别为,,.
(1)求边所在直线的方程;
(2)求边上的中线所在直线的方程.
18.(本小题满分12分)
如图,在四棱锥中,底面是矩形,是
的中点,平面,且,.
(1)求与平面所成角的正弦;
(2)求点到面PBC的距离.
19.(本小题满分12分)
2021年是中国共产党建党100周年,为了使全体党员进一步坚定理想信念,传承红色基因,市教育局以“学党史、悟思想、办实事、开新局”为主题进行“党史”教育,并举办由全体党员参加的“学党史”知识竞赛.竞赛共设100个小题,每个小题1分,共100分.现随机抽取1000名党员的成绩进行统计,并将成绩分成以下七组:,,,,,,,并绘制成如图所示的频率分布直方图.
(1)根据频率分布直方图,求这1000名党员成绩的众数,中位数;
(2)用分层随机抽样的方法从低于80分的党员中抽取5人,若在这5人中任选2人进行问卷调查,求这2人中至少有1人成绩低于76分的概率.
20. (本小题满分12分)
如图,在多面体中,△是等边三角形,△是等腰直角三角形,
,平面平面,平面,点为的中点,
连接.
(Ⅰ) 求证:∥平面;
(Ⅱ) 若,求三棱锥的体积.
21. (本小题满分12分)
已知函数.
(1)求的最小正周期和单调递增区间;
(2)求函数在区间上的值域
(3)在锐角中,角A、B、C的对边分别为,,,若,,求面积的最大值.
22.(本小题满分12分)
已知函数是定义在[,1]上的奇函数,且.
(1)求a,b的值;
(2)判断在[,1]上的单调性,并用定义证明;
(3)设,若对任意的,总存在,使得成立,求实数k的取值范围.
2021-2022第一学期高二数学第一次月考考试参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
B A D A D B D B ACD CD ABD BC
二、填空题
【答案】2 14. 【答案】 15. 【答案】 16. 【答案】
7. 【答案】D如图,在四面体中,底面,,,可得,所以,补形为长方体,则过一个顶点的三条棱长分别为1,1,,则长方体的对角线长为,则三棱锥的外接球的半径为1.其表面积为.故选:D.
8.【答案】B【详解】∵为第四象限角,
∴.故选:B
12.解:由题意可得,P(甲)=,P(乙)=,,P(丁)=,
P(甲丙)=0≠P(甲)P(丙),P(甲丁)=P(甲)P(丁)=,
P(乙丙)=,P(丙丁)=0≠P(丁)P(丙).故选:BC.
16. 详解:由已知可得,EF⊥AE,EF⊥DE,所以EF⊥平面ADE,所以平面ABFE⊥平面ADE.取AE的中点H为坐标原点,建立如图所示的空间直角坐标系,
所以,
所以
设 (0≤t≤4),则,设平面EMC的法向量,则所以,取y=-2,则,所以.因为DE与平面EMC所成的角为60°,所以
所以,解得t=1或t=3,t=1或t=3时,直线DE与平面EMC所成的角为60°.
取ED的中点Q,则为平面CEF的法向量.因为点Q的坐标为
所以 , ,设MCE与面CEF夹角为.
所以.
所以当t=1时, ,.当t=3时, .
17.(1)由两点式得边所在直线的方程为,即;5分
(2)由题意,得点的坐标为(-4,2), 7分
由两点式,得所在直线的方程为,即.10分
18.【详解】(1)因为底面是矩形,平面,
所以以为原点,分别为轴,建立空间直角坐标系,如图所示:
EMBED Equation.DSMT4 ,,,,,
,,,…………2分
设平面的法向量,
则,令,即,…………4分
设与平面所成角为,则…………6分
(2),,…………7分
设平面的法向量则,令,即,9分
设点到面PBC的距离为,则…………12分
19.【详解】(1)由频率分布直方图可得,1000名党员成绩的众数为,……2分
成绩在的频率为,
成绩在的频率为,
故中位数位于之间,中位数是………………………………5分.
(2)∵与的党员人数的比值为2:3,
采用分层随机抽样方法抽取5人,则在中抽取2人,中抽3人,
设抽取人的编号为,,抽取人的编号为,,,…………7分
则从5人中任选2人进行问卷调查对应的样本空间为:
,,,,,,,,,,共10个样本点, ………………9分
这2人中至少有1人成绩低于76分的有:
,,,,,,,共7个样本点,11分
故这2人中至少有1人成绩低于76分的概率.………………………………12分
20. (Ⅰ)证明:∵ △是等腰直角三角形,,点为的中点,
∴ . ………………………………………1分
∵ 平面平面,平面∩平面,平面,
∴ 平面.………………………………2分
∵ 平面,
∴ ∥.………………………………………3分
∵ 平面,平面,
∴ ∥平面.………………………………4分
(Ⅱ)解法1:由(Ⅰ)知∥平面,
∴ 点到平面的距离等于点到平面的距离.
过作,垂足为点,
∵ 平面,平面,
∴ . ………………………………………6分
∵ 平面,平面,,
∴ 平面. ………………………………………7分
∵ ,△是等边三角形,
∴ ,,.………………………………9分
∴ ………………………………………10分
.
∴ 三棱锥的体积为. …………12分
解法2: 由(Ⅰ)知∥平面,
∴ 点到平面的距离等于点到平面的距离. …………………5分
∵ ,△是等边三角形,
∴ ,. ………………………………………6分
连接, 则, . ……………………………7分
∴ ………………………………………10分
.
∴ 三棱锥的体积为. ………………………………………12分
21. 解:(1)
3分
∴的最小正周期. …………………………4分
由得
∴的单调递增区间为 ……6分
(2)
∴函数在区间上的值域为
(3)由,由为锐角,得.……………………8分
由余弦定理,得.……10分
∴,当且仅当时等号成立.…………………………………………11分
∴.∴面积的最大值为. ……12分
22.【详解】(1)依题意函数是定义在[,1]上的奇函数,所以,,所以,经检验,该函数为奇函数.…………………3分
(2)在上递增,证明如下:任取,
,…………6分
其中,所以,
故在上递增.……………………………………………………7分
(3)由于对任意的,总存在,使得成立,所以.……………8分
.……………………………………9分
当时,在上递增,,所以.………10分
当时,在上递减,,所以.……………11分
综上所述,.…………………12分
第5页
同课章节目录
