4.8.3平行线的性质导学案

丽星中学七年级数学导学案设计 主备人： 王林芳 小组负责人： 小组长： 2012年7月30日 16:02:25
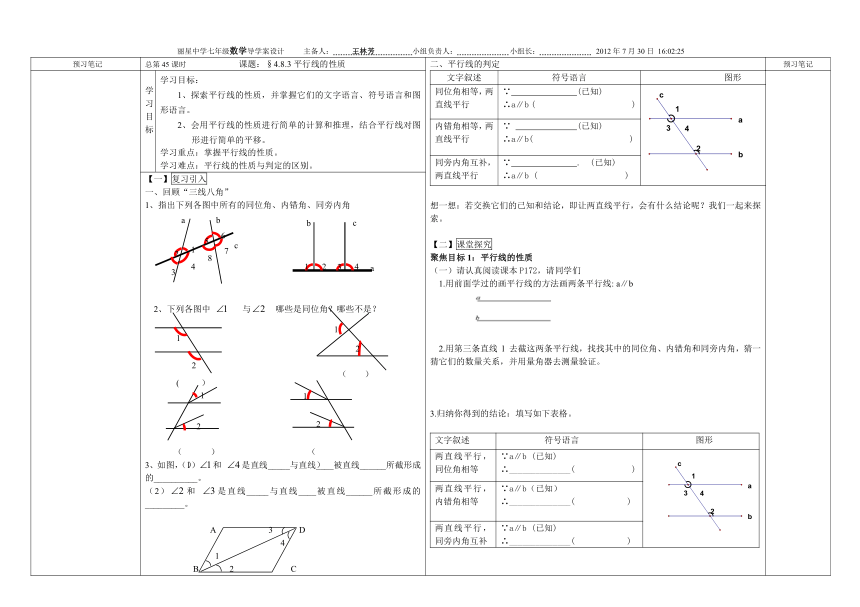
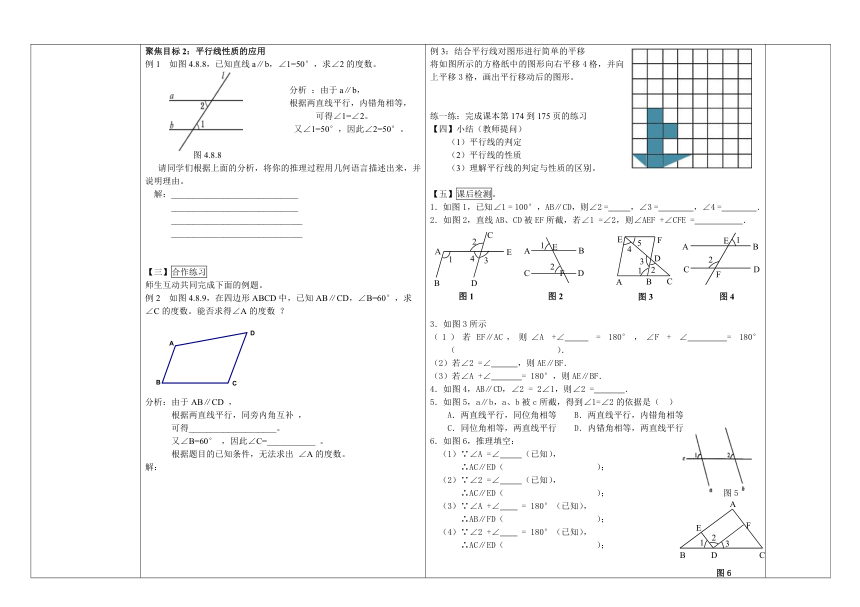
预习笔记 总第45课时 课题：§4.8.3平行线的性质 平行线的判定文字叙述符号语言图形同位角相等，两直线平行∵ (已知)∴a∥b ( )内错角相等，两直线平行∵ (已知)∴a∥b( )同旁内角互补，两直线平行∵ . (已知)∴a∥b ( ) 想一想：若交换它们的已知和结论，即让两直线平行，会有什么结论呢？我们一起来探索。【二】课堂探究聚焦目标1：平行线的性质（一）请认真阅读课本P172，请同学们 1.用前面学过的画平行线的方法画两条平行线: a∥b 2.用第三条直线 l 去截这两条平行线，找找其中的同位角、内错角和同旁内角，猜一猜它们的数量关系，并用量角器去测量验证。3.归纳你得到的结论：填写如下表格。文字叙述符号语言图形两直线平行，同位角相等∵a∥b (已知)∴______________( )两直线平行，内错角相等∵a∥b（已知）∴______________( )两直线平行，同旁内角互补∵a∥b (已知)∴______________( ) 例3：结合平行线对图形进行简单的平移将如图所示的方格纸中的图形向右平移4格，并向上平移3格，画出平行移动后的图形。练一练：完成课本第174到175页的练习【四】小结（教师提问）（1）平行线的判定（2）平行线的性质 （3）理解平行线的判定与性质的区别。【五】课后检测。1．如图1，已知∠1 = 100°，AB∥CD，则∠2 = ，∠3 = ，∠4 = ．2．如图2，直线AB、CD被EF所截，若∠1 =∠2，则∠AEF +∠CFE = ．3．如图3所示（1）若EF∥AC，则∠A +∠ = 180°，∠F + ∠ = 180°（ ）．（2）若∠2 =∠ ，则AE∥BF．（3）若∠A +∠ = 180°，则AE∥BF．4．如图4，AB∥CD，∠2 = 2∠1，则∠2 = ．5．如图5，a∥b，a、b被c所截，得到∠1=∠2的依据是（ ） A．两直线平行，同位角相等 B．两直线平行，内错角相等C．同位角相等，两直线平行 D．内错角相等，两直线平行6．如图6，推理填空： （1）∵∠A =∠ （已知）， ∴AC∥ED（ ）； （2）∵∠2 =∠ （已知）， ∴AC∥ED（ ）； 图5（3）∵∠A +∠ = 180°（已知）， ∴AB∥FD（ ）；（4）∵∠2 +∠ = 180°（已知）， ∴AC∥ED（ ）； 预习笔记
学习目标 学习目标： 1、探索平行线的性质，并掌握它们的文字语言、符号语言和图形语言。 2、会用平行线的性质进行简单的计算和推理，结合平行线对图形进行简单的平移。学习重点：掌握平行线的性质。学习难点：平行线的性质与判定的区别。
【一】复习引入回顾“三线八角”指出下列各图中所有的同位角、内错角、同旁内角 2、下列各图中 与 哪些是同位角？哪些不是？ ）3、如图，（1）和 是直线_____与直线____被直线______所截形成的__________。（2）和 是直线_____与直线____被直线______所截形成的_________。 A 3 D 4 1 B 2 C聚焦目标2：平行线性质的应用例1 如图4.8.8，已知直线a∥b，∠1=50°，求∠2的度数。 分析 ：由于a∥b， 根据两直线平行，内错角相等， 可得∠1=∠2。 又∠1=50°，因此∠2=50°。 图4.8.8 请同学们根据上面的分析，将你的推理过程用几何语言描述出来，并说明理由。 解：_____________________________ _____________________________ ______________________________ ______________________________【三】合作练习 师生互动共同完成下面的例题。例2 如图4.8.9，在四边形ABCD中，已知AB∥CD，∠B=60°，求∠C的度数。能否求得∠A的度数 ？ 分析：由于AB∥CD ， 根据两直线平行，同旁内角互补 ， 可得____________________。 又∠B=60° ，因此∠C=___________ 。 根据题目的已知条件，无法求出 ∠A的度数。 解：
图1
2
4
3
1
A
B
C
D
E
1
2
A
B
D
C
E
F
图2
1
2
3
4
5
A
B
C
D
F
E
图3
1
2
A
B
C
D
E
F
图4
1
2
3
A
F
C
D
B
E
图6
a
b
c
8
4
3
2
1
7
6
5
b
c
a
1
4
3
2
1
2
（ ）
1
2
( ）
（ ）
1
2
（ ）
1
2