4.9.1图形的初步认识复习一导学案
文档属性
| 名称 | 4.9.1图形的初步认识复习一导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 46.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-06 12:44:48 | ||
图片预览



文档简介
丽星中学八年级数学导学案设计 主备人: 娄伟涛 小组负责人: 小组长: 2012年7月30日 16:05:57
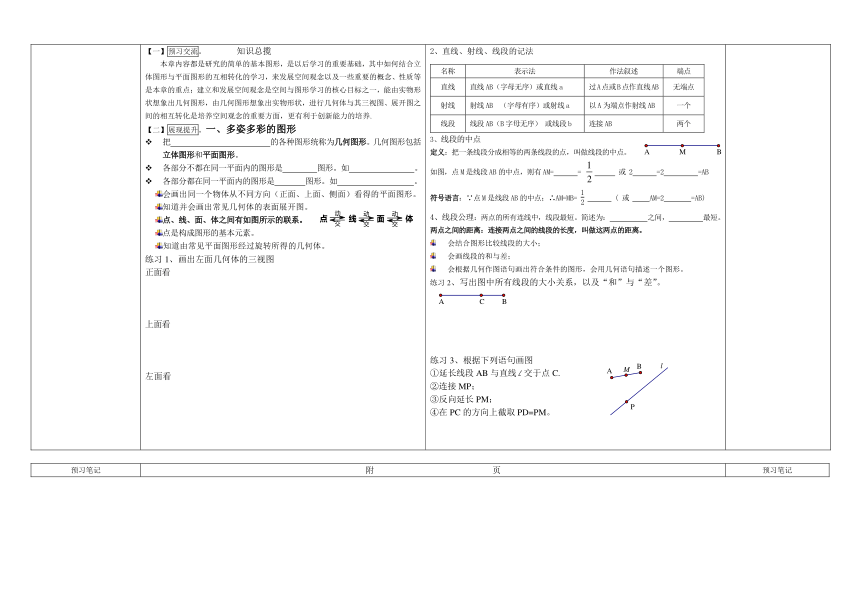
预习笔记 总第46课时 课题:图形的初步认识 复习 二、直线、射线、线段1、直线公理:经过两点有一条直线, 一条直线。简述为: 。两条不同的直线有一个 时,就称两条直线相交,这个公共点叫它们的 。射线和线段都是直线的一部分。2、直线、射线、线段的记法名称表示法作法叙述端点直线直线AB(字母无序)或直线a过A点或B点作直线AB无端点射线射线AB (字母有序)或射线a以A为端点作射线AB一个线段线段AB(B字母无序) 或线段b连接AB两个3、线段的中点定义:把一条线段分成相等的两条线段的点,叫做线段的中点。如图,点M是线段AB的中点,则有AM= = 或 2 =2 =AB符号语言:∵点M是线段AB的中点;∴AM=MB= ( 或 AM=2 =AB)4、线段公理:两点的所有连线中,线段最短。简述为: 之间, 最短。两点之间的距离:连接两点之间的线段的长度,叫做这两点的距离。会结合图形比较线段的大小;会画线段的和与差;会根据几何作图语句画出符合条件的图形,会用几何语句描述一个图形。练习2、写出图中所有线段的大小关系,以及“和”与“差”。练习3、根据下列语句画图①延长线段AB与直线L交于点C.②连接MP;③反向延长PM;④在PC的方向上截取PD=PM。 预习笔记
学习目标 1、加深对物体的形状的认识,并从感性逐步上升到抽象的几何图形,并通过从不同方向看立体图形和展开立体图形,初步认识立体图形与平面图形的联系;2、进一步认识角,以及角的表示方法,角的度量,角的画法.角的比较,补角和余角等内容.会进行线段或角的比较,能估计一个角的大小,会进行角的单位的简单换算.3、能区分直线、射线、线段的概念,并体会它们的一些性质,结合生活情景认识角并知道周角、平角等概念.
【一】预习交流。 知识总揽本章内容都是研究的简单的基本图形,是以后学习的重要基础,其中如何结合立体图形与平面图形的互相转化的学习,来发展空间观念以及一些重要的概念、性质等是本章的重点;建立和发展空间观念是空间与图形学习的核心目标之一,能由实物形状想象出几何图形,由几何图形想象出实物形状,进行几何体与其三视图、展开图之间的相互转化是培养空间观念的重要方面,更有利于创新能力的培养.【二】展现提升。一、多姿多彩的图形把 的各种图形统称为几何图形。几何图形包括立体图形和平面图形。各部分不都在同一平面内的图形是 图形。如 。各部分都在同一平面内的图形是 图形。如 。会画出同一个物体从不同方向(正面、上面、侧面)看得的平面图形。知道并会画出常见几何体的表面展开图。点、线、面、体之间有如图所示的联系。点是构成图形的基本元素。知道由常见平面图形经过旋转所得的几何体。练习1、画出左面几何体的三视图正面看上面看左面看
预习笔记 附 页 预习笔记
三、角的定义静态(从构成上看): 有 的两条 组成的图形叫做角。动态(从形成上看): 由一条射线 而形成的图形叫做角。1、角的表示方法(1)用三个英文大写字母表示任意一个角;(2)用一个英文大写字母表示一个独立的角(顶点处只有一个角);(3)加弧线、标数字表示一个角;(4)加弧线、标小写希腊字母(如:α,β)表示一个角。2、角的度量 (1)1个周角=2个平角=4个直角=360° (2)1°=60′=3600″(3)用一副三角尺能画的角都是15°的整数倍。3、角的平分线定义:从一个角的 出发,把这个角分成 的两个角的 ,叫做这个角的平分线。如图,射线OB是∠AOC的平分线,则有∠AOB=∠BOC= ∠AOC 或 2∠AOB=2∠COB=∠AOC 用符号语言表示:∵OB平分 ∴∠AOB=∠ = ∠ (或 2∠ =2∠ =∠AOC)4、角的比较与运算会结合图形比较角的大小;会进行角度运算。5、互余、互补互余:如果两个角的和为90 ,那么这两个角互为余角。52°9′36″的余角是 。互补:如果两个角的和为180 ,那么这两个角互为补角。52°9′36″的补角是 。互为余角的性质:同角的余角相等;等角的余角相等。互为余角的性质:同角的余角相等;等角的余角相等。6、方向角(用角度表示方向)一般以正北、正南为基准,用向东或向西旋转的角度表示方向。如图所示,OA方向可表示为北偏西60 。如:西南方向——南偏西450。练习4、练习5、写出图中所有角的大小关系, 以及它们的和与差。 练习5·填空·计算 步骤可以写到预习笔记栏①用度、分、秒表示37.26°= 。②用度表示52°9′36″= 。③45°19′28″+26°40′32″ ④ 98°18′-56. 5° ⑥36°15′27″×3 ⑦27°47′×3+108°30′÷6四、相交线、平行线 1.垂线: 垂线段最短。 叫做点到直线的距离;2.过一点(直线上或直线外) 直线和已知直线垂直;3.会过一点画(作)已知直线的垂线;(一落,二靠,三画)4.直线公理:过直线外一点, 直线与已知直线平行;5.直线公理的推论: 6.三线八角与平行线的关系;①判定公理: ,两直线平行. ∵ ∠1=∠2, ∴ a∥b.②判定定理1: ,两直线平行. ∵ ∠1=∠2, ∴ a∥b.③判定定理2: ,两直线平行. ∵∠1+∠2=1800 , ∴ a∥b. ④性质公理: 两直线平行, . ∵ a∥b, ∴∠1=∠2.⑤性质定理1:两直线平行, . ∵ a∥b, ∴∠1=∠2.⑥性质定理2:两直线平行, . ∵ a∥b, ∴ ∠1+∠2=1800 . 7.平行线之间的距离; 8.会过直线外一点,画已知直线的平行线.练习6、如图,已知∠C=∠AOC,OC平分∠AOD,OC⊥OE,∠D=54°.求∠C、∠BOE的度数.
类似的,从一个角的顶点出发,把这个角分成相等的n个角的射线,叫做这个角
的 。
类似的,把线段分成相等的三条线段的点,叫线段的 。
把线段分成相等的n条线段的点,叫线段的 。
这是你应该会的,你掌握了吗?
预习笔记 总第46课时 课题:图形的初步认识 复习 二、直线、射线、线段1、直线公理:经过两点有一条直线, 一条直线。简述为: 。两条不同的直线有一个 时,就称两条直线相交,这个公共点叫它们的 。射线和线段都是直线的一部分。2、直线、射线、线段的记法名称表示法作法叙述端点直线直线AB(字母无序)或直线a过A点或B点作直线AB无端点射线射线AB (字母有序)或射线a以A为端点作射线AB一个线段线段AB(B字母无序) 或线段b连接AB两个3、线段的中点定义:把一条线段分成相等的两条线段的点,叫做线段的中点。如图,点M是线段AB的中点,则有AM= = 或 2 =2 =AB符号语言:∵点M是线段AB的中点;∴AM=MB= ( 或 AM=2 =AB)4、线段公理:两点的所有连线中,线段最短。简述为: 之间, 最短。两点之间的距离:连接两点之间的线段的长度,叫做这两点的距离。会结合图形比较线段的大小;会画线段的和与差;会根据几何作图语句画出符合条件的图形,会用几何语句描述一个图形。练习2、写出图中所有线段的大小关系,以及“和”与“差”。练习3、根据下列语句画图①延长线段AB与直线L交于点C.②连接MP;③反向延长PM;④在PC的方向上截取PD=PM。 预习笔记
学习目标 1、加深对物体的形状的认识,并从感性逐步上升到抽象的几何图形,并通过从不同方向看立体图形和展开立体图形,初步认识立体图形与平面图形的联系;2、进一步认识角,以及角的表示方法,角的度量,角的画法.角的比较,补角和余角等内容.会进行线段或角的比较,能估计一个角的大小,会进行角的单位的简单换算.3、能区分直线、射线、线段的概念,并体会它们的一些性质,结合生活情景认识角并知道周角、平角等概念.
【一】预习交流。 知识总揽本章内容都是研究的简单的基本图形,是以后学习的重要基础,其中如何结合立体图形与平面图形的互相转化的学习,来发展空间观念以及一些重要的概念、性质等是本章的重点;建立和发展空间观念是空间与图形学习的核心目标之一,能由实物形状想象出几何图形,由几何图形想象出实物形状,进行几何体与其三视图、展开图之间的相互转化是培养空间观念的重要方面,更有利于创新能力的培养.【二】展现提升。一、多姿多彩的图形把 的各种图形统称为几何图形。几何图形包括立体图形和平面图形。各部分不都在同一平面内的图形是 图形。如 。各部分都在同一平面内的图形是 图形。如 。会画出同一个物体从不同方向(正面、上面、侧面)看得的平面图形。知道并会画出常见几何体的表面展开图。点、线、面、体之间有如图所示的联系。点是构成图形的基本元素。知道由常见平面图形经过旋转所得的几何体。练习1、画出左面几何体的三视图正面看上面看左面看
预习笔记 附 页 预习笔记
三、角的定义静态(从构成上看): 有 的两条 组成的图形叫做角。动态(从形成上看): 由一条射线 而形成的图形叫做角。1、角的表示方法(1)用三个英文大写字母表示任意一个角;(2)用一个英文大写字母表示一个独立的角(顶点处只有一个角);(3)加弧线、标数字表示一个角;(4)加弧线、标小写希腊字母(如:α,β)表示一个角。2、角的度量 (1)1个周角=2个平角=4个直角=360° (2)1°=60′=3600″(3)用一副三角尺能画的角都是15°的整数倍。3、角的平分线定义:从一个角的 出发,把这个角分成 的两个角的 ,叫做这个角的平分线。如图,射线OB是∠AOC的平分线,则有∠AOB=∠BOC= ∠AOC 或 2∠AOB=2∠COB=∠AOC 用符号语言表示:∵OB平分 ∴∠AOB=∠ = ∠ (或 2∠ =2∠ =∠AOC)4、角的比较与运算会结合图形比较角的大小;会进行角度运算。5、互余、互补互余:如果两个角的和为90 ,那么这两个角互为余角。52°9′36″的余角是 。互补:如果两个角的和为180 ,那么这两个角互为补角。52°9′36″的补角是 。互为余角的性质:同角的余角相等;等角的余角相等。互为余角的性质:同角的余角相等;等角的余角相等。6、方向角(用角度表示方向)一般以正北、正南为基准,用向东或向西旋转的角度表示方向。如图所示,OA方向可表示为北偏西60 。如:西南方向——南偏西450。练习4、练习5、写出图中所有角的大小关系, 以及它们的和与差。 练习5·填空·计算 步骤可以写到预习笔记栏①用度、分、秒表示37.26°= 。②用度表示52°9′36″= 。③45°19′28″+26°40′32″ ④ 98°18′-56. 5° ⑥36°15′27″×3 ⑦27°47′×3+108°30′÷6四、相交线、平行线 1.垂线: 垂线段最短。 叫做点到直线的距离;2.过一点(直线上或直线外) 直线和已知直线垂直;3.会过一点画(作)已知直线的垂线;(一落,二靠,三画)4.直线公理:过直线外一点, 直线与已知直线平行;5.直线公理的推论: 6.三线八角与平行线的关系;①判定公理: ,两直线平行. ∵ ∠1=∠2, ∴ a∥b.②判定定理1: ,两直线平行. ∵ ∠1=∠2, ∴ a∥b.③判定定理2: ,两直线平行. ∵∠1+∠2=1800 , ∴ a∥b. ④性质公理: 两直线平行, . ∵ a∥b, ∴∠1=∠2.⑤性质定理1:两直线平行, . ∵ a∥b, ∴∠1=∠2.⑥性质定理2:两直线平行, . ∵ a∥b, ∴ ∠1+∠2=1800 . 7.平行线之间的距离; 8.会过直线外一点,画已知直线的平行线.练习6、如图,已知∠C=∠AOC,OC平分∠AOD,OC⊥OE,∠D=54°.求∠C、∠BOE的度数.
类似的,从一个角的顶点出发,把这个角分成相等的n个角的射线,叫做这个角
的 。
类似的,把线段分成相等的三条线段的点,叫线段的 。
把线段分成相等的n条线段的点,叫线段的 。
这是你应该会的,你掌握了吗?
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
