1.2.4 第1课时 绝对值-2021-2022学年人教版数学七年级上册知识点整理与同步练习(Word版含答案)
文档属性
| 名称 | 1.2.4 第1课时 绝对值-2021-2022学年人教版数学七年级上册知识点整理与同步练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 20:32:30 | ||
图片预览


文档简介
第1章 有理数
绝对值的意义
1、 定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a | . (这里的数a可以是正数、负数和0).
2、强调
由绝对值的定义可知:一个数对应的点离原点越近,它的绝对值越小,离原点越远,它的绝对值越大,所以没有绝对值最大的数,只有绝对值最小的数为0.
绝对值的性质
1、几何定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a |
2、代数定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;任意一个数的绝对值为唯一非负数.
用式子表示为:
3、强调
绝对值的非负性是绝对值的一个重要性质,即对于任意有理数a,都有| a | ≥ 0.
4、互为相反数的两个数的绝对值相等.
一.选择题(共10小题)
1.计算|﹣6|的结果等于( )
A.6 B.﹣6 C. D.
2.﹣10的绝对值是( )
A. B. C.﹣10 D.10
3.如果|x﹣2|=2﹣x,那么x的取值范围是( )
A.x≤2 B.x<2 C.x≥2 D.x>2
4.如图是小竹观察到温度计的示数,该示数的绝对值是( )
A.﹣9 B.9 C.﹣11 D.11
5.数轴上表示数m和m+2的点到原点的距离相等,则m为( )
A.﹣2 B.2 C.1 D.﹣1
6.以下各数中绝对值最小的数是( )
A.0 B.﹣0.5 C.1 D.﹣2
7.若不为零的有理数a满足|a|=﹣a,则a的值可以是( )
A.6 B.4 C.2 D.﹣2
8.下列各式不成立的是( )
A.|﹣2|=2 B.|+2|=|﹣2| C.﹣|﹣3|=﹣3 D.﹣|2|=|﹣2|
9.比赛用的乒乓球的质量有严格的规定,但实际生产的乒乓球的质量可能会有一些偏差.以下检验记录(“+”表示超出标准质量,“﹣”表示不足标准质量)中,质量最接近标准质量乒乓球是( )
编号 1 2 3 4
偏差/g +0.01 ﹣0.02 ﹣0.03 +0.04
A.1号 B.2号 C.3号 D.4号
10.若ab≠0,那么的取值不可能是( )
A.﹣2 B.0 C.1 D.2
二.填空题(共4小题)
11.若|x+2|=3,则x是 .
12.﹣1的绝对值是 .
13.2021的绝对值是 .
14.若a与1互为相反数,则|a+1|= .
三.解答题(共3小题)
15.已知a是2的相反数,计算|a﹣2|的值.
16.计算:已知|x|=3,|y|=2,
(1)当xy<0时,求x+y的值;
(2)求x﹣y的最大值.
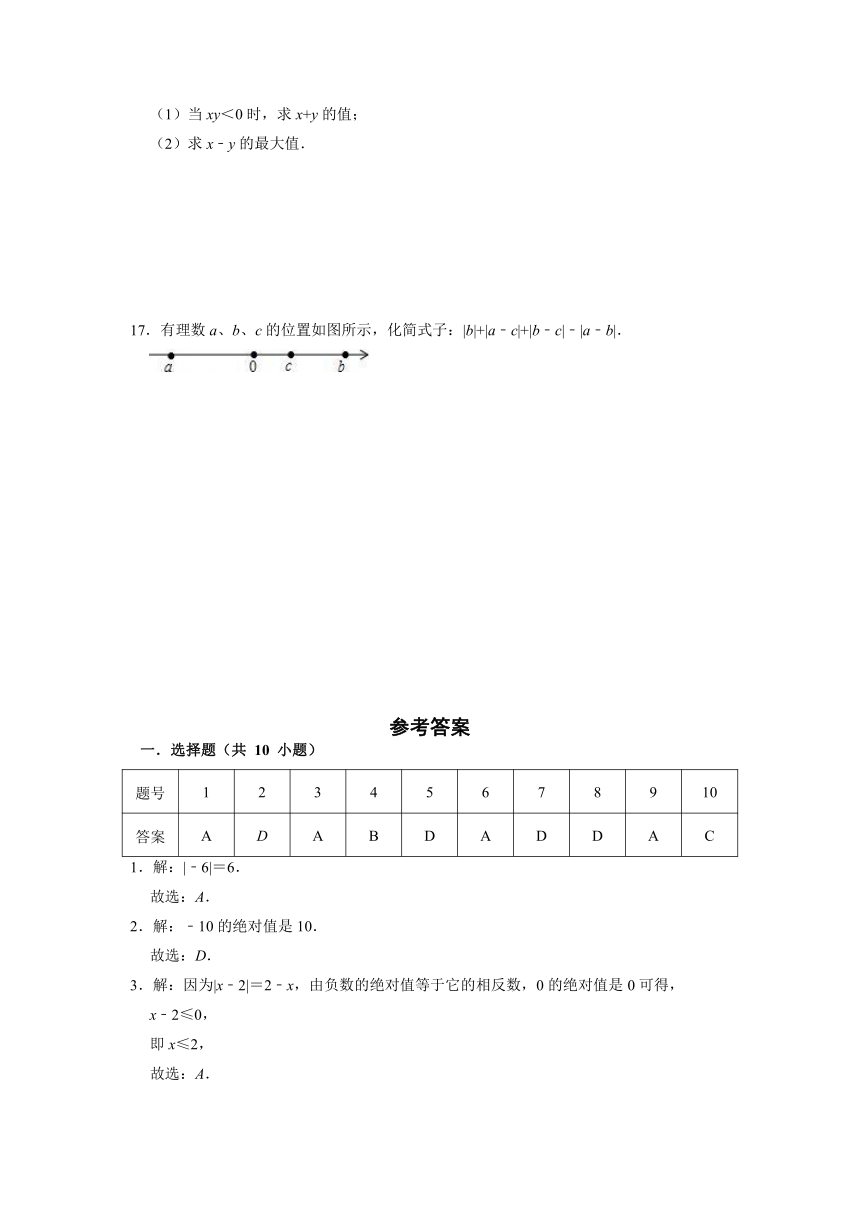
17.有理数a、b、c的位置如图所示,化简式子:|b|+|a﹣c|+|b﹣c|﹣|a﹣b|.
参考答案
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B D A D D A C
1.解:|﹣6|=6.
故选:A.
2.解:﹣10的绝对值是10.
故选:D.
3.解:因为|x﹣2|=2﹣x,由负数的绝对值等于它的相反数,0的绝对值是0可得,
x﹣2≤0,
即x≤2,
故选:A.
4.解:观察温度计,这个示数为﹣9,
所以该示数的绝对值为9,
故选:B.
5.解:由题意得:|m|=|m+2|,
∴m=m+2或m=﹣(m+2),
∴m=﹣1.
故选:D.
6.解:∵|0|=0,|﹣0.5|=0.5,|1|=1,|﹣2|=2,
∴|0|<|﹣0.5|<|1|<|﹣2|,
∴各选项中绝对值最小的数是0.
故选:A.
7.解:∵|a|=﹣a,a≠0,
∴a<0.
故选:D.
8.解:A.∵2正确,
故A选项成立,不符合题目要求;
B.∵正确,
故B选项成立,不符合题目要求;
C.∵3正确,
故C选项成立,不符合题目要求;
D.∵错误,
∴D选项不成立,符合题目要求;
故选:D.
9.解:|+0.01|=0.01,|﹣0.02|=0.02,|﹣0.03|=0.03,|+0.04|=0.04,
0.04>0.03>0.02>0.01,
绝对值越小越接近标准.
所以最接近标准质量是1号乒乓球.
故选:A.
10.解:∵ab≠0,
∴有四种情况:①a>0,b>0,②a<0,b<0,③a>0,b<0,④a<0,b>0;
①当a>0,b>0时,
1+1=2;
②当a<0,b<0时,
1﹣1=﹣2;
③当a>0,b<0时,
1﹣1=0;
④当a<0,b>0时,
1+1=0;
综上所述,的值为:±2或0.
故选:C.
二.填空题(共4小题)
11.解:∵|x+2|=3,
∴x+2=±3,
当x+2=3时,x=1;
当x+2=﹣3时,x=﹣5;
综上,x的值为1或﹣5.
故答案为:1或﹣5.
12.解:﹣1的绝对值是1,
故答案为:1.
13.解:2021的绝对值即为:|2021|=2021.
故答案为:2021.
14.解:∵a与1互为相反数,
∴a+1=0,
∴|a+1|=0,
故答案为:0.
三.解答题(共3小题)
15.解:∵a是2的相反数,
∴a=﹣2,
∴|a﹣2|=4.
16.解:由题意知:x=±3,y=±2,
(1)∵xy<0,
∴x=3,y=﹣2或x=﹣3,y=2,
∴x+y=±1,
(2)当x=3,y=2时,x﹣y=3﹣2=1;
当x=3,y=﹣2时,x﹣y=3﹣(﹣2)=5;
当x=﹣3,y=2时,x﹣y=﹣3﹣2=﹣5;
当x=﹣3,y=﹣2时,x﹣y=﹣3﹣(﹣2)=﹣1,
所以x﹣y的最大值是5
17.解:由数轴可得:b>0,a﹣c<0,b﹣c>0,a﹣b<0,
故:|b|+|a﹣c|+|b﹣c|﹣|a﹣b|
=b+c﹣a+b﹣c﹣(b﹣a)
=b.
绝对值的意义
1、 定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a | . (这里的数a可以是正数、负数和0).
2、强调
由绝对值的定义可知:一个数对应的点离原点越近,它的绝对值越小,离原点越远,它的绝对值越大,所以没有绝对值最大的数,只有绝对值最小的数为0.
绝对值的性质
1、几何定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a |
2、代数定义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0;任意一个数的绝对值为唯一非负数.
用式子表示为:
3、强调
绝对值的非负性是绝对值的一个重要性质,即对于任意有理数a,都有| a | ≥ 0.
4、互为相反数的两个数的绝对值相等.
一.选择题(共10小题)
1.计算|﹣6|的结果等于( )
A.6 B.﹣6 C. D.
2.﹣10的绝对值是( )
A. B. C.﹣10 D.10
3.如果|x﹣2|=2﹣x,那么x的取值范围是( )
A.x≤2 B.x<2 C.x≥2 D.x>2
4.如图是小竹观察到温度计的示数,该示数的绝对值是( )
A.﹣9 B.9 C.﹣11 D.11
5.数轴上表示数m和m+2的点到原点的距离相等,则m为( )
A.﹣2 B.2 C.1 D.﹣1
6.以下各数中绝对值最小的数是( )
A.0 B.﹣0.5 C.1 D.﹣2
7.若不为零的有理数a满足|a|=﹣a,则a的值可以是( )
A.6 B.4 C.2 D.﹣2
8.下列各式不成立的是( )
A.|﹣2|=2 B.|+2|=|﹣2| C.﹣|﹣3|=﹣3 D.﹣|2|=|﹣2|
9.比赛用的乒乓球的质量有严格的规定,但实际生产的乒乓球的质量可能会有一些偏差.以下检验记录(“+”表示超出标准质量,“﹣”表示不足标准质量)中,质量最接近标准质量乒乓球是( )
编号 1 2 3 4
偏差/g +0.01 ﹣0.02 ﹣0.03 +0.04
A.1号 B.2号 C.3号 D.4号
10.若ab≠0,那么的取值不可能是( )
A.﹣2 B.0 C.1 D.2
二.填空题(共4小题)
11.若|x+2|=3,则x是 .
12.﹣1的绝对值是 .
13.2021的绝对值是 .
14.若a与1互为相反数,则|a+1|= .
三.解答题(共3小题)
15.已知a是2的相反数,计算|a﹣2|的值.
16.计算:已知|x|=3,|y|=2,
(1)当xy<0时,求x+y的值;
(2)求x﹣y的最大值.
17.有理数a、b、c的位置如图所示,化简式子:|b|+|a﹣c|+|b﹣c|﹣|a﹣b|.
参考答案
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B D A D D A C
1.解:|﹣6|=6.
故选:A.
2.解:﹣10的绝对值是10.
故选:D.
3.解:因为|x﹣2|=2﹣x,由负数的绝对值等于它的相反数,0的绝对值是0可得,
x﹣2≤0,
即x≤2,
故选:A.
4.解:观察温度计,这个示数为﹣9,
所以该示数的绝对值为9,
故选:B.
5.解:由题意得:|m|=|m+2|,
∴m=m+2或m=﹣(m+2),
∴m=﹣1.
故选:D.
6.解:∵|0|=0,|﹣0.5|=0.5,|1|=1,|﹣2|=2,
∴|0|<|﹣0.5|<|1|<|﹣2|,
∴各选项中绝对值最小的数是0.
故选:A.
7.解:∵|a|=﹣a,a≠0,
∴a<0.
故选:D.
8.解:A.∵2正确,
故A选项成立,不符合题目要求;
B.∵正确,
故B选项成立,不符合题目要求;
C.∵3正确,
故C选项成立,不符合题目要求;
D.∵错误,
∴D选项不成立,符合题目要求;
故选:D.
9.解:|+0.01|=0.01,|﹣0.02|=0.02,|﹣0.03|=0.03,|+0.04|=0.04,
0.04>0.03>0.02>0.01,
绝对值越小越接近标准.
所以最接近标准质量是1号乒乓球.
故选:A.
10.解:∵ab≠0,
∴有四种情况:①a>0,b>0,②a<0,b<0,③a>0,b<0,④a<0,b>0;
①当a>0,b>0时,
1+1=2;
②当a<0,b<0时,
1﹣1=﹣2;
③当a>0,b<0时,
1﹣1=0;
④当a<0,b>0时,
1+1=0;
综上所述,的值为:±2或0.
故选:C.
二.填空题(共4小题)
11.解:∵|x+2|=3,
∴x+2=±3,
当x+2=3时,x=1;
当x+2=﹣3时,x=﹣5;
综上,x的值为1或﹣5.
故答案为:1或﹣5.
12.解:﹣1的绝对值是1,
故答案为:1.
13.解:2021的绝对值即为:|2021|=2021.
故答案为:2021.
14.解:∵a与1互为相反数,
∴a+1=0,
∴|a+1|=0,
故答案为:0.
三.解答题(共3小题)
15.解:∵a是2的相反数,
∴a=﹣2,
∴|a﹣2|=4.
16.解:由题意知:x=±3,y=±2,
(1)∵xy<0,
∴x=3,y=﹣2或x=﹣3,y=2,
∴x+y=±1,
(2)当x=3,y=2时,x﹣y=3﹣2=1;
当x=3,y=﹣2时,x﹣y=3﹣(﹣2)=5;
当x=﹣3,y=2时,x﹣y=﹣3﹣2=﹣5;
当x=﹣3,y=﹣2时,x﹣y=﹣3﹣(﹣2)=﹣1,
所以x﹣y的最大值是5
17.解:由数轴可得:b>0,a﹣c<0,b﹣c>0,a﹣b<0,
故:|b|+|a﹣c|+|b﹣c|﹣|a﹣b|
=b+c﹣a+b﹣c﹣(b﹣a)
=b.
