2021-2022学年鲁教版 数学八年级上册4.1 图形的平移 (2)课件(16张)
文档属性
| 名称 | 2021-2022学年鲁教版 数学八年级上册4.1 图形的平移 (2)课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 732.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 09:07:12 | ||
图片预览





文档简介
(共16张PPT)
第四章 图形的平移与旋转
1 图形的平移(2)
平移的性质:
对应点所连的线段平行(或在同一条直线上)且相等;
对应线段平行(或在同一条直线上)且相等,对应角相等.
【注意】1.决定平移的因素是平移的方向和距离;
2.平移只改变图形的位置,图形的形状和大小不变.
知识回顾
能作出一个图平移后的图形
重点:作平移后的图形
难点:作图时确定图形的对应点
重难点:
学习目标
动手操作:
如图,每个小方格都是边长为1个单位长度的小正方形。将△ABC向右平移3个单位长度,画出平移后的△A1B1C1.
思考:
1.若上题中没有给出平移方向或平移距离,你能作出平移后的△A1B1C1吗?
2.若要画出已知图形平移后的图形,需要知道那几个条件?
A
B
1.点的平移作法
将A点沿着射线XY方向平移3cm.
X
Y
【作法】
1.过点A作射线AZ∥XY;
2.在射线AZ上截取线段AB,使AB=3cm;
3.B点即为所求作.
3cm
Z
简单的平移作图
自主学习
A
C
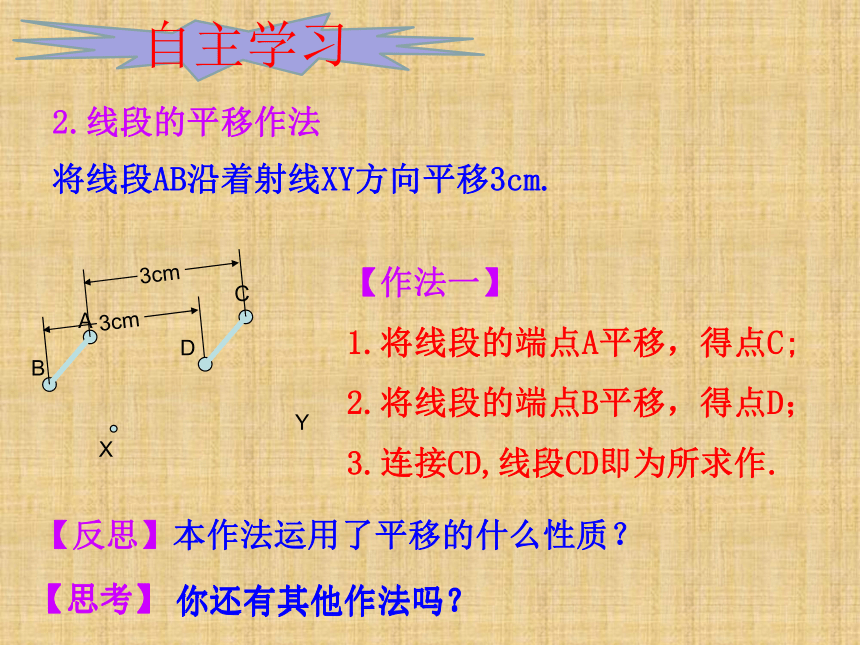
2.线段的平移作法
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法一】
1.将线段的端点A平移,得点C;
2.将线段的端点B平移,得点D;
3.连接CD,线段CD即为所求作.
3cm
B
3cm
D
【反思】本作法运用了平移的什么性质?
【思考】
你还有其他作法吗?
【思考】
你还有其他作法吗?
自主学习
A
C
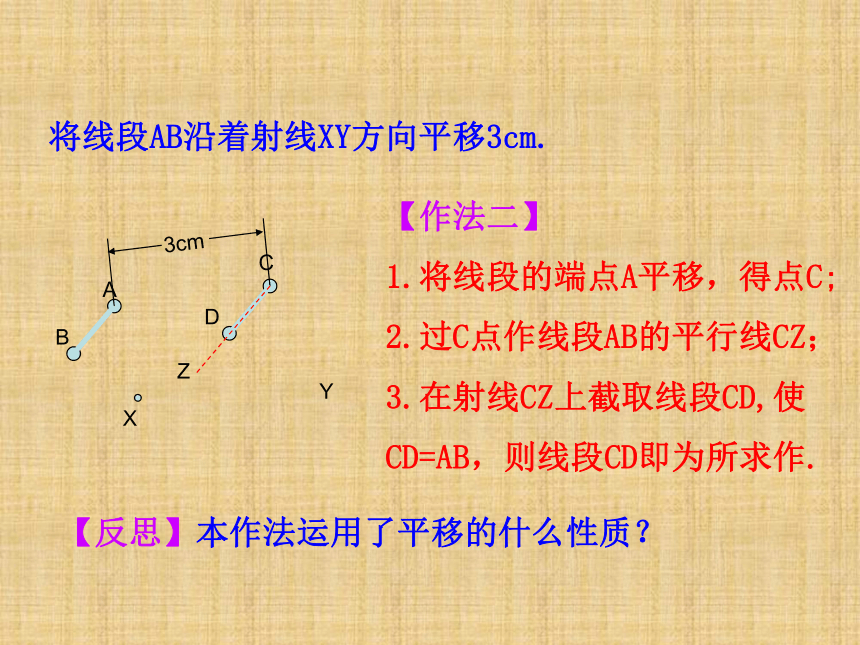
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法二】
1.将线段的端点A平移,得点C;
2.过C点作线段AB的平行线CZ;
3.在射线CZ上截取线段CD,使CD=AB,则线段CD即为所求作.
3cm
B
D
Z
【反思】本作法运用了平移的什么性质?
如图所示,经过平移,线段AB的端点A移到了点D,你能作出线段AB平移后的图形吗?
A
B
D
【解析】
∴线段DE就是线段AB平移后的图形
E
1.连接AD
2.过点B作BE平行
且等于AD
3.连接DE
还有其他作法吗?
对应训练
3.图形的平移作法
如果经过平移,△ABC的顶点A移到了点D.你会作出平移后的三角形吗
【作法】
1.将线段BC沿AD方向平移AD长距离,得线段EF;
2.连接DE, DF;
3.△DEF即为所求作.
B
【反思】本作法运用了平移的什么性质?
C
A
D
E
F
如果经过平移,△ABC的顶点A移到了点D.你会作出平移后的三角形吗 想一想:还有其他作法吗?
B
C
A
D
E
F
M
N
【规律方法】如何进行平移作图
关键在于按要求(方向和距离)作出对应点.
然后,顺次连接对应点即可.
如图,将字母A按箭头所指的方向平移3cm,作出平移后的图形.
【作法】
1. 选择5个控制点;
2. 将5个控制点分别平移;
3. 连接平移后的5个控制点,
得字母A平移后的图形.
3cm
【规律方法】由局部平移实现整体平移.
【反思】本作法运用了平移的什么性质?
对应训练
1.如图,△ABC经过怎样的平移得到△DEF ( )
A.把△ABC向左平移4个单位,再向下平移2个单位
B.把△ABC向右平移4个单位,再向下平移2个单位
C.把△ABC向右平移4个单位,再向上平移2个单位
D.把△ABC向左平移4个单位,再向上平移2个单位
C
2.下列运动属于平移的是( )
A.空中放飞的风筝
B.飞机在跑道上滑行到停止的运动
C.球被运动员投出并进入篮筐的过程
D.乒乓球比赛中高抛发球后乒乓球的运动
3.图①所示的图案通过平移后可以得到的图案是( )
4.(3分)在图形的平移中,下列说法错误的是( )
A.图形上任意点移动的方向相同
B.图形上任意点移动的距离相同
C.图形上可能存在不动点
D.图形上任意两点的连线大小不变
B
A
C
5.如图所示,△DEF是△ABC沿水平方向向右平移后的对
应图形,若∠B=31°,∠C=79°,则∠D的度数是____度.
6.若△ABC经过平移后得到△DEF,∠A=41°,∠C=32°,
EF=3 cm,则∠E=__ ,BC=____cm.
7.如果△ABC沿着北偏东35°的方向移动了6 cm,那么
△ABC的一条角平分线AD上的中点Q向 °方向移动
了6 cm.
8.如图①,两个等边△ABD,△CBD的边长均为1,
将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图②,
则阴影部分的周长为 .
70
107°
3
北偏东35
2
9.平移△ABC,使得边AB移到DE的位置。
下面是小刚的作业,他的做法完全正确,可由于不小心将一团墨汁沾染了作业本,请设法帮小刚补全平移前后的△ABC和△DEF.
拼搏创造奇迹
努力成就未来
再见!
结束语
第四章 图形的平移与旋转
1 图形的平移(2)
平移的性质:
对应点所连的线段平行(或在同一条直线上)且相等;
对应线段平行(或在同一条直线上)且相等,对应角相等.
【注意】1.决定平移的因素是平移的方向和距离;
2.平移只改变图形的位置,图形的形状和大小不变.
知识回顾
能作出一个图平移后的图形
重点:作平移后的图形
难点:作图时确定图形的对应点
重难点:
学习目标
动手操作:
如图,每个小方格都是边长为1个单位长度的小正方形。将△ABC向右平移3个单位长度,画出平移后的△A1B1C1.
思考:
1.若上题中没有给出平移方向或平移距离,你能作出平移后的△A1B1C1吗?
2.若要画出已知图形平移后的图形,需要知道那几个条件?
A
B
1.点的平移作法
将A点沿着射线XY方向平移3cm.
X
Y
【作法】
1.过点A作射线AZ∥XY;
2.在射线AZ上截取线段AB,使AB=3cm;
3.B点即为所求作.
3cm
Z
简单的平移作图
自主学习
A
C
2.线段的平移作法
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法一】
1.将线段的端点A平移,得点C;
2.将线段的端点B平移,得点D;
3.连接CD,线段CD即为所求作.
3cm
B
3cm
D
【反思】本作法运用了平移的什么性质?
【思考】
你还有其他作法吗?
【思考】
你还有其他作法吗?
自主学习
A
C
将线段AB沿着射线XY方向平移3cm.
X
Y
【作法二】
1.将线段的端点A平移,得点C;
2.过C点作线段AB的平行线CZ;
3.在射线CZ上截取线段CD,使CD=AB,则线段CD即为所求作.
3cm
B
D
Z
【反思】本作法运用了平移的什么性质?
如图所示,经过平移,线段AB的端点A移到了点D,你能作出线段AB平移后的图形吗?
A
B
D
【解析】
∴线段DE就是线段AB平移后的图形
E
1.连接AD
2.过点B作BE平行
且等于AD
3.连接DE
还有其他作法吗?
对应训练
3.图形的平移作法
如果经过平移,△ABC的顶点A移到了点D.你会作出平移后的三角形吗
【作法】
1.将线段BC沿AD方向平移AD长距离,得线段EF;
2.连接DE, DF;
3.△DEF即为所求作.
B
【反思】本作法运用了平移的什么性质?
C
A
D
E
F
如果经过平移,△ABC的顶点A移到了点D.你会作出平移后的三角形吗 想一想:还有其他作法吗?
B
C
A
D
E
F
M
N
【规律方法】如何进行平移作图
关键在于按要求(方向和距离)作出对应点.
然后,顺次连接对应点即可.
如图,将字母A按箭头所指的方向平移3cm,作出平移后的图形.
【作法】
1. 选择5个控制点;
2. 将5个控制点分别平移;
3. 连接平移后的5个控制点,
得字母A平移后的图形.
3cm
【规律方法】由局部平移实现整体平移.
【反思】本作法运用了平移的什么性质?
对应训练
1.如图,△ABC经过怎样的平移得到△DEF ( )
A.把△ABC向左平移4个单位,再向下平移2个单位
B.把△ABC向右平移4个单位,再向下平移2个单位
C.把△ABC向右平移4个单位,再向上平移2个单位
D.把△ABC向左平移4个单位,再向上平移2个单位
C
2.下列运动属于平移的是( )
A.空中放飞的风筝
B.飞机在跑道上滑行到停止的运动
C.球被运动员投出并进入篮筐的过程
D.乒乓球比赛中高抛发球后乒乓球的运动
3.图①所示的图案通过平移后可以得到的图案是( )
4.(3分)在图形的平移中,下列说法错误的是( )
A.图形上任意点移动的方向相同
B.图形上任意点移动的距离相同
C.图形上可能存在不动点
D.图形上任意两点的连线大小不变
B
A
C
5.如图所示,△DEF是△ABC沿水平方向向右平移后的对
应图形,若∠B=31°,∠C=79°,则∠D的度数是____度.
6.若△ABC经过平移后得到△DEF,∠A=41°,∠C=32°,
EF=3 cm,则∠E=__ ,BC=____cm.
7.如果△ABC沿着北偏东35°的方向移动了6 cm,那么
△ABC的一条角平分线AD上的中点Q向 °方向移动
了6 cm.
8.如图①,两个等边△ABD,△CBD的边长均为1,
将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图②,
则阴影部分的周长为 .
70
107°
3
北偏东35
2
9.平移△ABC,使得边AB移到DE的位置。
下面是小刚的作业,他的做法完全正确,可由于不小心将一团墨汁沾染了作业本,请设法帮小刚补全平移前后的△ABC和△DEF.
拼搏创造奇迹
努力成就未来
再见!
结束语
