《 组合图形的面积练习》第8课时 (课件) 数学 五年级上册 青岛版(共14张PPT)
文档属性
| 名称 | 《 组合图形的面积练习》第8课时 (课件) 数学 五年级上册 青岛版(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
《组合图形的面积练习》第8课时 课件
学习目标
通过引导回顾整理,加深对组合图形的特征和面积计算方法的理解,进一步理解并掌握求组合图形的面积就是求几个简单平面图形的面积的和或差的计算。
自学指导
认真看课本77、78页信息窗4内容思考:
1.怎样求多边形的面积?
2.求组合图形面积的一般方法有几种?
3分钟后看谁汇报地最好
求组合图形面积的一般方法:
⑴分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
⑵添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
一、问题回顾,再现新知
新图形
学过的图形
割、补、拼
转 化
想一想,怎样求多边形的面积?
一、问题回顾,再现新知
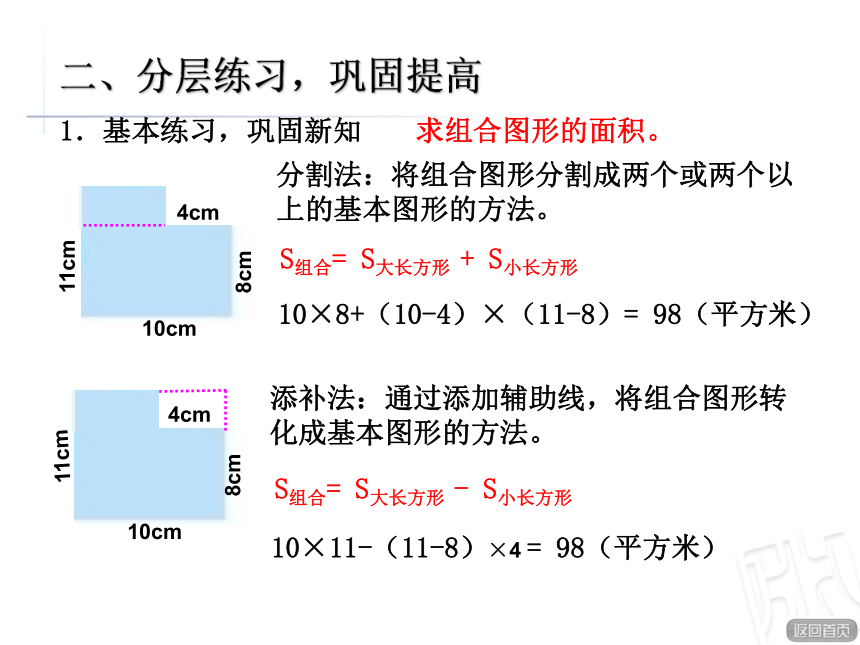
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
1.基本练习,巩固新知 求组合图形的面积。
二、分层练习,巩固提高
10cm
8cm
11cm
4cm
S组合= S大长方形 + S小长方形
10×8+(10-4)×(11-8)= 98(平方米)
10cm
8cm
11cm
4cm
S组合= S大长方形 - S小长方形
10×11-(11-8)×4 = 98(平方米)
二、分层练习,巩固提高
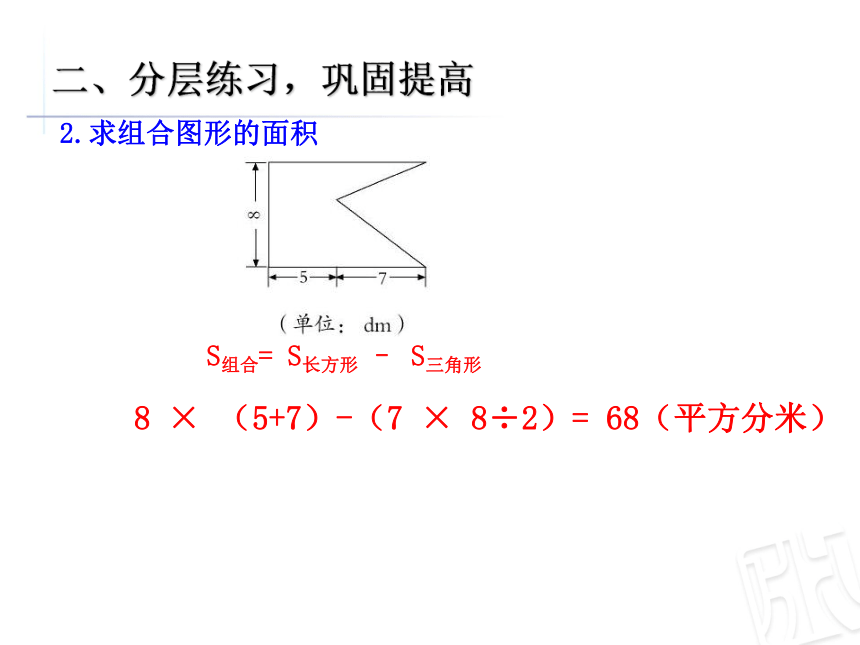
S组合= S长方形 – S三角形
8 × (5+7)-(7 × 8÷2)= 68(平方分米)
2.求组合图形的面积
2×26×10=520(平方厘米)
二、分层练习,巩固提高
3.求组合图形的面积
三、自主练习
4m
3m
7m
6m
6×4 +(7-4)×3
4.王老师要给自家客厅铺上地砖。下面是客厅平面图,铺地面积是多少平方米?
S组合图形=S长方形+S正方形
= 24 + 3×3
= 24 + 9
= 33(m2)
4m
3m
7m
6m
6×7 -(7-4)×(6-3)
S组合图形=S长方形-S正方形
= 42 - 3×3
= 42 - 9
= 33(m2)
答:铺地面积是33平方米。
答:铺地面积是33平方米。
分割
添补
比较
添补法
分割法
5.有一块五边形的沙发巾(如右图),制作这样一个沙发
巾需要多少平方厘米的布料?
三、自主练习
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料?
二、分层练习,巩固提高
S组合= S长方形 – S三角形
长方形面积:30×60=1800(平方厘米)
组合图形面积:1800-225= 1575(平方厘米)
两个三角形面积:(30÷2)×(60-45)÷2×2 =225(平方厘米)
12面锦旗面积:1575×12=18900(平方厘米)
6.学校举办歌咏比赛,要制作一些锦旗(样式如下图)。做12面锦旗需要多少平方厘米布?
7.草坪占地多少平方米?
三、自主练习
S组合图形 = S梯形 – S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
8.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平
方米需要用0.5千克涂料。如果涂料的价钱是每千克10
元,粉刷这面墙需要多少钱?
三、自主练习
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
四、回顾反思
《组合图形的面积练习》第8课时 课件
学习目标
通过引导回顾整理,加深对组合图形的特征和面积计算方法的理解,进一步理解并掌握求组合图形的面积就是求几个简单平面图形的面积的和或差的计算。
自学指导
认真看课本77、78页信息窗4内容思考:
1.怎样求多边形的面积?
2.求组合图形面积的一般方法有几种?
3分钟后看谁汇报地最好
求组合图形面积的一般方法:
⑴分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
⑵添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
一、问题回顾,再现新知
新图形
学过的图形
割、补、拼
转 化
想一想,怎样求多边形的面积?
一、问题回顾,再现新知
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
1.基本练习,巩固新知 求组合图形的面积。
二、分层练习,巩固提高
10cm
8cm
11cm
4cm
S组合= S大长方形 + S小长方形
10×8+(10-4)×(11-8)= 98(平方米)
10cm
8cm
11cm
4cm
S组合= S大长方形 - S小长方形
10×11-(11-8)×4 = 98(平方米)
二、分层练习,巩固提高
S组合= S长方形 – S三角形
8 × (5+7)-(7 × 8÷2)= 68(平方分米)
2.求组合图形的面积
2×26×10=520(平方厘米)
二、分层练习,巩固提高
3.求组合图形的面积
三、自主练习
4m
3m
7m
6m
6×4 +(7-4)×3
4.王老师要给自家客厅铺上地砖。下面是客厅平面图,铺地面积是多少平方米?
S组合图形=S长方形+S正方形
= 24 + 3×3
= 24 + 9
= 33(m2)
4m
3m
7m
6m
6×7 -(7-4)×(6-3)
S组合图形=S长方形-S正方形
= 42 - 3×3
= 42 - 9
= 33(m2)
答:铺地面积是33平方米。
答:铺地面积是33平方米。
分割
添补
比较
添补法
分割法
5.有一块五边形的沙发巾(如右图),制作这样一个沙发
巾需要多少平方厘米的布料?
三、自主练习
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料?
二、分层练习,巩固提高
S组合= S长方形 – S三角形
长方形面积:30×60=1800(平方厘米)
组合图形面积:1800-225= 1575(平方厘米)
两个三角形面积:(30÷2)×(60-45)÷2×2 =225(平方厘米)
12面锦旗面积:1575×12=18900(平方厘米)
6.学校举办歌咏比赛,要制作一些锦旗(样式如下图)。做12面锦旗需要多少平方厘米布?
7.草坪占地多少平方米?
三、自主练习
S组合图形 = S梯形 – S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
8.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平
方米需要用0.5千克涂料。如果涂料的价钱是每千克10
元,粉刷这面墙需要多少钱?
三、自主练习
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
四、回顾反思
