第二章 圆周运动 单元达标测试(word解析版)
文档属性
| 名称 | 第二章 圆周运动 单元达标测试(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 988.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-10 05:45:22 | ||
图片预览




文档简介
2021-2022学年粤教版(2019)必修第二册
第二章圆周运动 单元达标测试(解析版)
第I卷(选择题)
一、选择题(共60分)
1.如图所示,、是两个摩擦传动的靠背轮,是主动轮,是从动轮,它们的半径关系,和是轮边缘上的两个点,点是轮半径的中点,下列判断正确的是( )
A. B. C. D.
2.关于向心加速度的说法中正确的是( )
A.向心加速度的方向始终指向圆心
B.向心加速度同时改变线速度的大小与方向
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
3.火车转弯时,如果铁路弯道水平,外轨轮缘(图)的弹力提供了火车转弯的向心力(图),使得铁轨和轮缘极易受损。在实际修筑铁路时,弯道外的外轨会略高于内轨(图),当火车以规定的行驶速率转弯时,内外轨均不会受到轮缘的挤压,则下列说法正确的是( )
A.当火车的速率小于时,火车将有向外侧冲出轨道的危险
B.当火车的速率大于时,火车将挤压外轨道
C.当火车的速率小于时,内、外轨均不受到轮缘的挤压
D.当火车的质量改变时,规定的行驶速率将随之改变
4.如图所示,水平轨道与竖直光滑圆弧轨道相切于P点,一小球沿水平轨道向右运动,经过圆弧轨道的Q点时小球受到的作用力有(忽略空气阻力)( )
A.重力、弹力
B.重力、向心力
C.弹力、向心力
D.重力、弹力、向心力
5.如图所示的圆锥摆中,摆球A、B在同一水平面上做匀速圆周运动,关于A、B球的运动情况和受力情况,下列说法中正确的是( )
A.摆球A受重力、拉力和向心力的作用
B.摆球A所受的拉力小于摆球B所受的拉力
C.摆球A的速度小于摆球B的速度
D.A、B做匀速圆周运动的周期相等
6.一质量为2.0 × 103kg的汽车在水平公路上行驶,路面对轮胎的径向最大静摩擦力为1.4 × 104N,当汽车经过半径为100m的弯道时,下列判断正确的是( )
A.汽车转弯时所受的力有重力、弹力、摩擦力和向心力
B.汽车以某一速度转弯时,可不受径向摩擦力
C.汽车转弯的速度为30m/s时汽车会发生侧滑
D.汽车能安全转弯的向心加速度不超过8.0m/s2
7.如图,与水平面成角的倾斜匀质圆盘绕垂直于盘面的中心固定轴转动,一根不可伸长的细绳穿过圆盘中心,圆盘上方部分细绳与圆盘表面平行且与圆盘间无作用力,一端悬挂质量为的物块,另一端与随圆盘一起转动的物块相连,已知物块的质量为。物块与盘心的距离,与盘面之间的动摩擦因数,设最大静摩擦力等于滑动摩擦力,不考虑细绳与圆盘之间的摩擦力,g取,,。当物块始终保持静止时,圆盘转动的角速度可能为( )
A. B. C. D.
8.下列哪个物理量为标量( )
A.线速度 B.角速度 C.周期 D.向心力
9.未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示。当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力。为达到上述目的,下列说法正确的是( )
A.旋转舱的半径越大,转动的角速度就应越大
B.旋转舱的半径越大,转动的角速度就应越小
C.宇航员质量越大,旋转舱的角速度就应越大
D.宇航员质量的大小不影响旋转舱的角速度
10.如图所示,一个匀速转动的半径为r的水平圆盘上放着木块M和N,木块M放在圆盘的边缘处,木块N放在离圆心r的地方,它们都随圆盘一起运动。比较两木块的线速度、角速度和向心加速度的大小,下列说法正确的是( )
A.两木块的线速度相等
B.两木块的角速度相等
C.M的向心加速度是N的向心加速度的2倍
D.M的向心加速度是N的向心加速度的4倍
11.城市中为了解决交通问题,修建了许多立交桥。如图所示,桥面是半径为R的圆弧形的立交桥AB横跨在水平路面上,跨度为L,桥高为h。一辆质量为m的小汽车,在A端以速度v0冲上该立交桥,小汽车到达桥顶时的速度大小为v1,若小汽车在上桥过程中,始终未脱离桥面,则( )
A.小汽车通过桥顶时处于失重状态
B.小汽车上到桥顶时受到桥面的支持力大小为
C.小汽车到达桥顶时的速度有可能大于
D.小汽车到达桥顶时对桥面的压力有可能为零
12.游乐场中的摩天轮,其运动可视为匀速圆周运动。关于匀速圆周运动的物体,下列说法错误的是( )
A.物体的匀速圆周运动是变速运动
B.物体在任意相等时间内通过的位移相等
C.物体所受的合力始终指向圆心
D.物体所受的合力只改变速度的大小,不改变速度的方向
第II卷(非选择题)
二、解答题(共40分)
13.兴趣小组为了测量吊扇的角速度,设计了如下实验:把吊扇的扇叶拆除,将质量为m的小球,用长为L的轻绳悬挂在半径为R的机头边缘。给机头通电,待稳定后,小球随机头一起在水平面内做匀速圆周机头运动。轻绳与竖直方向的夹角为θ,重力加速度为g,忽略空气阻力,求:
(1)小球做圆周运动的半径r;
(2)小球做圆周运动的向心力大小;
(3)机头匀速转动的角速度。
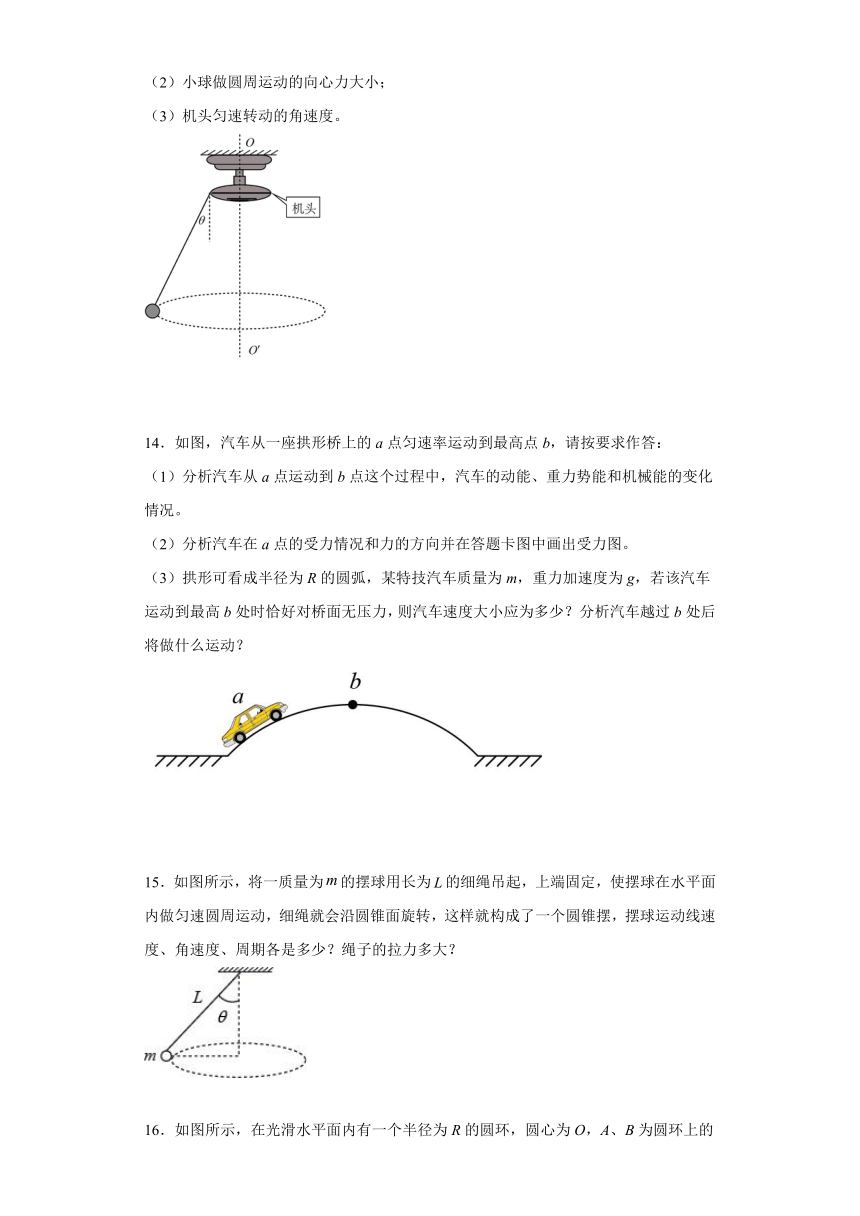
14.如图,汽车从一座拱形桥上的a点匀速率运动到最高点b,请按要求作答:
(1)分析汽车从a点运动到b点这个过程中,汽车的动能、重力势能和机械能的变化情况。
(2)分析汽车在a点的受力情况和力的方向并在答题卡图中画出受力图。
(3)拱形可看成半径为R的圆弧,某特技汽车质量为m,重力加速度为g,若该汽车运动到最高b处时恰好对桥面无压力,则汽车速度大小应为多少?分析汽车越过b处后将做什么运动?
15.如图所示,将一质量为的摆球用长为的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,摆球运动线速度、角速度、周期各是多少?绳子的拉力多大?
16.如图所示,在光滑水平面内有一个半径为R的圆环,圆心为O,A、B为圆环上的两个小孔,AB连线为圆的直径,C为水平面上一点,OC与AB夹角=60°。圆环绕圆心沿顺时针方向做匀速圆周运动。一个质量为m的小球在位于C处的质点吸引力作用,绕C点做匀速圆周运动,引力大小恒为小球重力的倍。图示时刻小球通过小孔A沿半径方向进入圆环内,恰好通过B孔到达圆环外部。已知重力加速度为g。求:
(1)小球运动的线速度大小;
(2)圆环转动的角速度大小。
参考答案
1.B
【详解】
AD.因AB两轮边缘的线速度相同,则根据
可知,角速度
根据
可知
即AD错误;
CD.因ac两点同轴转动,则角速度相等,即
则
根据
可知
选项B正确,C错误。
故选B。
2.A
【详解】
A.向心加速度的方向始终指向圆心,绕着圆心转动,其方向时刻在改变,故A正确;
B.向心加速度方向与线速度方向垂直,只改变线速度的方向,不改变线速度的大小,故B错误;
CD.匀速圆周运动的向心加速度大小不变,方向时刻在变化。所以,匀速圆周运动的向心加速度在不断变化,故CD错误。
故选A。
3.B
【详解】
AC.当火车以规定的行驶速率转弯时,内外轨均不会受到轮缘的挤压,火车靠重力和支持力的合力提供向心力,当火车速率小于时,重力和支持力的合力大于向心力,火车会挤压内轨,故AC错误;
B.当火车的速率大于,重力和支持力的合力不够提供向心力,有离心的趋势,会挤压外轨,故B正确;
D.当火车以规定的行驶速率行驶时,由重力和支持力的合力提供向心力
可得规定速率
与火车质量无关,故D错误。
故选B。
4.A
【详解】
小球受到的作用力有重力、弹力,二力沿圆心方向的合力提供向心力。
故选A。
5.D
【详解】
A.向心力是效果力,在受力分析时不能说物体受到了向心力,摆球A受重力、绳拉力的作用,它们的合力提供摆球做匀速圆周运动所需向心力,故A错误;
B.摆球在同一水平面上做匀速圆周运动,设绳与竖直方向夹角为,可得绳的拉力大小
满足
由于不知道摆球A、B的质量大小关系,故摆球A所受的拉力与摆球B所受的拉力大小关系不能确定,故B错误;
CD.根据牛顿第二定律可知
可知摆球A、B做匀速圆周运动的周期相等,根据
由于
所以
故C错误,D正确。
故选D。
6.C
【详解】
A.分析受力只能分析性质力,不能添加效果力,所以汽车转弯时所受的力有重力、弹力、摩擦力,A错误;
B.汽车在水平路面转弯,摩擦力提供向心力,B错误;
C.由
N = 1.8 × 104N
即汽车转弯的速度为30m/s时,所需向心力1.8 × 104N,大于路面可提供的最大静摩擦力1.4 × 104N,汽车会发生侧滑,C正确;
D.由,解得a = 7.0m/s2,即汽车能安全转弯的向心加速度不超过7.0m/s2,D错误。
故选C。
7.C
【详解】
物块B随圆盘转动过程中物块A始终保持静止,说明细绳内的拉力
假设物块B转到最高点时,设圆盘转动的最大角速度为,对物块B有
设圆盘转动的最小角速度为,对物块B有
物块B转到最低点时,因
所以物块B转到最低点时的最小角速度为0,设圆盘转动的最大角速度为,对物块B有
综上分析可知,圆盘转动的角速度为
代入数据解得
故C正确,ABD错误。
故选C。
8.BC
【详解】
BC.只有大小,没有方向的物理量是标量,如路程、角速度、质量、周期等都是标量,B、C均为标量,BC正确;
AD.既有大小又有方向,相加时遵循平行四边形定则的物理量是矢量,如线速度、力、速度、加速度、位移、动量等都是矢量,AD错误。
故选BC。
9.BD
【详解】
AB.由题意可得
联立可得
故旋转舱的半径越大,转动的角速度就应越小,A错误,B正确;
CD.宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力,即向心加速度为g即可,与宇航员的质量无关,C错误,D正确。
故选BD。
10.BC
【详解】
由圆周运动知识得,M、N两木块有相同的角速度;由v=ωr及rN=r、rM=r知,木块M的线速度是木块N的线速度的2倍;由
a=ω2r
得M的向心加速度是N的向心加速度的2倍。
故选BC。
11.AD
【详解】
A.小汽车做圆周运动,在最高点合力提供向心力,方向指向圆心,所以加速度方向竖直向下,汽车处于失重状态,故A正确;
B.在最高点,根据向心力公式得
解得
但在其它位置,受到桥面的支持力大小不为
故B错误;
CD.在最高点,根据向心力公式得
当N=0时,速度最大
故C错误,D正确。
故选AD。
12.BD
【详解】
A.物体的匀速圆周运动是速度大小不变,方向不断改变的变速运动,故A正确,不符合题意;
B.做匀速圆周运动的物体任意相等时间内通过的位移大小相等,方向不同,故B错误,符合题意;
C.做匀速圆周运动的物体所受的合力始终指向圆心,故C正确,不符合题意;
D.做匀速圆周运动的物体所受的合力只改变速度的方向,不改变速度的大小,故D错误,符合题意。
故选BD。
13.(1);(2);(3)
【详解】
(1)小球做圆周运动的半径
(2)小球做圆周运动的向心力大小
(3)由牛顿第二定律得:
14.(1)动能保持不变,重力势能一直增大,机械能一直增大;(2)见解析;(3),过b后将做平抛运动。
【详解】
(1)由于匀速率运动,在上升的过程中,汽车的动能保持不变,重力势能一直增大,机械能一直增大。
(2)汽车受牵引力、重力、支持力和阻力作用,受力情况分析如图
(3)在b处对桥面无压力,重力充当向心力,因此有
可得
汽车过b后由于只受重力,竖直方向初速度为零,因此做平抛运动。
15.,,,
【详解】
摆球受力分析,如图所示
摆球的合力提供向心力,由牛顿第二定律得
由几何关系,可得摆球轨迹半径为
联立解得
绳子的拉力为
16.(1);(2)(n=0,1,2……)
【详解】
(1)连线AC,则AC为小球做圆周运动的半径r,根据速度沿轨迹切线,可知β=30°,
则
小球由吸引力提供向心力可知
解得
(2)小球转过的圆心角为
小球在圆环内运动时间为
小球从B孔穿出的过程,圆环上的小孔B转过的角度为
,(n=0,1,2……)
圆环的转动时间
根据等时性可知
t1=t2
解得
(n=0,1,2……)
第二章圆周运动 单元达标测试(解析版)
第I卷(选择题)
一、选择题(共60分)
1.如图所示,、是两个摩擦传动的靠背轮,是主动轮,是从动轮,它们的半径关系,和是轮边缘上的两个点,点是轮半径的中点,下列判断正确的是( )
A. B. C. D.
2.关于向心加速度的说法中正确的是( )
A.向心加速度的方向始终指向圆心
B.向心加速度同时改变线速度的大小与方向
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
3.火车转弯时,如果铁路弯道水平,外轨轮缘(图)的弹力提供了火车转弯的向心力(图),使得铁轨和轮缘极易受损。在实际修筑铁路时,弯道外的外轨会略高于内轨(图),当火车以规定的行驶速率转弯时,内外轨均不会受到轮缘的挤压,则下列说法正确的是( )
A.当火车的速率小于时,火车将有向外侧冲出轨道的危险
B.当火车的速率大于时,火车将挤压外轨道
C.当火车的速率小于时,内、外轨均不受到轮缘的挤压
D.当火车的质量改变时,规定的行驶速率将随之改变
4.如图所示,水平轨道与竖直光滑圆弧轨道相切于P点,一小球沿水平轨道向右运动,经过圆弧轨道的Q点时小球受到的作用力有(忽略空气阻力)( )
A.重力、弹力
B.重力、向心力
C.弹力、向心力
D.重力、弹力、向心力
5.如图所示的圆锥摆中,摆球A、B在同一水平面上做匀速圆周运动,关于A、B球的运动情况和受力情况,下列说法中正确的是( )
A.摆球A受重力、拉力和向心力的作用
B.摆球A所受的拉力小于摆球B所受的拉力
C.摆球A的速度小于摆球B的速度
D.A、B做匀速圆周运动的周期相等
6.一质量为2.0 × 103kg的汽车在水平公路上行驶,路面对轮胎的径向最大静摩擦力为1.4 × 104N,当汽车经过半径为100m的弯道时,下列判断正确的是( )
A.汽车转弯时所受的力有重力、弹力、摩擦力和向心力
B.汽车以某一速度转弯时,可不受径向摩擦力
C.汽车转弯的速度为30m/s时汽车会发生侧滑
D.汽车能安全转弯的向心加速度不超过8.0m/s2
7.如图,与水平面成角的倾斜匀质圆盘绕垂直于盘面的中心固定轴转动,一根不可伸长的细绳穿过圆盘中心,圆盘上方部分细绳与圆盘表面平行且与圆盘间无作用力,一端悬挂质量为的物块,另一端与随圆盘一起转动的物块相连,已知物块的质量为。物块与盘心的距离,与盘面之间的动摩擦因数,设最大静摩擦力等于滑动摩擦力,不考虑细绳与圆盘之间的摩擦力,g取,,。当物块始终保持静止时,圆盘转动的角速度可能为( )
A. B. C. D.
8.下列哪个物理量为标量( )
A.线速度 B.角速度 C.周期 D.向心力
9.未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示。当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力。为达到上述目的,下列说法正确的是( )
A.旋转舱的半径越大,转动的角速度就应越大
B.旋转舱的半径越大,转动的角速度就应越小
C.宇航员质量越大,旋转舱的角速度就应越大
D.宇航员质量的大小不影响旋转舱的角速度
10.如图所示,一个匀速转动的半径为r的水平圆盘上放着木块M和N,木块M放在圆盘的边缘处,木块N放在离圆心r的地方,它们都随圆盘一起运动。比较两木块的线速度、角速度和向心加速度的大小,下列说法正确的是( )
A.两木块的线速度相等
B.两木块的角速度相等
C.M的向心加速度是N的向心加速度的2倍
D.M的向心加速度是N的向心加速度的4倍
11.城市中为了解决交通问题,修建了许多立交桥。如图所示,桥面是半径为R的圆弧形的立交桥AB横跨在水平路面上,跨度为L,桥高为h。一辆质量为m的小汽车,在A端以速度v0冲上该立交桥,小汽车到达桥顶时的速度大小为v1,若小汽车在上桥过程中,始终未脱离桥面,则( )
A.小汽车通过桥顶时处于失重状态
B.小汽车上到桥顶时受到桥面的支持力大小为
C.小汽车到达桥顶时的速度有可能大于
D.小汽车到达桥顶时对桥面的压力有可能为零
12.游乐场中的摩天轮,其运动可视为匀速圆周运动。关于匀速圆周运动的物体,下列说法错误的是( )
A.物体的匀速圆周运动是变速运动
B.物体在任意相等时间内通过的位移相等
C.物体所受的合力始终指向圆心
D.物体所受的合力只改变速度的大小,不改变速度的方向
第II卷(非选择题)
二、解答题(共40分)
13.兴趣小组为了测量吊扇的角速度,设计了如下实验:把吊扇的扇叶拆除,将质量为m的小球,用长为L的轻绳悬挂在半径为R的机头边缘。给机头通电,待稳定后,小球随机头一起在水平面内做匀速圆周机头运动。轻绳与竖直方向的夹角为θ,重力加速度为g,忽略空气阻力,求:
(1)小球做圆周运动的半径r;
(2)小球做圆周运动的向心力大小;
(3)机头匀速转动的角速度。
14.如图,汽车从一座拱形桥上的a点匀速率运动到最高点b,请按要求作答:
(1)分析汽车从a点运动到b点这个过程中,汽车的动能、重力势能和机械能的变化情况。
(2)分析汽车在a点的受力情况和力的方向并在答题卡图中画出受力图。
(3)拱形可看成半径为R的圆弧,某特技汽车质量为m,重力加速度为g,若该汽车运动到最高b处时恰好对桥面无压力,则汽车速度大小应为多少?分析汽车越过b处后将做什么运动?
15.如图所示,将一质量为的摆球用长为的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆,摆球运动线速度、角速度、周期各是多少?绳子的拉力多大?
16.如图所示,在光滑水平面内有一个半径为R的圆环,圆心为O,A、B为圆环上的两个小孔,AB连线为圆的直径,C为水平面上一点,OC与AB夹角=60°。圆环绕圆心沿顺时针方向做匀速圆周运动。一个质量为m的小球在位于C处的质点吸引力作用,绕C点做匀速圆周运动,引力大小恒为小球重力的倍。图示时刻小球通过小孔A沿半径方向进入圆环内,恰好通过B孔到达圆环外部。已知重力加速度为g。求:
(1)小球运动的线速度大小;
(2)圆环转动的角速度大小。
参考答案
1.B
【详解】
AD.因AB两轮边缘的线速度相同,则根据
可知,角速度
根据
可知
即AD错误;
CD.因ac两点同轴转动,则角速度相等,即
则
根据
可知
选项B正确,C错误。
故选B。
2.A
【详解】
A.向心加速度的方向始终指向圆心,绕着圆心转动,其方向时刻在改变,故A正确;
B.向心加速度方向与线速度方向垂直,只改变线速度的方向,不改变线速度的大小,故B错误;
CD.匀速圆周运动的向心加速度大小不变,方向时刻在变化。所以,匀速圆周运动的向心加速度在不断变化,故CD错误。
故选A。
3.B
【详解】
AC.当火车以规定的行驶速率转弯时,内外轨均不会受到轮缘的挤压,火车靠重力和支持力的合力提供向心力,当火车速率小于时,重力和支持力的合力大于向心力,火车会挤压内轨,故AC错误;
B.当火车的速率大于,重力和支持力的合力不够提供向心力,有离心的趋势,会挤压外轨,故B正确;
D.当火车以规定的行驶速率行驶时,由重力和支持力的合力提供向心力
可得规定速率
与火车质量无关,故D错误。
故选B。
4.A
【详解】
小球受到的作用力有重力、弹力,二力沿圆心方向的合力提供向心力。
故选A。
5.D
【详解】
A.向心力是效果力,在受力分析时不能说物体受到了向心力,摆球A受重力、绳拉力的作用,它们的合力提供摆球做匀速圆周运动所需向心力,故A错误;
B.摆球在同一水平面上做匀速圆周运动,设绳与竖直方向夹角为,可得绳的拉力大小
满足
由于不知道摆球A、B的质量大小关系,故摆球A所受的拉力与摆球B所受的拉力大小关系不能确定,故B错误;
CD.根据牛顿第二定律可知
可知摆球A、B做匀速圆周运动的周期相等,根据
由于
所以
故C错误,D正确。
故选D。
6.C
【详解】
A.分析受力只能分析性质力,不能添加效果力,所以汽车转弯时所受的力有重力、弹力、摩擦力,A错误;
B.汽车在水平路面转弯,摩擦力提供向心力,B错误;
C.由
N = 1.8 × 104N
即汽车转弯的速度为30m/s时,所需向心力1.8 × 104N,大于路面可提供的最大静摩擦力1.4 × 104N,汽车会发生侧滑,C正确;
D.由,解得a = 7.0m/s2,即汽车能安全转弯的向心加速度不超过7.0m/s2,D错误。
故选C。
7.C
【详解】
物块B随圆盘转动过程中物块A始终保持静止,说明细绳内的拉力
假设物块B转到最高点时,设圆盘转动的最大角速度为,对物块B有
设圆盘转动的最小角速度为,对物块B有
物块B转到最低点时,因
所以物块B转到最低点时的最小角速度为0,设圆盘转动的最大角速度为,对物块B有
综上分析可知,圆盘转动的角速度为
代入数据解得
故C正确,ABD错误。
故选C。
8.BC
【详解】
BC.只有大小,没有方向的物理量是标量,如路程、角速度、质量、周期等都是标量,B、C均为标量,BC正确;
AD.既有大小又有方向,相加时遵循平行四边形定则的物理量是矢量,如线速度、力、速度、加速度、位移、动量等都是矢量,AD错误。
故选BC。
9.BD
【详解】
AB.由题意可得
联立可得
故旋转舱的半径越大,转动的角速度就应越小,A错误,B正确;
CD.宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力,即向心加速度为g即可,与宇航员的质量无关,C错误,D正确。
故选BD。
10.BC
【详解】
由圆周运动知识得,M、N两木块有相同的角速度;由v=ωr及rN=r、rM=r知,木块M的线速度是木块N的线速度的2倍;由
a=ω2r
得M的向心加速度是N的向心加速度的2倍。
故选BC。
11.AD
【详解】
A.小汽车做圆周运动,在最高点合力提供向心力,方向指向圆心,所以加速度方向竖直向下,汽车处于失重状态,故A正确;
B.在最高点,根据向心力公式得
解得
但在其它位置,受到桥面的支持力大小不为
故B错误;
CD.在最高点,根据向心力公式得
当N=0时,速度最大
故C错误,D正确。
故选AD。
12.BD
【详解】
A.物体的匀速圆周运动是速度大小不变,方向不断改变的变速运动,故A正确,不符合题意;
B.做匀速圆周运动的物体任意相等时间内通过的位移大小相等,方向不同,故B错误,符合题意;
C.做匀速圆周运动的物体所受的合力始终指向圆心,故C正确,不符合题意;
D.做匀速圆周运动的物体所受的合力只改变速度的方向,不改变速度的大小,故D错误,符合题意。
故选BD。
13.(1);(2);(3)
【详解】
(1)小球做圆周运动的半径
(2)小球做圆周运动的向心力大小
(3)由牛顿第二定律得:
14.(1)动能保持不变,重力势能一直增大,机械能一直增大;(2)见解析;(3),过b后将做平抛运动。
【详解】
(1)由于匀速率运动,在上升的过程中,汽车的动能保持不变,重力势能一直增大,机械能一直增大。
(2)汽车受牵引力、重力、支持力和阻力作用,受力情况分析如图
(3)在b处对桥面无压力,重力充当向心力,因此有
可得
汽车过b后由于只受重力,竖直方向初速度为零,因此做平抛运动。
15.,,,
【详解】
摆球受力分析,如图所示
摆球的合力提供向心力,由牛顿第二定律得
由几何关系,可得摆球轨迹半径为
联立解得
绳子的拉力为
16.(1);(2)(n=0,1,2……)
【详解】
(1)连线AC,则AC为小球做圆周运动的半径r,根据速度沿轨迹切线,可知β=30°,
则
小球由吸引力提供向心力可知
解得
(2)小球转过的圆心角为
小球在圆环内运动时间为
小球从B孔穿出的过程,圆环上的小孔B转过的角度为
,(n=0,1,2……)
圆环的转动时间
根据等时性可知
t1=t2
解得
(n=0,1,2……)
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
