苏科版八年级数学上册 2.2 轴对称的性质(共27张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 2.2 轴对称的性质(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 736.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 18:51:01 | ||
图片预览




文档简介
(共27张PPT)
轴对称的性质
轴对称
轴对称图形
一个图形沿着某一条直线折叠,如果它能够与另一个图形______,那么就说这两个图形成轴对称.这条直线就是______.两个图形中的对应点叫做对称点.
一个图形沿着某条直线对折,如果直线两旁的部分能够完全_____,那么就称这个图形是轴对称图形.
轴对称与轴对称图形之间有什么区别
复习:
请找出下列符号所蕴含的内在规律,然后在横线上设计一个恰当的图形.
(哈佛大学77年入学考试试题)
一、轴对称的性质
实验一:将一张纸对折,用笔通一个洞,记两个洞为A、A1,折痕为m,想一想:
(1)点A与点A1关于直线m有什么样的位置关系
(2)连结AA1,请同学们用量角器、刻度尺度量并判断线段AA1与直线m有什么关系?
A
A1
m
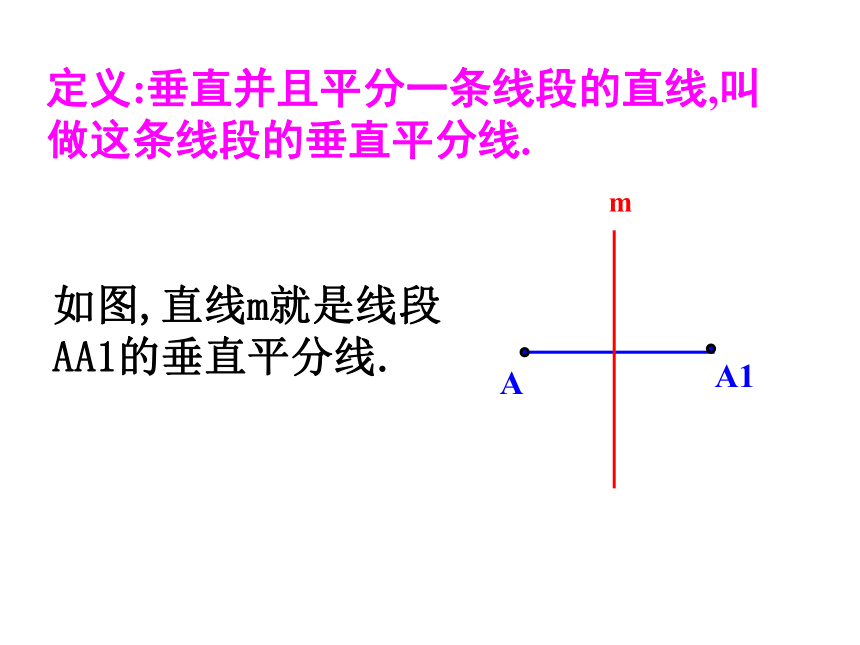
定义:垂直并且平分一条线段的直线,叫做这条线段的垂直平分线.
A
A1
m
如图,直线m就是线段AA1的垂直平分线.
C1
A
B
C
A1
B1
m
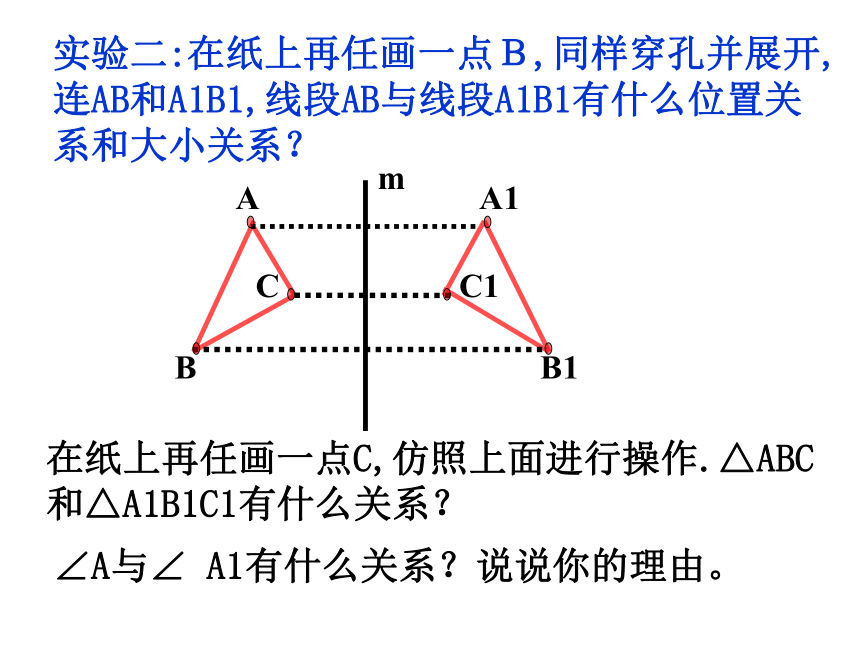
实验二:在纸上再任画一点B,同样穿孔并展开,连AB和A1B1,线段AB与线段A1B1有什么位置关系和大小关系?
在纸上再任画一点C,仿照上面进行操作.△ABC和△A1B1C1有什么关系?
∠A与∠ A1有什么关系?说说你的理由。
C1
A
B
C
A1
B1
m
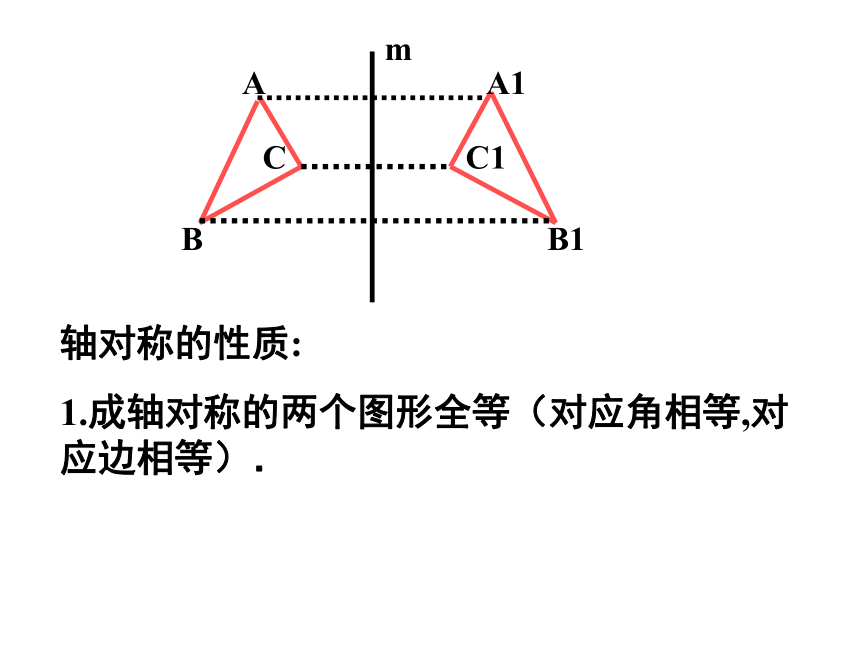
轴对称的性质:
1.成轴对称的两个图形全等(对应角相等,对应边相等).
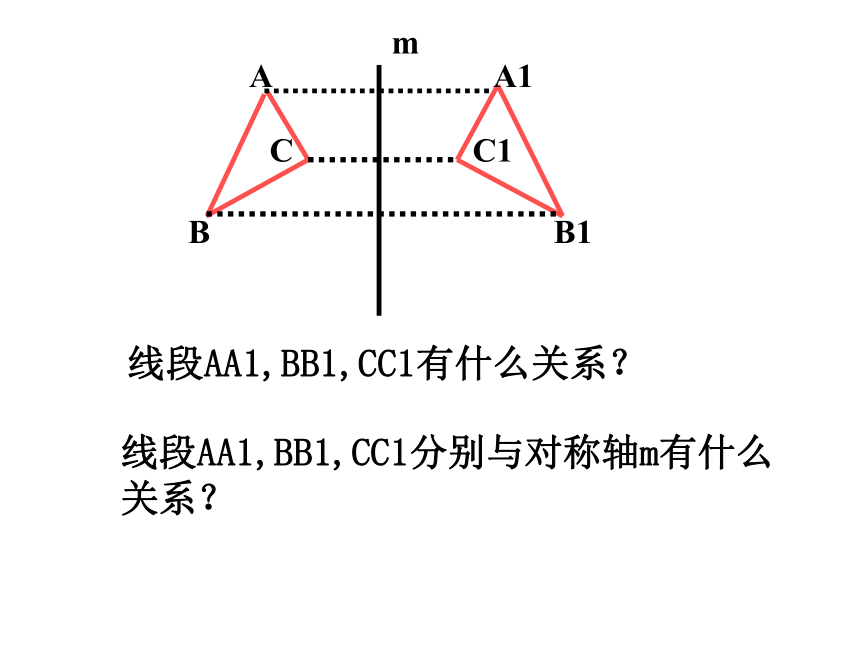
线段AA1,BB1,CC1有什么关系?
C1
A
B
C
A1
B1
m
线段AA1,BB1,CC1分别与对称轴m有什么关系?
m
C1
A
B
C
A1
B1
轴对称的性质:
2.成轴对称的两个图形,对称点所连的线段平行(或在同一条直线上).
3.成轴对称的两个图形,对称点所连的线段被对称轴垂直平分.
如果两个图形成轴对称,那么对称轴是对称点所连的线段的垂直平分线.
C1
A
B
C
A1
B1
m
小结:轴对称的性质:
1.成轴对称的两个图
形全等(对应角相
等,对应边相等).
2.成轴对称的两个图形,对称点所连的线段平行(或在同一条直线上).
3.成轴对称的两个图形,对称点所连的线段被对称轴垂直平分.
如果两个图形成轴对称,那么对称轴是对称点所连的线段的垂直平分线.
基础训练
1.若线段AB和A′B′关于直线l对称,
则AB=A′B′ ( )
2.若线段AB和A′B′在直线l的两旁,且AB=A′B′,则线段AB和A′B′关于直线l对称( )
3.若点A与A′到直线l的距离相等,则若点A与A′关于直线l对称 ( )
4.若△ABC≌△A′B′C′,则△ABC和△A′B′C′,关于某直线对称 ( )
√
×
×
×
(一)判断
二、轴对称作图题
例1、如图,两个三角形成轴对称,不用折叠的方法你能画出对称轴吗?与同伴交流你的做法.
∟
m
方法:连接对称点,并作这条线段的垂直平分线,即为所求的对称轴.
(二)如果直线l外有一点A,那么怎样画出点A关于直线l的对称点A′
●
●
A
A′
l
O
┏
如果直线l外有线段AB,那么怎样画出线段AB关于直线l 的对称线段A′B′
●
A
l
B
●
变:如果直线l外有线段AB,那么怎样画出线段AB关于直线l的对称线段A′B′
●
●
A
A′
l
O
B
●
●
B′
l
l
A
B
A
B
A′
B′
A′
B′
1.如图,画出△ABC关于直线MN的对称图形.
A
A′
C
B
B′
C′
N
M
●
●
●
N
M
A
C
B
F
E
D
H
P
G
Q
如右图,四边形ABCD与四边形EFGH关于直线MN的对称,ACBD交于P,怎样找出点P关于直线MN的对称点Q
成轴对称的两个图形的任何对应部分也成轴对称
拓展与操作
2.下图是由半圆和三角形组成的图形,请以AB为对称轴,作出图形的另一半(用尺规作图,保留作图痕迹)
●
A
B
■把一圆形纸片对折后,得到右图,然后沿虚线剪开,得到两部分,
其中一部分展开后的平面
图形是( )
A
B
C
D
B
回顾与思考
通过本节课的学习,你有什么收获呢?
轴对称的性质拓展延伸
例1:平面镜中的对称问题
(1)下图是从镜中看到的一串数字,这串数字应为 .
(2)一辆牌照为18118的汽车停在水坑上,则牌照映在水中的数字为 .
(3) 小明在洗澡时从平面镜中看到墙壁上钟表的时间是3:30,你知道此时的实际时间是多少?
小技巧:左右相反,上下不变
A
B
A′
如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?
E
F
G
H
例2:台球与轴对称
解:1.作点A关于EF的对称点A′
2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。
C
例3:作图法求最短距离
■在正方形ABCD上,P在AC上,E是AB上一定点,则当点P运动到何处时,△PBE的周长最小
C
A
B
D
P
E
变:如图,已知,∠AOB内有一点P,求作△PQR,使Q在OA 上,R在OB上,且使△PQR的周长最小.
轴对称的性质
轴对称
轴对称图形
一个图形沿着某一条直线折叠,如果它能够与另一个图形______,那么就说这两个图形成轴对称.这条直线就是______.两个图形中的对应点叫做对称点.
一个图形沿着某条直线对折,如果直线两旁的部分能够完全_____,那么就称这个图形是轴对称图形.
轴对称与轴对称图形之间有什么区别
复习:
请找出下列符号所蕴含的内在规律,然后在横线上设计一个恰当的图形.
(哈佛大学77年入学考试试题)
一、轴对称的性质
实验一:将一张纸对折,用笔通一个洞,记两个洞为A、A1,折痕为m,想一想:
(1)点A与点A1关于直线m有什么样的位置关系
(2)连结AA1,请同学们用量角器、刻度尺度量并判断线段AA1与直线m有什么关系?
A
A1
m
定义:垂直并且平分一条线段的直线,叫做这条线段的垂直平分线.
A
A1
m
如图,直线m就是线段AA1的垂直平分线.
C1
A
B
C
A1
B1
m
实验二:在纸上再任画一点B,同样穿孔并展开,连AB和A1B1,线段AB与线段A1B1有什么位置关系和大小关系?
在纸上再任画一点C,仿照上面进行操作.△ABC和△A1B1C1有什么关系?
∠A与∠ A1有什么关系?说说你的理由。
C1
A
B
C
A1
B1
m
轴对称的性质:
1.成轴对称的两个图形全等(对应角相等,对应边相等).
线段AA1,BB1,CC1有什么关系?
C1
A
B
C
A1
B1
m
线段AA1,BB1,CC1分别与对称轴m有什么关系?
m
C1
A
B
C
A1
B1
轴对称的性质:
2.成轴对称的两个图形,对称点所连的线段平行(或在同一条直线上).
3.成轴对称的两个图形,对称点所连的线段被对称轴垂直平分.
如果两个图形成轴对称,那么对称轴是对称点所连的线段的垂直平分线.
C1
A
B
C
A1
B1
m
小结:轴对称的性质:
1.成轴对称的两个图
形全等(对应角相
等,对应边相等).
2.成轴对称的两个图形,对称点所连的线段平行(或在同一条直线上).
3.成轴对称的两个图形,对称点所连的线段被对称轴垂直平分.
如果两个图形成轴对称,那么对称轴是对称点所连的线段的垂直平分线.
基础训练
1.若线段AB和A′B′关于直线l对称,
则AB=A′B′ ( )
2.若线段AB和A′B′在直线l的两旁,且AB=A′B′,则线段AB和A′B′关于直线l对称( )
3.若点A与A′到直线l的距离相等,则若点A与A′关于直线l对称 ( )
4.若△ABC≌△A′B′C′,则△ABC和△A′B′C′,关于某直线对称 ( )
√
×
×
×
(一)判断
二、轴对称作图题
例1、如图,两个三角形成轴对称,不用折叠的方法你能画出对称轴吗?与同伴交流你的做法.
∟
m
方法:连接对称点,并作这条线段的垂直平分线,即为所求的对称轴.
(二)如果直线l外有一点A,那么怎样画出点A关于直线l的对称点A′
●
●
A
A′
l
O
┏
如果直线l外有线段AB,那么怎样画出线段AB关于直线l 的对称线段A′B′
●
A
l
B
●
变:如果直线l外有线段AB,那么怎样画出线段AB关于直线l的对称线段A′B′
●
●
A
A′
l
O
B
●
●
B′
l
l
A
B
A
B
A′
B′
A′
B′
1.如图,画出△ABC关于直线MN的对称图形.
A
A′
C
B
B′
C′
N
M
●
●
●
N
M
A
C
B
F
E
D
H
P
G
Q
如右图,四边形ABCD与四边形EFGH关于直线MN的对称,ACBD交于P,怎样找出点P关于直线MN的对称点Q
成轴对称的两个图形的任何对应部分也成轴对称
拓展与操作
2.下图是由半圆和三角形组成的图形,请以AB为对称轴,作出图形的另一半(用尺规作图,保留作图痕迹)
●
A
B
■把一圆形纸片对折后,得到右图,然后沿虚线剪开,得到两部分,
其中一部分展开后的平面
图形是( )
A
B
C
D
B
回顾与思考
通过本节课的学习,你有什么收获呢?
轴对称的性质拓展延伸
例1:平面镜中的对称问题
(1)下图是从镜中看到的一串数字,这串数字应为 .
(2)一辆牌照为18118的汽车停在水坑上,则牌照映在水中的数字为 .
(3) 小明在洗澡时从平面镜中看到墙壁上钟表的时间是3:30,你知道此时的实际时间是多少?
小技巧:左右相反,上下不变
A
B
A′
如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?
E
F
G
H
例2:台球与轴对称
解:1.作点A关于EF的对称点A′
2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。
C
例3:作图法求最短距离
■在正方形ABCD上,P在AC上,E是AB上一定点,则当点P运动到何处时,△PBE的周长最小
C
A
B
D
P
E
变:如图,已知,∠AOB内有一点P,求作△PQR,使Q在OA 上,R在OB上,且使△PQR的周长最小.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
