苏科版八年级数学上册 1.3 探索三角形全等的条件(共18张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 1.3 探索三角形全等的条件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 19:21:52 | ||
图片预览




文档简介
(共18张PPT)
八年级(上册)
初中数学
1.3 探索三角形全等的条件(1)
问题情境:
(1)如图,△ABC≌△DEF,你能得出哪些结论?
1.3 探索三角形全等的条件(1)
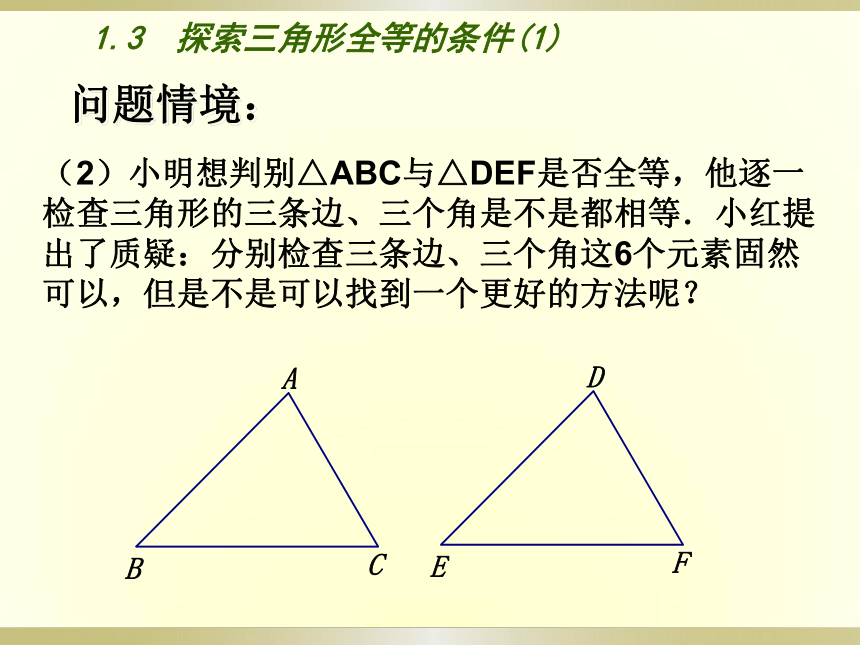
(2)小明想判别△ABC与△DEF是否全等,他逐一检查三角形的三条边、三个角是不是都相等.小红提出了质疑:分别检查三条边、三个角这6个元素固然可以,但是不是可以找到一个更好的方法呢?
问题情境:
1.3 探索三角形全等的条件(1)
讨论交流:
1.当两个三角形的1对边或角相等时,它们全等吗?
2.当两个三角形的2对边或角分别相等时,它们全
等吗?
3.当两个三角形的3对边或角分别相等时,它们全
等吗?
1.3 探索三角形全等的条件(1)
探索活动:
(一)如图,每人用一张长方形纸片剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?
1.3 探索三角形全等的条件(1)
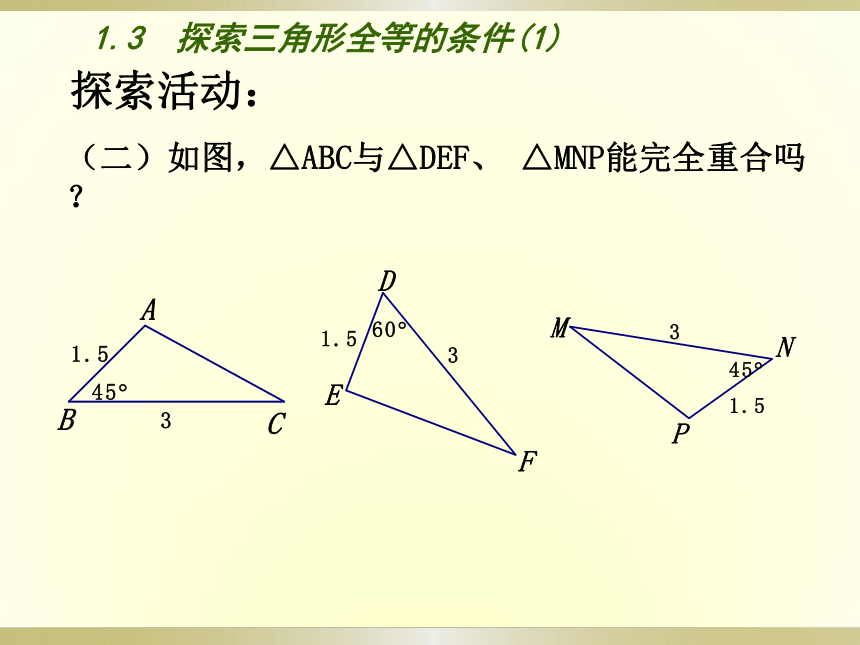
(二)如图,△ABC与△DEF、 △MNP能完全重合吗?
1.3 探索三角形全等的条件(1)
探索活动:
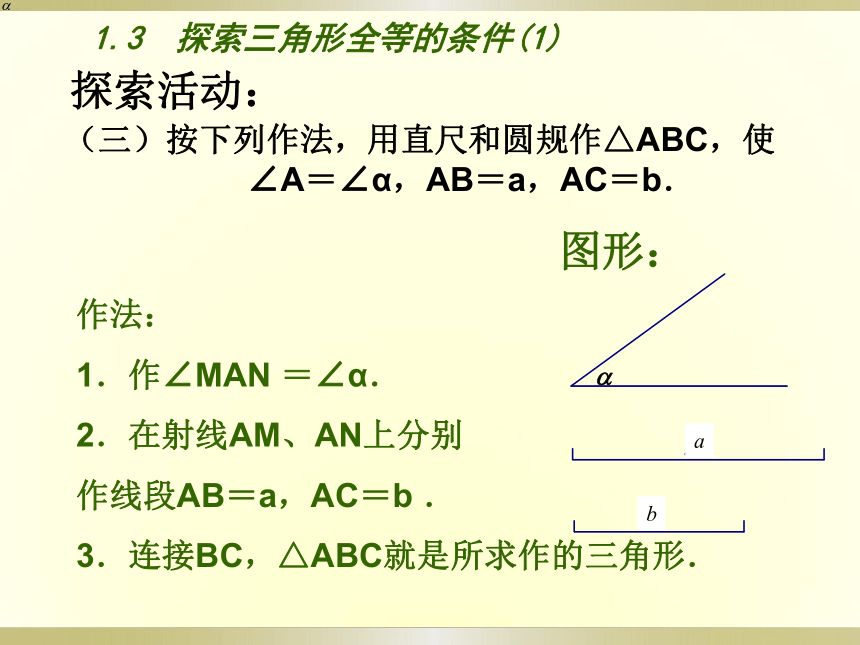
(三)按下列作法,用直尺和圆规作△ABC,使
∠A=∠α,AB=a,AC=b.
作法:
1.作∠MAN =∠α.
2.在射线AM、AN上分别
作线段AB=a,AC=b .
3.连接BC,△ABC就是所求作的三角形.
图形:
a
b
1.3 探索三角形全等的条件(1)
探索活动:
提炼归纳:
基本事实:
两边及其夹角分别相等的两个三角形全等(简写成
“边角边”或“SAS”) .
几何语言:
∵在△ABC和△DEF中,
AB=DE,
∠B=∠E,
BC=EF,
∴ △ABC ≌ △DEF(SAS).
1.3 探索三角形全等的条件(1)
新知应用:
例1 如图,AB =AD,∠BAC =∠DAC.
求证:△ABC ≌ △ADC.
证明:在△ABC和△ADC中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
1.3 探索三角形全等的条件(1)
如图,AB =AD,∠BAC =∠DAC.
变式拓展:
(1)DC =BC吗?
(2)CA平分∠DCB吗?
(3)本例包含哪一种图形变换?
1.3 探索三角形全等的条件(1)
练一练:
如图,AB=AC,AE=AF,
求证:△AFB≌△AEC.
例2 已知:如图,AB、CD相交于点E,且E是AB、CD的中点.
求证:①△AEC≌△BED.
②AC∥DB.
练一练: 已知:如图,点E、F在CD上,且DE=CF,AE=BF,AE∥BF.
①求证:△AEC ≌△BFD.
②你还能证得其他新的结论吗?
练习:
1.如图,AB=AC,AD=AE,∠EAB=∠DAC,问: △ABD与△ACE是否全等?∠D=∠E吗?
2.如图,△ABC中,AB=AC,AD平分∠BAC,
(1)证明:△ABD ≌△ACD.
(2)证明:AD⊥BC
3.如图,已知:点D、E在BC上,
且BD=CE,AD=AE,∠1=∠2,
由此你能得出哪两个三角形全等?请给出证明.
A
B
D
E
C
1
2
通过本节课的学习,你有什么体会?
体会小结:
1.3 探索三角形全等的条件(1)
八年级(上册)
初中数学
1.3 探索三角形全等的条件(1)
问题情境:
(1)如图,△ABC≌△DEF,你能得出哪些结论?
1.3 探索三角形全等的条件(1)
(2)小明想判别△ABC与△DEF是否全等,他逐一检查三角形的三条边、三个角是不是都相等.小红提出了质疑:分别检查三条边、三个角这6个元素固然可以,但是不是可以找到一个更好的方法呢?
问题情境:
1.3 探索三角形全等的条件(1)
讨论交流:
1.当两个三角形的1对边或角相等时,它们全等吗?
2.当两个三角形的2对边或角分别相等时,它们全
等吗?
3.当两个三角形的3对边或角分别相等时,它们全
等吗?
1.3 探索三角形全等的条件(1)
探索活动:
(一)如图,每人用一张长方形纸片剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?
1.3 探索三角形全等的条件(1)
(二)如图,△ABC与△DEF、 △MNP能完全重合吗?
1.3 探索三角形全等的条件(1)
探索活动:
(三)按下列作法,用直尺和圆规作△ABC,使
∠A=∠α,AB=a,AC=b.
作法:
1.作∠MAN =∠α.
2.在射线AM、AN上分别
作线段AB=a,AC=b .
3.连接BC,△ABC就是所求作的三角形.
图形:
a
b
1.3 探索三角形全等的条件(1)
探索活动:
提炼归纳:
基本事实:
两边及其夹角分别相等的两个三角形全等(简写成
“边角边”或“SAS”) .
几何语言:
∵在△ABC和△DEF中,
AB=DE,
∠B=∠E,
BC=EF,
∴ △ABC ≌ △DEF(SAS).
1.3 探索三角形全等的条件(1)
新知应用:
例1 如图,AB =AD,∠BAC =∠DAC.
求证:△ABC ≌ △ADC.
证明:在△ABC和△ADC中,
AB= AD(已知) ,
∠BAC=∠DAC (已知),
AC=AC(公共边),
∴ △ABC ≌ △ADC(SAS).
1.3 探索三角形全等的条件(1)
如图,AB =AD,∠BAC =∠DAC.
变式拓展:
(1)DC =BC吗?
(2)CA平分∠DCB吗?
(3)本例包含哪一种图形变换?
1.3 探索三角形全等的条件(1)
练一练:
如图,AB=AC,AE=AF,
求证:△AFB≌△AEC.
例2 已知:如图,AB、CD相交于点E,且E是AB、CD的中点.
求证:①△AEC≌△BED.
②AC∥DB.
练一练: 已知:如图,点E、F在CD上,且DE=CF,AE=BF,AE∥BF.
①求证:△AEC ≌△BFD.
②你还能证得其他新的结论吗?
练习:
1.如图,AB=AC,AD=AE,∠EAB=∠DAC,问: △ABD与△ACE是否全等?∠D=∠E吗?
2.如图,△ABC中,AB=AC,AD平分∠BAC,
(1)证明:△ABD ≌△ACD.
(2)证明:AD⊥BC
3.如图,已知:点D、E在BC上,
且BD=CE,AD=AE,∠1=∠2,
由此你能得出哪两个三角形全等?请给出证明.
A
B
D
E
C
1
2
通过本节课的学习,你有什么体会?
体会小结:
1.3 探索三角形全等的条件(1)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
