1.3.1集合的基本运算(共23张PPT)
文档属性
| 名称 | 1.3.1集合的基本运算(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 11:27:11 | ||
图片预览







文档简介
(共23张PPT)
1.3.1 集合的基本运算
学习目标
1.理解并集与交集的含义,弄清符号之间的区别与联系;
2.能求两个集合的交集与并集;
3.能使用韦恩图表达集合的基本关系与基本运算.
1
判断下列说法是否正确?
(1)大于3小于11的偶数能组成一个集合;
(2)我国的小河流能组成一个集合;
(3)集合{1,3,5,7}和集合{3,1,5,7}表示同一个集合;
下列集合表示的含义相同吗?
A={y|y=x2 ,x ∈R}
B={x|y=x2 }
2
复习巩固:
解析:(1)正确 {4,6,8,10}
(2)不正确 不满足确定性
(3)正确
不相同,集合A表示的是函数值y的取值范围,而集合B表示的是函数自变量x的取值范围。
思考:
我们知道,实数有加法、减、乘、除运算.集合是否也有类似的运算呢?集合的运算是怎样呢?
思考:
观察下面的集合,类比实数的加法运算,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5}, B={2,4,6},
C={1,2,3,4,5,6};
(2)A={x|x是有理数}, B={x|x是无理数},
C={x|x是实数}.
集合C是由所有属于集合A或者属于集合B的元素组成,这种形式的组合就是集合的并集运算.
请同学们将上述两组实例的共同规律用数学语言表达出来.
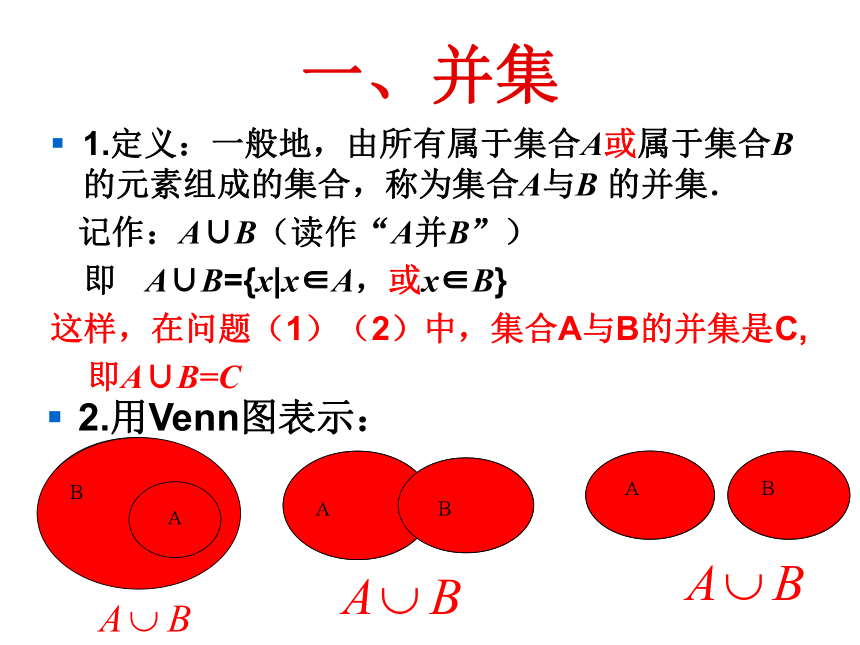
一、并集
1.定义:一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B 的并集.
记作:A∪B(读作“A并B”)
即 A∪B={x|x∈A,或x∈B}
这样,在问题(1)(2)中,集合A与B的并集是C,
即A∪B=C
2.用Venn图表示:
A
B
B
A
A
B
A
B
B
A
A
B
解: A∪B= {4,5,6,8} ∪ {3,5,7,8}
= {3,4,5,6,7,8}
4,6
3,7
5,8
例1 设A={4,5,6,8}, B={3,5,7,8},求A∪B.
为什么两个集合的公共元素在并集中只能出现一次?
说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(根据元素的互异性,重复元素只看成一个元素).
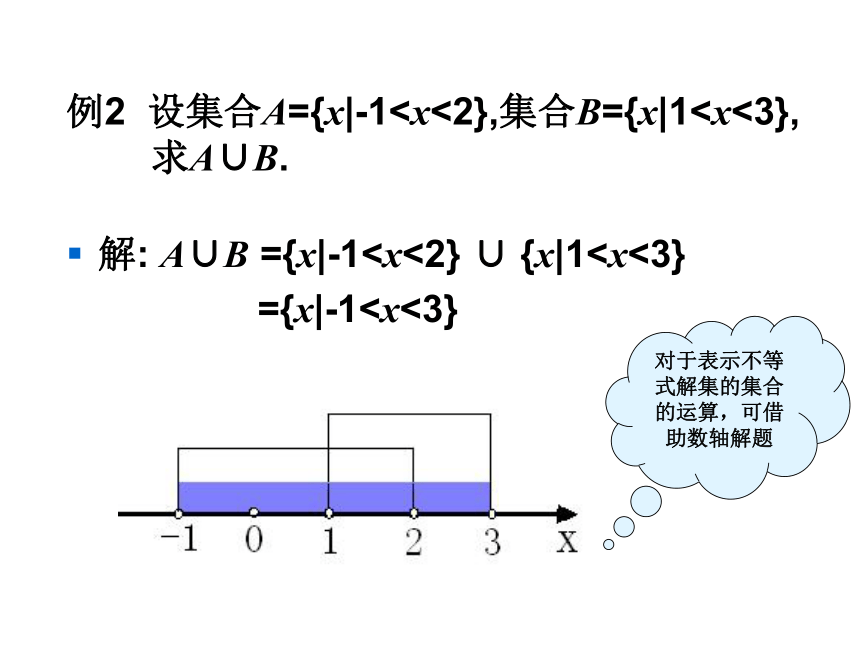
解: A∪B ={x|-1={x|-1例2 设集合A={x|-1求A∪B.
对于表示不等式解集的集合的运算,可借助数轴解题
练一练
(1)设A={1,2},B={2,3,4},
则A∪B= .
(2)设A={x|x<1},B={x|x>2},
则A∪B= .
思考:下列关系式成立吗?说说你的理由.
(1)A∪A= (2)A ∪ =
A
A
(3)A∪B=B∪A
A A∪B;
B A∪B
(4)
并集的运算性质
思考:
由两集合的所有元素合并可得两集合的并集,而由两集合的公共元素组成的集合又会是两集合的一种怎样的运算?
考察:
观察下面集合, 集合A,B与集合C之间有什么关系?
(1)A={2,4,6,8,10},B={3,5,8,12},C={8};
(2)A={x|x是中学今年在校的女同学},
B={x|x是中学今年在校的高一年级同学},
C={x|x是中学今年在校的高一年级女同学}.
由集合A,B的公共元素组合为C,这种形式的组合就是集合的交集运算.
请同学们将上述两组实例的共同规律用数学语言表达出来.
二、交集
1.定义:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集。
记作:A∩B(读作“A交B”)
即 A∩B={x|x∈A,且x∈B}
2.用Venn图表示:
A
B
A
B
A
B
A
二、交集
例3 西南大学东方实验中学开运动会,设
A={x|x是高一年级参加百米赛跑的同学},
B={x|x是高一年级参加跳高比赛的同学},
求A∩B
A ∩ B
高一年级只参加跳高比
赛的同学
高一年级
只参加百
米赛跑的
同学
高一年级既参加百米赛跑又参加
跳高比赛的
同学
解: A ∩ B={x|x是东实高一年级既参加百米赛跑又参加跳高比赛的同学}
①
②
③
练一练
(1)设A={1,2},B={2,3,4},则A∩B= .
(2)设A={x|x<1},B={x|x>2},则A∩B= .
{2}
思考:下列关系式成立吗?
(1)A∩ A = (2)A ∩ =
A
(3)A∩ B =B∩A
巩固练习:
1.设A={3,5,6,8},
B={4,5,7,8},
求 A ∩B, A∪B.
2.设A={x|x2- 4x- 5=0},
B={x|x2=1},
求 A∪B ,A ∩B.
解:A ∩B ={3,5,6,8} ∩ {4,5,7,8}
={5,8}
解:因为A ={x|x2- 4x- 5=0}
={-1,5},
3.A={x|x是等腰三角形},B={x|x是直角三角形}, 求 A ∩B,
A∪B.
解: A ∩B={x|x是等腰直角三角形},
A∪B={x|x是等腰三角形或直角三角形}.
A∪B ={3,5,6,8} ∪{4,5,7,8}
={3,4,5,6,7,8}
所以A∪B={-1,1,5}
A ∩B={-1}
B ={x|x2=1}
={-1,1},
4. 设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )
A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D.
D
变式训练:
1、设集合A={x∈Z|-3B={x∈Z|-1≤x≤3},则A∩B=_____ .
{-1,0,1}
错解: {x|-1≤x<2}
-3
2
3
x
-1
正解: 解:A={x∈Z|-3B={x∈Z|-1≤x≤3}= {-1,0,1,2,3},
A∩B= {-1,0,1}
变式训练:
2、已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是______.
{a |a≤1}
1
x
A
B
a
a>1 (×)
a
B
1
x
A
1
x
A
a<1 (√)
a
B
a=1 (√)
①
②
③
理解两个集合并集与交集的概念.
2. 求两个集合的并集与交集,常用Venn图法和数轴法.
课堂小结
作业
课本14页习题1.3的1,2,3
1.3.1 集合的基本运算
学习目标
1.理解并集与交集的含义,弄清符号之间的区别与联系;
2.能求两个集合的交集与并集;
3.能使用韦恩图表达集合的基本关系与基本运算.
1
判断下列说法是否正确?
(1)大于3小于11的偶数能组成一个集合;
(2)我国的小河流能组成一个集合;
(3)集合{1,3,5,7}和集合{3,1,5,7}表示同一个集合;
下列集合表示的含义相同吗?
A={y|y=x2 ,x ∈R}
B={x|y=x2 }
2
复习巩固:
解析:(1)正确 {4,6,8,10}
(2)不正确 不满足确定性
(3)正确
不相同,集合A表示的是函数值y的取值范围,而集合B表示的是函数自变量x的取值范围。
思考:
我们知道,实数有加法、减、乘、除运算.集合是否也有类似的运算呢?集合的运算是怎样呢?
思考:
观察下面的集合,类比实数的加法运算,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5}, B={2,4,6},
C={1,2,3,4,5,6};
(2)A={x|x是有理数}, B={x|x是无理数},
C={x|x是实数}.
集合C是由所有属于集合A或者属于集合B的元素组成,这种形式的组合就是集合的并集运算.
请同学们将上述两组实例的共同规律用数学语言表达出来.
一、并集
1.定义:一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B 的并集.
记作:A∪B(读作“A并B”)
即 A∪B={x|x∈A,或x∈B}
这样,在问题(1)(2)中,集合A与B的并集是C,
即A∪B=C
2.用Venn图表示:
A
B
B
A
A
B
A
B
B
A
A
B
解: A∪B= {4,5,6,8} ∪ {3,5,7,8}
= {3,4,5,6,7,8}
4,6
3,7
5,8
例1 设A={4,5,6,8}, B={3,5,7,8},求A∪B.
为什么两个集合的公共元素在并集中只能出现一次?
说明:两个集合求并集,结果还是一个集合,是由集合A与B 的所有元素组成的集合(根据元素的互异性,重复元素只看成一个元素).
解: A∪B ={x|-1
对于表示不等式解集的集合的运算,可借助数轴解题
练一练
(1)设A={1,2},B={2,3,4},
则A∪B= .
(2)设A={x|x<1},B={x|x>2},
则A∪B= .
思考:下列关系式成立吗?说说你的理由.
(1)A∪A= (2)A ∪ =
A
A
(3)A∪B=B∪A
A A∪B;
B A∪B
(4)
并集的运算性质
思考:
由两集合的所有元素合并可得两集合的并集,而由两集合的公共元素组成的集合又会是两集合的一种怎样的运算?
考察:
观察下面集合, 集合A,B与集合C之间有什么关系?
(1)A={2,4,6,8,10},B={3,5,8,12},C={8};
(2)A={x|x是中学今年在校的女同学},
B={x|x是中学今年在校的高一年级同学},
C={x|x是中学今年在校的高一年级女同学}.
由集合A,B的公共元素组合为C,这种形式的组合就是集合的交集运算.
请同学们将上述两组实例的共同规律用数学语言表达出来.
二、交集
1.定义:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集。
记作:A∩B(读作“A交B”)
即 A∩B={x|x∈A,且x∈B}
2.用Venn图表示:
A
B
A
B
A
B
A
二、交集
例3 西南大学东方实验中学开运动会,设
A={x|x是高一年级参加百米赛跑的同学},
B={x|x是高一年级参加跳高比赛的同学},
求A∩B
A ∩ B
高一年级只参加跳高比
赛的同学
高一年级
只参加百
米赛跑的
同学
高一年级既参加百米赛跑又参加
跳高比赛的
同学
解: A ∩ B={x|x是东实高一年级既参加百米赛跑又参加跳高比赛的同学}
①
②
③
练一练
(1)设A={1,2},B={2,3,4},则A∩B= .
(2)设A={x|x<1},B={x|x>2},则A∩B= .
{2}
思考:下列关系式成立吗?
(1)A∩ A = (2)A ∩ =
A
(3)A∩ B =B∩A
巩固练习:
1.设A={3,5,6,8},
B={4,5,7,8},
求 A ∩B, A∪B.
2.设A={x|x2- 4x- 5=0},
B={x|x2=1},
求 A∪B ,A ∩B.
解:A ∩B ={3,5,6,8} ∩ {4,5,7,8}
={5,8}
解:因为A ={x|x2- 4x- 5=0}
={-1,5},
3.A={x|x是等腰三角形},B={x|x是直角三角形}, 求 A ∩B,
A∪B.
解: A ∩B={x|x是等腰直角三角形},
A∪B={x|x是等腰三角形或直角三角形}.
A∪B ={3,5,6,8} ∪{4,5,7,8}
={3,4,5,6,7,8}
所以A∪B={-1,1,5}
A ∩B={-1}
B ={x|x2=1}
={-1,1},
4. 设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )
A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D.
D
变式训练:
1、设集合A={x∈Z|-3
{-1,0,1}
错解: {x|-1≤x<2}
-3
2
3
x
-1
正解: 解:A={x∈Z|-3
A∩B= {-1,0,1}
变式训练:
2、已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是______.
{a |a≤1}
1
x
A
B
a
a>1 (×)
a
B
1
x
A
1
x
A
a<1 (√)
a
B
a=1 (√)
①
②
③
理解两个集合并集与交集的概念.
2. 求两个集合的并集与交集,常用Venn图法和数轴法.
课堂小结
作业
课本14页习题1.3的1,2,3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
