苏科版九年级数学上册 2.4 圆周角(共16张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.4 圆周角(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 08:15:45 | ||
图片预览



文档简介
(共16张PPT)
圆周角
一
2.4 圆周角(2)
请你画一画
有一个圆形模具,现在只有一个直角三角板,请你找出它的圆心.
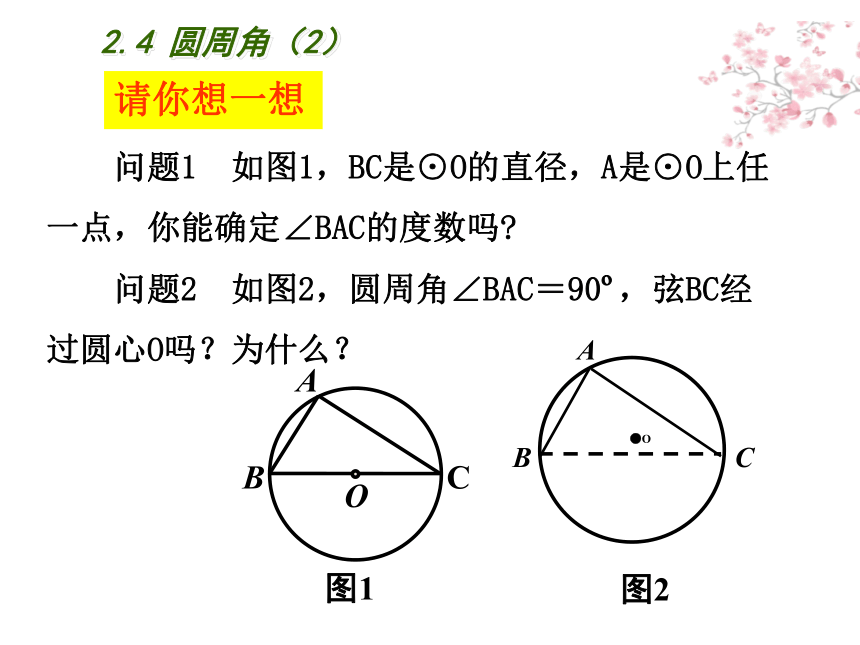
问题1 如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
B
A
O
C
图1
问题2 如图2,圆周角∠BAC=90 ,弦BC经过圆心O吗?为什么?
●O
B
C
A
图2
2.4 圆周角(2)
请你想一想
2.4 圆周角(2)
请你议一议
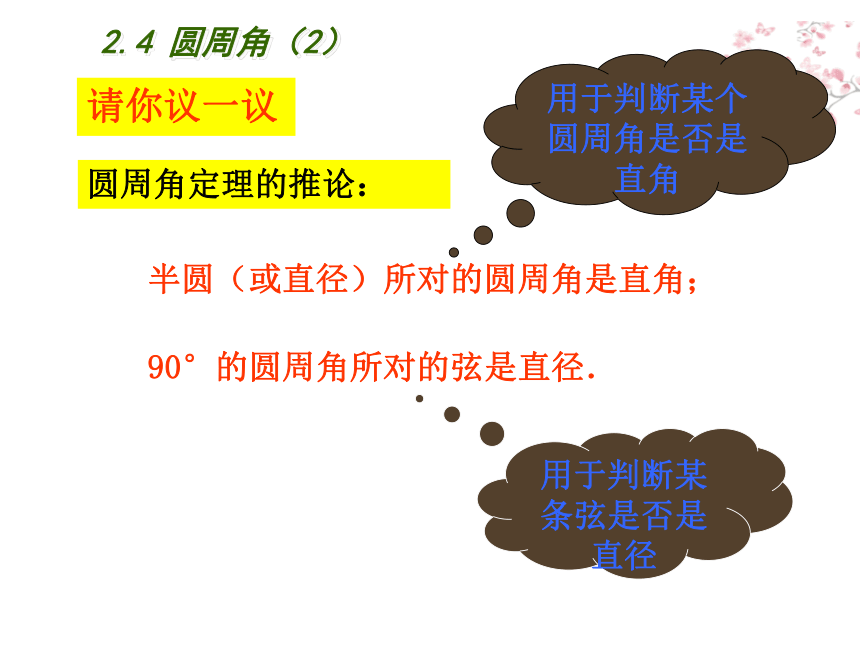
圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;
用于判断某个圆周角是否是直角
用于判断某条弦是否是直径
90°的圆周角所对的弦是直径.
2.4 圆周角(2)
典型例题
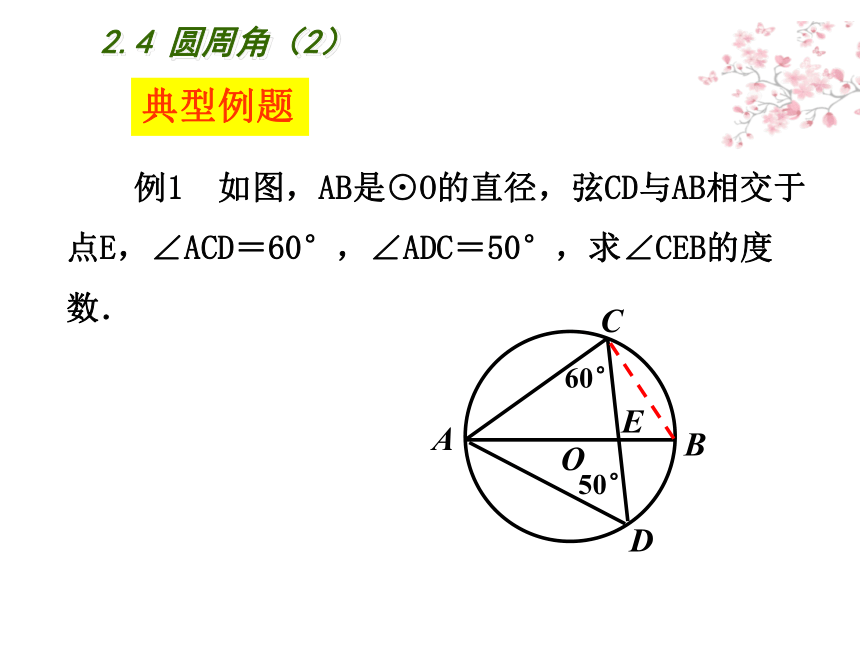
例1 如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.
A
B
D
C
O
E
60°
50°
2.4 圆周角(2)
例2 已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,AE=AB,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.
(
(
典型例题
2.4 圆周角(2)
典型例题
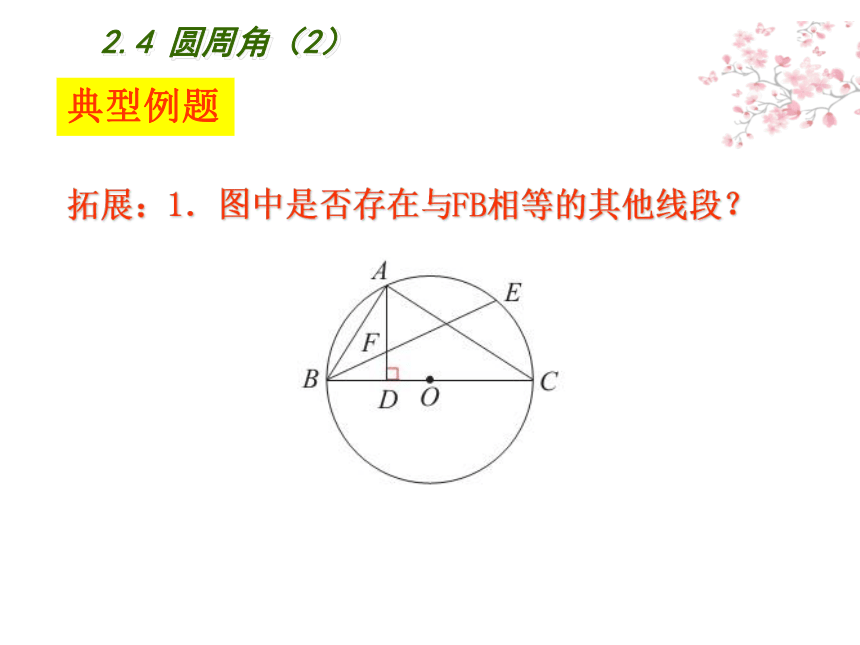
拓展:1.图中是否存在与FB相等的其他线段?
2.4 圆周角(2)
典型例题
拓展:2.在例2中,若点E与点A在直径BC的两侧,BE交AD的延长线于点F,其余条件不变(如下图),例2中的结论还成立吗?
2.4 圆周角(2)
现在你会了吗?
“有一个圆形模具,现在只有一个直角三角板,请你找出它的圆心”.你现在能解决吗?
2.4 圆周角(2)
巩固练习
1.如图,AB是⊙O的直径,∠A=10°,
则∠ABC=________.
2.4 圆周角(2)
巩固练习
2.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: .
2.4 圆周角(2)
巩固练习
3.如图,AE是⊙O的直径,△ABC的顶点都在⊙O上,AD是△ABC的高,△ABE和 △ADC相似吗?为什么?
2.4 圆周角(2)
拓展提升
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠C=45°,求这个人工湖的直径.
2.4 圆周角(2)
请你议一议
这节课你有哪些收获?
今天我们学习了圆中有哪些常用辅助线?
课后作业
课本P58第1、2、3.
2.4 圆周角(2)
2.4 圆周角(2)
圆周角
一
2.4 圆周角(2)
请你画一画
有一个圆形模具,现在只有一个直角三角板,请你找出它的圆心.
问题1 如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
B
A
O
C
图1
问题2 如图2,圆周角∠BAC=90 ,弦BC经过圆心O吗?为什么?
●O
B
C
A
图2
2.4 圆周角(2)
请你想一想
2.4 圆周角(2)
请你议一议
圆周角定理的推论:
半圆(或直径)所对的圆周角是直角;
用于判断某个圆周角是否是直角
用于判断某条弦是否是直径
90°的圆周角所对的弦是直径.
2.4 圆周角(2)
典型例题
例1 如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.
A
B
D
C
O
E
60°
50°
2.4 圆周角(2)
例2 已知:BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,AE=AB,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.
(
(
典型例题
2.4 圆周角(2)
典型例题
拓展:1.图中是否存在与FB相等的其他线段?
2.4 圆周角(2)
典型例题
拓展:2.在例2中,若点E与点A在直径BC的两侧,BE交AD的延长线于点F,其余条件不变(如下图),例2中的结论还成立吗?
2.4 圆周角(2)
现在你会了吗?
“有一个圆形模具,现在只有一个直角三角板,请你找出它的圆心”.你现在能解决吗?
2.4 圆周角(2)
巩固练习
1.如图,AB是⊙O的直径,∠A=10°,
则∠ABC=________.
2.4 圆周角(2)
巩固练习
2.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状: .
2.4 圆周角(2)
巩固练习
3.如图,AE是⊙O的直径,△ABC的顶点都在⊙O上,AD是△ABC的高,△ABE和 △ADC相似吗?为什么?
2.4 圆周角(2)
拓展提升
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠C=45°,求这个人工湖的直径.
2.4 圆周角(2)
请你议一议
这节课你有哪些收获?
今天我们学习了圆中有哪些常用辅助线?
课后作业
课本P58第1、2、3.
2.4 圆周角(2)
2.4 圆周角(2)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
