2.1.1等式性质与不等式性质(共22张PPT)
文档属性
| 名称 | 2.1.1等式性质与不等式性质(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 20:00:15 | ||
图片预览







文档简介
(共22张PPT)
§2.1 等式性质与不等式性质(1)
第二章 一元二次函数、方程和不等式
1.会用作差法比较两实数的大小;
2.掌握一个基本不等式及证明;
3.会用不等式(组)表示实际问题中的不等关系;
学习目标:
不等式表示不等关系
【问题1】你能用不等式或不等式组表示下列不等关系吗?
(2)某品牌牛奶质量检查规定:脂肪含量f应不少于2.5%,
蛋白质含量p应不少于2.3%;
(1)某路段限速40km/h;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短。
【练习】用不等式或不等式组表示下面的不等关系.
解 0(2)a与b的和是非负实数;
解 a+b≥0;
(1)某高速公路规定通过车辆的车货总高度h(单位:m)从地面算起不能超过4 m;
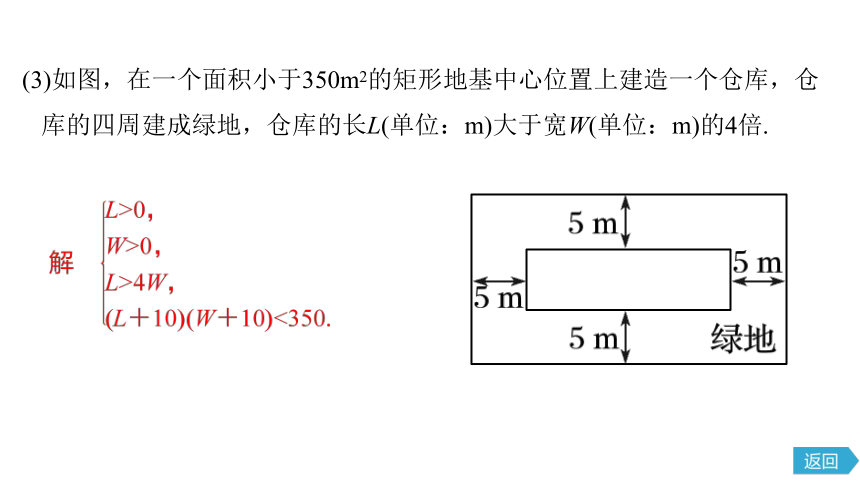
(3)如图,在一个面积小于350m2的矩形地基中心位置上建造一个仓库,仓
库的四周建成绿地,仓库的长L(单位:m)大于宽W(单位:m)的4倍.
【启示】以上我们根据实际问题所蕴含的不等关系抽象出了不
等式(组),接着就可以用不等式研究相应的问题了。
不等式表示不等关系
不等式表示不等关系
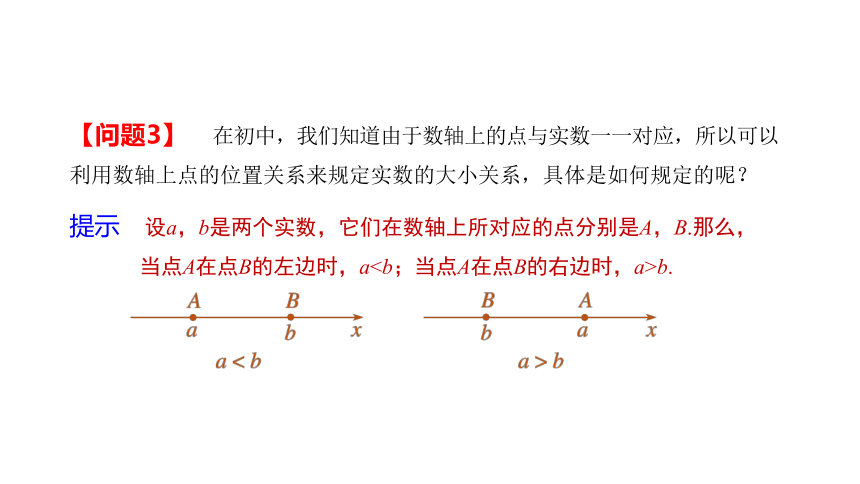
【问题3】 在初中,我们知道由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系,具体是如何规定的呢?
提示 设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,
当点A在点B的左边时,ab.
依据 a>b __________
a=b ___________
a结论 要比较两个实数的大小,可以转化为比较它们的 与 的大小
a-b>0
a-b=0
a-b<0
差
0
不等式最基本的性质
例1 比较2x2+5x+3与x2+4x+2的大小.
解 (2x2+5x+3)-(x2+4x+2)=x2+x+1
∴(2x2+5x+3)-(x2+4x+2)>0,
∴2x2+5x+3>x2+4x+2.
反思感悟 作差法比较两个实数大小的基本步骤
跟踪训练2 比较(x+3)(x+7)和(x+4)(x+6)的大小.
解 因为(x+3)(x+7)-(x+4)(x+6)
=(x2+10x+21)-(x2+10x+24)=-3<0,
所以(x+3)(x+7)<(x+4)(x+6).
【问题4】如图是由在北京召开第24届国际数学家大会的会标抽象出来的图形,你能比较
大正方形ABCD与四个相同的直角三角形的面积之和的大小吗?从中你能得出哪
个不等式?它们之间有可能相等吗?如果相等,则应该满足什么条件呢?
提示 正方形的边长为 .
这样,4个直角三角形的面积和为2ab,正方形的面积为a2+b2,
由于正方形ABCD的面积大于4个直角三角形的面积和,我们就得到了一个不等式a2+b2>2ab.
当直角三角形变为等腰直角三角形,
即a=b时,正方形EFGH缩为一个点,这时有a2+b2=2ab.
于是就有a2+b2≥2ab.
证明a2+b2-2ab=(a-b)2.
因为 a,b∈R,(a-b)2≥0,
当且仅当a=b时,等号成立,
所以a2+b2-2ab≥0.
因此,由两个实数大小比较的基本事实,得a2+b2≥2ab,
当且仅当a=b时,等号成立.
设a,b是任意实数,则a2+b2≥2ab,
当且仅当a=b时,等号成立.
一个重要不等式
例2 已知a>0,b>0.
(1)求证:a2+3b2≥2b(a+b);
证明 ①∵a2+3b2-2b(a+b)=a2-2ab+b2=(a-b)2≥0,
当且仅当a=b时,等号成立,
∴a2+3b2≥2b(a+b).
②∵a2+b2≥2ab,当且仅当a=b时,等号成立,
∴a2+b2+2b2≥2ab+2b2=2b(a+b)
例2 已知a>0,b>0.
(1)求证:a2+3b2≥2b(a+b);
(2)求证:a3+b3≥ab2+a2b.
证明 因为a3+b3-(ab2+a2b)=a3+b3-ab2-a2b=a3-ab2+b3-a2b
=a(a2-b2)+b(b2-a2)=(a2-b2)(a-b)=(a+b)(a-b)2,
因为a>0,b>0,所以(a+b)(a-b)2≥0,
当且仅当a=b时,等号成立,
所以a3+b3-(ab2+a2b)≥0,所以a3+b3≥ab2+a2b.
【反思1】比较两个数的大小关系,最基本的方法是利用作差法,通过因式分解或配方
的方法,把“差”转化成几个因式乘积的形式, 通过逻辑推理得到每一个因
式的符号,从而判定两个数的大小关系,通过逻辑推理进行证明.
【反思2】也可以考虑用重要不等式.
跟踪训练3 已知a>0,求证:a+ ≥2.
证明 方法一 利用a2+b2≥2ab.
当且仅当a=1时,等号成立.
1.知识清单:
(1)用不等式(组)表示不等关系.
(2)作差法比较大小.
(3)重要不等式.
2.方法归纳:作差法.
3.常见误区:实际问题中变量的实际意义.
课堂小结
作业:
课本p40 练习 2. 3
课本p42 习题2-1 2. 3
§2.1 等式性质与不等式性质(1)
第二章 一元二次函数、方程和不等式
1.会用作差法比较两实数的大小;
2.掌握一个基本不等式及证明;
3.会用不等式(组)表示实际问题中的不等关系;
学习目标:
不等式表示不等关系
【问题1】你能用不等式或不等式组表示下列不等关系吗?
(2)某品牌牛奶质量检查规定:脂肪含量f应不少于2.5%,
蛋白质含量p应不少于2.3%;
(1)某路段限速40km/h;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短。
【练习】用不等式或不等式组表示下面的不等关系.
解 0
解 a+b≥0;
(1)某高速公路规定通过车辆的车货总高度h(单位:m)从地面算起不能超过4 m;
(3)如图,在一个面积小于350m2的矩形地基中心位置上建造一个仓库,仓
库的四周建成绿地,仓库的长L(单位:m)大于宽W(单位:m)的4倍.
【启示】以上我们根据实际问题所蕴含的不等关系抽象出了不
等式(组),接着就可以用不等式研究相应的问题了。
不等式表示不等关系
不等式表示不等关系
【问题3】 在初中,我们知道由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系,具体是如何规定的呢?
提示 设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,
当点A在点B的左边时,a
依据 a>b __________
a=b ___________
a结论 要比较两个实数的大小,可以转化为比较它们的 与 的大小
a-b>0
a-b=0
a-b<0
差
0
不等式最基本的性质
例1 比较2x2+5x+3与x2+4x+2的大小.
解 (2x2+5x+3)-(x2+4x+2)=x2+x+1
∴(2x2+5x+3)-(x2+4x+2)>0,
∴2x2+5x+3>x2+4x+2.
反思感悟 作差法比较两个实数大小的基本步骤
跟踪训练2 比较(x+3)(x+7)和(x+4)(x+6)的大小.
解 因为(x+3)(x+7)-(x+4)(x+6)
=(x2+10x+21)-(x2+10x+24)=-3<0,
所以(x+3)(x+7)<(x+4)(x+6).
【问题4】如图是由在北京召开第24届国际数学家大会的会标抽象出来的图形,你能比较
大正方形ABCD与四个相同的直角三角形的面积之和的大小吗?从中你能得出哪
个不等式?它们之间有可能相等吗?如果相等,则应该满足什么条件呢?
提示 正方形的边长为 .
这样,4个直角三角形的面积和为2ab,正方形的面积为a2+b2,
由于正方形ABCD的面积大于4个直角三角形的面积和,我们就得到了一个不等式a2+b2>2ab.
当直角三角形变为等腰直角三角形,
即a=b时,正方形EFGH缩为一个点,这时有a2+b2=2ab.
于是就有a2+b2≥2ab.
证明a2+b2-2ab=(a-b)2.
因为 a,b∈R,(a-b)2≥0,
当且仅当a=b时,等号成立,
所以a2+b2-2ab≥0.
因此,由两个实数大小比较的基本事实,得a2+b2≥2ab,
当且仅当a=b时,等号成立.
设a,b是任意实数,则a2+b2≥2ab,
当且仅当a=b时,等号成立.
一个重要不等式
例2 已知a>0,b>0.
(1)求证:a2+3b2≥2b(a+b);
证明 ①∵a2+3b2-2b(a+b)=a2-2ab+b2=(a-b)2≥0,
当且仅当a=b时,等号成立,
∴a2+3b2≥2b(a+b).
②∵a2+b2≥2ab,当且仅当a=b时,等号成立,
∴a2+b2+2b2≥2ab+2b2=2b(a+b)
例2 已知a>0,b>0.
(1)求证:a2+3b2≥2b(a+b);
(2)求证:a3+b3≥ab2+a2b.
证明 因为a3+b3-(ab2+a2b)=a3+b3-ab2-a2b=a3-ab2+b3-a2b
=a(a2-b2)+b(b2-a2)=(a2-b2)(a-b)=(a+b)(a-b)2,
因为a>0,b>0,所以(a+b)(a-b)2≥0,
当且仅当a=b时,等号成立,
所以a3+b3-(ab2+a2b)≥0,所以a3+b3≥ab2+a2b.
【反思1】比较两个数的大小关系,最基本的方法是利用作差法,通过因式分解或配方
的方法,把“差”转化成几个因式乘积的形式, 通过逻辑推理得到每一个因
式的符号,从而判定两个数的大小关系,通过逻辑推理进行证明.
【反思2】也可以考虑用重要不等式.
跟踪训练3 已知a>0,求证:a+ ≥2.
证明 方法一 利用a2+b2≥2ab.
当且仅当a=1时,等号成立.
1.知识清单:
(1)用不等式(组)表示不等关系.
(2)作差法比较大小.
(3)重要不等式.
2.方法归纳:作差法.
3.常见误区:实际问题中变量的实际意义.
课堂小结
作业:
课本p40 练习 2. 3
课本p42 习题2-1 2. 3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
