2.1.2等式性质与不等式性质(2)(共29张PPT)
文档属性
| 名称 | 2.1.2等式性质与不等式性质(2)(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 739.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 20:00:57 | ||
图片预览








文档简介
(共29张PPT)
§2.1 等式性质与不等式性质(2)
第二章 一元二次函数、方程和不等式
学习目标:
1、等式性质与不等式的性质
2、利用不等式的性质证明不等式
3、利用不等式的性质求代数式的取值范围
依据 a>b __________
a=b ___________
a结论 要比较两个实数的大小,可以转化为比较它们的 与 的大小
a-b>0
a-b=0
a-b<0
差
0
不等式最基本的性质
复习巩固
设a,b是任意实数,则a2+b2≥2ab,
当且仅当a=b时,等号成立.
一个重要的不等式
复习巩固
一、等式的性质
(1)如果a=b,那么b=a;
(2)如果a=b,b=c,那么a=c;
(3)如果a=b,那么a±c=b±c;
(4)如果a=b,那么ac=bc;
(5)如果a=b,c≠0,那么 .
二、不等式的性质
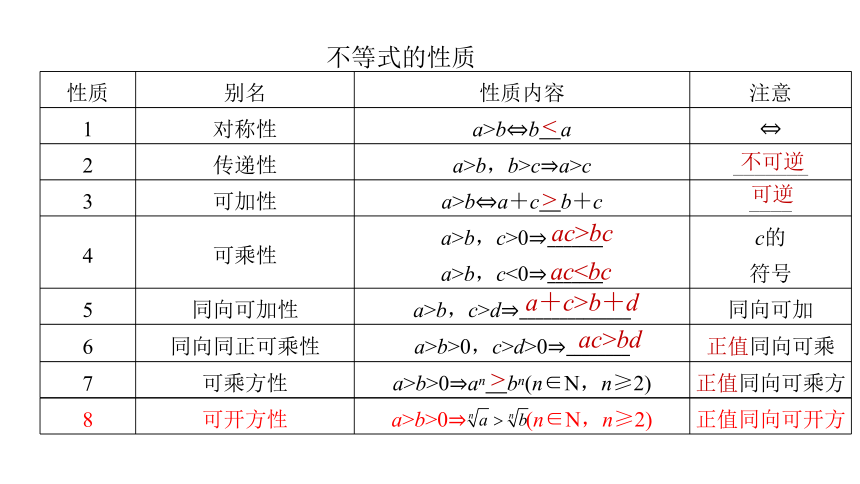
不等式的性质
性质 别名 性质内容 注意
1 对称性 a>b b a
2 传递性 a>b,b>c a>c _______
3 可加性 a>b a+c b+c ____
4 可乘性 a>b,c>0 _______ a>b,c<0 _______ c的
符号
5 同向可加性 a>b,c>d ______________ 同向可加
6 同向同正可乘性 a>b>0,c>d>0 ________ 正值同向可乘
7 可乘方性 a>b>0 an bn(n∈N,n≥2) 正值同向可乘方
<
不可逆
>
可逆
ac>bc
aca+c>b+d
ac>bd
>
8 可开方性 a>b>0 (n∈N,n≥2) 正值同向可开方
【例2】对于实数a,b,c,下列命题中的真命题是
A.若a>b,则ac2>bc2
√
解析 方法一 ∵c2≥0,∴c=0时,有ac2=bc2,故A为假命题;
∵a>b,∴a>0且b<0,故D为真命题.
方法二 特殊值排除法.
取c=0,则ac2=bc2,故A错.
【反思】 利用不等式的性质判断命题真假的注意点
(1)运用不等式的性质判断时,要注意不等式成立的条件,
不要弱化条件,尤其是不能想当然随意捏造性质.
(2)解有关不等式的选择题时,也可采用特殊值法进行排除,
注意取值一定要遵循如下原则:一是满足题设条件;二是
取值要简单,便于验证计算.
跟踪训练1 (多选)若 <0,则下面四个不等式成立的有
A.|a|>|b| B.aC.a+bb3
√
√
a+b<0,ab>0,则a+ba3>b3,D正确.
三、利用不等式的性质证明不等式
∵c>a>b>0,
∴a-b>0,c-a>0,c-b>0,
因为c>a>b>0,所以c-a>0,c-b>0.
【证明3】 因为c>a>b>0,
所以0【反思】(1)利用不等式的性质对不等式的证明其实质就是利用
性质对不等式进行变形,变形要等价,同时要注意
性质适用的 前提条件.
(2)用作差法证明不等式和用作差法比较大小的方法原
理一样,变形后判断符号时要注意充分利用题目中
的条件.
∵a>b>0,c<0,
∴ab>0,b-a<0,c(b-a)>0,
【证明2】 ∵a>b>0,
四、利用不等式性质求代数式的取值范围
【例4】 已知-6解 因为-6②当-6所以-12<2a<16,
所以-10<2a+b<19.
又因为-3<-b<-2,
所以-9【例5】已知-1【反思】利用不等式的性质求取值范围的策略
(1)建立待求范围的整体与已知范围的整体的关系,最后利
用一次不等式的性质进行运算,求得待求的范围.
(2)同向不等式的两边可以相加,这种转化不是等价变形,
如果在解题过程中多次使用这种转化,就有可能扩大其
取值范围.
跟踪训练3 已知1取值范围是_______.
解析 ∵3∴1-4-31.知识点:
(1)等式的性质.
(2)不等式的性质及其应用.
2.方法归纳:作商比较法、乘方比较法.
3.误区:注意不等式性质的单向性或双向性,即每条性质是否具有可逆性.
课堂小结
作业:
课本p42 练习 1. 2
课本p42 习题2-1 4 --- 12
本课结束
§2.1 等式性质与不等式性质(2)
第二章 一元二次函数、方程和不等式
学习目标:
1、等式性质与不等式的性质
2、利用不等式的性质证明不等式
3、利用不等式的性质求代数式的取值范围
依据 a>b __________
a=b ___________
a结论 要比较两个实数的大小,可以转化为比较它们的 与 的大小
a-b>0
a-b=0
a-b<0
差
0
不等式最基本的性质
复习巩固
设a,b是任意实数,则a2+b2≥2ab,
当且仅当a=b时,等号成立.
一个重要的不等式
复习巩固
一、等式的性质
(1)如果a=b,那么b=a;
(2)如果a=b,b=c,那么a=c;
(3)如果a=b,那么a±c=b±c;
(4)如果a=b,那么ac=bc;
(5)如果a=b,c≠0,那么 .
二、不等式的性质
不等式的性质
性质 别名 性质内容 注意
1 对称性 a>b b a
2 传递性 a>b,b>c a>c _______
3 可加性 a>b a+c b+c ____
4 可乘性 a>b,c>0 _______ a>b,c<0 _______ c的
符号
5 同向可加性 a>b,c>d ______________ 同向可加
6 同向同正可乘性 a>b>0,c>d>0 ________ 正值同向可乘
7 可乘方性 a>b>0 an bn(n∈N,n≥2) 正值同向可乘方
<
不可逆
>
可逆
ac>bc
ac
ac>bd
>
8 可开方性 a>b>0 (n∈N,n≥2) 正值同向可开方
【例2】对于实数a,b,c,下列命题中的真命题是
A.若a>b,则ac2>bc2
√
解析 方法一 ∵c2≥0,∴c=0时,有ac2=bc2,故A为假命题;
∵a>b,∴a>0且b<0,故D为真命题.
方法二 特殊值排除法.
取c=0,则ac2=bc2,故A错.
【反思】 利用不等式的性质判断命题真假的注意点
(1)运用不等式的性质判断时,要注意不等式成立的条件,
不要弱化条件,尤其是不能想当然随意捏造性质.
(2)解有关不等式的选择题时,也可采用特殊值法进行排除,
注意取值一定要遵循如下原则:一是满足题设条件;二是
取值要简单,便于验证计算.
跟踪训练1 (多选)若 <0,则下面四个不等式成立的有
A.|a|>|b| B.a
√
√
a+b<0,ab>0,则a+b
三、利用不等式的性质证明不等式
∵c>a>b>0,
∴a-b>0,c-a>0,c-b>0,
因为c>a>b>0,所以c-a>0,c-b>0.
【证明3】 因为c>a>b>0,
所以0
性质对不等式进行变形,变形要等价,同时要注意
性质适用的 前提条件.
(2)用作差法证明不等式和用作差法比较大小的方法原
理一样,变形后判断符号时要注意充分利用题目中
的条件.
∵a>b>0,c<0,
∴ab>0,b-a<0,c(b-a)>0,
【证明2】 ∵a>b>0,
四、利用不等式性质求代数式的取值范围
【例4】 已知-6
所以-10<2a+b<19.
又因为-3<-b<-2,
所以-9
(1)建立待求范围的整体与已知范围的整体的关系,最后利
用一次不等式的性质进行运算,求得待求的范围.
(2)同向不等式的两边可以相加,这种转化不是等价变形,
如果在解题过程中多次使用这种转化,就有可能扩大其
取值范围.
跟踪训练3 已知1
解析 ∵3
(1)等式的性质.
(2)不等式的性质及其应用.
2.方法归纳:作商比较法、乘方比较法.
3.误区:注意不等式性质的单向性或双向性,即每条性质是否具有可逆性.
课堂小结
作业:
课本p42 练习 1. 2
课本p42 习题2-1 4 --- 12
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
