2021_2022学年新教材高中数学2.3.4圆与圆的位置关系(word含解析)
文档属性
| 名称 | 2021_2022学年新教材高中数学2.3.4圆与圆的位置关系(word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 20:27:56 | ||
图片预览



文档简介
圆与圆的位置关系
(建议用时:40分钟)
基础练
一、选择题
1.圆x2+y2=4与圆x2+y2-2x+4y-4=0的位置关系为( )
A.相离 B.相交 C.相切 D.内含
2.圆x2+4x+y2=0与圆(x-2)2+(y-3)2=r2有三条公切线,则半径r=( )
A.5 B.4 C.3 D.2
3.若圆C:x2+(y-4)2=18与圆D:(x-1)2+(y-1)2=r2的公共弦长为6,则圆D的半径为( )
A.5 B.2 C.2 D.2
4.半径为5且与圆x2+y2-6x+8y=0相切于原点的圆的方程为( )
A.x2+y2-6x-8y=0
B.x2+y2+6x-8y=0
C.x2+y2+6x+8y=0
D.x2+y2-6x-8y=0或x2+y2-6x+8y=0
5.已知半径为1 cm的两圆外切,半径为2 cm且和这两圆都相切的圆共有( )
A.3个 B.4个 C.2个 D.5个
二、填空题
6.已知圆C的圆心为(2,1),若圆C与圆M:x2+y2-3x=0的公共弦所在直线过点(5,-2),则圆C的方程为________.
7.已知点P在圆x2+y2-8x-4y+11=0上,点Q在圆x2+y2+4x+2y+1=0上,则|PQ|的最小值是________.
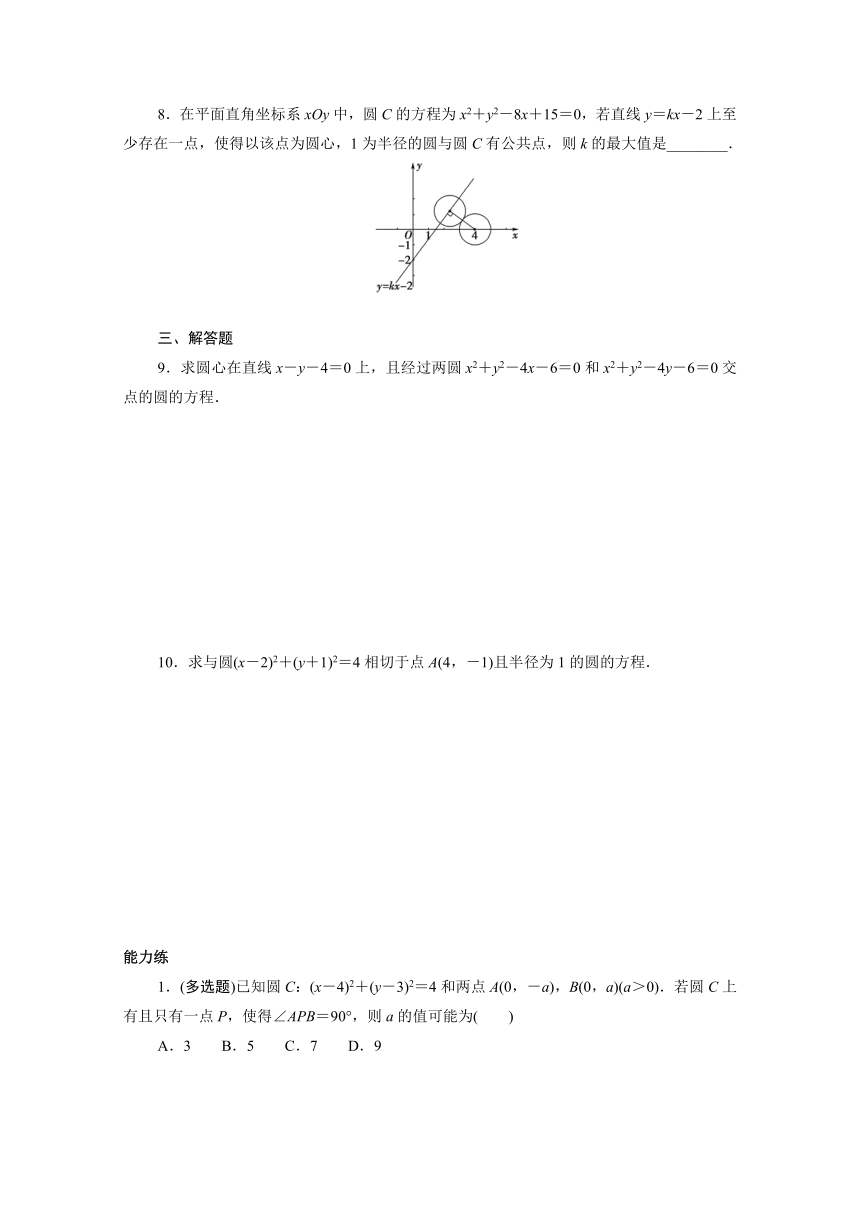
8.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
三、解答题
9.求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0交点的圆的方程.
10.求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
能力练
1.(多选题)已知圆C:(x-4)2+(y-3)2=4和两点A(0,-a),B(0,a)(a>0).若圆C上有且只有一点P,使得∠APB=90°,则a的值可能为( )
A.3 B.5 C.7 D.9
2.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
A.4 B.4 C.8 D.8
3.在直角坐标系xOy中,点A(x1,y1)和点B(x2,y2)是单位圆x2+y2=1上两点,|AB|=1,则∠AOB=_____________,|y1+2|+|y2+2|的最大值为________.
4.与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是________.
拓展
在平面直角坐标系xOy中,已知圆M:(x-3)2+(y-4)2=4及其上一点A.
(1)求|OA|的最大值;
(2)设A(3,2),点T在x轴上.若圆M上存在两点P和Q,使得+=,求点T的横坐标的取值范围.
参考答案:
基础练
一、选择题
1.圆x2+y2=4与圆x2+y2-2x+4y-4=0的位置关系为( )
A.相离 B.相交 C.相切 D.内含
B [圆x2+y2=4的圆心坐标为(0,0),半径为2,圆x2+y2-2x+4y-4=0,即(x-1)2+(y+2)2=9,圆心坐标为(1,-2),半径为3,两圆的圆心距为=,半径和为5,半径差的绝对值为1,∵1<<5,∴两圆相交.]
2.圆x2+4x+y2=0与圆(x-2)2+(y-3)2=r2有三条公切线,则半径r=( )
A.5 B.4 C.3 D.2
C [两圆的圆心分别为(-2,0),(2,3),半径分别为2,r,由于两圆有三条公切线,所以两圆相外切,∴=2+r,即5=2+r,∴r=3.]
3.若圆C:x2+(y-4)2=18与圆D:(x-1)2+(y-1)2=r2的公共弦长为6,则圆D的半径为( )
A.5 B.2 C.2 D.2
D [两圆方程相减得2x-6y=4-r2,又由圆C的方程为x2+(y-4)2=18,其圆心为(0,4),半径r=3,两圆的公共弦长为6,则点(0,4)在直线2x-6y=4-r2上,则有2×0-6×4=4-r2,r2=28,r=2.]
4.半径为5且与圆x2+y2-6x+8y=0相切于原点的圆的方程为( )
A.x2+y2-6x-8y=0
B.x2+y2+6x-8y=0
C.x2+y2+6x+8y=0
D.x2+y2-6x-8y=0或x2+y2-6x+8y=0
B [已知圆的圆心为(3,-4),半径为5,所求圆的半径也为5,由两圆相切于原点,知所求圆的圆心与已知圆的圆心关于原点对称,即为(-3,4),可知选B.]
5.已知半径为1 cm的两圆外切,半径为2 cm且和这两圆都相切的圆共有( )
A.3个 B.4个 C.2个 D.5个
D [要全面分析所有的情况,包括都外切,都内切,一内切一外切.这样的圆共有5个,如图,它们是圆A、圆B、圆C、圆D、圆E.]
二、填空题
6.已知圆C的圆心为(2,1),若圆C与圆M:x2+y2-3x=0的公共弦所在直线过点(5,-2),则圆C的方程为________.
(x-2)2+(y-1)2=4 [设圆C的半径为r,则圆C的方程为(x-2)2+(y-1)2=r2,即x2+y2-4x-2y+5-r2=0.将圆C与圆M的方程相减得公共弦所在直线的方程为x+2y-5+r2=0.因为该直线过点(5,-2),所以r2=4.
故圆C的方程为(x-2)2+(y-1)2=4.]
7.已知点P在圆x2+y2-8x-4y+11=0上,点Q在圆x2+y2+4x+2y+1=0上,则|PQ|的最小值是________.
3-5 [两圆的圆心和半径分别为C1(4,2),r1=3,
C2(-2,-1),r2=2,|C1C2|=3,|C1C2|>r1+r2,∴两圆外离.
∴|PQ|min=|C1C2|-r1-r2=3-3-2=3-5.]
8.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
[圆C:(x-4)2+y2=1,如图,要满足直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,只需保证圆心C到y=kx-2的距离小于或等于2,
即≤2,解得0≤k≤.∴kmax=.]
三、解答题
9.求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0交点的圆的方程.
[解] 法一:由
得到两圆公共弦为y=x,
由解得或
∴两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点分别为A(-1,-1),B(3,3),
线段AB的垂直平分线方程为y-1=-(x-1).
由得
∴所求圆的圆心为(3,-1),
半径为=4.
∴所求圆的方程为(x-3)2+(y+1)2=16.
法二:由法一知两圆交点为A(-1,-1),B(3,3).
设所求圆的方程为(x-a)2+(y-b)2=r2,
由得
∴所求圆的方程为(x-3)2+(y+1)2=16.
10.求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
[解] 设所求圆的圆心为P(a,b),则
=1. ①
(1)若两圆外切,
则有=1+2=3, ②
联立①②,解得a=5,b=-1,所以,所求圆的方程为(x-5)2+(y+1)2=1;
(2)若两圆内切,
则有=|2-1|=1, ③
联立①③,解得a=3,b=-1,所以,所求圆的方程为(x-3)2+(y+1)2=1.
综上所述,所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.
能力练
1.(多选题)已知圆C:(x-4)2+(y-3)2=4和两点A(0,-a),B(0,a)(a>0).若圆C上有且只有一点P,使得∠APB=90°,则a的值可能为( )
A.3 B.5 C.7 D.9
AC [根据题意,圆C:(x-4)2+(y-3)2=4,其圆心为(4,3),半径r=2;两点A(0,-a),B(0,a)(a>0),以AB为直径的圆的方程为x2+y2=a2,则该圆圆心为O(0,0),半径R=a.若点P满足∠APB=90°,则点P在圆x2+y2=a2上.
又由圆C上有且只有一点P,使得∠APB=90°,得圆C与圆x2+y2=a2相切,则有|OC|2=(0-4)2+(0-3)2=25=(2-a)2或|OC|2=(0-4)2+(0-3)2=25=(2+a)2,解得a=7或a=3.故选AC.]
2.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
A.4 B.4 C.8 D.8
C [∵两圆与两坐标轴都相切,且都经过点(4,1),∴两圆圆心均在第一象限且横、纵坐标相等.设两圆的圆心分别为(a,a),(b,b),则有(4-a)2+(1-a)2=a2,(4-b)2+(1-b)2=b2,即a,b为方程(4-x)2+(1-x)2=x2的两个根,
整理得x2-10x+17=0,
∴a+b=10,ab=17.
∴(a-b)2=(a+b)2-4ab=100-4×17=32,
∴|C1C2|===8.]
3.在直角坐标系xOy中,点A(x1,y1)和点B(x2,y2)是单位圆x2+y2=1上两点,|AB|=1,则∠AOB=_____________,|y1+2|+|y2+2|的最大值为________.
4+ [由|AB|=1,单位圆的半径为1,则△AOB为正三角形,故∠AOB=,设A(cos α,sin α),知B,则|y1+2|+|y2+2|=4+sin α+sin=4+sin,
故|y1+2|+|y2+2|的最大值为4+.]
4.与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是________.
(x-2)2+(y-2)2=2 [ 圆的方程化为(x-6)2+(y-6)2=18,其圆心C1(6,6)到直线x+y-2=0的距离为d==5.过点C1且垂直于x+y-2=0的直线为y-6=x-6,即y=x,所以所求的最小圆的圆心C2在直线y=x上,如图所示,
圆心C2到直线x+y-2=0的距离为=,则圆C2的半径长为.设圆心C2的坐标为(x0,y0),则=,y0=x0,解得x0=2(x0=0舍去),所以圆心坐标为(2,2),
所以所求圆的标准方程为(x-2)2+(y-2)2=2.]
拓展
在平面直角坐标系xOy中,已知圆M:(x-3)2+(y-4)2=4及其上一点A.
(1)求|OA|的最大值;
(2)设A(3,2),点T在x轴上.若圆M上存在两点P和Q,使得+=,求点T的横坐标的取值范围.
[解] (1)圆M:(x-3)2+(y-4)2=4的圆心为M(3,4),半径r=2.
根据平面几何知识得|OA|的最大值为|OM|+r=+2=7.
(2)设P(x1,y1),Q(x2,y2),T(t,0).
因为+=,所以(3-t,2)+(x1-t,y1)=(x2-t,y2),
即 ①
因为点Q在圆M上,所以(x2-3)2+(y2-4)2=4. ②
将①代入②,得(x1-t)2+(y1-2)2=4.
于是点P(x1,y1)既在圆M上,又在圆(x-t)2+(y-2)2=4上,
从而圆M:(x-3)2+(y-4)2=4与圆(x-t)2+(y-2)2=4有公共点.
所以2-2≤≤2+2,解得3-2≤t≤3+2,即点T的横坐标的取值范围为[3-2,3+2].
PAGE
(建议用时:40分钟)
基础练
一、选择题
1.圆x2+y2=4与圆x2+y2-2x+4y-4=0的位置关系为( )
A.相离 B.相交 C.相切 D.内含
2.圆x2+4x+y2=0与圆(x-2)2+(y-3)2=r2有三条公切线,则半径r=( )
A.5 B.4 C.3 D.2
3.若圆C:x2+(y-4)2=18与圆D:(x-1)2+(y-1)2=r2的公共弦长为6,则圆D的半径为( )
A.5 B.2 C.2 D.2
4.半径为5且与圆x2+y2-6x+8y=0相切于原点的圆的方程为( )
A.x2+y2-6x-8y=0
B.x2+y2+6x-8y=0
C.x2+y2+6x+8y=0
D.x2+y2-6x-8y=0或x2+y2-6x+8y=0
5.已知半径为1 cm的两圆外切,半径为2 cm且和这两圆都相切的圆共有( )
A.3个 B.4个 C.2个 D.5个
二、填空题
6.已知圆C的圆心为(2,1),若圆C与圆M:x2+y2-3x=0的公共弦所在直线过点(5,-2),则圆C的方程为________.
7.已知点P在圆x2+y2-8x-4y+11=0上,点Q在圆x2+y2+4x+2y+1=0上,则|PQ|的最小值是________.
8.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
三、解答题
9.求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0交点的圆的方程.
10.求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
能力练
1.(多选题)已知圆C:(x-4)2+(y-3)2=4和两点A(0,-a),B(0,a)(a>0).若圆C上有且只有一点P,使得∠APB=90°,则a的值可能为( )
A.3 B.5 C.7 D.9
2.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
A.4 B.4 C.8 D.8
3.在直角坐标系xOy中,点A(x1,y1)和点B(x2,y2)是单位圆x2+y2=1上两点,|AB|=1,则∠AOB=_____________,|y1+2|+|y2+2|的最大值为________.
4.与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是________.
拓展
在平面直角坐标系xOy中,已知圆M:(x-3)2+(y-4)2=4及其上一点A.
(1)求|OA|的最大值;
(2)设A(3,2),点T在x轴上.若圆M上存在两点P和Q,使得+=,求点T的横坐标的取值范围.
参考答案:
基础练
一、选择题
1.圆x2+y2=4与圆x2+y2-2x+4y-4=0的位置关系为( )
A.相离 B.相交 C.相切 D.内含
B [圆x2+y2=4的圆心坐标为(0,0),半径为2,圆x2+y2-2x+4y-4=0,即(x-1)2+(y+2)2=9,圆心坐标为(1,-2),半径为3,两圆的圆心距为=,半径和为5,半径差的绝对值为1,∵1<<5,∴两圆相交.]
2.圆x2+4x+y2=0与圆(x-2)2+(y-3)2=r2有三条公切线,则半径r=( )
A.5 B.4 C.3 D.2
C [两圆的圆心分别为(-2,0),(2,3),半径分别为2,r,由于两圆有三条公切线,所以两圆相外切,∴=2+r,即5=2+r,∴r=3.]
3.若圆C:x2+(y-4)2=18与圆D:(x-1)2+(y-1)2=r2的公共弦长为6,则圆D的半径为( )
A.5 B.2 C.2 D.2
D [两圆方程相减得2x-6y=4-r2,又由圆C的方程为x2+(y-4)2=18,其圆心为(0,4),半径r=3,两圆的公共弦长为6,则点(0,4)在直线2x-6y=4-r2上,则有2×0-6×4=4-r2,r2=28,r=2.]
4.半径为5且与圆x2+y2-6x+8y=0相切于原点的圆的方程为( )
A.x2+y2-6x-8y=0
B.x2+y2+6x-8y=0
C.x2+y2+6x+8y=0
D.x2+y2-6x-8y=0或x2+y2-6x+8y=0
B [已知圆的圆心为(3,-4),半径为5,所求圆的半径也为5,由两圆相切于原点,知所求圆的圆心与已知圆的圆心关于原点对称,即为(-3,4),可知选B.]
5.已知半径为1 cm的两圆外切,半径为2 cm且和这两圆都相切的圆共有( )
A.3个 B.4个 C.2个 D.5个
D [要全面分析所有的情况,包括都外切,都内切,一内切一外切.这样的圆共有5个,如图,它们是圆A、圆B、圆C、圆D、圆E.]
二、填空题
6.已知圆C的圆心为(2,1),若圆C与圆M:x2+y2-3x=0的公共弦所在直线过点(5,-2),则圆C的方程为________.
(x-2)2+(y-1)2=4 [设圆C的半径为r,则圆C的方程为(x-2)2+(y-1)2=r2,即x2+y2-4x-2y+5-r2=0.将圆C与圆M的方程相减得公共弦所在直线的方程为x+2y-5+r2=0.因为该直线过点(5,-2),所以r2=4.
故圆C的方程为(x-2)2+(y-1)2=4.]
7.已知点P在圆x2+y2-8x-4y+11=0上,点Q在圆x2+y2+4x+2y+1=0上,则|PQ|的最小值是________.
3-5 [两圆的圆心和半径分别为C1(4,2),r1=3,
C2(-2,-1),r2=2,|C1C2|=3,|C1C2|>r1+r2,∴两圆外离.
∴|PQ|min=|C1C2|-r1-r2=3-3-2=3-5.]
8.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
[圆C:(x-4)2+y2=1,如图,要满足直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,只需保证圆心C到y=kx-2的距离小于或等于2,
即≤2,解得0≤k≤.∴kmax=.]
三、解答题
9.求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0交点的圆的方程.
[解] 法一:由
得到两圆公共弦为y=x,
由解得或
∴两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点分别为A(-1,-1),B(3,3),
线段AB的垂直平分线方程为y-1=-(x-1).
由得
∴所求圆的圆心为(3,-1),
半径为=4.
∴所求圆的方程为(x-3)2+(y+1)2=16.
法二:由法一知两圆交点为A(-1,-1),B(3,3).
设所求圆的方程为(x-a)2+(y-b)2=r2,
由得
∴所求圆的方程为(x-3)2+(y+1)2=16.
10.求与圆(x-2)2+(y+1)2=4相切于点A(4,-1)且半径为1的圆的方程.
[解] 设所求圆的圆心为P(a,b),则
=1. ①
(1)若两圆外切,
则有=1+2=3, ②
联立①②,解得a=5,b=-1,所以,所求圆的方程为(x-5)2+(y+1)2=1;
(2)若两圆内切,
则有=|2-1|=1, ③
联立①③,解得a=3,b=-1,所以,所求圆的方程为(x-3)2+(y+1)2=1.
综上所述,所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.
能力练
1.(多选题)已知圆C:(x-4)2+(y-3)2=4和两点A(0,-a),B(0,a)(a>0).若圆C上有且只有一点P,使得∠APB=90°,则a的值可能为( )
A.3 B.5 C.7 D.9
AC [根据题意,圆C:(x-4)2+(y-3)2=4,其圆心为(4,3),半径r=2;两点A(0,-a),B(0,a)(a>0),以AB为直径的圆的方程为x2+y2=a2,则该圆圆心为O(0,0),半径R=a.若点P满足∠APB=90°,则点P在圆x2+y2=a2上.
又由圆C上有且只有一点P,使得∠APB=90°,得圆C与圆x2+y2=a2相切,则有|OC|2=(0-4)2+(0-3)2=25=(2-a)2或|OC|2=(0-4)2+(0-3)2=25=(2+a)2,解得a=7或a=3.故选AC.]
2.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )
A.4 B.4 C.8 D.8
C [∵两圆与两坐标轴都相切,且都经过点(4,1),∴两圆圆心均在第一象限且横、纵坐标相等.设两圆的圆心分别为(a,a),(b,b),则有(4-a)2+(1-a)2=a2,(4-b)2+(1-b)2=b2,即a,b为方程(4-x)2+(1-x)2=x2的两个根,
整理得x2-10x+17=0,
∴a+b=10,ab=17.
∴(a-b)2=(a+b)2-4ab=100-4×17=32,
∴|C1C2|===8.]
3.在直角坐标系xOy中,点A(x1,y1)和点B(x2,y2)是单位圆x2+y2=1上两点,|AB|=1,则∠AOB=_____________,|y1+2|+|y2+2|的最大值为________.
4+ [由|AB|=1,单位圆的半径为1,则△AOB为正三角形,故∠AOB=,设A(cos α,sin α),知B,则|y1+2|+|y2+2|=4+sin α+sin=4+sin,
故|y1+2|+|y2+2|的最大值为4+.]
4.与直线x+y-2=0和圆x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是________.
(x-2)2+(y-2)2=2 [ 圆的方程化为(x-6)2+(y-6)2=18,其圆心C1(6,6)到直线x+y-2=0的距离为d==5.过点C1且垂直于x+y-2=0的直线为y-6=x-6,即y=x,所以所求的最小圆的圆心C2在直线y=x上,如图所示,
圆心C2到直线x+y-2=0的距离为=,则圆C2的半径长为.设圆心C2的坐标为(x0,y0),则=,y0=x0,解得x0=2(x0=0舍去),所以圆心坐标为(2,2),
所以所求圆的标准方程为(x-2)2+(y-2)2=2.]
拓展
在平面直角坐标系xOy中,已知圆M:(x-3)2+(y-4)2=4及其上一点A.
(1)求|OA|的最大值;
(2)设A(3,2),点T在x轴上.若圆M上存在两点P和Q,使得+=,求点T的横坐标的取值范围.
[解] (1)圆M:(x-3)2+(y-4)2=4的圆心为M(3,4),半径r=2.
根据平面几何知识得|OA|的最大值为|OM|+r=+2=7.
(2)设P(x1,y1),Q(x2,y2),T(t,0).
因为+=,所以(3-t,2)+(x1-t,y1)=(x2-t,y2),
即 ①
因为点Q在圆M上,所以(x2-3)2+(y2-4)2=4. ②
将①代入②,得(x1-t)2+(y1-2)2=4.
于是点P(x1,y1)既在圆M上,又在圆(x-t)2+(y-2)2=4上,
从而圆M:(x-3)2+(y-4)2=4与圆(x-t)2+(y-2)2=4有公共点.
所以2-2≤≤2+2,解得3-2≤t≤3+2,即点T的横坐标的取值范围为[3-2,3+2].
PAGE
