2021-2022学年北师大版九年级数学上册4.1成比例线段第2课时比例的性质课件(19张)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.1成比例线段第2课时比例的性质课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 08:14:42 | ||
图片预览






文档简介
(共19张PPT)
第四章图形的相似
4.1 第2课时
比例的性质
目 录
CONTENTS
01 比的基本性质
02 合分比性质
03 等比性质
04 随堂练习
01
比的基本性质
01
比的基本性质——复习回顾
复习回顾:
(1)如果a与b的比值和c与d的比值相等,应记为:____________。
(2)已知2:3=4:x,则x=_________。
(3)线段的比是指_______条线段的比的关系,成比例线段是指_____条线段之间的关系。
注意:概念的有序性
线段的比有顺序性,a:b和b:a相等吗?请举例说明。
成比例线段也有顺序性,如 能说成是b、a、c、d成比例吗?请举例说明。
6
2
4
01
比的基本性质
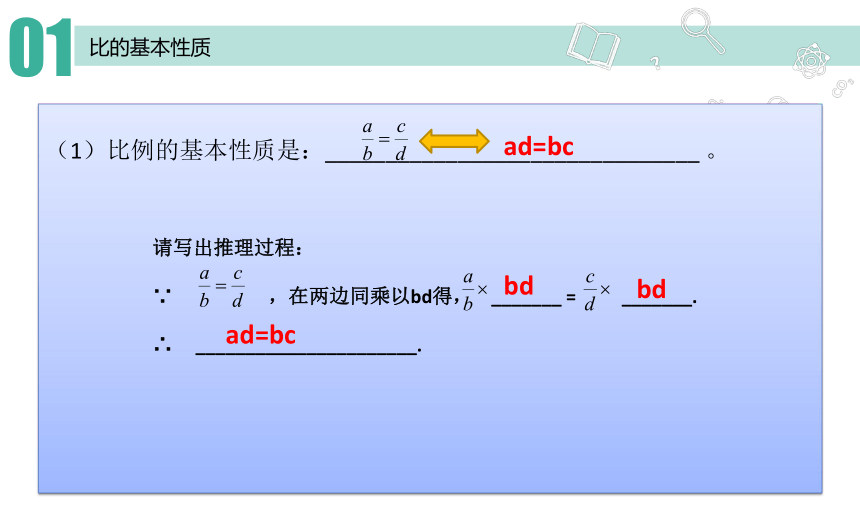
(1)比例的基本性质是:_______________________________ 。
ad=bc
请写出推理过程:
∵ ,在两边同乘以bd得, _______ = _______.
∴ ______________________.
bd
ad=bc
bd
01
比的基本性质
例1.已知 ,求 的值.
解法1:由比例的基本性质,得2(a+3b)=7×2b.∴a=4b,∴ =4.
解法2:由 ,
得 =7,
∴ + = +3=7,∴=4.
01
比的基本性质
练习:
若 x : 2 = (x-4) : 4 ,则x=__________。
解:∵ x : 2 = (x-4) : 4
∴由比的基本性质可知 4x = 2(x-4)
解得 x=-4
-4
02
合比性质,等比性质
02
合分比性质
(2)合比性质:如果 ,那么 ______________.
请写出推理过程:
∵ ,在两边同时加上1得, + ____ = + _____ .
两边分别通分得:
思考:请仿照上面的方法,证明
“如果 ,则 。”
1
1
分比性质
02
合分比性质
例2.已知: ,求证
证明:∵
∴ (合分比性质)
∴
∴
∴
02
4k
合分比性质
练习:已知a:b:c=2:4:5,且2a-b+3c=6,求3a+2b+4c的值。
解:设a=2k,b=4k,c=5k
则 ∵2a-b+3c=6
∴ 4k-4k+15k=6
解得 k=0.4
∴ 3a+2b+4c=6k+8k+20k=34k=13.6
03
等比性质
03
等比性质
等比性质:如果 (b+d+...+n≠0 ),那么 .
思考:等比性质中,为什么要 b+d+...+n≠0 这个条件?
03
等比性质
例3.(1)已知a:b:c=3:4:5,求 的值;
(2)已知 =2,且b+d+f≠0,求 的值.
解:(1)设a:b:c=3:4:5=k,则a=3k,b=4k,c=5k,
∴ = =
(2)∵ =2,∴ =2
∴ =2
03
等比性质
例4.若a,b,c都是不等于零的数,且 ,求k的值。
解:当a+b+c≠0时,由 得
即 ,即 k=2
当a+b+c=0时,则有a+b=-c.
此时 .
综上所述,k的值是2或-1.
03
等比性质
练习:(1)已知 ,求x的值;
(2)已知 ,求 的值
04
随堂练习
04
随堂练习
1.在相同时刻的物高与影长成比例,如果一建筑在地面上影长为50米,高为1.5米的测竿的影长为2.5米,那么,该建筑的高是多少米?
2.已知:x∶y∶z=2∶3∶4求:⑴ ; ⑵ ;⑶
3.已知实数a,b,c满足 ,求 的值.
THANK YOU!
谢谢欣赏
第四章图形的相似
4.1 第2课时
比例的性质
目 录
CONTENTS
01 比的基本性质
02 合分比性质
03 等比性质
04 随堂练习
01
比的基本性质
01
比的基本性质——复习回顾
复习回顾:
(1)如果a与b的比值和c与d的比值相等,应记为:____________。
(2)已知2:3=4:x,则x=_________。
(3)线段的比是指_______条线段的比的关系,成比例线段是指_____条线段之间的关系。
注意:概念的有序性
线段的比有顺序性,a:b和b:a相等吗?请举例说明。
成比例线段也有顺序性,如 能说成是b、a、c、d成比例吗?请举例说明。
6
2
4
01
比的基本性质
(1)比例的基本性质是:_______________________________ 。
ad=bc
请写出推理过程:
∵ ,在两边同乘以bd得, _______ = _______.
∴ ______________________.
bd
ad=bc
bd
01
比的基本性质
例1.已知 ,求 的值.
解法1:由比例的基本性质,得2(a+3b)=7×2b.∴a=4b,∴ =4.
解法2:由 ,
得 =7,
∴ + = +3=7,∴=4.
01
比的基本性质
练习:
若 x : 2 = (x-4) : 4 ,则x=__________。
解:∵ x : 2 = (x-4) : 4
∴由比的基本性质可知 4x = 2(x-4)
解得 x=-4
-4
02
合比性质,等比性质
02
合分比性质
(2)合比性质:如果 ,那么 ______________.
请写出推理过程:
∵ ,在两边同时加上1得, + ____ = + _____ .
两边分别通分得:
思考:请仿照上面的方法,证明
“如果 ,则 。”
1
1
分比性质
02
合分比性质
例2.已知: ,求证
证明:∵
∴ (合分比性质)
∴
∴
∴
02
4k
合分比性质
练习:已知a:b:c=2:4:5,且2a-b+3c=6,求3a+2b+4c的值。
解:设a=2k,b=4k,c=5k
则 ∵2a-b+3c=6
∴ 4k-4k+15k=6
解得 k=0.4
∴ 3a+2b+4c=6k+8k+20k=34k=13.6
03
等比性质
03
等比性质
等比性质:如果 (b+d+...+n≠0 ),那么 .
思考:等比性质中,为什么要 b+d+...+n≠0 这个条件?
03
等比性质
例3.(1)已知a:b:c=3:4:5,求 的值;
(2)已知 =2,且b+d+f≠0,求 的值.
解:(1)设a:b:c=3:4:5=k,则a=3k,b=4k,c=5k,
∴ = =
(2)∵ =2,∴ =2
∴ =2
03
等比性质
例4.若a,b,c都是不等于零的数,且 ,求k的值。
解:当a+b+c≠0时,由 得
即 ,即 k=2
当a+b+c=0时,则有a+b=-c.
此时 .
综上所述,k的值是2或-1.
03
等比性质
练习:(1)已知 ,求x的值;
(2)已知 ,求 的值
04
随堂练习
04
随堂练习
1.在相同时刻的物高与影长成比例,如果一建筑在地面上影长为50米,高为1.5米的测竿的影长为2.5米,那么,该建筑的高是多少米?
2.已知:x∶y∶z=2∶3∶4求:⑴ ; ⑵ ;⑶
3.已知实数a,b,c满足 ,求 的值.
THANK YOU!
谢谢欣赏
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
