沪教版2022届高考数学一轮复习讲义专题18:空间直线与平面复习与检测(Word含答案解析)
文档属性
| 名称 | 沪教版2022届高考数学一轮复习讲义专题18:空间直线与平面复习与检测(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 713.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 20:40:55 | ||
图片预览




文档简介
学习目标
1.掌握画空间图形的基本技能,培养空间想象能力,
2.理解异面直线所成角的概念,
3.会画简单图形中的异面直线所成角的大小。
知识梳理
重点1
直线的对称式(点向式)方程
空间给定了一点与一个非零向量,那么通过点且与向量平行的直线就被唯一确定,向量叫直线的方向向量.
任何一个与直线平行的非零向量都可以作为直线的方向向量.
重点2
直线一般方程与标准方程的互化
标准方程化为一般方程.(方向数不全为零)
一般方程化为标准方程
一般方程
确定直线的两平面法向量的向量积为直线的一个方向 向量.
(2)取方程组的一组特解得直线上一点化得直线标准方程:
重点3
空间平面的一般方程
一个平面I是由垂直它的非零向量n和平面上的一个点M唯一决定的。设n=(A,B,C)(不为零向量)表示垂直I的方向,称n为I的法向量
由于n为平面I的法向量,M0(x0,y0,z0)为I上一点,则对于空间中任意一点M(x,y,z),M在I上当且仅当
或 (3.1.2—1)
用坐标来表示,化为
令,则得到平面的方程
(3.1.2—2)
这样,任何一张平面都可以用一个三元一次方程来表示。反之,对于任何一个三元一次方程
不全为0,
不妨设,则该方程又可写成
作过点,垂直于方向的平面,则这个平面的方程就是所给出的方程,即一个三元一次方程表示一个平面。由此可以看出,经由坐标系,空间中的平面与一个四元数组相对应。但是,这种对应不是一对一的,对于所有的,对应同一平面。由(3.1.2—2)表示的方程称为平面的一般方程。
重点4
空间中直线与平面的位置关系
已知直线和平面的方程为
现在我们来讨论,,在上的充要条件。
因为直线的方向向量与直线平行,平面的法向量与平面垂直,所以有
如果时,和又有公共点,则就整个落在上了.因此有
在上
空间直线与平面的交角
设直线和平面的交角为.当时,;当时,;其他情况下,等于与它在上的射影直线所交的锐角.
设是的方向向量与的法向量之间的夹角,则有
或
或
因此在这两种情况下,都有.
已知直线和平面的方程为
设和的交角为,则
例题分析
例1.如图,矩形中,已知为的中点.将沿着向上翻折至得到四棱锥.平面与平面所成锐二面角为,直线与平面所成角为,则下列说法错误的是( )
A.若为中点,则无论翻折到哪个位置都有平面平面
B.若为中点,则无论翻折到哪个位置都有平面
C.
D.存在某一翻折位置,使
【答案】C
【详解】
若为中点,连接交于点,则面,又面,所以平面平面,故A正确;
取中点,则,,又,
所以四边形PECQ是平行四边形,又平面,平面,所以平面,故B正确;
过作平面,则在上,所以平面与平面所成锐二面角为(或其补角),
,故C错误;
若,又,则,故D正确,
故选:C.
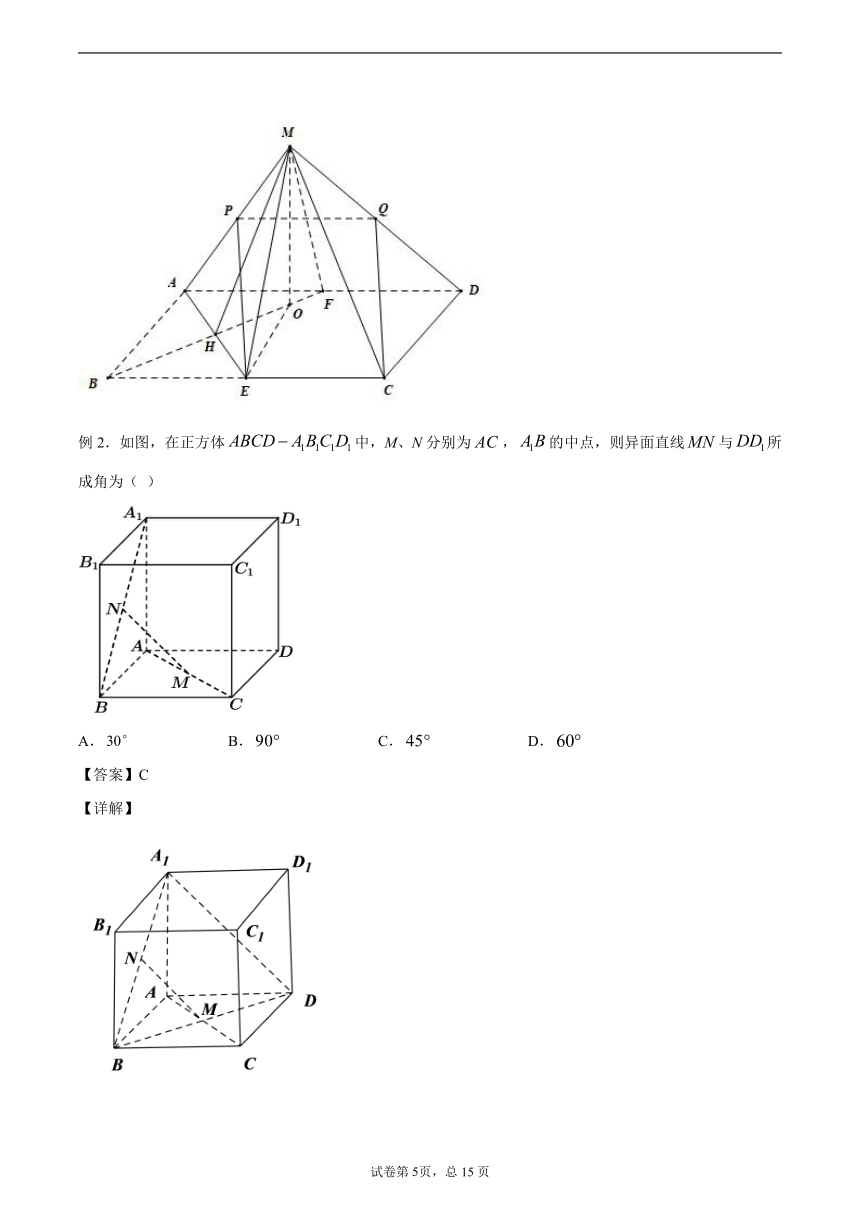
例2.如图,在正方体中,M、N分别为,的中点,则异面直线与所成角为( )
A. B. C. D.
【答案】C
【详解】
如图,在正方体中,连接交于,
连接,M、N分别为,的中点,所以,
所以异面直线与所成角即与所成角,
易知,
故选:C.
跟踪练习
1.已知直线l平行于平面,平面垂直于平面,则以下关于直线l与平面β的位置关系的表述,正确的是( )
A.l与垂直 B.l与无公共点
C.l与至少有一个公共点 D.在内,l与平行,l与相交都有可能
2.设正四棱柱的底面边长为1,高为2,平面经过顶点,且与棱所在直线所成的角都相等,则满足条件的平面共有( )个.
A.1 B.2 C.3 D.4
3.如图,面,为矩形,连接 ,下面各组向量中,数量积不一定为零的是( )
A.与 B.与
C.与 D.与
4.下列命题为真命题的是( )
A.若直线l与平面α上的两条直线垂直,则直线l与平面α垂直
B.若两条直线同时垂直于一个平面,则这两条直线平行
C.若两个平面同时垂直于第三个平面,则这两个平面垂直
D.若直线l上的不同两点到平面α的距离相等,则直线l与平面α平行
5.设直线l与平面平行,直线m在平面上,那么( )
A.直线l平行于直线m B.直线l与直线m异面
C.直线l与直线m没有公共点 D.直线l与直线m不垂直
6.已知空间直线和平面,则“直线在平面外”是“直线∥平面”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
7.如图,已知四棱锥中,底面是边长为2的正方形,,,M是的中点.
(1)证明:;
(2)求点B到平面的距离.
8.已知如图①,在菱形中,且为的中点,将沿折起使,得到如图②所示的四棱锥,在四棱锥中求解下列问题:
(1)求证:平面;
(2)若为的中点,求直线与平面所成的角.
9.如图,已知正三棱柱的体积为,底面边长为3,求异面直线与所成的角的大小.
10.如图,在几何体中,已知平面,且四边形为直角梯形,,,.
(1)求证:平面;
(2)若PC与平面所成的角为,求点A到平面的距离.试卷第1页,总3页
试卷第15页,总15页
参考答案
1.D
【详解】
因平面垂直于平面,令,当时满足条件,从而选项A,B都不正确;
过直线a作平面,与平面,平面都不重合,直线l在内与a平行时满足条件,此时,即C选项不正确;
在平面内作一直线b与直线a相交,直线l与b平行时满足条件,此时l与相交,选项D正确.
故选:D
2.D
【详解】
解:第一类:
①在平面的一边在另一边,有一个平面符合条件;
②在平面的一边在另一边,有一个平面符合条件;
③在平面的一边在另一边,有一个平面符合条件;
第二类:
都在平面的同侧,有一个平面符合条件.
综上所述,满足条件的平面共有4个.
故选:D.
3.A
【详解】
由面,为矩形,
A:面,则,而与不一定垂直,不一定有面,故不一定与垂直,所以与数量积不一定为0,符合题意;
B:由A知,又且,则面,又面,所以,即与数量积为0,不合题意;
C:由上易知,又 且,则面,又面,所以,即与数量积为0,不合题意;
D:由上知,而,所以,即与数量积为0,不合题意;
故选:A.
4.B
【详解】
A. 若直线l与平面α上的两条直线垂直,当平面内两条直线平行时,直线l与平面α不一定垂直,A错;
B. 若两条直线同时垂直于一个平面,则这两条直线平行,这是线面垂直的性质定理,B正确;
C. 若两个平面同时垂直于第三个平面,则这两个平面垂直,这两个平面可以相交,也可以平行,C错;
D. 若直线l上的不同两点到平面α的距离相等,直线l与平面α可能相交也可能平行,D错.
故选:B.
5.C
【详解】
若直线l与平面平行,直线m在平面上,
则直线l平行于直线m或直线l与直线m异面,所以直线l与直线m没有公共点
故选:C
6.B
【详解】
直线在平面外,包括直线与平面平行和相交,不充分,但直线∥平面,一定有直线在平面外,必要的,因此是必要不充分条件.
故选:B.
7.(1)证明见解析;(2).
【详解】
(1)底面是边长为2的正方形,,M是的中点,
∴,
∵∴平面
∴,,
∴平面,∴.
(2)∵平面∴,
过于点,,
,
(设B到面的距离为h),
∴.
8.(1)证明见解析;(2).
【详解】
(1)在图①中,连接,如图所示.
因为四边形为菱形,,所以是等边三角形.
因为为的中点,所以
又,所以.
在图②中,,所以,即.
因为所以
又均在平面内,所以平面
(2)由(1)知,
因为在平面内,所以平面
以为坐标原点,的方向分别为轴,轴,轴,建立如图所示的空间直角坐标系,
则
设平面的一个法向量为.
因为,
由得
令,得,又
设直线与平面所成的角为,则.
故,
所以直线与平面所成的角为.
9.异面直线与与所成的角的大小为
【详解】
设正三棱柱的高为h,则,
由,得.
因为,所以与所成的角等于与所成的角.
连接,在中,
,
由,
得
故异面直线与与所成的角的大小为.
10.(1)证明见解析;(2)点A到平面PCD的距离为.
【详解】
(1)连接AC,∵AB=BC=1,∠ABC为直角,∴AC=,∠BAC=,
又∵∠BAD=,∴∠CAD=,
又∵AD=2,
∴ACD为等腰直角三角形,∴AC⊥BC,
又∵PA⊥底面ABCD,∴PA⊥CD,
又∵PA∩AC=A,PA,AC 平面PAC,
∴CD⊥平面PAC;
(2)∵PA⊥平面ABCD,∴∠PCA是PC与平面ABCD所成的角,
故由已知得∠PCA=,
在PAC中,过A作AH⊥PC,垂足为H,
则A到斜边PC的距离AH=ACsin,
∵CD⊥平面PAC,CD 平面PCD,∴平面PAC⊥平面PCD,
又∵平面PAC∩平面PCD=PC,
AH⊥PC,AH 平面PAC,
∴AH⊥平面PCD,
即AH就是A到平面PCD的距离,
∴A到平面PCD的距离为.
1.掌握画空间图形的基本技能,培养空间想象能力,
2.理解异面直线所成角的概念,
3.会画简单图形中的异面直线所成角的大小。
知识梳理
重点1
直线的对称式(点向式)方程
空间给定了一点与一个非零向量,那么通过点且与向量平行的直线就被唯一确定,向量叫直线的方向向量.
任何一个与直线平行的非零向量都可以作为直线的方向向量.
重点2
直线一般方程与标准方程的互化
标准方程化为一般方程.(方向数不全为零)
一般方程化为标准方程
一般方程
确定直线的两平面法向量的向量积为直线的一个方向 向量.
(2)取方程组的一组特解得直线上一点化得直线标准方程:
重点3
空间平面的一般方程
一个平面I是由垂直它的非零向量n和平面上的一个点M唯一决定的。设n=(A,B,C)(不为零向量)表示垂直I的方向,称n为I的法向量
由于n为平面I的法向量,M0(x0,y0,z0)为I上一点,则对于空间中任意一点M(x,y,z),M在I上当且仅当
或 (3.1.2—1)
用坐标来表示,化为
令,则得到平面的方程
(3.1.2—2)
这样,任何一张平面都可以用一个三元一次方程来表示。反之,对于任何一个三元一次方程
不全为0,
不妨设,则该方程又可写成
作过点,垂直于方向的平面,则这个平面的方程就是所给出的方程,即一个三元一次方程表示一个平面。由此可以看出,经由坐标系,空间中的平面与一个四元数组相对应。但是,这种对应不是一对一的,对于所有的,对应同一平面。由(3.1.2—2)表示的方程称为平面的一般方程。
重点4
空间中直线与平面的位置关系
已知直线和平面的方程为
现在我们来讨论,,在上的充要条件。
因为直线的方向向量与直线平行,平面的法向量与平面垂直,所以有
如果时,和又有公共点,则就整个落在上了.因此有
在上
空间直线与平面的交角
设直线和平面的交角为.当时,;当时,;其他情况下,等于与它在上的射影直线所交的锐角.
设是的方向向量与的法向量之间的夹角,则有
或
或
因此在这两种情况下,都有.
已知直线和平面的方程为
设和的交角为,则
例题分析
例1.如图,矩形中,已知为的中点.将沿着向上翻折至得到四棱锥.平面与平面所成锐二面角为,直线与平面所成角为,则下列说法错误的是( )
A.若为中点,则无论翻折到哪个位置都有平面平面
B.若为中点,则无论翻折到哪个位置都有平面
C.
D.存在某一翻折位置,使
【答案】C
【详解】
若为中点,连接交于点,则面,又面,所以平面平面,故A正确;
取中点,则,,又,
所以四边形PECQ是平行四边形,又平面,平面,所以平面,故B正确;
过作平面,则在上,所以平面与平面所成锐二面角为(或其补角),
,故C错误;
若,又,则,故D正确,
故选:C.
例2.如图,在正方体中,M、N分别为,的中点,则异面直线与所成角为( )
A. B. C. D.
【答案】C
【详解】
如图,在正方体中,连接交于,
连接,M、N分别为,的中点,所以,
所以异面直线与所成角即与所成角,
易知,
故选:C.
跟踪练习
1.已知直线l平行于平面,平面垂直于平面,则以下关于直线l与平面β的位置关系的表述,正确的是( )
A.l与垂直 B.l与无公共点
C.l与至少有一个公共点 D.在内,l与平行,l与相交都有可能
2.设正四棱柱的底面边长为1,高为2,平面经过顶点,且与棱所在直线所成的角都相等,则满足条件的平面共有( )个.
A.1 B.2 C.3 D.4
3.如图,面,为矩形,连接 ,下面各组向量中,数量积不一定为零的是( )
A.与 B.与
C.与 D.与
4.下列命题为真命题的是( )
A.若直线l与平面α上的两条直线垂直,则直线l与平面α垂直
B.若两条直线同时垂直于一个平面,则这两条直线平行
C.若两个平面同时垂直于第三个平面,则这两个平面垂直
D.若直线l上的不同两点到平面α的距离相等,则直线l与平面α平行
5.设直线l与平面平行,直线m在平面上,那么( )
A.直线l平行于直线m B.直线l与直线m异面
C.直线l与直线m没有公共点 D.直线l与直线m不垂直
6.已知空间直线和平面,则“直线在平面外”是“直线∥平面”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
7.如图,已知四棱锥中,底面是边长为2的正方形,,,M是的中点.
(1)证明:;
(2)求点B到平面的距离.
8.已知如图①,在菱形中,且为的中点,将沿折起使,得到如图②所示的四棱锥,在四棱锥中求解下列问题:
(1)求证:平面;
(2)若为的中点,求直线与平面所成的角.
9.如图,已知正三棱柱的体积为,底面边长为3,求异面直线与所成的角的大小.
10.如图,在几何体中,已知平面,且四边形为直角梯形,,,.
(1)求证:平面;
(2)若PC与平面所成的角为,求点A到平面的距离.试卷第1页,总3页
试卷第15页,总15页
参考答案
1.D
【详解】
因平面垂直于平面,令,当时满足条件,从而选项A,B都不正确;
过直线a作平面,与平面,平面都不重合,直线l在内与a平行时满足条件,此时,即C选项不正确;
在平面内作一直线b与直线a相交,直线l与b平行时满足条件,此时l与相交,选项D正确.
故选:D
2.D
【详解】
解:第一类:
①在平面的一边在另一边,有一个平面符合条件;
②在平面的一边在另一边,有一个平面符合条件;
③在平面的一边在另一边,有一个平面符合条件;
第二类:
都在平面的同侧,有一个平面符合条件.
综上所述,满足条件的平面共有4个.
故选:D.
3.A
【详解】
由面,为矩形,
A:面,则,而与不一定垂直,不一定有面,故不一定与垂直,所以与数量积不一定为0,符合题意;
B:由A知,又且,则面,又面,所以,即与数量积为0,不合题意;
C:由上易知,又 且,则面,又面,所以,即与数量积为0,不合题意;
D:由上知,而,所以,即与数量积为0,不合题意;
故选:A.
4.B
【详解】
A. 若直线l与平面α上的两条直线垂直,当平面内两条直线平行时,直线l与平面α不一定垂直,A错;
B. 若两条直线同时垂直于一个平面,则这两条直线平行,这是线面垂直的性质定理,B正确;
C. 若两个平面同时垂直于第三个平面,则这两个平面垂直,这两个平面可以相交,也可以平行,C错;
D. 若直线l上的不同两点到平面α的距离相等,直线l与平面α可能相交也可能平行,D错.
故选:B.
5.C
【详解】
若直线l与平面平行,直线m在平面上,
则直线l平行于直线m或直线l与直线m异面,所以直线l与直线m没有公共点
故选:C
6.B
【详解】
直线在平面外,包括直线与平面平行和相交,不充分,但直线∥平面,一定有直线在平面外,必要的,因此是必要不充分条件.
故选:B.
7.(1)证明见解析;(2).
【详解】
(1)底面是边长为2的正方形,,M是的中点,
∴,
∵∴平面
∴,,
∴平面,∴.
(2)∵平面∴,
过于点,,
,
(设B到面的距离为h),
∴.
8.(1)证明见解析;(2).
【详解】
(1)在图①中,连接,如图所示.
因为四边形为菱形,,所以是等边三角形.
因为为的中点,所以
又,所以.
在图②中,,所以,即.
因为所以
又均在平面内,所以平面
(2)由(1)知,
因为在平面内,所以平面
以为坐标原点,的方向分别为轴,轴,轴,建立如图所示的空间直角坐标系,
则
设平面的一个法向量为.
因为,
由得
令,得,又
设直线与平面所成的角为,则.
故,
所以直线与平面所成的角为.
9.异面直线与与所成的角的大小为
【详解】
设正三棱柱的高为h,则,
由,得.
因为,所以与所成的角等于与所成的角.
连接,在中,
,
由,
得
故异面直线与与所成的角的大小为.
10.(1)证明见解析;(2)点A到平面PCD的距离为.
【详解】
(1)连接AC,∵AB=BC=1,∠ABC为直角,∴AC=,∠BAC=,
又∵∠BAD=,∴∠CAD=,
又∵AD=2,
∴ACD为等腰直角三角形,∴AC⊥BC,
又∵PA⊥底面ABCD,∴PA⊥CD,
又∵PA∩AC=A,PA,AC 平面PAC,
∴CD⊥平面PAC;
(2)∵PA⊥平面ABCD,∴∠PCA是PC与平面ABCD所成的角,
故由已知得∠PCA=,
在PAC中,过A作AH⊥PC,垂足为H,
则A到斜边PC的距离AH=ACsin,
∵CD⊥平面PAC,CD 平面PCD,∴平面PAC⊥平面PCD,
又∵平面PAC∩平面PCD=PC,
AH⊥PC,AH 平面PAC,
∴AH⊥平面PCD,
即AH就是A到平面PCD的距离,
∴A到平面PCD的距离为.
同课章节目录
