2021_2022学年新教材高中数学1.2.3直线与平面的夹角(Word含答案解析)
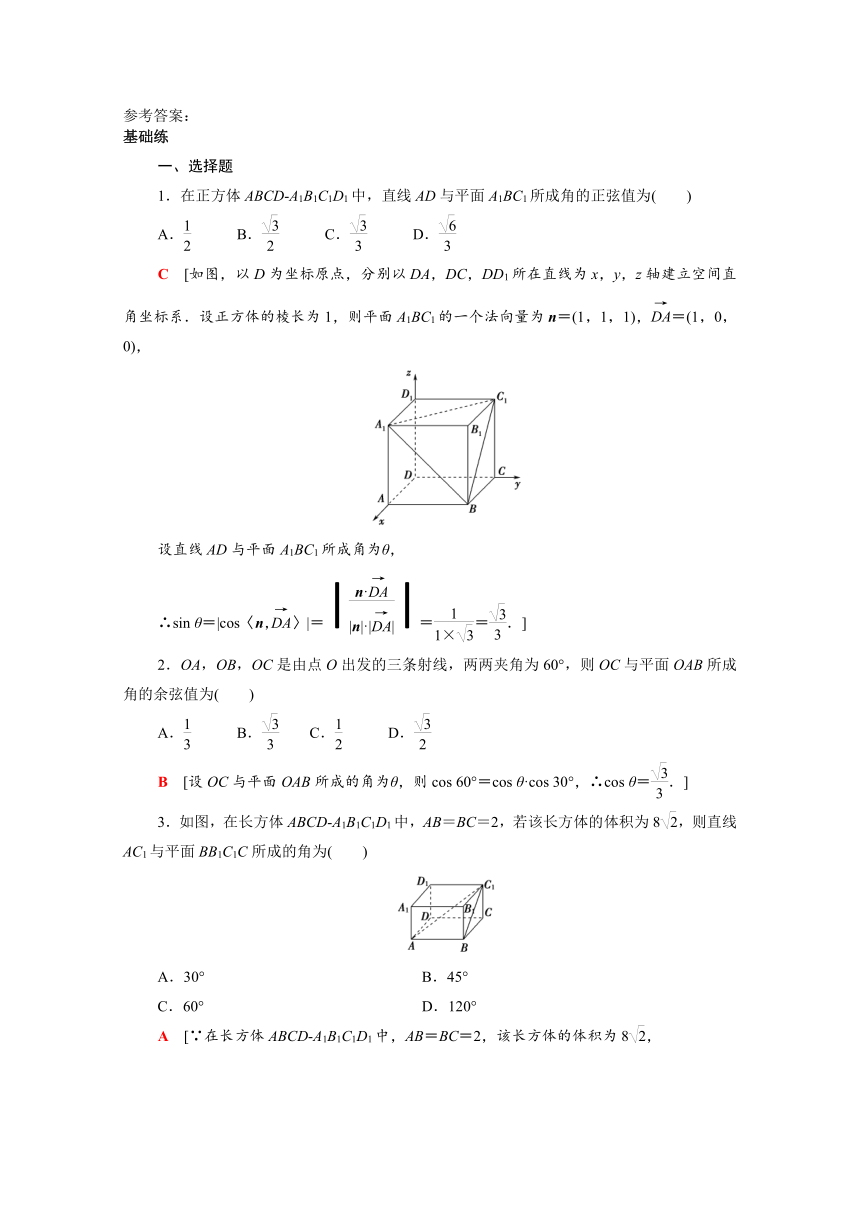
文档属性
| 名称 | 2021_2022学年新教材高中数学1.2.3直线与平面的夹角(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 607.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 20:45:03 | ||
图片预览


文档简介
直线与平面的夹角
(建议用时:40分钟)
基础练
一、选择题
1.在正方体ABCD A1B1C1D1中,直线AD与平面A1BC1所成角的正弦值为( )
A. B. C. D.
2.OA,OB,OC是由点O出发的三条射线,两两夹角为60°,则OC与平面OAB所成角的余弦值为( )
A. B. C. D.
3.如图,在长方体ABCD A1B1C1D1中,AB=BC=2,若该长方体的体积为8,则直线AC1与平面BB1C1C所成的角为( )
A.30° B.45°
C.60° D.120°
4.如图,长方体ABCD A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成角的正弦值为( )
A. B. C. D.
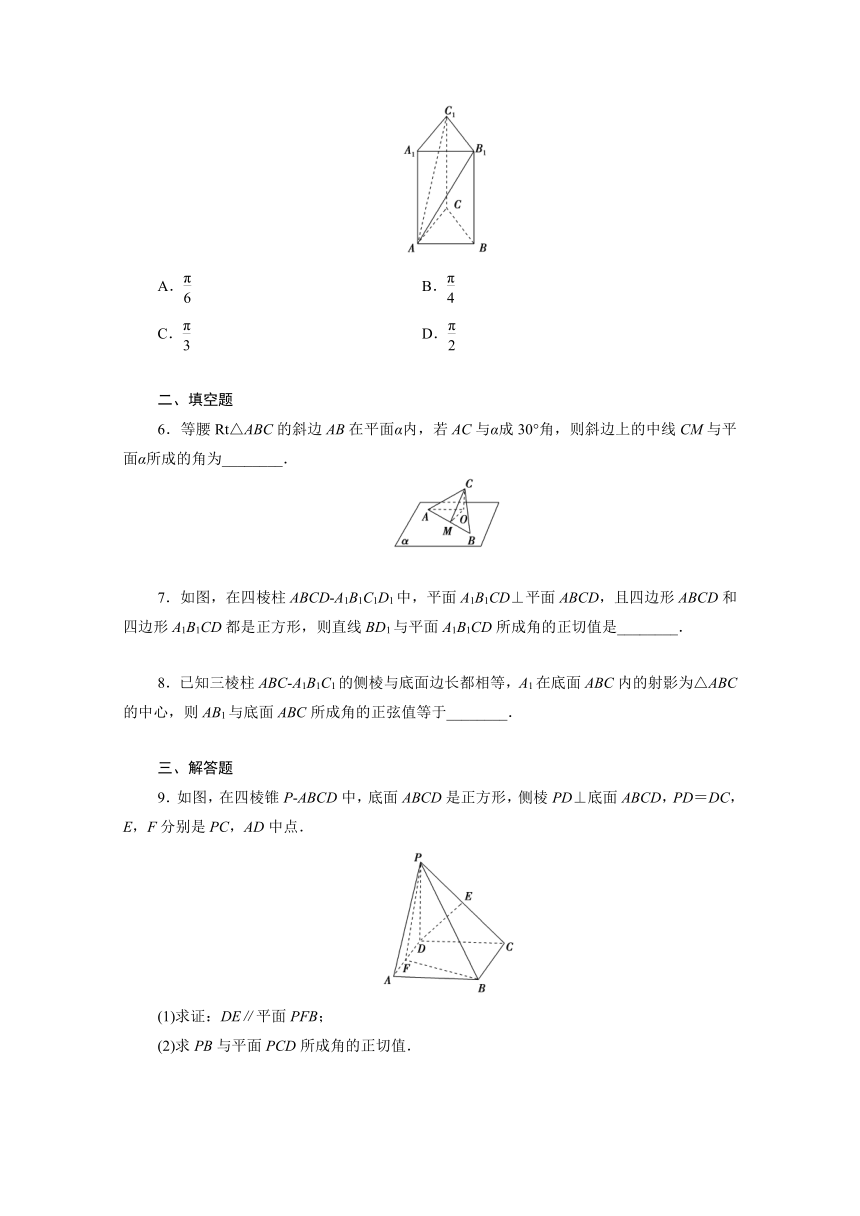
5.如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则AA1与平面AB1C1所成的角为( )
A. B.
C. D.
二、填空题
6.等腰Rt△ABC的斜边AB在平面α内,若AC与α成30°角,则斜边上的中线CM与平面α所成的角为________.
7.如图,在四棱柱ABCD A1B1C1D1中,平面A1B1CD⊥平面ABCD,且四边形ABCD和四边形A1B1CD都是正方形,则直线BD1与平面A1B1CD所成角的正切值是________.
8.已知三棱柱ABC A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于________.
三、解答题
9.如图,在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E,F分别是PC,AD中点.
(1)求证:DE∥平面PFB;
(2)求PB与平面PCD所成角的正切值.
10.在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,EC=2,F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求直线AD与平面BCE所成角的正弦值.
能力练
1.(多选题)已知四棱锥P ABCD的四条侧棱都相等,底面是边长为2的正方形,若其五个顶点都在一个表面积为的球面上,则PA与底面ABCD所成角的正弦值为( )
A. B. C. D.
2.在圆柱OO1中,O是上底面圆心,AB是下底面圆的直径,点C在下底面圆周上,若△OAB是正三角形,O1C⊥AB,则OC与平面OAB所成角为( )
A.150° B.30° C.45° D.60°
3.在正方体ABCD A1B1C1D1中,E,F分别为AB,BC的中点,则直线CD1与C1F所成角的余弦值为________,直线CD1与平面A1C1FE所成角的正弦值为________.
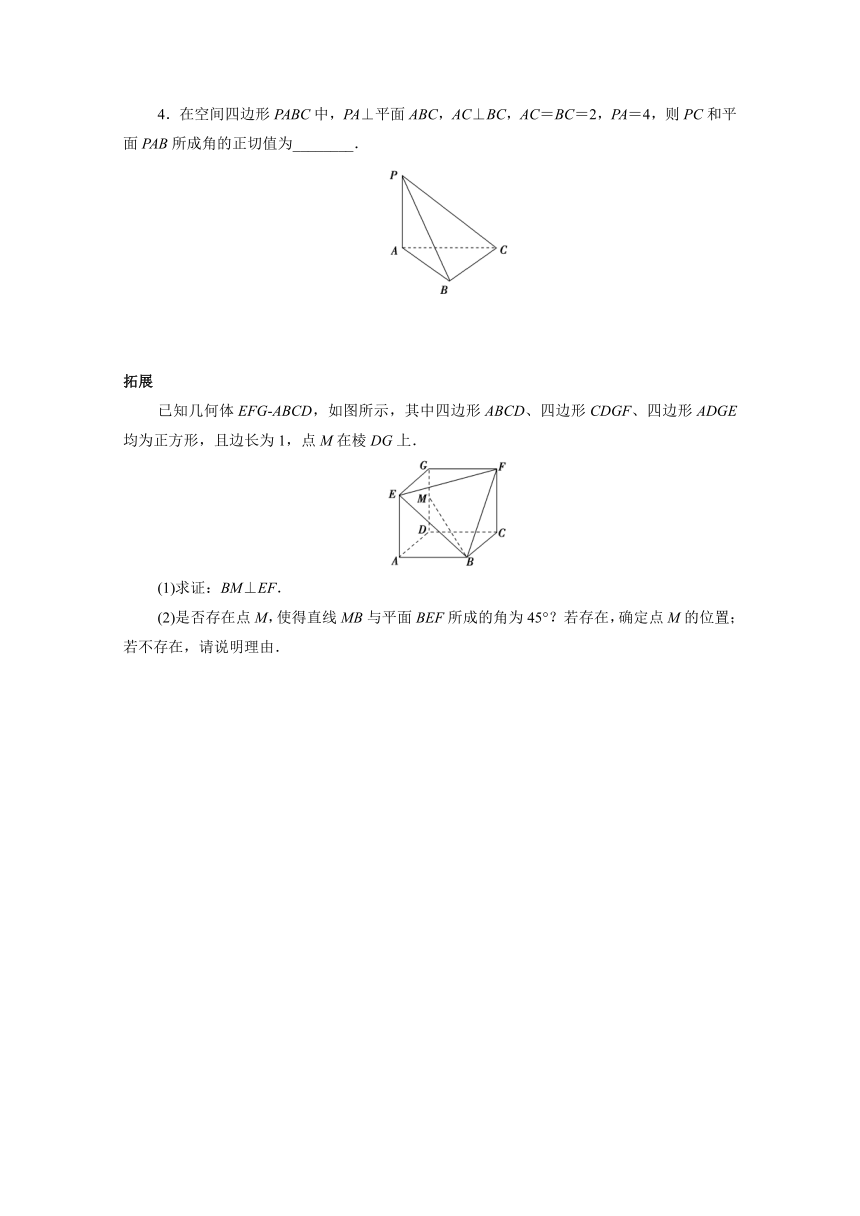
4.在空间四边形PABC中,PA⊥平面ABC,AC⊥BC,AC=BC=2,PA=4,则PC和平面PAB所成角的正切值为________.
拓展
已知几何体EFG ABCD,如图所示,其中四边形ABCD、四边形CDGF、四边形ADGE均为正方形,且边长为1,点M在棱DG上.
(1)求证:BM⊥EF.
(2)是否存在点M,使得直线MB与平面BEF所成的角为45°?若存在,确定点M的位置;若不存在,请说明理由.
参考答案:
基础练
一、选择题
1.在正方体ABCD A1B1C1D1中,直线AD与平面A1BC1所成角的正弦值为( )
A. B. C. D.
C [如图,以D为坐标原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系.设正方体的棱长为1,则平面A1BC1的一个法向量为n=(1,1,1),=(1,0,0),
设直线AD与平面A1BC1所成角为θ,
∴sin θ=|cos〈n,〉|===.]
2.OA,OB,OC是由点O出发的三条射线,两两夹角为60°,则OC与平面OAB所成角的余弦值为( )
A. B. C. D.
B [设OC与平面OAB所成的角为θ,则cos 60°=cos θ·cos 30°,∴cos θ=.]
3.如图,在长方体ABCD A1B1C1D1中,AB=BC=2,若该长方体的体积为8,则直线AC1与平面BB1C1C所成的角为( )
A.30° B.45°
C.60° D.120°
A [∵在长方体ABCD A1B1C1D1中,AB=BC=2,该长方体的体积为8,
∴2×2×AA1=8,解得AA1=2,
以D为坐标原点,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,
A(2,0,0),C1(0,2,2),=(-2,2,2),
平面BB1C1C的一个法向量n=(0,1,0),
设直线AC1与平面BB1C1C所成的角为θ,
sin θ==,∴θ=30°,
∴直线AC1与平面BB1C1C所成的角为30°.故选A.]
4.如图,长方体ABCD A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成角的正弦值为( )
A. B. C. D.
A [以D为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系(图略),则C(0,3,0),E(1,1,0),D1(0,0,1),C1(0,3,1),D(0,0,0),所以=(0,3,1),=(1,1,-1),=(0,3,-1).设平面D1EC的法向量为n=(x,y,z),则即取y=1,可得平面D1EC的一个法向量为n=(2,1,3),所以DC1与平面D1EC所成角的正弦值为==.故选A.]
5.如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则AA1与平面AB1C1所成的角为( )
A. B.
C. D.
A [以C为原点,在平面ABC中过C作BC的垂线为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
则A(,1,0),A1(,1,3),B1(0,2,3),C1(0,0,3),
=(0,0,3),=(-,1,3),=(-,-1,3),
设平面AB1C1的法向量n=(x,y,z),
则
取x=,得n=(,0,1),
设AA1与平面AB1C1所成的角为θ,
则sin θ==,∴θ=.
∴AA1与平面AB1C1所成的角为.故选A.]
二、填空题
6.等腰Rt△ABC的斜边AB在平面α内,若AC与α成30°角,则斜边上的中线CM与平面α所成的角为________.
45° [作CO⊥α,O为垂足,连接AO,MO,则∠CAO=30°,∠CMO为CM与α所成的角.在Rt△AOC中,设CO=1,则AC=2.在等腰Rt△ABC中,由AC=2得CM=.在Rt△CMO中,sin∠CMO===.
∴∠CMO=45°.]
7.如图,在四棱柱ABCD A1B1C1D1中,平面A1B1CD⊥平面ABCD,且四边形ABCD和四边形A1B1CD都是正方形,则直线BD1与平面A1B1CD所成角的正切值是________.
[以D为原点,DA为x轴,DC为y轴,DA1为z轴,建立空间直角坐标系,设AB=1,则B(1,1,0),D1(-1,0,1),
=(-2,-1,1),平面A1B1CD的法向量n=(1,0,0),
设直线BD1与平面A1B1CD所成角为θ,
则sin θ==,
∴cos θ==,
∴直线BD1与平面A1B1CD所成角的正切值是tan θ==.]
8.已知三棱柱ABC A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于________.
[如图,设A1在平面ABC内的射影为O,以O为坐标原点,OA,OA1分别为x轴、z轴,过O作OA的垂线为y轴,建立空间直角坐标系,如图.设△ABC边长为1,则A,
B1,
所以=.
平面ABC的法向量n=(0,0,1),
则AB1与底面ABC所成角α的正弦值为
sin α=|cos〈,n〉|==.]
三、解答题
9.如图,在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E,F分别是PC,AD中点.
(1)求证:DE∥平面PFB;
(2)求PB与平面PCD所成角的正切值.
[解] (1)证明:取PB的中点M,连接EM,FM.
∵E,M分别是PC,PB的中点,
∴EM∥BC,EM=BC,
∵四边形ABCD是正方形,
F是AD的中点,
∴DF∥BC,DF=BC,
∴四边形DEMF是平行四边形,∴DE∥FM,
又DE 平面PFB,FM 平面PFB,
∴DE∥平面PFB.
(2)∵PD⊥平面ABCD,BC 平面ABCD,
∴PD⊥BC,
∵四边形ABCD是正方形,
∴BC⊥CD,
又PD 平面PCD,CD 平面PCD,PD∩CD=D,
∴BC⊥平面PCD.
∴∠BPC为直线PB与平面PCD所成的角,
∵PD=DC=BC,
∴PC=CD=BC,
∴tan∠BPC==.
10.在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,EC=2,F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求直线AD与平面BCE所成角的正弦值.
[解] (1)证明:以A为原点,在平面ACD中,过A作AD的垂线为x轴,AD为y轴,AB为z轴,建立空间直角坐标系,
则A(0,0,0),C(,1,0),
D(0,2,0),F,
B(0,0,1),E(0,2,2),
=,=(,1,-1),=(0,2,1),
设平面BCE的法向量n=(x,y,z),
则
取y=1,得n=(-,1,-2),
∵·n=0,AF 平面BCE,
∴AF∥平面BCE.
(2)=(0,2,0),平面BCE的法向量n=(-,1,-2),
设直线AD与平面BCE所成角为θ,
则sin θ===.
∴直线AD与平面BCE所成角的正弦值为.
能力练
1.(多选题)已知四棱锥P ABCD的四条侧棱都相等,底面是边长为2的正方形,若其五个顶点都在一个表面积为的球面上,则PA与底面ABCD所成角的正弦值为( )
A. B. C. D.
BC [由已知可得,四棱锥P ABCD为正四棱锥,
∵正四棱锥外接球的表面积为,
∴正四棱锥外接球的半径R=.
如图,
连接AC,BD交于E,设球心为O,连接PO,BO,
则E在PO(或其延长线)上,PO=BO=R,
∴BE=BD=×2=,
又R=,OE===.
∴PE=R-OE=-=或PE=R+OE=+=4.
当PE=时,PA==,
PA与底面ABCD所成角的正弦值为=;
当PE=4时,PA==3,
PA与底面ABCD所成角的正弦值为=.
∴PA与底面ABCD所成角的正弦值为或.]
2.在圆柱OO1中,O是上底面圆心,AB是下底面圆的直径,点C在下底面圆周上,若△OAB是正三角形,O1C⊥AB,则OC与平面OAB所成角为( )
A.150° B.30° C.45° D.60°
B [设AB=2a,则OA=2a,O1A=O1B=O1C=a,
∴OO1==a,OC==2a,
∵CO1⊥AB,CO1⊥OO1,AB∩OO1=O1,
∴CO1⊥平面AOB,
∴∠COO1是OC与平面OAB所成角,
sin∠COO1==,∴∠COO1=30°,
∴OC与平面OAB所成角为30°.]
3.在正方体ABCD A1B1C1D1中,E,F分别为AB,BC的中点,则直线CD1与C1F所成角的余弦值为________,直线CD1与平面A1C1FE所成角的正弦值为________.
[以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AB=2,则C(0,2,0),D1(0,0,2),A1(2,0,2),C1(0,2,2),E(2,1,0),F(1,2,0),
∴=(0,-2,2),=(-1,1,0),=(0,-1,2),=(1,0,-2),
cos〈,〉=
===.
设平面A1C1FE的法向量n=(x,y,z),
则取z=1,得n=(2,2,1),
设直线CD1与平面A1C1FE所成角为θ,
则sin θ===.
∴直线CD1与平面A1C1FE所成角的正弦值为.]
4.在空间四边形PABC中,PA⊥平面ABC,AC⊥BC,AC=BC=2,PA=4,则PC和平面PAB所成角的正切值为________.
[取AB的中点为O,连接CO,PO,
∵PA⊥平面ABC,∴PA⊥OC,
∵AC=BC,O是AB的中点,
∴AB⊥OC,
又PA∩AB=A,
∴CO⊥平面PAB,
则∠CPO为PC和平面PAB所成的角.∵AC=BC=2,AC⊥BC,
∴AB=2,CO=AB=,
∴PO==3,
∴tan∠CPO==,
∴PC和平面PAB所成角的正切值为.]
拓展
已知几何体EFG ABCD,如图所示,其中四边形ABCD、四边形CDGF、四边形ADGE均为正方形,且边长为1,点M在棱DG上.
(1)求证:BM⊥EF.
(2)是否存在点M,使得直线MB与平面BEF所成的角为45°?若存在,确定点M的位置;若不存在,请说明理由.
[解] (1)证明:∵四边形ABCD、四边形CDGF、四边形ADGE均为正方形,
∴GD⊥DA,GD⊥DC.
又DA∩DC=D,∴GD⊥平面ABCD.
以点D为坐标原点,建立如图所示的空间直角坐标系Dxyz,
则B(1,1,0),E(1,0,1),F(0,1,1).
点M在棱DG上,故可设M(0,0,t)(0≤t≤1).
∵=(1,1,-t),=(-1,1,0),
∴·=0,∴BM⊥EF.
(2)假设存在点M,使得直线MB与平面BEF所成的角为45°.
设平面BEF的法向量为n=(x,y,z),
∵=(0,-1,1),=(-1,0,1),
∴∴
令z=1,得x=y=1,∴n=(1,1,1)为平面BEF的一个法向量,
∴cos〈n,〉==.
∵直线MB与平面BEF所成的角为45°,
∴sin 45°=|cos〈n,〉|,∴=,
解得t=-4±3.
又0≤t≤1,∴t=3-4,∴存在点M(0,0,3-4).
∴当点M在DG上,且DM=3-4时,直线MB与平面BEF所成的角为45°.
PAGE
(建议用时:40分钟)
基础练
一、选择题
1.在正方体ABCD A1B1C1D1中,直线AD与平面A1BC1所成角的正弦值为( )
A. B. C. D.
2.OA,OB,OC是由点O出发的三条射线,两两夹角为60°,则OC与平面OAB所成角的余弦值为( )
A. B. C. D.
3.如图,在长方体ABCD A1B1C1D1中,AB=BC=2,若该长方体的体积为8,则直线AC1与平面BB1C1C所成的角为( )
A.30° B.45°
C.60° D.120°
4.如图,长方体ABCD A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成角的正弦值为( )
A. B. C. D.
5.如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则AA1与平面AB1C1所成的角为( )
A. B.
C. D.
二、填空题
6.等腰Rt△ABC的斜边AB在平面α内,若AC与α成30°角,则斜边上的中线CM与平面α所成的角为________.
7.如图,在四棱柱ABCD A1B1C1D1中,平面A1B1CD⊥平面ABCD,且四边形ABCD和四边形A1B1CD都是正方形,则直线BD1与平面A1B1CD所成角的正切值是________.
8.已知三棱柱ABC A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于________.
三、解答题
9.如图,在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E,F分别是PC,AD中点.
(1)求证:DE∥平面PFB;
(2)求PB与平面PCD所成角的正切值.
10.在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,EC=2,F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求直线AD与平面BCE所成角的正弦值.
能力练
1.(多选题)已知四棱锥P ABCD的四条侧棱都相等,底面是边长为2的正方形,若其五个顶点都在一个表面积为的球面上,则PA与底面ABCD所成角的正弦值为( )
A. B. C. D.
2.在圆柱OO1中,O是上底面圆心,AB是下底面圆的直径,点C在下底面圆周上,若△OAB是正三角形,O1C⊥AB,则OC与平面OAB所成角为( )
A.150° B.30° C.45° D.60°
3.在正方体ABCD A1B1C1D1中,E,F分别为AB,BC的中点,则直线CD1与C1F所成角的余弦值为________,直线CD1与平面A1C1FE所成角的正弦值为________.
4.在空间四边形PABC中,PA⊥平面ABC,AC⊥BC,AC=BC=2,PA=4,则PC和平面PAB所成角的正切值为________.
拓展
已知几何体EFG ABCD,如图所示,其中四边形ABCD、四边形CDGF、四边形ADGE均为正方形,且边长为1,点M在棱DG上.
(1)求证:BM⊥EF.
(2)是否存在点M,使得直线MB与平面BEF所成的角为45°?若存在,确定点M的位置;若不存在,请说明理由.
参考答案:
基础练
一、选择题
1.在正方体ABCD A1B1C1D1中,直线AD与平面A1BC1所成角的正弦值为( )
A. B. C. D.
C [如图,以D为坐标原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系.设正方体的棱长为1,则平面A1BC1的一个法向量为n=(1,1,1),=(1,0,0),
设直线AD与平面A1BC1所成角为θ,
∴sin θ=|cos〈n,〉|===.]
2.OA,OB,OC是由点O出发的三条射线,两两夹角为60°,则OC与平面OAB所成角的余弦值为( )
A. B. C. D.
B [设OC与平面OAB所成的角为θ,则cos 60°=cos θ·cos 30°,∴cos θ=.]
3.如图,在长方体ABCD A1B1C1D1中,AB=BC=2,若该长方体的体积为8,则直线AC1与平面BB1C1C所成的角为( )
A.30° B.45°
C.60° D.120°
A [∵在长方体ABCD A1B1C1D1中,AB=BC=2,该长方体的体积为8,
∴2×2×AA1=8,解得AA1=2,
以D为坐标原点,DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,
A(2,0,0),C1(0,2,2),=(-2,2,2),
平面BB1C1C的一个法向量n=(0,1,0),
设直线AC1与平面BB1C1C所成的角为θ,
sin θ==,∴θ=30°,
∴直线AC1与平面BB1C1C所成的角为30°.故选A.]
4.如图,长方体ABCD A1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成角的正弦值为( )
A. B. C. D.
A [以D为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系(图略),则C(0,3,0),E(1,1,0),D1(0,0,1),C1(0,3,1),D(0,0,0),所以=(0,3,1),=(1,1,-1),=(0,3,-1).设平面D1EC的法向量为n=(x,y,z),则即取y=1,可得平面D1EC的一个法向量为n=(2,1,3),所以DC1与平面D1EC所成角的正弦值为==.故选A.]
5.如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则AA1与平面AB1C1所成的角为( )
A. B.
C. D.
A [以C为原点,在平面ABC中过C作BC的垂线为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
则A(,1,0),A1(,1,3),B1(0,2,3),C1(0,0,3),
=(0,0,3),=(-,1,3),=(-,-1,3),
设平面AB1C1的法向量n=(x,y,z),
则
取x=,得n=(,0,1),
设AA1与平面AB1C1所成的角为θ,
则sin θ==,∴θ=.
∴AA1与平面AB1C1所成的角为.故选A.]
二、填空题
6.等腰Rt△ABC的斜边AB在平面α内,若AC与α成30°角,则斜边上的中线CM与平面α所成的角为________.
45° [作CO⊥α,O为垂足,连接AO,MO,则∠CAO=30°,∠CMO为CM与α所成的角.在Rt△AOC中,设CO=1,则AC=2.在等腰Rt△ABC中,由AC=2得CM=.在Rt△CMO中,sin∠CMO===.
∴∠CMO=45°.]
7.如图,在四棱柱ABCD A1B1C1D1中,平面A1B1CD⊥平面ABCD,且四边形ABCD和四边形A1B1CD都是正方形,则直线BD1与平面A1B1CD所成角的正切值是________.
[以D为原点,DA为x轴,DC为y轴,DA1为z轴,建立空间直角坐标系,设AB=1,则B(1,1,0),D1(-1,0,1),
=(-2,-1,1),平面A1B1CD的法向量n=(1,0,0),
设直线BD1与平面A1B1CD所成角为θ,
则sin θ==,
∴cos θ==,
∴直线BD1与平面A1B1CD所成角的正切值是tan θ==.]
8.已知三棱柱ABC A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于________.
[如图,设A1在平面ABC内的射影为O,以O为坐标原点,OA,OA1分别为x轴、z轴,过O作OA的垂线为y轴,建立空间直角坐标系,如图.设△ABC边长为1,则A,
B1,
所以=.
平面ABC的法向量n=(0,0,1),
则AB1与底面ABC所成角α的正弦值为
sin α=|cos〈,n〉|==.]
三、解答题
9.如图,在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E,F分别是PC,AD中点.
(1)求证:DE∥平面PFB;
(2)求PB与平面PCD所成角的正切值.
[解] (1)证明:取PB的中点M,连接EM,FM.
∵E,M分别是PC,PB的中点,
∴EM∥BC,EM=BC,
∵四边形ABCD是正方形,
F是AD的中点,
∴DF∥BC,DF=BC,
∴四边形DEMF是平行四边形,∴DE∥FM,
又DE 平面PFB,FM 平面PFB,
∴DE∥平面PFB.
(2)∵PD⊥平面ABCD,BC 平面ABCD,
∴PD⊥BC,
∵四边形ABCD是正方形,
∴BC⊥CD,
又PD 平面PCD,CD 平面PCD,PD∩CD=D,
∴BC⊥平面PCD.
∴∠BPC为直线PB与平面PCD所成的角,
∵PD=DC=BC,
∴PC=CD=BC,
∴tan∠BPC==.
10.在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,EC=2,F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求直线AD与平面BCE所成角的正弦值.
[解] (1)证明:以A为原点,在平面ACD中,过A作AD的垂线为x轴,AD为y轴,AB为z轴,建立空间直角坐标系,
则A(0,0,0),C(,1,0),
D(0,2,0),F,
B(0,0,1),E(0,2,2),
=,=(,1,-1),=(0,2,1),
设平面BCE的法向量n=(x,y,z),
则
取y=1,得n=(-,1,-2),
∵·n=0,AF 平面BCE,
∴AF∥平面BCE.
(2)=(0,2,0),平面BCE的法向量n=(-,1,-2),
设直线AD与平面BCE所成角为θ,
则sin θ===.
∴直线AD与平面BCE所成角的正弦值为.
能力练
1.(多选题)已知四棱锥P ABCD的四条侧棱都相等,底面是边长为2的正方形,若其五个顶点都在一个表面积为的球面上,则PA与底面ABCD所成角的正弦值为( )
A. B. C. D.
BC [由已知可得,四棱锥P ABCD为正四棱锥,
∵正四棱锥外接球的表面积为,
∴正四棱锥外接球的半径R=.
如图,
连接AC,BD交于E,设球心为O,连接PO,BO,
则E在PO(或其延长线)上,PO=BO=R,
∴BE=BD=×2=,
又R=,OE===.
∴PE=R-OE=-=或PE=R+OE=+=4.
当PE=时,PA==,
PA与底面ABCD所成角的正弦值为=;
当PE=4时,PA==3,
PA与底面ABCD所成角的正弦值为=.
∴PA与底面ABCD所成角的正弦值为或.]
2.在圆柱OO1中,O是上底面圆心,AB是下底面圆的直径,点C在下底面圆周上,若△OAB是正三角形,O1C⊥AB,则OC与平面OAB所成角为( )
A.150° B.30° C.45° D.60°
B [设AB=2a,则OA=2a,O1A=O1B=O1C=a,
∴OO1==a,OC==2a,
∵CO1⊥AB,CO1⊥OO1,AB∩OO1=O1,
∴CO1⊥平面AOB,
∴∠COO1是OC与平面OAB所成角,
sin∠COO1==,∴∠COO1=30°,
∴OC与平面OAB所成角为30°.]
3.在正方体ABCD A1B1C1D1中,E,F分别为AB,BC的中点,则直线CD1与C1F所成角的余弦值为________,直线CD1与平面A1C1FE所成角的正弦值为________.
[以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AB=2,则C(0,2,0),D1(0,0,2),A1(2,0,2),C1(0,2,2),E(2,1,0),F(1,2,0),
∴=(0,-2,2),=(-1,1,0),=(0,-1,2),=(1,0,-2),
cos〈,〉=
===.
设平面A1C1FE的法向量n=(x,y,z),
则取z=1,得n=(2,2,1),
设直线CD1与平面A1C1FE所成角为θ,
则sin θ===.
∴直线CD1与平面A1C1FE所成角的正弦值为.]
4.在空间四边形PABC中,PA⊥平面ABC,AC⊥BC,AC=BC=2,PA=4,则PC和平面PAB所成角的正切值为________.
[取AB的中点为O,连接CO,PO,
∵PA⊥平面ABC,∴PA⊥OC,
∵AC=BC,O是AB的中点,
∴AB⊥OC,
又PA∩AB=A,
∴CO⊥平面PAB,
则∠CPO为PC和平面PAB所成的角.∵AC=BC=2,AC⊥BC,
∴AB=2,CO=AB=,
∴PO==3,
∴tan∠CPO==,
∴PC和平面PAB所成角的正切值为.]
拓展
已知几何体EFG ABCD,如图所示,其中四边形ABCD、四边形CDGF、四边形ADGE均为正方形,且边长为1,点M在棱DG上.
(1)求证:BM⊥EF.
(2)是否存在点M,使得直线MB与平面BEF所成的角为45°?若存在,确定点M的位置;若不存在,请说明理由.
[解] (1)证明:∵四边形ABCD、四边形CDGF、四边形ADGE均为正方形,
∴GD⊥DA,GD⊥DC.
又DA∩DC=D,∴GD⊥平面ABCD.
以点D为坐标原点,建立如图所示的空间直角坐标系Dxyz,
则B(1,1,0),E(1,0,1),F(0,1,1).
点M在棱DG上,故可设M(0,0,t)(0≤t≤1).
∵=(1,1,-t),=(-1,1,0),
∴·=0,∴BM⊥EF.
(2)假设存在点M,使得直线MB与平面BEF所成的角为45°.
设平面BEF的法向量为n=(x,y,z),
∵=(0,-1,1),=(-1,0,1),
∴∴
令z=1,得x=y=1,∴n=(1,1,1)为平面BEF的一个法向量,
∴cos〈n,〉==.
∵直线MB与平面BEF所成的角为45°,
∴sin 45°=|cos〈n,〉|,∴=,
解得t=-4±3.
又0≤t≤1,∴t=3-4,∴存在点M(0,0,3-4).
∴当点M在DG上,且DM=3-4时,直线MB与平面BEF所成的角为45°.
PAGE
