2021_2022学年新教材高中数学综合测评 (Word含答案解析)
文档属性
| 名称 | 2021_2022学年新教材高中数学综合测评 (Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 503.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 21:28:12 | ||
图片预览




文档简介
综合测评
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若向量a=(1,0,z)与向量b=(2,1,2)的夹角的余弦值为,则z=( )
A.0 B.1 C.-1 D.2
2.已知四面体ABCD的所有棱长都是2,点E,F分别是AD,DC的中点,则·=( )
A.1 B.-1 C. D.-
3.若A(-2,3),B(3,-2),C三点共线,则m的值为( )
A. B.- C.-2 D.2
4.若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
A.2x-y-5=0 B.2x+y-3=0
C.x+y-1=0 D.x-y-3=0
5.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为( )
A. B. C. D.
6.阿基米德出生于希腊西西里岛叙拉古,享有“力学之父”的美称,和高斯、牛顿并列为世界三大数学家,他利用“逼近法”得到椭圆的面积等于圆周率、椭圆的半长轴长、椭圆的半短轴长三者的乘积.已知椭圆C:+=1(a>b>0)的面积为8π,直线l过椭圆C的两个顶点,且椭圆的中心到直线l的距离为,则椭圆C的方程为( )
A.+=1 B.+=1
C.+y2=1 D.+=1
7.如图所示,在长方体ABCD A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B.
C. D.
8.在棱长为a的正方体ABCD A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是 ( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+3=0,则下列说法正确的是( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=3
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
10.在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P点所作的圆的两条切线相互垂直,则实数k的取值可以是( )
A.1 B.2 C.3 D.4
11.将正方形ABCD沿对角线BD折成直二面角A BD C,则下列结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.AB与平面BCD所成的角为90°
D.AB与CD所成的角为60°
12.设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.|BF|=3 B.△ABF是等边三角形
C.点F到准线的距离为3 D.抛物线C的方程为y2=6x
三、填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.经过两条直线2x+y+2=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0的直线方程为________.
14.从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为________.
15.已知三棱锥A BCD的所有棱长均相等,E为DC的中点,若点P为AC的中点,则直线PE与平面BCD所成角的正弦值为________,若点Q在棱AC所在直线上运动,则直线QE与平面BCD所成角正弦值的最大值为____________
____________________________________________________________________.
(本题第一空2分,第二空3分)
16.已知点F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,|F1F2|=4,点Q(2,)在椭圆C上,P是椭圆C上的动点,则·的最大值为________.
四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)如图,
已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(1)求AB边上的高CE所在直线的方程;
(2)求△ABC的面积.
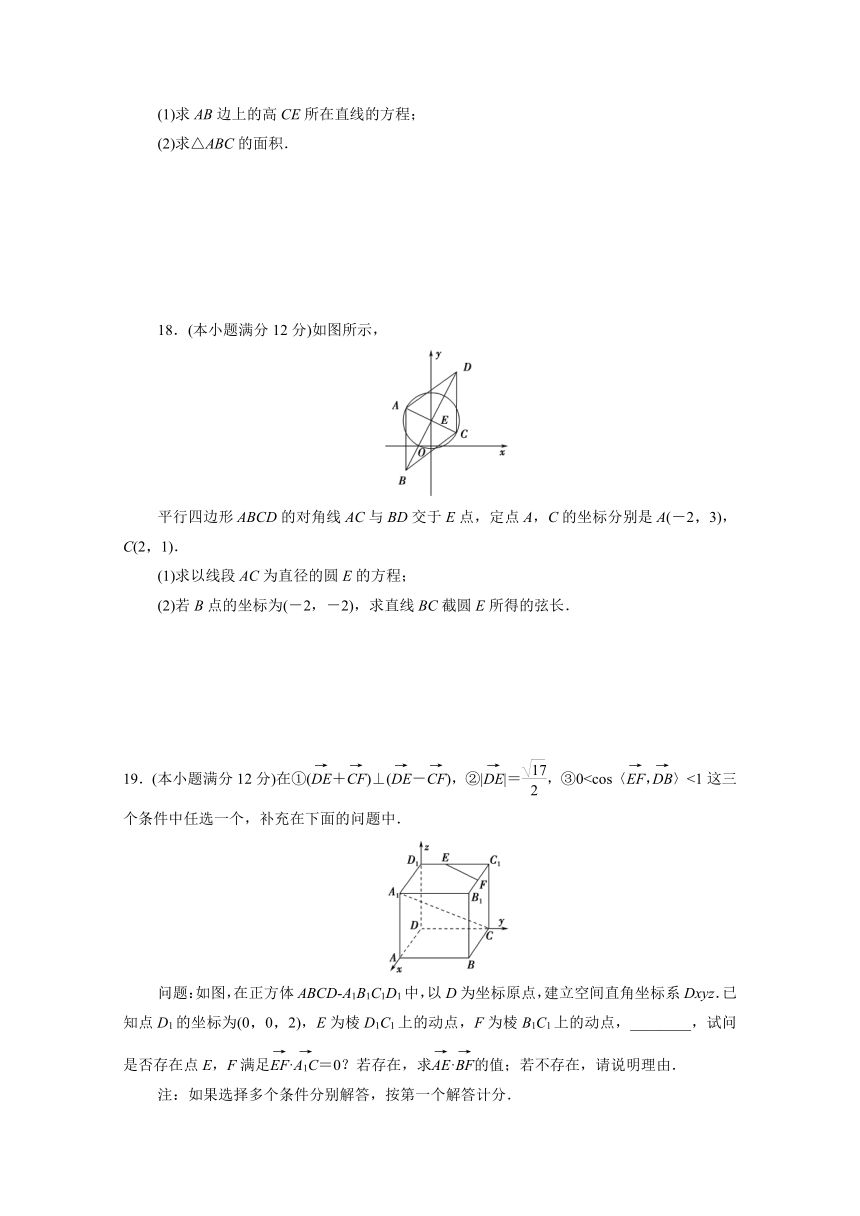
18.(本小题满分12分)如图所示,
平行四边形ABCD的对角线AC与BD交于E点,定点A,C的坐标分别是A(-2,3),C(2,1).
(1)求以线段AC为直径的圆E的方程;
(2)若B点的坐标为(-2,-2),求直线BC截圆E所得的弦长.
19.(本小题满分12分)在①(+)⊥(-),②||=,③0问题:如图,在正方体ABCD A1B1C1D1中,以D为坐标原点,建立空间直角坐标系Dxyz.已知点D1的坐标为(0,0,2),E为棱D1C1上的动点,F为棱B1C1上的动点,________,试问是否存在点E,F满足·=0?若存在,求·的值;若不存在,请说明理由.
注:如果选择多个条件分别解答,按第一个解答计分.
20.(本小题满分12分)已知椭圆C的左、右焦点坐标分别是(-,0),(,0),离心率是,直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
21.(本小题满分12分)如图所示,在四棱锥P ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M为PC的中点,PA=PD=2,BC=AD=1,CD=.
(1)求证:PQ⊥AB;
(2)求二面角P QB M的余弦值.
22.(本小题满分12分)已知圆C:x2+y2+2x-2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.
(1)求抛物线E的方程;
(2)不过原点的动直线l交抛物线E于A,B两点,且满足OA⊥OB.
①求证:直线l过定点;
②设点M为圆C上任意一动点,求当动点M到直线l的距离最大时直线l的方程.
参考答案:
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若向量a=(1,0,z)与向量b=(2,1,2)的夹角的余弦值为,则z=( )
A.0 B.1 C.-1 D.2
A [由题意可知cos〈a,b〉===,解得z=0,故选A.]
2.已知四面体ABCD的所有棱长都是2,点E,F分别是AD,DC的中点,则·=( )
A.1 B.-1 C. D.-
B [
如图所示,=,所以·=·(-)=-×2×2×cos 60°=-1,故选B.]
3.若A(-2,3),B(3,-2),C三点共线,则m的值为( )
A. B.- C.-2 D.2
A [由=,解得m=.]
4.若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
A.2x-y-5=0 B.2x+y-3=0
C.x+y-1=0 D.x-y-3=0
D [圆心C(1,0),kPC==-1,
则kAB=1,AB的方程为y+1=x-2,
即x-y-3=0,故选D.]
5.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为( )
A. B. C. D.
A [抛物线y2=4x的焦点为(1,0),
故双曲线的一个焦点是(1,0),
所以m+n=1,且=2,解得m=,n=,
故mn=.]
6.阿基米德出生于希腊西西里岛叙拉古,享有“力学之父”的美称,和高斯、牛顿并列为世界三大数学家,他利用“逼近法”得到椭圆的面积等于圆周率、椭圆的半长轴长、椭圆的半短轴长三者的乘积.已知椭圆C:+=1(a>b>0)的面积为8π,直线l过椭圆C的两个顶点,且椭圆的中心到直线l的距离为,则椭圆C的方程为( )
A.+=1 B.+=1
C.+y2=1 D.+=1
D [依题意,8π=ab·π,故ab=8. ①
不妨设直线l:+=1,即bx+ay-ab=0,
则椭圆的中心到直线l的距离为=,解得a2+b2=34, ②
联立①②,解得a=4,b=,故椭圆C的方程为+=1.故选D.]
7.如图所示,在长方体ABCD A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B.
C. D.
A [∵B1B⊥平面ABCD,
∴∠BCB1是B1C与底面所成角,
∴∠BCB1=60°.
∵C1C⊥底面ABCD,
∴∠CDC1是C1D与底面所成的角,
∴∠CDC1=45°.
连接A1D,A1C1(图略),则A1D∥B1C.
∴∠A1DC1或其补角为异面直线B1C与C1D所成的角.
不妨设BC=1,则CB1=DA1=2,
BB1=CC1==CD,
∴C1D=,A1C1=2.
在等腰△A1C1D中,cos∠A1DC1==.]
8.在棱长为a的正方体ABCD A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是 ( )
A. B. C. D.
A [建立如图所示的空间直角坐标系,则D(0,0,0),M,
B(a,a,0),A1(a,0,a),
∴=,
=(a,a,0),=(a,0,a).
设平面MBD的法向量为n=(x,y,z),
则令x=1,则可得n=(1,-1,-2).
∴d===a.]
二、选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+3=0,则下列说法正确的是( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=3
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
BD [直线l1∥l2,则3-m(m-2)=0,解得m=3或m=-1,但m=-1时,两直线方程分别为x-y-1=0,-3x+3y+3=0即x-y-1=0,两直线重合,只有m=3时两直线平行,A错,B正确;l1⊥l2,则m-2+3m=0,m=,C错,D正确.故选BD.]
10.在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P点所作的圆的两条切线相互垂直,则实数k的取值可以是( )
A.1 B.2 C.3 D.4
AB [圆C的方程为x2+y2-4x=0,则圆心为C(2,0),半径r=2.
设两个切点分别为A,B,则由题意可得四边形PACB为正方形,故有PC=r=2,
∴圆心到直线y=k(x+1)的距离小于或等于PC,
即≤2,解得k2≤8,可得-2≤k≤2,
∴结合选项,实数k的取值可以是1,2.]
11.将正方形ABCD沿对角线BD折成直二面角A BD C,则下列结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.AB与平面BCD所成的角为90°
D.AB与CD所成的角为60°
ABD [如图,取BD的中点O,连接AO,CO,AC,则AO⊥BD,CO⊥BD,
又AO∩CO=O,∴BD⊥平面AOC,又AC 平面AOC,∴AC⊥BD,A正确;∵AC=AO=AD=CD,∴△ACD是等边三角形,B正确;易知AO⊥平面BCD,∴∠ABD是AB与平面BCD所成的角,为45°,C错误;∵=++,不妨设AB=1,则=(++)2=+++2·+2·+2·,∴1=1+2+1+2×+2×+2cos〈,〉,∴cos〈,〉=,∴AB与CD所成的角为60°,D正确.故选ABD.]
12.设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.|BF|=3 B.△ABF是等边三角形
C.点F到准线的距离为3 D.抛物线C的方程为y2=6x
BCD [因为|FA|为半径的圆交l于B,D两点,所以FA=FB,若∠ABD=90°,可得FA=AB,所以可得△ABF为等边三角形,所以B正确;过F作FC⊥AB交AB于C,则C为AB的中点,C的横坐标为,B的横坐标为-,所以A的横坐标为,代入抛物线可得y2=3p2,|yA|=p,△ABF的面积为9,即(xA-xB)·|yA|=××p=9,解得p=3,
所以抛物线的方程为y2=6x,所以D正确;
焦点坐标为,所以焦点到准线的距离为×2=3,所以C正确;
此时A点的横坐标为,所以BF=AF=AB=+=6,所以A不正确.]
三、填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.经过两条直线2x+y+2=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0的直线方程为________.
2x+3y-2=0 [由方程组得交点A(-2,2),因为所求直线垂直于直线3x-2y+4=0,故所求直线的斜率k=-,由点斜式得所求直线方程为y-2=-(x+2),即2x+3y-2=0.]
14.从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为________.
2π [(数形结合法)如图,
圆x2+y2-12y+27=0可化为x2+(y-6)2=9,圆心坐标为(0,6),半径为3.
在Rt△OBC中可得∠OCB=,
∴∠ACB=,∴所求劣弧长为2π.]
15.已知三棱锥A BCD的所有棱长均相等,E为DC的中点,若点P为AC的中点,则直线PE与平面BCD所成角的正弦值为________,若点Q在棱AC所在直线上运动,则直线QE与平面BCD所成角正弦值的最大值为____________
____________________________________________________________________.
(本题第一空2分,第二空3分)
[连接BE,AE,过A作AO⊥底面BCD,垂足为O,连接OD,则∠ADO是直线PE与平面BCD所成角(图略),
因三棱锥A BCD的所有棱长均相等,设棱长为2,
则DO=BO=BE==,
AO==,
∴sin∠ADO===.
∴直线PE与平面BCD所成角的正弦值为.
当Q与A重合时,直线QE与平面BCD所成角正弦值取最大值,此时直线QE与平面BCD所成角为∠AEO,AE==,
∴直线QE与平面BCD所成角正弦值的最大值为sin∠AEO===.]
16.已知点F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,|F1F2|=4,点Q(2,)在椭圆C上,P是椭圆C上的动点,则·的最大值为________.
[由题意可得c=2,+=1,a2=b2+c2,解得a2=8,b2=4,
所以椭圆C的方程为+=1,
可得F1(-2,0),
设P(x,y),由+=1,可得x2=8-2y2,
则·=(2-x,-y)(-2-x,-y)=x2-4+y2-y=-y2-y+4=-++4,当且仅当y=-∈[-2,2]时,
·取得最大值为.]
四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)如图,
已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(1)求AB边上的高CE所在直线的方程;
(2)求△ABC的面积.
[解] (1)由题意可知,E为AB的中点,
∴E(3,2),且kCE=-=1,
∴CE所在直线方程为y-2=x-3,即x-y-1=0.
(2)由得C(4,3),
∴|AC|=|BC|=2,AC⊥BC,
∴S△ABC=|AC|·|BC|=2.
18.(本小题满分12分)如图所示,
平行四边形ABCD的对角线AC与BD交于E点,定点A,C的坐标分别是A(-2,3),C(2,1).
(1)求以线段AC为直径的圆E的方程;
(2)若B点的坐标为(-2,-2),求直线BC截圆E所得的弦长.
[解] (1)AC的中点E(0,2)即为圆心,
半径r=|AC|==,
所以圆E的方程为x2+(y-2)2=5.
(2)直线BC的斜率k==,
其方程为y-1=(x-2),即3x-4y-2=0.
点E到直线BC的距离为d==2,所以BC截圆E所得的弦长为2=2.
19.(本小题满分12分)在①(+)⊥(-),②||=,③0问题:如图,在正方体ABCD A1B1C1D1中,以D为坐标原点,建立空间直角坐标系Dxyz.已知点D1的坐标为(0,0,2),E为棱D1C1上的动点,F为棱B1C1上的动点,________,试问是否存在点E,F满足·=0?若存在,求·的值;若不存在,请说明理由.
注:如果选择多个条件分别解答,按第一个解答计分.
[解] 由题意,正方体ABCD A1B1C1D1的棱长为2.
则A(2,0,0),B(2,2,0),A1(2,0,2),D(0,0,0),C(0,2,0),
设E(0,a,2)(0≤a≤2),F(b,2,2)(0≤b≤2),
则=(b,2-a,0),=(-2,2,-2),=(-2,a,2),=(b-2,0,2),
所以·=4-2(a+b),·=8-2b.
选择①,因为(+)⊥(-),所以(+)·(-)=2-2=0,即2=2,
即0+(a-0)2+(2-0)2=(b-0)2+(2-2)2+(2-0)2,所以a=b.
因为·=4-2×(a+b)=0,所以a=b=1,
故存在点E(0,1,2),F(1,2,2),满足·=0,且·=8-2b=6.
选择②,||=,即=,a=,
因为·=4-2(a+b)=0,所以b=,
故存在点E,F,
满足·=0,且·=8-2b=5.
选择③,=(b,2-a,0),=(2,2,0),
因为0<cos〈,〉<1,所以与不共线,
所以b≠2-a,即a+b≠2,则·=4-2(a+b)≠0,
故不存在点E,F满足·=0.
20.(本小题满分12分)已知椭圆C的左、右焦点坐标分别是(-,0),(,0),离心率是,直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
[解] (1)因为=,且c=,
所以a=,b==1,
所以椭圆C的方程为+y2=1.
(2)由题意知P(0,t)(-1<t<1).
由得x=±,
所以圆P的半径为.
当圆P与x轴相切时,
|t|=,解得t=±.
所以点P的坐标是.
21.(本小题满分12分)如图所示,在四棱锥P ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M为PC的中点,PA=PD=2,BC=AD=1,CD=.
(1)求证:PQ⊥AB;
(2)求二面角P QB M的余弦值.
[解] (1)证明:在△PAD中,PA=PD,Q为AD的中点,所以PQ⊥AD.
因为平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PQ⊥底面ABCD.
又AB 平面ABCD,所以PQ⊥AB.
(2)在直角梯形ABCD中,AD∥BC,BC=AD,Q为AD的中点,
所以四边形BCDQ为平行四边形.
因为AD⊥DC,所以AD⊥QB.
由(1),可知PQ⊥平面ABCD,故以Q为坐标原点,建立空间直角坐标系Qxyz如图所示,则Q(0,0,0),A(1,0,0),P(0,0,),C(-1,,0),B(0,,0),=(0,,0).
因为AQ⊥PQ,AQ⊥BQ,所以AQ⊥平面PQB,
即为平面PQB的一个法向量,且=(1,0,0).
因为M是棱PC的中点,所以点M的坐标为,所以=.
设平面MQB的法向量为m=(x,y,z),
则即
令z=1,得x=,y=0,所以m=(,0,1),
所以cos〈,m〉==.
由题意知,二面角P QB M为锐角,
所以二面角P QB M的余弦值为.
22.(本小题满分12分)已知圆C:x2+y2+2x-2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.
(1)求抛物线E的方程;
(2)不过原点的动直线l交抛物线E于A,B两点,且满足OA⊥OB.
①求证:直线l过定点;
②设点M为圆C上任意一动点,求当动点M到直线l的距离最大时直线l的方程.
[解] (1)圆C:x2+y2+2x-2y+1=0,
可得圆心C(-1,1),半径r=1,
抛物线E:y2=2px(p>0)的焦点F,准线方程为x=-,圆心C到抛物线焦点F的距离为,
即有=,
解得p=6,即抛物线方程为y2=12x.
(2)①证明:设直线l的方程为x=my+t,A(x1,y1),
B(x2,y2),则
整理得:y2-12my-12t=0,
所以y1+y2=12m,y1y2=-12t.
由于OA⊥OB,则x1x2+y1y2=0.
即(m2+1)y1y2+mt(y1+y2)+t2=0.
整理得t2-12t=0,由于t≠0,解得t=12.
故直线的方程为x=my+12,
直线经过定点P(12,0).
②当CP⊥l且动点M经过PC的延长线时,动点M到动直线l的距离取得最大值.
kMP=kCP=-,则m=.
此时直线l的方程为x=y+12,
即13x-y-156=0.
PAGE
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若向量a=(1,0,z)与向量b=(2,1,2)的夹角的余弦值为,则z=( )
A.0 B.1 C.-1 D.2
2.已知四面体ABCD的所有棱长都是2,点E,F分别是AD,DC的中点,则·=( )
A.1 B.-1 C. D.-
3.若A(-2,3),B(3,-2),C三点共线,则m的值为( )
A. B.- C.-2 D.2
4.若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
A.2x-y-5=0 B.2x+y-3=0
C.x+y-1=0 D.x-y-3=0
5.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为( )
A. B. C. D.
6.阿基米德出生于希腊西西里岛叙拉古,享有“力学之父”的美称,和高斯、牛顿并列为世界三大数学家,他利用“逼近法”得到椭圆的面积等于圆周率、椭圆的半长轴长、椭圆的半短轴长三者的乘积.已知椭圆C:+=1(a>b>0)的面积为8π,直线l过椭圆C的两个顶点,且椭圆的中心到直线l的距离为,则椭圆C的方程为( )
A.+=1 B.+=1
C.+y2=1 D.+=1
7.如图所示,在长方体ABCD A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B.
C. D.
8.在棱长为a的正方体ABCD A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是 ( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+3=0,则下列说法正确的是( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=3
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
10.在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P点所作的圆的两条切线相互垂直,则实数k的取值可以是( )
A.1 B.2 C.3 D.4
11.将正方形ABCD沿对角线BD折成直二面角A BD C,则下列结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.AB与平面BCD所成的角为90°
D.AB与CD所成的角为60°
12.设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.|BF|=3 B.△ABF是等边三角形
C.点F到准线的距离为3 D.抛物线C的方程为y2=6x
三、填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.经过两条直线2x+y+2=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0的直线方程为________.
14.从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为________.
15.已知三棱锥A BCD的所有棱长均相等,E为DC的中点,若点P为AC的中点,则直线PE与平面BCD所成角的正弦值为________,若点Q在棱AC所在直线上运动,则直线QE与平面BCD所成角正弦值的最大值为____________
____________________________________________________________________.
(本题第一空2分,第二空3分)
16.已知点F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,|F1F2|=4,点Q(2,)在椭圆C上,P是椭圆C上的动点,则·的最大值为________.
四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)如图,
已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(1)求AB边上的高CE所在直线的方程;
(2)求△ABC的面积.
18.(本小题满分12分)如图所示,
平行四边形ABCD的对角线AC与BD交于E点,定点A,C的坐标分别是A(-2,3),C(2,1).
(1)求以线段AC为直径的圆E的方程;
(2)若B点的坐标为(-2,-2),求直线BC截圆E所得的弦长.
19.(本小题满分12分)在①(+)⊥(-),②||=,③0
注:如果选择多个条件分别解答,按第一个解答计分.
20.(本小题满分12分)已知椭圆C的左、右焦点坐标分别是(-,0),(,0),离心率是,直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
21.(本小题满分12分)如图所示,在四棱锥P ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M为PC的中点,PA=PD=2,BC=AD=1,CD=.
(1)求证:PQ⊥AB;
(2)求二面角P QB M的余弦值.
22.(本小题满分12分)已知圆C:x2+y2+2x-2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.
(1)求抛物线E的方程;
(2)不过原点的动直线l交抛物线E于A,B两点,且满足OA⊥OB.
①求证:直线l过定点;
②设点M为圆C上任意一动点,求当动点M到直线l的距离最大时直线l的方程.
参考答案:
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若向量a=(1,0,z)与向量b=(2,1,2)的夹角的余弦值为,则z=( )
A.0 B.1 C.-1 D.2
A [由题意可知cos〈a,b〉===,解得z=0,故选A.]
2.已知四面体ABCD的所有棱长都是2,点E,F分别是AD,DC的中点,则·=( )
A.1 B.-1 C. D.-
B [
如图所示,=,所以·=·(-)=-×2×2×cos 60°=-1,故选B.]
3.若A(-2,3),B(3,-2),C三点共线,则m的值为( )
A. B.- C.-2 D.2
A [由=,解得m=.]
4.若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
A.2x-y-5=0 B.2x+y-3=0
C.x+y-1=0 D.x-y-3=0
D [圆心C(1,0),kPC==-1,
则kAB=1,AB的方程为y+1=x-2,
即x-y-3=0,故选D.]
5.双曲线-=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为( )
A. B. C. D.
A [抛物线y2=4x的焦点为(1,0),
故双曲线的一个焦点是(1,0),
所以m+n=1,且=2,解得m=,n=,
故mn=.]
6.阿基米德出生于希腊西西里岛叙拉古,享有“力学之父”的美称,和高斯、牛顿并列为世界三大数学家,他利用“逼近法”得到椭圆的面积等于圆周率、椭圆的半长轴长、椭圆的半短轴长三者的乘积.已知椭圆C:+=1(a>b>0)的面积为8π,直线l过椭圆C的两个顶点,且椭圆的中心到直线l的距离为,则椭圆C的方程为( )
A.+=1 B.+=1
C.+y2=1 D.+=1
D [依题意,8π=ab·π,故ab=8. ①
不妨设直线l:+=1,即bx+ay-ab=0,
则椭圆的中心到直线l的距离为=,解得a2+b2=34, ②
联立①②,解得a=4,b=,故椭圆C的方程为+=1.故选D.]
7.如图所示,在长方体ABCD A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B.
C. D.
A [∵B1B⊥平面ABCD,
∴∠BCB1是B1C与底面所成角,
∴∠BCB1=60°.
∵C1C⊥底面ABCD,
∴∠CDC1是C1D与底面所成的角,
∴∠CDC1=45°.
连接A1D,A1C1(图略),则A1D∥B1C.
∴∠A1DC1或其补角为异面直线B1C与C1D所成的角.
不妨设BC=1,则CB1=DA1=2,
BB1=CC1==CD,
∴C1D=,A1C1=2.
在等腰△A1C1D中,cos∠A1DC1==.]
8.在棱长为a的正方体ABCD A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是 ( )
A. B. C. D.
A [建立如图所示的空间直角坐标系,则D(0,0,0),M,
B(a,a,0),A1(a,0,a),
∴=,
=(a,a,0),=(a,0,a).
设平面MBD的法向量为n=(x,y,z),
则令x=1,则可得n=(1,-1,-2).
∴d===a.]
二、选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.已知直线l1:x+my-1=0,l2:(m-2)x+3y+3=0,则下列说法正确的是( )
A.若l1∥l2,则m=-1或m=3
B.若l1∥l2,则m=3
C.若l1⊥l2,则m=-
D.若l1⊥l2,则m=
BD [直线l1∥l2,则3-m(m-2)=0,解得m=3或m=-1,但m=-1时,两直线方程分别为x-y-1=0,-3x+3y+3=0即x-y-1=0,两直线重合,只有m=3时两直线平行,A错,B正确;l1⊥l2,则m-2+3m=0,m=,C错,D正确.故选BD.]
10.在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P点所作的圆的两条切线相互垂直,则实数k的取值可以是( )
A.1 B.2 C.3 D.4
AB [圆C的方程为x2+y2-4x=0,则圆心为C(2,0),半径r=2.
设两个切点分别为A,B,则由题意可得四边形PACB为正方形,故有PC=r=2,
∴圆心到直线y=k(x+1)的距离小于或等于PC,
即≤2,解得k2≤8,可得-2≤k≤2,
∴结合选项,实数k的取值可以是1,2.]
11.将正方形ABCD沿对角线BD折成直二面角A BD C,则下列结论正确的是( )
A.AC⊥BD
B.△ACD是等边三角形
C.AB与平面BCD所成的角为90°
D.AB与CD所成的角为60°
ABD [如图,取BD的中点O,连接AO,CO,AC,则AO⊥BD,CO⊥BD,
又AO∩CO=O,∴BD⊥平面AOC,又AC 平面AOC,∴AC⊥BD,A正确;∵AC=AO=AD=CD,∴△ACD是等边三角形,B正确;易知AO⊥平面BCD,∴∠ABD是AB与平面BCD所成的角,为45°,C错误;∵=++,不妨设AB=1,则=(++)2=+++2·+2·+2·,∴1=1+2+1+2×+2×+2cos〈,〉,∴cos〈,〉=,∴AB与CD所成的角为60°,D正确.故选ABD.]
12.设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若∠ABD=90°,且△ABF的面积为9,则( )
A.|BF|=3 B.△ABF是等边三角形
C.点F到准线的距离为3 D.抛物线C的方程为y2=6x
BCD [因为|FA|为半径的圆交l于B,D两点,所以FA=FB,若∠ABD=90°,可得FA=AB,所以可得△ABF为等边三角形,所以B正确;过F作FC⊥AB交AB于C,则C为AB的中点,C的横坐标为,B的横坐标为-,所以A的横坐标为,代入抛物线可得y2=3p2,|yA|=p,△ABF的面积为9,即(xA-xB)·|yA|=××p=9,解得p=3,
所以抛物线的方程为y2=6x,所以D正确;
焦点坐标为,所以焦点到准线的距离为×2=3,所以C正确;
此时A点的横坐标为,所以BF=AF=AB=+=6,所以A不正确.]
三、填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.经过两条直线2x+y+2=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0的直线方程为________.
2x+3y-2=0 [由方程组得交点A(-2,2),因为所求直线垂直于直线3x-2y+4=0,故所求直线的斜率k=-,由点斜式得所求直线方程为y-2=-(x+2),即2x+3y-2=0.]
14.从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为________.
2π [(数形结合法)如图,
圆x2+y2-12y+27=0可化为x2+(y-6)2=9,圆心坐标为(0,6),半径为3.
在Rt△OBC中可得∠OCB=,
∴∠ACB=,∴所求劣弧长为2π.]
15.已知三棱锥A BCD的所有棱长均相等,E为DC的中点,若点P为AC的中点,则直线PE与平面BCD所成角的正弦值为________,若点Q在棱AC所在直线上运动,则直线QE与平面BCD所成角正弦值的最大值为____________
____________________________________________________________________.
(本题第一空2分,第二空3分)
[连接BE,AE,过A作AO⊥底面BCD,垂足为O,连接OD,则∠ADO是直线PE与平面BCD所成角(图略),
因三棱锥A BCD的所有棱长均相等,设棱长为2,
则DO=BO=BE==,
AO==,
∴sin∠ADO===.
∴直线PE与平面BCD所成角的正弦值为.
当Q与A重合时,直线QE与平面BCD所成角正弦值取最大值,此时直线QE与平面BCD所成角为∠AEO,AE==,
∴直线QE与平面BCD所成角正弦值的最大值为sin∠AEO===.]
16.已知点F1,F2是椭圆C:+=1(a>b>0)的左、右焦点,|F1F2|=4,点Q(2,)在椭圆C上,P是椭圆C上的动点,则·的最大值为________.
[由题意可得c=2,+=1,a2=b2+c2,解得a2=8,b2=4,
所以椭圆C的方程为+=1,
可得F1(-2,0),
设P(x,y),由+=1,可得x2=8-2y2,
则·=(2-x,-y)(-2-x,-y)=x2-4+y2-y=-y2-y+4=-++4,当且仅当y=-∈[-2,2]时,
·取得最大值为.]
四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)如图,
已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(1)求AB边上的高CE所在直线的方程;
(2)求△ABC的面积.
[解] (1)由题意可知,E为AB的中点,
∴E(3,2),且kCE=-=1,
∴CE所在直线方程为y-2=x-3,即x-y-1=0.
(2)由得C(4,3),
∴|AC|=|BC|=2,AC⊥BC,
∴S△ABC=|AC|·|BC|=2.
18.(本小题满分12分)如图所示,
平行四边形ABCD的对角线AC与BD交于E点,定点A,C的坐标分别是A(-2,3),C(2,1).
(1)求以线段AC为直径的圆E的方程;
(2)若B点的坐标为(-2,-2),求直线BC截圆E所得的弦长.
[解] (1)AC的中点E(0,2)即为圆心,
半径r=|AC|==,
所以圆E的方程为x2+(y-2)2=5.
(2)直线BC的斜率k==,
其方程为y-1=(x-2),即3x-4y-2=0.
点E到直线BC的距离为d==2,所以BC截圆E所得的弦长为2=2.
19.(本小题满分12分)在①(+)⊥(-),②||=,③0
注:如果选择多个条件分别解答,按第一个解答计分.
[解] 由题意,正方体ABCD A1B1C1D1的棱长为2.
则A(2,0,0),B(2,2,0),A1(2,0,2),D(0,0,0),C(0,2,0),
设E(0,a,2)(0≤a≤2),F(b,2,2)(0≤b≤2),
则=(b,2-a,0),=(-2,2,-2),=(-2,a,2),=(b-2,0,2),
所以·=4-2(a+b),·=8-2b.
选择①,因为(+)⊥(-),所以(+)·(-)=2-2=0,即2=2,
即0+(a-0)2+(2-0)2=(b-0)2+(2-2)2+(2-0)2,所以a=b.
因为·=4-2×(a+b)=0,所以a=b=1,
故存在点E(0,1,2),F(1,2,2),满足·=0,且·=8-2b=6.
选择②,||=,即=,a=,
因为·=4-2(a+b)=0,所以b=,
故存在点E,F,
满足·=0,且·=8-2b=5.
选择③,=(b,2-a,0),=(2,2,0),
因为0<cos〈,〉<1,所以与不共线,
所以b≠2-a,即a+b≠2,则·=4-2(a+b)≠0,
故不存在点E,F满足·=0.
20.(本小题满分12分)已知椭圆C的左、右焦点坐标分别是(-,0),(,0),离心率是,直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(1)求椭圆C的方程;
(2)若圆P与x轴相切,求圆心P的坐标.
[解] (1)因为=,且c=,
所以a=,b==1,
所以椭圆C的方程为+y2=1.
(2)由题意知P(0,t)(-1<t<1).
由得x=±,
所以圆P的半径为.
当圆P与x轴相切时,
|t|=,解得t=±.
所以点P的坐标是.
21.(本小题满分12分)如图所示,在四棱锥P ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,平面PAD⊥底面ABCD,Q为AD的中点,M为PC的中点,PA=PD=2,BC=AD=1,CD=.
(1)求证:PQ⊥AB;
(2)求二面角P QB M的余弦值.
[解] (1)证明:在△PAD中,PA=PD,Q为AD的中点,所以PQ⊥AD.
因为平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PQ⊥底面ABCD.
又AB 平面ABCD,所以PQ⊥AB.
(2)在直角梯形ABCD中,AD∥BC,BC=AD,Q为AD的中点,
所以四边形BCDQ为平行四边形.
因为AD⊥DC,所以AD⊥QB.
由(1),可知PQ⊥平面ABCD,故以Q为坐标原点,建立空间直角坐标系Qxyz如图所示,则Q(0,0,0),A(1,0,0),P(0,0,),C(-1,,0),B(0,,0),=(0,,0).
因为AQ⊥PQ,AQ⊥BQ,所以AQ⊥平面PQB,
即为平面PQB的一个法向量,且=(1,0,0).
因为M是棱PC的中点,所以点M的坐标为,所以=.
设平面MQB的法向量为m=(x,y,z),
则即
令z=1,得x=,y=0,所以m=(,0,1),
所以cos〈,m〉==.
由题意知,二面角P QB M为锐角,
所以二面角P QB M的余弦值为.
22.(本小题满分12分)已知圆C:x2+y2+2x-2y+1=0和抛物线E:y2=2px(p>0),圆心C到抛物线焦点F的距离为.
(1)求抛物线E的方程;
(2)不过原点的动直线l交抛物线E于A,B两点,且满足OA⊥OB.
①求证:直线l过定点;
②设点M为圆C上任意一动点,求当动点M到直线l的距离最大时直线l的方程.
[解] (1)圆C:x2+y2+2x-2y+1=0,
可得圆心C(-1,1),半径r=1,
抛物线E:y2=2px(p>0)的焦点F,准线方程为x=-,圆心C到抛物线焦点F的距离为,
即有=,
解得p=6,即抛物线方程为y2=12x.
(2)①证明:设直线l的方程为x=my+t,A(x1,y1),
B(x2,y2),则
整理得:y2-12my-12t=0,
所以y1+y2=12m,y1y2=-12t.
由于OA⊥OB,则x1x2+y1y2=0.
即(m2+1)y1y2+mt(y1+y2)+t2=0.
整理得t2-12t=0,由于t≠0,解得t=12.
故直线的方程为x=my+12,
直线经过定点P(12,0).
②当CP⊥l且动点M经过PC的延长线时,动点M到动直线l的距离取得最大值.
kMP=kCP=-,则m=.
此时直线l的方程为x=y+12,
即13x-y-156=0.
PAGE
