13.1.1轴对称练习题(人教版数学八年级上期)(word版含答案)
文档属性
| 名称 | 13.1.1轴对称练习题(人教版数学八年级上期)(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 10:13:30 | ||
图片预览


文档简介
人教版数学八年级上期
13.1.1轴对称练习题
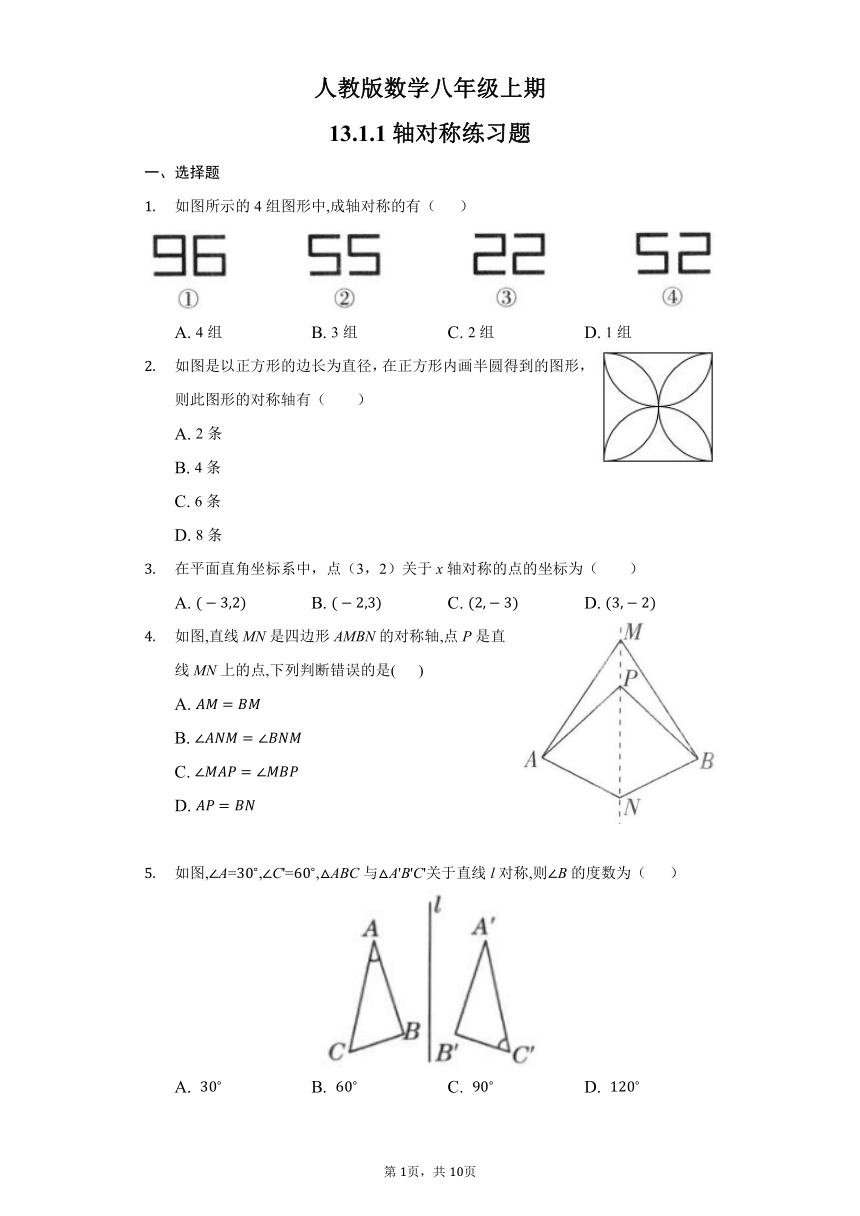
一、选择题
如图所示的4组图形中,成轴对称的有( )
A. 4组 B. 3组 C. 2组 D. 1组
如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A. 2条
B. 4条
C. 6条
D. 8条
在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为( )
A. B. C. D.
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.
B.
C.
D.
如图,A=,C'=,ABC与A'B'C'关于直线l对称,则B的度数为( )
A. B. C. D.
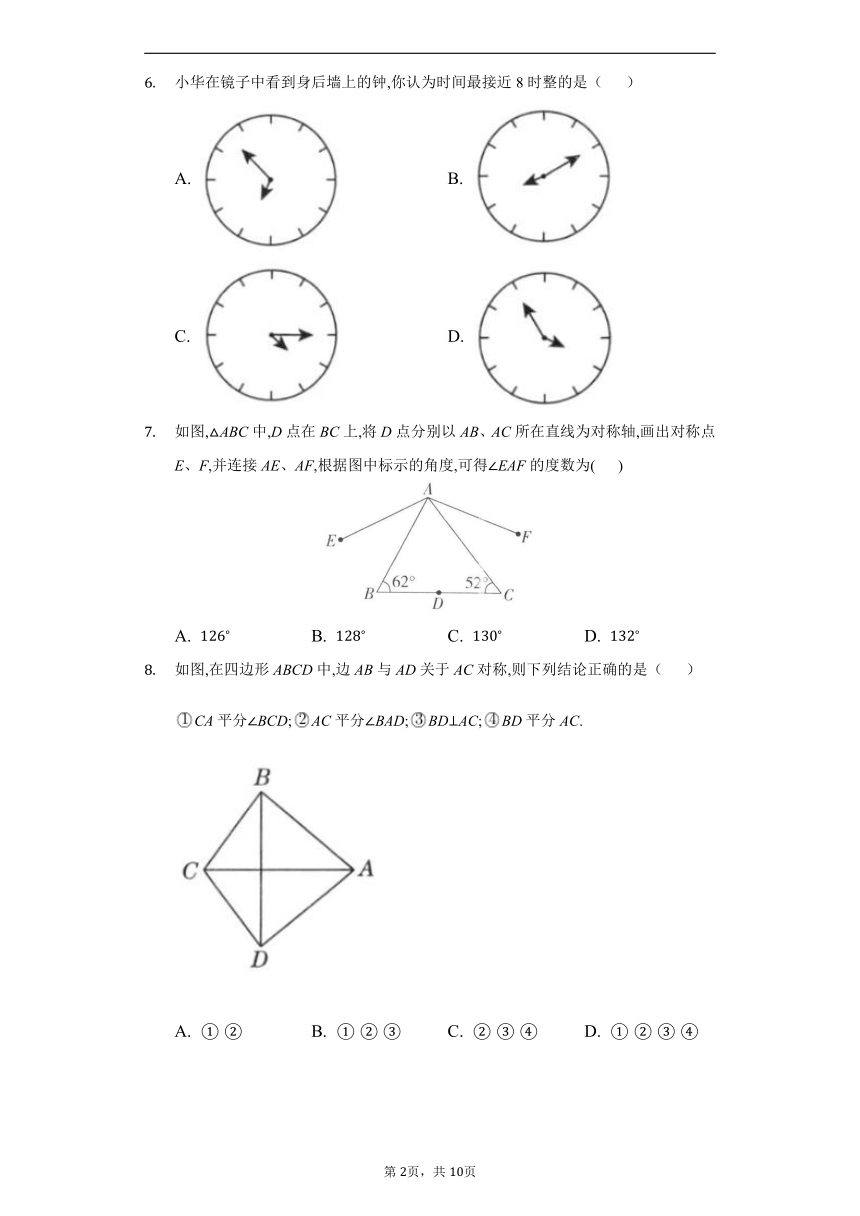
小华在镜子中看到身后墙上的钟,你认为时间最接近8时整的是( )
A. B.
C. D.
如图,ABC中,D点在BC上,将D点分别以AB、AC所在直线为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,可得EAF的度数为( )
A. B. C. D.
如图,在四边形ABCD中,边AB与AD关于AC对称,则下列结论正确的是( )
CA平分BCD;AC平分BAD;BDAC;BD平分AC.
A. B. C. D.
二、填空题
如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为______.
如图,在ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若ABC的面积为,则图中阴影部分的面积是 .
如图,从汽车的后视镜中看见某车牌的5位号码的车牌号为____________.
如图,四边形ABCD的对称轴是AD所在的直线,AC=5,DB=7,则四边形ABCD的周长为______.
如图,是一个风筝的图案,它是轴对称图形,EF是对称轴,∠A=90°,∠AED=120°,∠C=50°,则∠BFC的度数为____.
如图是小明制作的风筝,为了平衡做成了轴对称图形.已知OC所在直线是对称轴,A=,BCO=,那么AOB=__________.
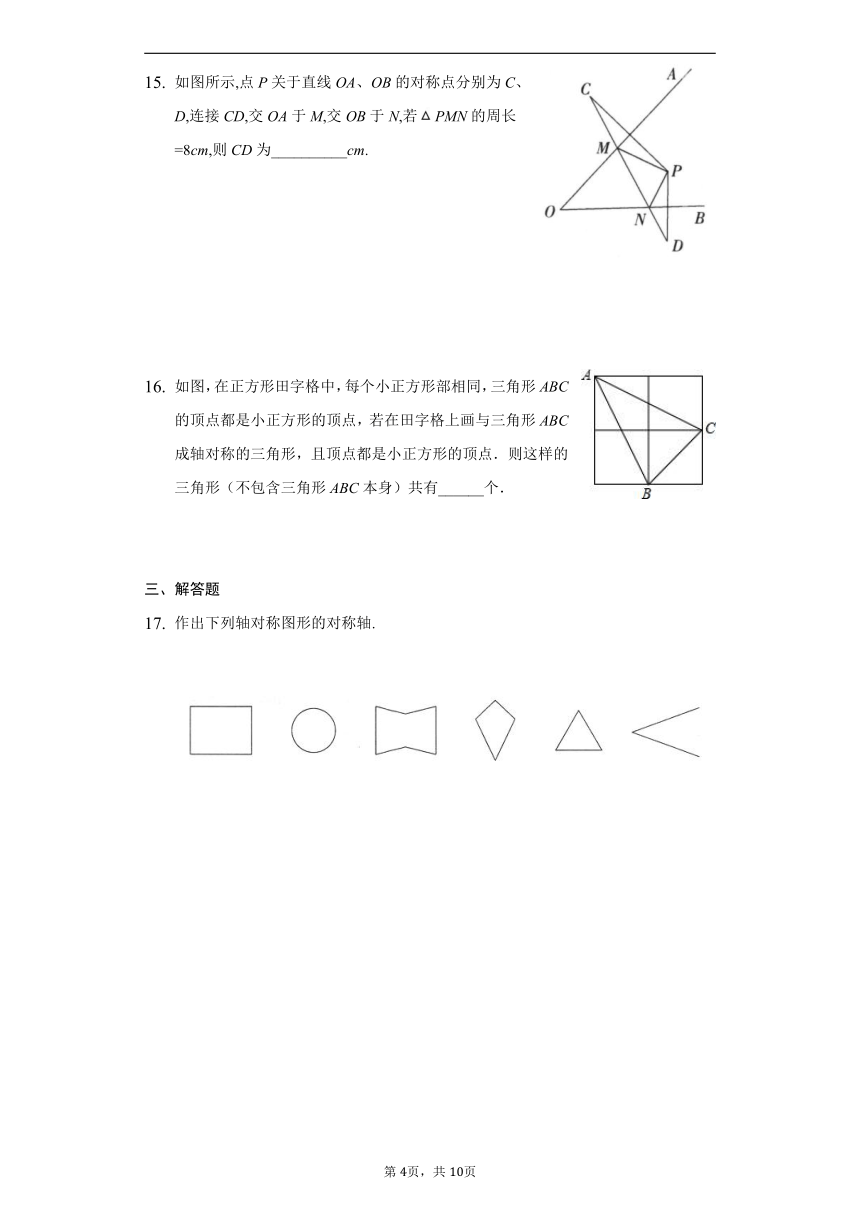
如图所示,点P关于直线OA、OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若PMN的周长=8cm,则CD为__________cm.
如图,在正方形田字格中,每个小正方形部相同,三角形ABC的顶点都是小正方形的顶点,若在田字格上画与三角形ABC成轴对称的三角形,且顶点都是小正方形的顶点.则这样的三角形(不包含三角形ABC本身)共有______个.
三、解答题
作出下列轴对称图形的对称轴.
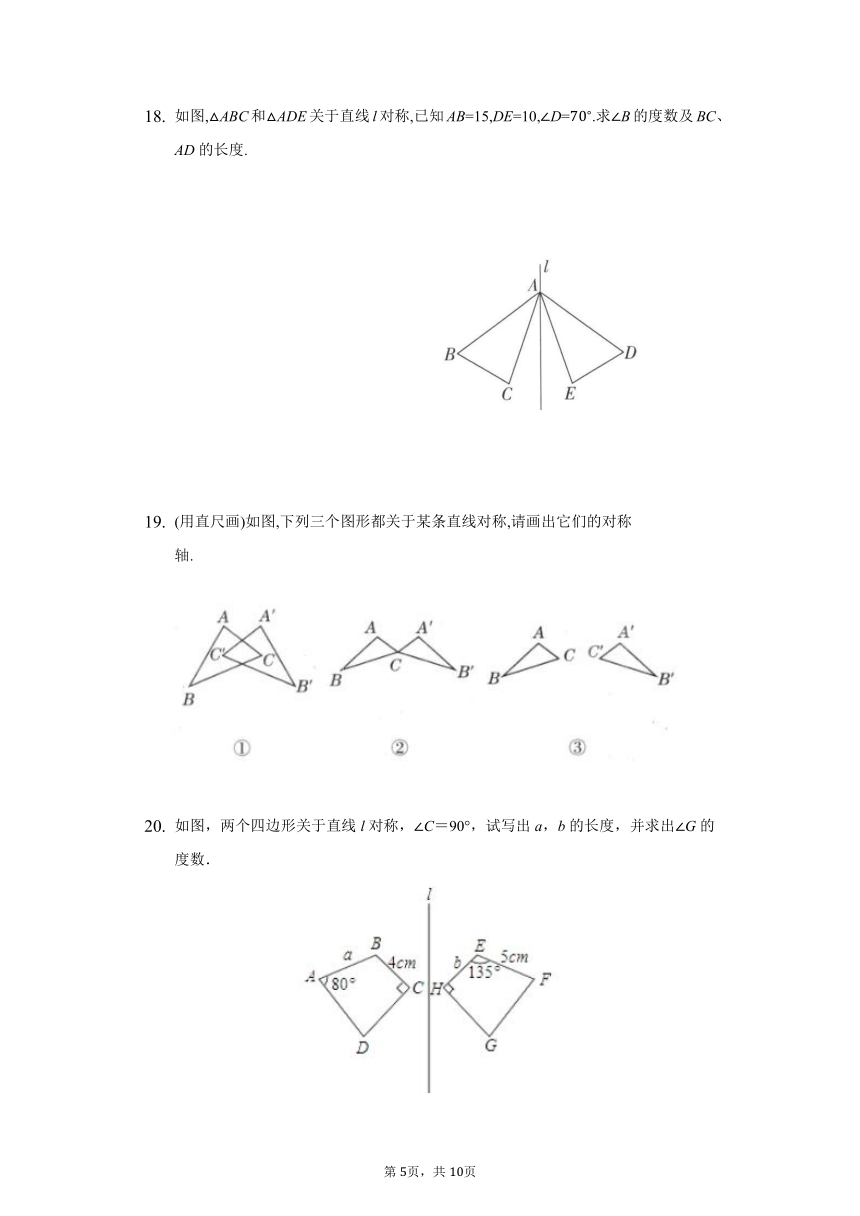
如图,ABC和ADE关于直线l对称,已知AB=15,DE=10,D=.求B的度数及BC、AD的长度.
(用直尺画)如图,下列三个图形都关于某条直线对称,请画出它们的对称轴.
如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
如图,点P在AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN分别交OA,OB于点E,F.
(1)若MN=20cm,求PEF的周长;
(2)若AOB=,求EPF的度数.
如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
参考答案
1.D
2.B
3.D
4.D
5.C
6.D
7.D
8.B
9.10°
10. 5
11.AN625
12.24
13.160°
14.130°
15.8
16.3
17.
18.解:ABC和ADE关于直线l对称,
AB=AD,BC=DE,B=D.
又AB=15,DE=10,D=,
B=,BC=10,AD=15.
19.解:如图所示.
20.解:∵两个四边形关于直线l对称,
∴四边形ABCD与四边形FEHG可以完全重合,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5cm,b=4cm,
∴∠G=360°-∠H-∠E-∠F=55°.
21.解:(1)点M,N分别是点P关于直线OA,OB的对称点,
ME=PE,NF=PF.
PE+EF+PF=ME+EF+NF=MN=20cm,
即PEF的周长是20cm.
(2)如图,设MP与OA相交于点R,PN与OB相交于点T.
由(1)知ME=PE,NF=PF,
M=EPM,N=FPN.
PEF=2M,PFE=2N.
PRE=PTF=,
在四边形OTPR中,MPN+AOB=.
MPN+M+N=,
M+N=AOB=.
EPF=-(PEF+PFE)=-2(M+N)=-2=.
22.解:QR=4.5cm,理由如下:
∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
∴PM=MQ,PN=NR.
∵PM=2.5cm,PN=3cm,MN=4cm,
∴RN=3cm,MQ=2.5cm,NQ=MN-MQ=4-2.5=1.5(cm).
∴QR=RN+NQ=3+1.5=4.5(cm).
第6页,共10页
第7页,共10页
13.1.1轴对称练习题
一、选择题
如图所示的4组图形中,成轴对称的有( )
A. 4组 B. 3组 C. 2组 D. 1组
如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A. 2条
B. 4条
C. 6条
D. 8条
在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为( )
A. B. C. D.
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.
B.
C.
D.
如图,A=,C'=,ABC与A'B'C'关于直线l对称,则B的度数为( )
A. B. C. D.
小华在镜子中看到身后墙上的钟,你认为时间最接近8时整的是( )
A. B.
C. D.
如图,ABC中,D点在BC上,将D点分别以AB、AC所在直线为对称轴,画出对称点E、F,并连接AE、AF,根据图中标示的角度,可得EAF的度数为( )
A. B. C. D.
如图,在四边形ABCD中,边AB与AD关于AC对称,则下列结论正确的是( )
CA平分BCD;AC平分BAD;BDAC;BD平分AC.
A. B. C. D.
二、填空题
如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为______.
如图,在ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若ABC的面积为,则图中阴影部分的面积是 .
如图,从汽车的后视镜中看见某车牌的5位号码的车牌号为____________.
如图,四边形ABCD的对称轴是AD所在的直线,AC=5,DB=7,则四边形ABCD的周长为______.
如图,是一个风筝的图案,它是轴对称图形,EF是对称轴,∠A=90°,∠AED=120°,∠C=50°,则∠BFC的度数为____.
如图是小明制作的风筝,为了平衡做成了轴对称图形.已知OC所在直线是对称轴,A=,BCO=,那么AOB=__________.
如图所示,点P关于直线OA、OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若PMN的周长=8cm,则CD为__________cm.
如图,在正方形田字格中,每个小正方形部相同,三角形ABC的顶点都是小正方形的顶点,若在田字格上画与三角形ABC成轴对称的三角形,且顶点都是小正方形的顶点.则这样的三角形(不包含三角形ABC本身)共有______个.
三、解答题
作出下列轴对称图形的对称轴.
如图,ABC和ADE关于直线l对称,已知AB=15,DE=10,D=.求B的度数及BC、AD的长度.
(用直尺画)如图,下列三个图形都关于某条直线对称,请画出它们的对称轴.
如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
如图,点P在AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN分别交OA,OB于点E,F.
(1)若MN=20cm,求PEF的周长;
(2)若AOB=,求EPF的度数.
如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为多少.
参考答案
1.D
2.B
3.D
4.D
5.C
6.D
7.D
8.B
9.10°
10. 5
11.AN625
12.24
13.160°
14.130°
15.8
16.3
17.
18.解:ABC和ADE关于直线l对称,
AB=AD,BC=DE,B=D.
又AB=15,DE=10,D=,
B=,BC=10,AD=15.
19.解:如图所示.
20.解:∵两个四边形关于直线l对称,
∴四边形ABCD与四边形FEHG可以完全重合,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5cm,b=4cm,
∴∠G=360°-∠H-∠E-∠F=55°.
21.解:(1)点M,N分别是点P关于直线OA,OB的对称点,
ME=PE,NF=PF.
PE+EF+PF=ME+EF+NF=MN=20cm,
即PEF的周长是20cm.
(2)如图,设MP与OA相交于点R,PN与OB相交于点T.
由(1)知ME=PE,NF=PF,
M=EPM,N=FPN.
PEF=2M,PFE=2N.
PRE=PTF=,
在四边形OTPR中,MPN+AOB=.
MPN+M+N=,
M+N=AOB=.
EPF=-(PEF+PFE)=-2(M+N)=-2=.
22.解:QR=4.5cm,理由如下:
∵点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
∴PM=MQ,PN=NR.
∵PM=2.5cm,PN=3cm,MN=4cm,
∴RN=3cm,MQ=2.5cm,NQ=MN-MQ=4-2.5=1.5(cm).
∴QR=RN+NQ=3+1.5=4.5(cm).
第6页,共10页
第7页,共10页
