13.1.2线段的垂直平分线的性质练习题(人教版数学八年级上期)(word版含答案)
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质练习题(人教版数学八年级上期)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 08:41:04 | ||
图片预览


文档简介
人教版数学八年级上期
13.1.2线段的垂直平分线的性质练习题
一、选择题
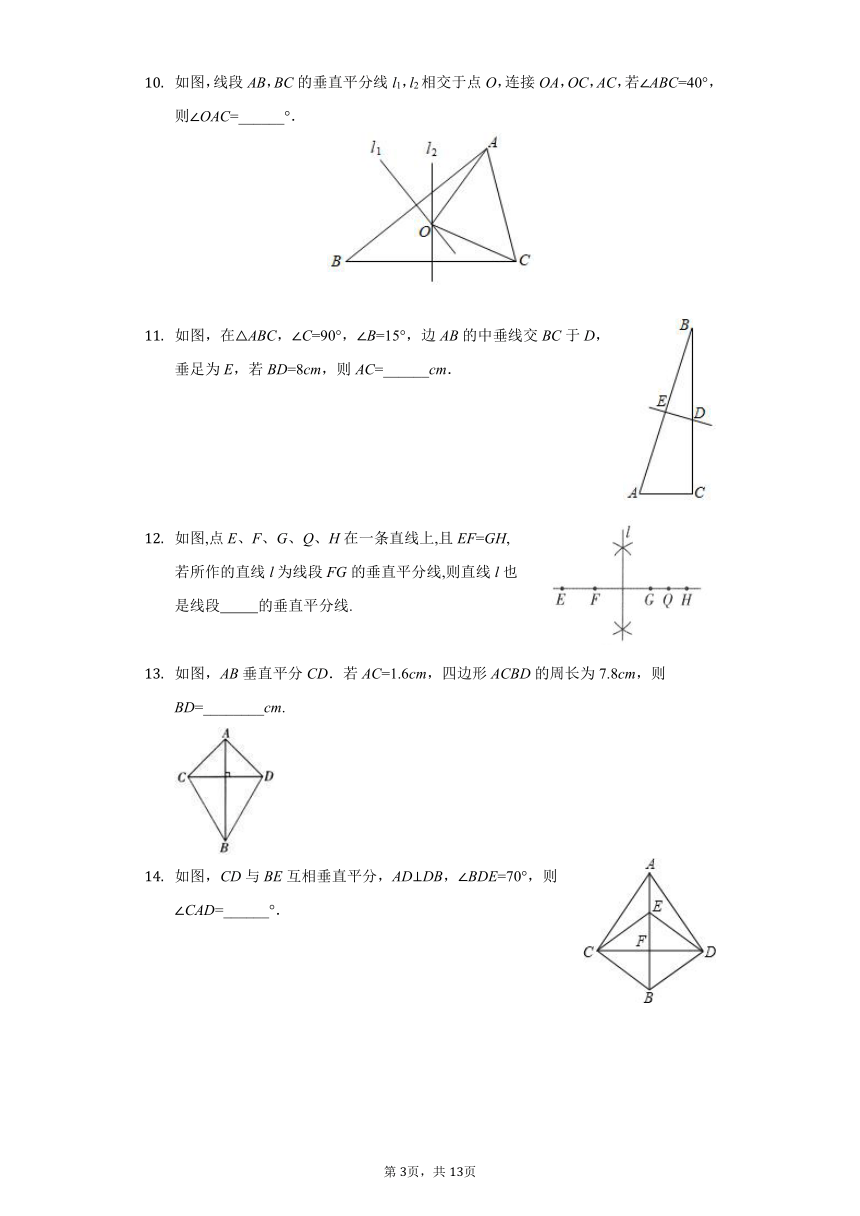
如图,CD是线段AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( )
A.
B.
C. 4cm
D.
如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A. l是线段EH的垂直平分线
B. l是线段EQ的垂直平分线
C. l是线段FH的垂直平分线
D. EH是l的垂直平分线
如图,AC=AD,BC=BD,则有( )
A. AB垂直平分CD
B. CD垂直平分AB
C. AB与CD互相垂直平分
D. 以上都不正确
如图所示的尺规作图的痕迹表示的是( )
A. 尺规作线段的垂直平分线
B. 尺规作一条线段等于已知线段
C. 尺规作一个角等于已知角
D. 尺规作角的平分线
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
A. 4cm
B. 3 cm
C. 2cm
D. 1cm
在锐角ABC内一点P满足PA=PB=PC,则点P是ABC( )
A. 三条角平分线的交点 B. 三条中线的交点
C. 三条高的交点 D. 三边垂直平分线的交点
如图,在△ABC中,边AB的垂直平分线分别交AB,BC于D,E,边AC的垂直平分线分别交AC,BC于F,G,若△AEG的周长为8,则BC长是( )
A. 12 B. 8 C. 6 D. 4
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A. 1 B. 2 C. 3 D. 4
二、填空题
如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为________.
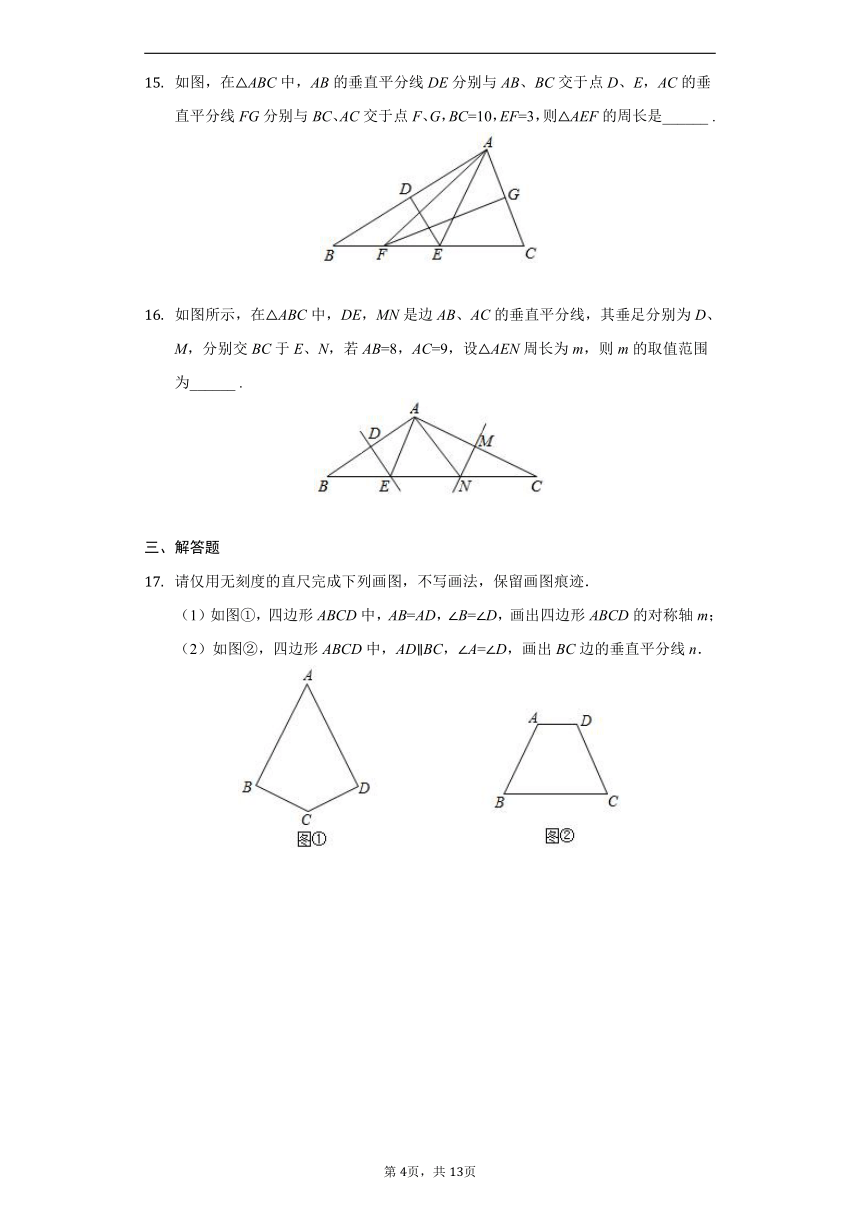
如图,线段AB,BC的垂直平分线l1,l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠OAC=______°.
如图,在△ABC,∠C=90°,∠B=15°,边AB的中垂线交BC于D,垂足为E,若BD=8cm,则AC=______cm.
如图,点E、F、G、Q、H在一条直线上,且EF=GH,若所作的直线l为线段FG的垂直平分线,则直线l也是线段 的垂直平分线.
如图,AB垂直平分CD.若AC=1.6cm,四边形ACBD的周长为7.8cm,则BD=________cm.
如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
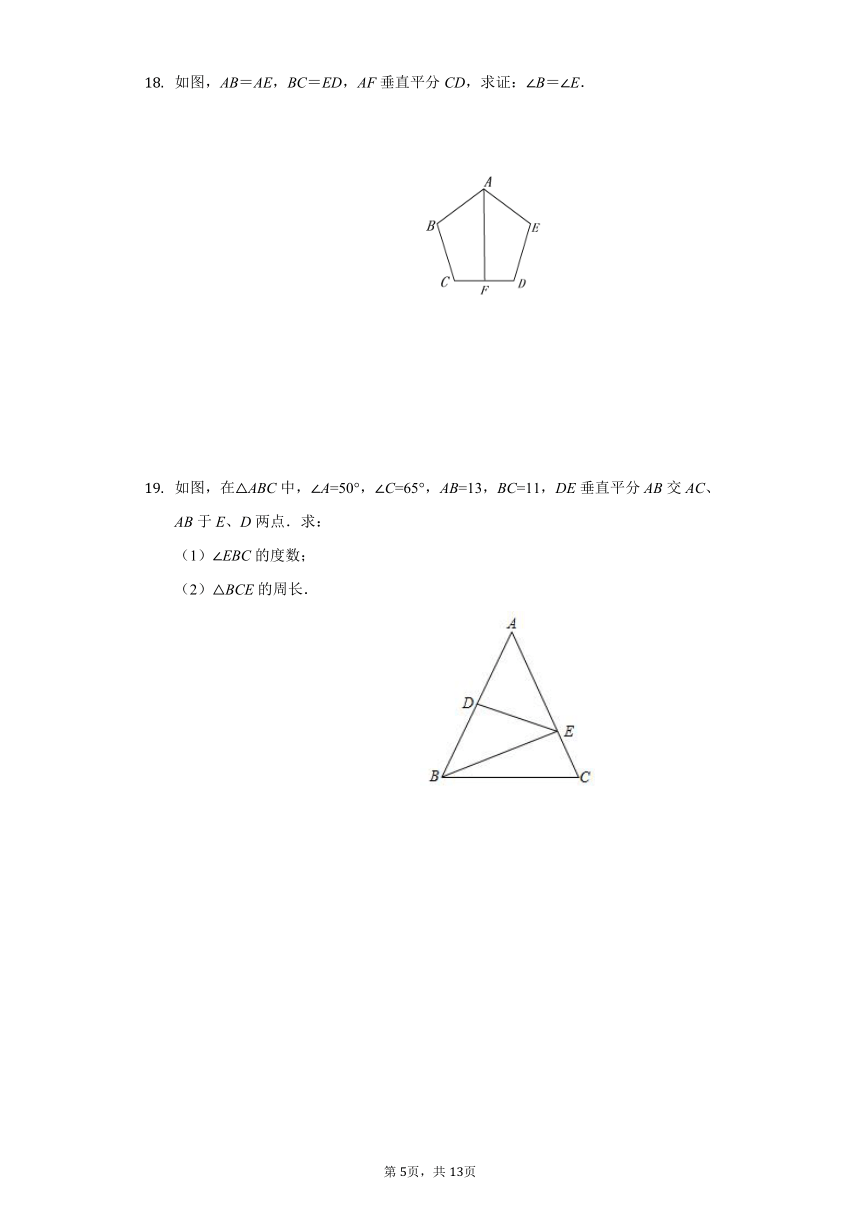
如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是______ .
如图所示,在△ABC中,DE,MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为______ .
三、解答题
请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
如图,AB=AE,BC=ED,AF垂直平分CD,求证:∠B=∠E.
如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
(1)如图(1),AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,求∠DBC的度数;
(2)如图(2),△ABC中,AB=AC,AD和BE是两条高,交于点H,且AE=BE,求证:AH=2BD.
如图,在△ABC中,∠ACB=90°,D是BC的延长线上一点,EH是BD的垂直平分线,DE交AC于F,求证:E在AF的垂直平分线上.
已知:如图,AC与DE相交于点O,AB=DF,BE=CF,∠B=∠F.求证:点O在线段EC的垂直平分线上.
如图,AD是的角平分线,DE、DF分别是和的高.
求证:;垂直平分EF.
如图,△ABC中,AC>AB,AE为外角∠FAC的平分线,同时点E也在BC的垂直平分线上,若AB=AE,试判断∠ABC与∠ACB的数量关系,并加以证明.
参考答案
1.B
2.A
3.A
4.A
5.B
6.D
7.B
8.C
9.30°
10.50
11.4
12.EH
13.2.3
14.70
15.16
16.<m<17
17.解:(1)如图①,直线m即为所求
(2)如图②,直线n即为所求
18.证明:连接AC,AD,
∵AF是CD的垂直平分线,
∴AC=AD.
又AB=AE,BC=ED,
∴△ABC≌△AED(SSS).
∴∠B=∠E.
19.解:(1)在△ABC中,∠A=50°,∠C=65°,
则∠ABC=180°-∠A-∠C=65°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=50°,
∴∠EBC=∠ABC-∠ABE=15°;
(2)∵∠ABC=∠C=65°,
∴AC=AB=13,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=24.
20.(1)解:∵△ABC中,AB=AC,∠A=50°,
∴∠ABC=∠C=(180°-∠A)=65°,
∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°;
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2BD,
∵BE⊥AC,AD⊥BC,
∴∠ADB=∠BEC=∠AEH=90°,
∵∠CBE+∠BHD+∠ADB=180°,∠AEH+∠EAH+∠AHE=180°,∠AHE=∠BHD,
∴∠EAH=∠CBE,
在△AEH和△BEC中,,
∴△AEH≌△BEC(ASA),
∴AH=BC,
∵BC=2BD,
∴AH=2BD.
21.证明:∵EH垂直平分BD,
∴BE=DE,
∴∠BEH=∠DEH,
∵∠ACB=90°,
∴EH∥AC,
∴∠BEH=∠BAC,∠DEH=∠AFE,
∴∠EAF=∠AFE,
∴AE=EF,
∴点E在AF的垂直平分线上.
22.证明:∵BE=CF,
∴BE+EC=CF+CE,
即BC=FE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS),
∴∠ACB=∠DEF,
∴OE=OC,
∴点O在线段EC的垂直平分线上.
23.证明:(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴∠DEF=∠DFE;
(2)在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
而DE=DF,
∴AD垂直平分EF.
24.∠ABC=3∠ACB,
证明:
过E作EM⊥BA于M,EN⊥AC于N,
则∠EMB=∠ENC=90°,
∵AE平分∠MAC,
∴EM=EN,
∵E在BC的垂直平分线上,
∴BE=CE,
在Rt△BME和Rt△CNE中
∴Rt△BME≌Rt△CNE(HL),
∴∠ABE=∠ECA,
∴A、B、C、E四点共圆,
∴∠ACB=∠AEB,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=∠ACB=∠ACE,
∵BE=CE,
∵∠EBC=∠ECB,
∴∠ABC=∠ABE+∠EBC
=∠ACB+∠ECB
=∠ACB+∠ACB+∠ECA
=∠ACB+∠ACB+∠ACB
=3∠ACB.
第8页,共13页
第9页,共13页
13.1.2线段的垂直平分线的性质练习题
一、选择题
如图,CD是线段AB的垂直平分线,若AC=1.6cm,BD=2.3cm,则四边形ABCD的周长是( )
A.
B.
C. 4cm
D.
如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A. l是线段EH的垂直平分线
B. l是线段EQ的垂直平分线
C. l是线段FH的垂直平分线
D. EH是l的垂直平分线
如图,AC=AD,BC=BD,则有( )
A. AB垂直平分CD
B. CD垂直平分AB
C. AB与CD互相垂直平分
D. 以上都不正确
如图所示的尺规作图的痕迹表示的是( )
A. 尺规作线段的垂直平分线
B. 尺规作一条线段等于已知线段
C. 尺规作一个角等于已知角
D. 尺规作角的平分线
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为( )
A. 4cm
B. 3 cm
C. 2cm
D. 1cm
在锐角ABC内一点P满足PA=PB=PC,则点P是ABC( )
A. 三条角平分线的交点 B. 三条中线的交点
C. 三条高的交点 D. 三边垂直平分线的交点
如图,在△ABC中,边AB的垂直平分线分别交AB,BC于D,E,边AC的垂直平分线分别交AC,BC于F,G,若△AEG的周长为8,则BC长是( )
A. 12 B. 8 C. 6 D. 4
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A. 1 B. 2 C. 3 D. 4
二、填空题
如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为________.
如图,线段AB,BC的垂直平分线l1,l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠OAC=______°.
如图,在△ABC,∠C=90°,∠B=15°,边AB的中垂线交BC于D,垂足为E,若BD=8cm,则AC=______cm.
如图,点E、F、G、Q、H在一条直线上,且EF=GH,若所作的直线l为线段FG的垂直平分线,则直线l也是线段 的垂直平分线.
如图,AB垂直平分CD.若AC=1.6cm,四边形ACBD的周长为7.8cm,则BD=________cm.
如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是______ .
如图所示,在△ABC中,DE,MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,若AB=8,AC=9,设△AEN周长为m,则m的取值范围为______ .
三、解答题
请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
如图,AB=AE,BC=ED,AF垂直平分CD,求证:∠B=∠E.
如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
(1)如图(1),AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,求∠DBC的度数;
(2)如图(2),△ABC中,AB=AC,AD和BE是两条高,交于点H,且AE=BE,求证:AH=2BD.
如图,在△ABC中,∠ACB=90°,D是BC的延长线上一点,EH是BD的垂直平分线,DE交AC于F,求证:E在AF的垂直平分线上.
已知:如图,AC与DE相交于点O,AB=DF,BE=CF,∠B=∠F.求证:点O在线段EC的垂直平分线上.
如图,AD是的角平分线,DE、DF分别是和的高.
求证:;垂直平分EF.
如图,△ABC中,AC>AB,AE为外角∠FAC的平分线,同时点E也在BC的垂直平分线上,若AB=AE,试判断∠ABC与∠ACB的数量关系,并加以证明.
参考答案
1.B
2.A
3.A
4.A
5.B
6.D
7.B
8.C
9.30°
10.50
11.4
12.EH
13.2.3
14.70
15.16
16.<m<17
17.解:(1)如图①,直线m即为所求
(2)如图②,直线n即为所求
18.证明:连接AC,AD,
∵AF是CD的垂直平分线,
∴AC=AD.
又AB=AE,BC=ED,
∴△ABC≌△AED(SSS).
∴∠B=∠E.
19.解:(1)在△ABC中,∠A=50°,∠C=65°,
则∠ABC=180°-∠A-∠C=65°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=50°,
∴∠EBC=∠ABC-∠ABE=15°;
(2)∵∠ABC=∠C=65°,
∴AC=AB=13,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=24.
20.(1)解:∵△ABC中,AB=AC,∠A=50°,
∴∠ABC=∠C=(180°-∠A)=65°,
∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°;
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2BD,
∵BE⊥AC,AD⊥BC,
∴∠ADB=∠BEC=∠AEH=90°,
∵∠CBE+∠BHD+∠ADB=180°,∠AEH+∠EAH+∠AHE=180°,∠AHE=∠BHD,
∴∠EAH=∠CBE,
在△AEH和△BEC中,,
∴△AEH≌△BEC(ASA),
∴AH=BC,
∵BC=2BD,
∴AH=2BD.
21.证明:∵EH垂直平分BD,
∴BE=DE,
∴∠BEH=∠DEH,
∵∠ACB=90°,
∴EH∥AC,
∴∠BEH=∠BAC,∠DEH=∠AFE,
∴∠EAF=∠AFE,
∴AE=EF,
∴点E在AF的垂直平分线上.
22.证明:∵BE=CF,
∴BE+EC=CF+CE,
即BC=FE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS),
∴∠ACB=∠DEF,
∴OE=OC,
∴点O在线段EC的垂直平分线上.
23.证明:(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴∠DEF=∠DFE;
(2)在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
而DE=DF,
∴AD垂直平分EF.
24.∠ABC=3∠ACB,
证明:
过E作EM⊥BA于M,EN⊥AC于N,
则∠EMB=∠ENC=90°,
∵AE平分∠MAC,
∴EM=EN,
∵E在BC的垂直平分线上,
∴BE=CE,
在Rt△BME和Rt△CNE中
∴Rt△BME≌Rt△CNE(HL),
∴∠ABE=∠ECA,
∴A、B、C、E四点共圆,
∴∠ACB=∠AEB,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=∠ACB=∠ACE,
∵BE=CE,
∵∠EBC=∠ECB,
∴∠ABC=∠ABE+∠EBC
=∠ACB+∠ECB
=∠ACB+∠ACB+∠ECA
=∠ACB+∠ACB+∠ACB
=3∠ACB.
第8页,共13页
第9页,共13页
