3.4.1.5 相似三角形的判定综合练习 (含答案)
文档属性
| 名称 | 3.4.1.5 相似三角形的判定综合练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 20:43:08 | ||
图片预览



文档简介
3.4 相似三角形的判定与性质
3.4.1 相似三角形的判定
第5课时 相似三角形的判定综合练习
一、选择题
1.【2021·贵港】下列命题是真命题的是( )
A.同旁内角相等,两直线平行
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.两角分别相等的两个三角形相似
2.下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
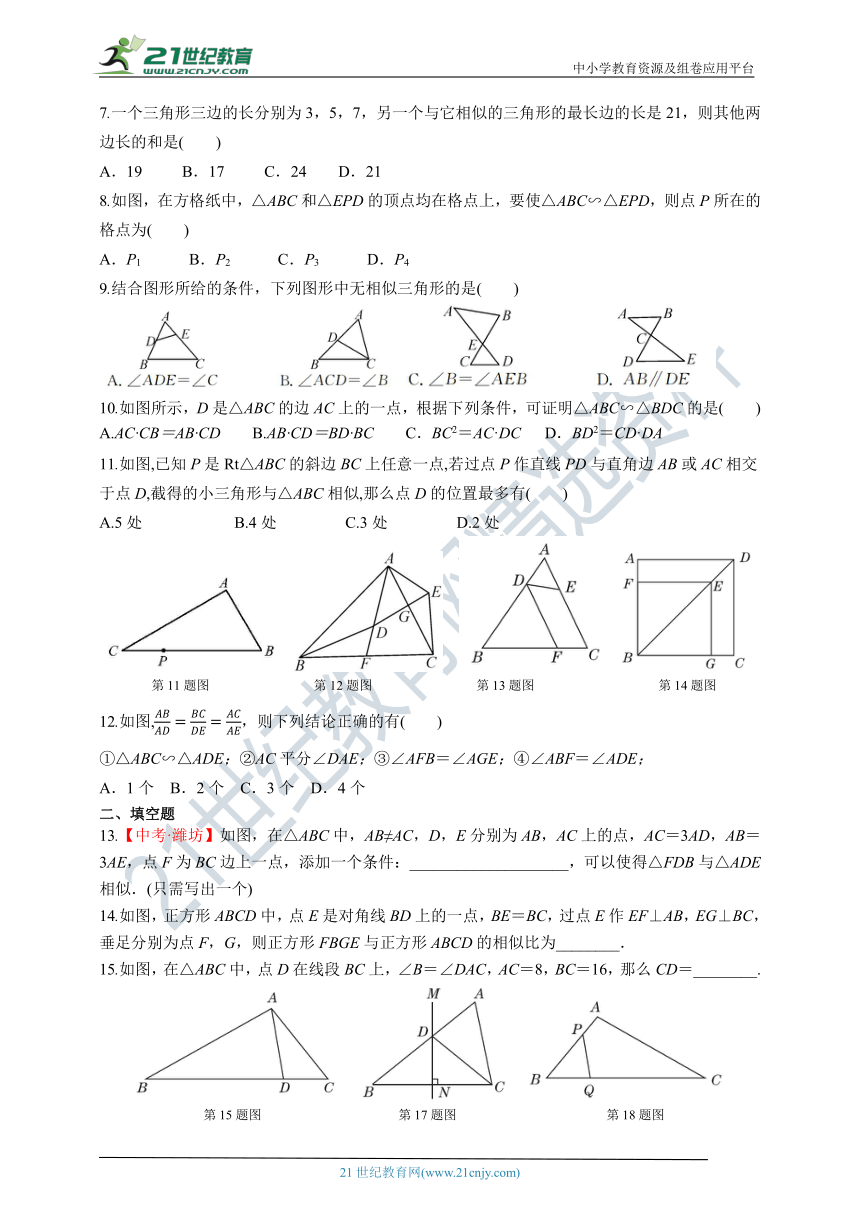
3.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10 B.12 C. D.
第3题图 第6题图 第8题图 第10题图
4.六边形ABCDEF与六边形A′B′C′D′E′F′相似,若对应边AB与A′B′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F′与六边形ABCDEF的相似比是( )
A.5:4 B.4:5 C.5:2 D.2:
5.【2019·雅安】如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
6.【2021·衡水至臻中学校级月考】如图,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AD、宽为AC的矩形面积,AB=AD,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
7.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19 B.17 C.24 D.21
8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1 B.P2 C.P3 D.P4
9.结合图形所给的条件,下列图形中无相似三角形的是( )
10.如图所示,D是△ABC的边AC上的一点,根据下列条件,可证明△ABC∽△BDC的是( )
A.AC·CB=AB·CD B.AB·CD=BD·BC C.BC2=AC·DC D.BD2=CD·DA
11.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么点D的位置最多有( )
A.5处 B.4处 C.3处 D.2处
第11题图 第12题图 第13题图 第14题图
12.如图,,则下列结论正确的有( )
①△ABC∽△ADE;②AC平分∠DAE;③∠AFB=∠AGE;④∠ABF=∠ADE;
A.1个 B.2个 C.3个 D.4个
二、填空题
13.【中考·潍坊】如图,在△ABC中,AB≠AC,D,E分别为AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:____________________,可以使得△FDB与△ADE相似.(只需写出一个)
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为________.
15.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD=________.
第15题图 第17题图 第18题图
16.已知锐角三角形ABC中,AB=9,AC=6,D为AB上的一个点,AD=3,在AC上找一点E,使△ADE与△ABC相似,则AE=________.
17.【2021·衡水市第五中学校级月考】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
18.如图,在△ABC中,AB=10 cm,BC=20 cm,点P从点A开始沿AB边向点B以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,问经过________s时,△PBQ与△ABC相似.
三、解答题
19.【2019·张家界】如图,在平行四边形ABCD中,连结对角线AC,延长AB至点E,使BE=AB,连结DE,分别交BC,AC于点F,G.
(1)求证:BF=CF.
(2)若BC=6,DG=4,求FG的长.
20.已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB·AC=AD·AE.求证:△BEF∽△ACF.
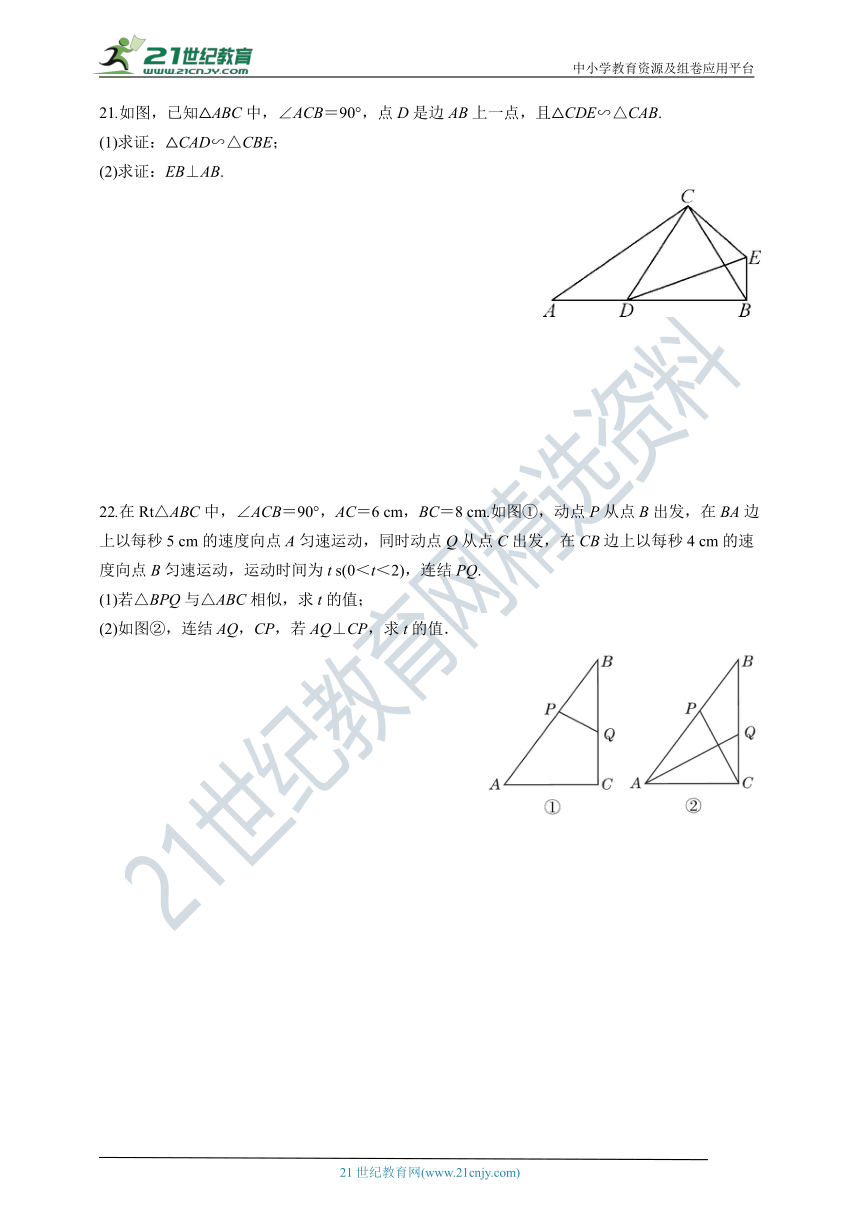
21.如图,已知△ABC中,∠ACB=90°,点D是边AB上一点,且△CDE∽△CAB.
(1)求证:△CAD∽△CBE;
(2)求证:EB⊥AB.
22.在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.如图①,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t s(0<t<2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)如图②,连结AQ,CP,若AQ⊥CP,求t的值.
23.如图,在等腰△ABC中,AB=AC,点M,N分别是BC,AC边上的点(M,N不与点B,C重合),且∠1=∠B.
(1)求证:∠BAM=∠CMN.
(2)若AB=5,BC=8,
①当BM=时,MN与AB是否平行 若平行,请证明;若不平行,请说明理由.
②当△AMN为等腰三角形时,求BM的长.
24.如图1,在四边形ABCD中,E,F分别是AB,CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD,BC所在直线互相垂直,求的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2021·贵港】下列命题是真命题的是( D )
A.同旁内角相等,两直线平行 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.两角分别相等的两个三角形相似
2.下列四组图形中,一定相似的是( D )
A.正方形与矩形 B.正方形与菱形
C.菱形与菱形 D.正五边形与正五边形
3.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( C )
A.10 B.12 C. D.
第3题图 第6题图 第8题图 第10题图
4.六边形ABCDEF与六边形A′B′C′D′E′F′相似,若对应边AB与A′B′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F′与六边形ABCDEF的相似比是( B )
A.5:4 B.4:5 C.5:2 D.2:
5.【2019·雅安】如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( B )
6.【2021·衡水至臻中学校级月考】如图,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AD、宽为AC的矩形面积,AB=AD,则S1与S2的大小关系为( B )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
7.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( C )
A.19 B.17 C.24 D.21
8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( C )
A.P1 B.P2 C.P3 D.P4
9.结合图形所给的条件,下列图形中无相似三角形的是( C )
10.如图所示,D是△ABC的边AC上的一点,根据下列条件,可证明△ABC∽△BDC的是( C )
A.AC·CB=AB·CD B.AB·CD=BD·BC C.BC2=AC·DC D.BD2=CD·DA
11.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么点D的位置最多有( C )
A.5处 B.4处 C.3处 D.2处
第11题图 第12题图 第13题图 第14题图
12.如图,,则下列结论正确的有( B )
①△ABC∽△ADE;②AC平分∠DAE;③∠AFB=∠AGE;④∠ABF=∠ADE;
A.1个 B.2个 C.3个 D.4个
【提示】①④正确
二、填空题
13.【中考·潍坊】如图,在△ABC中,AB≠AC,D,E分别为AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:____________________,可以使得△FDB与△ADE相似.(只需写出一个)
【答案】DF∥AC(答案不唯一)
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为________.
【答案】
15.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD=________.
【答案】4
第15题图 第17题图 第18题图
16.已知锐角三角形ABC中,AB=9,AC=6,D为AB上的一个点,AD=3,在AC上找一点E,使△ADE与△ABC相似,则AE=________.
【答案】2或4.5
17.【2021·衡水市第五中学校级月考】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
【答案】
18.如图,在△ABC中,AB=10 cm,BC=20 cm,点P从点A开始沿AB边向点B以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,问经过________s时,△PBQ与△ABC相似.
【答案】1或2.5
三、解答题
19.【2019·张家界】如图,在平行四边形ABCD中,连结对角线AC,延长AB至点E,使BE=AB,连结DE,分别交BC,AC于点F,G.
(1)求证:BF=CF.
证明:∵BE=AB,∴=.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.∴∠EBF=∠EAD.
又∵∠BEF=∠AED,∴△EBF∽△EAD.
∴==.∴BF=AD=BC.∴BF=CF.
(2)若BC=6,DG=4,求FG的长.
解:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠FCG=∠DAG.
又∵∠FGC=∠DGA,
∴△FGC∽△DGA.
∴=,即=,解得FG=2.
20.已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB·AC=AD·AE.求证:△BEF∽△ACF.
证明:∵AD是△ABC的高,∴∠ADC=90°.
∵BE⊥AB,∴∠EBA=90°,
∴∠ADC=∠EBA=90°.
∵AB·AC=AD·AE,∴AB∶AD=AE∶AC.
设AB∶AD=AE∶AC=k(k≠0),
根据勾股定理,
得BE===kCD,
∴=k,∴=.
又∵∠ABE=∠ADC,∴△ABE∽△ADC,
∴∠E=∠C.
∵∠BFE=∠AFC,∴△BEF∽△ACF.
21.如图,已知△ABC中,∠ACB=90°,点D是边AB上一点,且△CDE∽△CAB.
(1)求证:△CAD∽△CBE;
(2)求证:EB⊥AB.
证明:(1)∵△CDE∽△CAB,
∴=,∠ACB=∠DCE,∴=,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE,
∴△CAD∽△CBE.
(2)∵△CAD∽△CBE,
∴∠CAD=∠CBE.
∵∠ACB=90°,
∴∠CAD+∠CBA=90°,
∴∠CBE+∠CBA=90°,
∴EB⊥AB.
22.在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.如图①,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t s(0<t<2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
解:由题意知,AB=10 cm,BP=5t cm,CQ=4t cm. BQ=(8-4t)cm.
当△PBQ∽△ABC时,有=,即=.解得t=1.
当△QBP∽△ABC时,有=,即=,解得t=.
∴当△BPQ与△ABC相似时,t=1或t=.
(2)如图②,连结AQ,CP,若AQ⊥CP,求t的值.
解:过点P作PM⊥BC于点M,则PM∥AC,设AQ,CP交于点N,如图所示.
易知△BMP∽△BCA,∴==,
∴==.∴PM=3t cm,BM=4t cm,
则CM=(8-4t)cm.
∵AQ⊥PC,∴∠ANC=90°,∴∠QAC+∠NCA=90°,
又∵∠PCM+∠NCA=90°,∴∠QAC=∠PCM.
又∵∠ACQ=∠PMC=90°,∴△ACQ∽△CMP,
∴=,∴=,解得t=.
23.如图,在等腰△ABC中,AB=AC,点M,N分别是BC,AC边上的点(M,N不与点B,C重合),且∠1=∠B.
(1)求证:∠BAM=∠CMN.
(2)若AB=5,BC=8,
①当BM=时,MN与AB是否平行 若平行,请证明;若不平行,请说明理由.
②当△AMN为等腰三角形时,求BM的长.
解:(1)∵∠1+∠CMN=∠B+∠BAM,∠1=∠B,
∴∠BAM=∠CMN.
(2)①MN∥AB.
理由:∵,∠B=∠B,
∴△ABM∽△CBA,∠BAM=∠C=∠1,∴MN∥AB.
②当AM=AN时,∠1=∠MNA,
∴点N与C重合,不合题意,应舍去;
当MA=MN时,△ABM≌△MCN,AB=MC=5,
∴BM=8-5=3;
当AN=MN时,∵△ABC∽△MCA,
∴,∴MC=,∴BM=.
综上所述,当△AMN是等腰三角形时,BM的长为3或.
24.如图1,在四边形ABCD中,E,F分别是AB,CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD,BC所在直线互相垂直,求的值.
解:(1)∵GE是AB的垂直平分线,
∴GA=GB,同理GD=GC.
在△AGD和△BGC中,∵GA=GB,∠AGD=∠BGC,GD=GC,
∴△AGD≌△BGC,∴AD=BC.
(2)∵∠AGD=∠BGC,∴∠AGB=∠DGC.
在△AGB和△DGC中,,∠AGB=∠DGC,
∴△AGB∽△DGC.
∴,∠AGE=∠DGF,
∴∠AGD=∠EGF,∴△AGD∽△EGF.
(3).
3.4.1 相似三角形的判定
第5课时 相似三角形的判定综合练习
一、选择题
1.【2021·贵港】下列命题是真命题的是( )
A.同旁内角相等,两直线平行
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.两角分别相等的两个三角形相似
2.下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
3.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( )
A.10 B.12 C. D.
第3题图 第6题图 第8题图 第10题图
4.六边形ABCDEF与六边形A′B′C′D′E′F′相似,若对应边AB与A′B′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F′与六边形ABCDEF的相似比是( )
A.5:4 B.4:5 C.5:2 D.2:
5.【2019·雅安】如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
6.【2021·衡水至臻中学校级月考】如图,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AD、宽为AC的矩形面积,AB=AD,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
7.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( )
A.19 B.17 C.24 D.21
8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1 B.P2 C.P3 D.P4
9.结合图形所给的条件,下列图形中无相似三角形的是( )
10.如图所示,D是△ABC的边AC上的一点,根据下列条件,可证明△ABC∽△BDC的是( )
A.AC·CB=AB·CD B.AB·CD=BD·BC C.BC2=AC·DC D.BD2=CD·DA
11.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么点D的位置最多有( )
A.5处 B.4处 C.3处 D.2处
第11题图 第12题图 第13题图 第14题图
12.如图,,则下列结论正确的有( )
①△ABC∽△ADE;②AC平分∠DAE;③∠AFB=∠AGE;④∠ABF=∠ADE;
A.1个 B.2个 C.3个 D.4个
二、填空题
13.【中考·潍坊】如图,在△ABC中,AB≠AC,D,E分别为AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:____________________,可以使得△FDB与△ADE相似.(只需写出一个)
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为________.
15.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD=________.
第15题图 第17题图 第18题图
16.已知锐角三角形ABC中,AB=9,AC=6,D为AB上的一个点,AD=3,在AC上找一点E,使△ADE与△ABC相似,则AE=________.
17.【2021·衡水市第五中学校级月考】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
18.如图,在△ABC中,AB=10 cm,BC=20 cm,点P从点A开始沿AB边向点B以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,问经过________s时,△PBQ与△ABC相似.
三、解答题
19.【2019·张家界】如图,在平行四边形ABCD中,连结对角线AC,延长AB至点E,使BE=AB,连结DE,分别交BC,AC于点F,G.
(1)求证:BF=CF.
(2)若BC=6,DG=4,求FG的长.
20.已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB·AC=AD·AE.求证:△BEF∽△ACF.
21.如图,已知△ABC中,∠ACB=90°,点D是边AB上一点,且△CDE∽△CAB.
(1)求证:△CAD∽△CBE;
(2)求证:EB⊥AB.
22.在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.如图①,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t s(0<t<2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)如图②,连结AQ,CP,若AQ⊥CP,求t的值.
23.如图,在等腰△ABC中,AB=AC,点M,N分别是BC,AC边上的点(M,N不与点B,C重合),且∠1=∠B.
(1)求证:∠BAM=∠CMN.
(2)若AB=5,BC=8,
①当BM=时,MN与AB是否平行 若平行,请证明;若不平行,请说明理由.
②当△AMN为等腰三角形时,求BM的长.
24.如图1,在四边形ABCD中,E,F分别是AB,CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD,BC所在直线互相垂直,求的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2021·贵港】下列命题是真命题的是( D )
A.同旁内角相等,两直线平行 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.两角分别相等的两个三角形相似
2.下列四组图形中,一定相似的是( D )
A.正方形与矩形 B.正方形与菱形
C.菱形与菱形 D.正五边形与正五边形
3.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则C1D1的长是( C )
A.10 B.12 C. D.
第3题图 第6题图 第8题图 第10题图
4.六边形ABCDEF与六边形A′B′C′D′E′F′相似,若对应边AB与A′B′的长分别为50 cm和40 cm,则六边形A′B′C′D′E′F′与六边形ABCDEF的相似比是( B )
A.5:4 B.4:5 C.5:2 D.2:
5.【2019·雅安】如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( B )
6.【2021·衡水至臻中学校级月考】如图,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AD、宽为AC的矩形面积,AB=AD,则S1与S2的大小关系为( B )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
7.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边的长是21,则其他两边长的和是( C )
A.19 B.17 C.24 D.21
8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( C )
A.P1 B.P2 C.P3 D.P4
9.结合图形所给的条件,下列图形中无相似三角形的是( C )
10.如图所示,D是△ABC的边AC上的一点,根据下列条件,可证明△ABC∽△BDC的是( C )
A.AC·CB=AB·CD B.AB·CD=BD·BC C.BC2=AC·DC D.BD2=CD·DA
11.如图,已知P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么点D的位置最多有( C )
A.5处 B.4处 C.3处 D.2处
第11题图 第12题图 第13题图 第14题图
12.如图,,则下列结论正确的有( B )
①△ABC∽△ADE;②AC平分∠DAE;③∠AFB=∠AGE;④∠ABF=∠ADE;
A.1个 B.2个 C.3个 D.4个
【提示】①④正确
二、填空题
13.【中考·潍坊】如图,在△ABC中,AB≠AC,D,E分别为AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:____________________,可以使得△FDB与△ADE相似.(只需写出一个)
【答案】DF∥AC(答案不唯一)
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为________.
【答案】
15.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD=________.
【答案】4
第15题图 第17题图 第18题图
16.已知锐角三角形ABC中,AB=9,AC=6,D为AB上的一个点,AD=3,在AC上找一点E,使△ADE与△ABC相似,则AE=________.
【答案】2或4.5
17.【2021·衡水市第五中学校级月考】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为________.
【答案】
18.如图,在△ABC中,AB=10 cm,BC=20 cm,点P从点A开始沿AB边向点B以2 cm/s的速度移动,点Q从点B开始沿BC边向点C以4 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,问经过________s时,△PBQ与△ABC相似.
【答案】1或2.5
三、解答题
19.【2019·张家界】如图,在平行四边形ABCD中,连结对角线AC,延长AB至点E,使BE=AB,连结DE,分别交BC,AC于点F,G.
(1)求证:BF=CF.
证明:∵BE=AB,∴=.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.∴∠EBF=∠EAD.
又∵∠BEF=∠AED,∴△EBF∽△EAD.
∴==.∴BF=AD=BC.∴BF=CF.
(2)若BC=6,DG=4,求FG的长.
解:∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠FCG=∠DAG.
又∵∠FGC=∠DGA,
∴△FGC∽△DGA.
∴=,即=,解得FG=2.
20.已知:如图,AD是△ABC的高,BE⊥AB,AE交BC于点F,AB·AC=AD·AE.求证:△BEF∽△ACF.
证明:∵AD是△ABC的高,∴∠ADC=90°.
∵BE⊥AB,∴∠EBA=90°,
∴∠ADC=∠EBA=90°.
∵AB·AC=AD·AE,∴AB∶AD=AE∶AC.
设AB∶AD=AE∶AC=k(k≠0),
根据勾股定理,
得BE===kCD,
∴=k,∴=.
又∵∠ABE=∠ADC,∴△ABE∽△ADC,
∴∠E=∠C.
∵∠BFE=∠AFC,∴△BEF∽△ACF.
21.如图,已知△ABC中,∠ACB=90°,点D是边AB上一点,且△CDE∽△CAB.
(1)求证:△CAD∽△CBE;
(2)求证:EB⊥AB.
证明:(1)∵△CDE∽△CAB,
∴=,∠ACB=∠DCE,∴=,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE,
∴△CAD∽△CBE.
(2)∵△CAD∽△CBE,
∴∠CAD=∠CBE.
∵∠ACB=90°,
∴∠CAD+∠CBA=90°,
∴∠CBE+∠CBA=90°,
∴EB⊥AB.
22.在Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.如图①,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t s(0<t<2),连结PQ.
(1)若△BPQ与△ABC相似,求t的值;
解:由题意知,AB=10 cm,BP=5t cm,CQ=4t cm. BQ=(8-4t)cm.
当△PBQ∽△ABC时,有=,即=.解得t=1.
当△QBP∽△ABC时,有=,即=,解得t=.
∴当△BPQ与△ABC相似时,t=1或t=.
(2)如图②,连结AQ,CP,若AQ⊥CP,求t的值.
解:过点P作PM⊥BC于点M,则PM∥AC,设AQ,CP交于点N,如图所示.
易知△BMP∽△BCA,∴==,
∴==.∴PM=3t cm,BM=4t cm,
则CM=(8-4t)cm.
∵AQ⊥PC,∴∠ANC=90°,∴∠QAC+∠NCA=90°,
又∵∠PCM+∠NCA=90°,∴∠QAC=∠PCM.
又∵∠ACQ=∠PMC=90°,∴△ACQ∽△CMP,
∴=,∴=,解得t=.
23.如图,在等腰△ABC中,AB=AC,点M,N分别是BC,AC边上的点(M,N不与点B,C重合),且∠1=∠B.
(1)求证:∠BAM=∠CMN.
(2)若AB=5,BC=8,
①当BM=时,MN与AB是否平行 若平行,请证明;若不平行,请说明理由.
②当△AMN为等腰三角形时,求BM的长.
解:(1)∵∠1+∠CMN=∠B+∠BAM,∠1=∠B,
∴∠BAM=∠CMN.
(2)①MN∥AB.
理由:∵,∠B=∠B,
∴△ABM∽△CBA,∠BAM=∠C=∠1,∴MN∥AB.
②当AM=AN时,∠1=∠MNA,
∴点N与C重合,不合题意,应舍去;
当MA=MN时,△ABM≌△MCN,AB=MC=5,
∴BM=8-5=3;
当AN=MN时,∵△ABC∽△MCA,
∴,∴MC=,∴BM=.
综上所述,当△AMN是等腰三角形时,BM的长为3或.
24.如图1,在四边形ABCD中,E,F分别是AB,CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接GA,GB,GC,GD,EF,若∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD,BC所在直线互相垂直,求的值.
解:(1)∵GE是AB的垂直平分线,
∴GA=GB,同理GD=GC.
在△AGD和△BGC中,∵GA=GB,∠AGD=∠BGC,GD=GC,
∴△AGD≌△BGC,∴AD=BC.
(2)∵∠AGD=∠BGC,∴∠AGB=∠DGC.
在△AGB和△DGC中,,∠AGB=∠DGC,
∴△AGB∽△DGC.
∴,∠AGE=∠DGF,
∴∠AGD=∠EGF,∴△AGD∽△EGF.
(3).
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
