3.4.2.1 与相似三角形有关的高、角平分线和中线 同步练习题(含答案)
文档属性
| 名称 | 3.4.2.1 与相似三角形有关的高、角平分线和中线 同步练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览




文档简介
3.4 相似三角形的判定与性质
3.4.2 相似三角形的性质
第1课时 与相似三角形有关的高、角平分线和中线
一、选择题
1.【中考·重庆A卷】若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.【中考·重庆B卷】如图,△ABO∽△CDO,若AB=6,CD=2,则CD边上的高与AB边上的高之比是( )
A.1∶2 B.1∶3 C.2∶1 D.3∶1
第2题图 第6题图 第7题图 第8题图
3.已知△ABC∽△A′B′C′,BD和B′D′分别是两个三角形对应的角平分线,且AC∶A′C′=2∶3,若BD=4 cm,则B′D′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
4.【中考·兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
5.若两个相似三角形对应边上的高线之比为3:1,则对应角平分线之比为( )
A.9:1 B.6:1 C.3:1 D.:1
6.【2020·广西北部湾经济区】如图,在△ABC中,BC=120,高AD=60,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
7.【2020·淄博】如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列表达式中成立的是( )
A.a2+b2=5c2 B.a2+b2=4c2 C.a2+b2=3c2 D.a2+b2=2c2
8.【2020·海南】如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( )
A.1∶4 B.1∶3 C.2∶1 D.1∶2
10.已知D,E分别是△ABC中的AB,AC边上的点,DE∥BC,且AD∶BD=4∶5,那么△ADE与△ABC对应高的比是( )
A. B. C. D.
11.如图,在菱形ABCD中,E,F分别是边AB,AD的中点,连接CE,CF交对角线BD于点M,N,连接EF,则BM∶EF=( )
A.1∶1 B.1∶2 C.2∶3 D.3∶2
12.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的对应角平分线比为( )
A. B. C. D.
二、填空题
13.(1)相似三角形对应高的比等于________.
(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.
14.如图,已知在△ABC与△DEF中,∠A=∠D,∠B=∠E, CM,FN分别平分∠ACB,∠DFE.若=,AB=6,则DE的长为________.
第14题图 第16题图 第17题图 第18题图
15.如果两个相似三角形的两条对应边长分别是20 cm和25 cm,其中一个三角形最大内角的平分线长是12 cm,那么另一个三角形对应角的平分线长是____________cm.
16.【中考·柳州】如图,矩形EFGH内接于△ABC ,且边FG落在BC上,若BC=3,AD=2,EF=EH,则EH的长为___________.
17.如图,某校宣传栏后面2 m处种了一排树,每隔2 m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3 m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为 m.(不计宣传栏的厚度)
18.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何 ”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为 丈.(保留到整数,1丈=10尺)
三、解答题
19.已知△ABC∽△DEF,∠A=80°,∠E=70°,AB=5,DE=2.5,BC=8,DF=5.
(1)求∠B,∠C,∠D,∠F的度数;
(2)求AC,EF的长;
(3)求△ABC和△DEF的相似比;
(4)若AG,DH分别为△ABC和△DEF的高,求AG∶DH;
(5)若△ABC中∠C的平分线的长为a,求△DEF中∠F的平分线的长.
20.如图,在△ABC中,D,E分别是△ABC的边AB,AC上的点,DE∥BC,CF,EG分别是△ABC,△ADE的中线.已知AD∶DB=4∶3,EG=4,求CF的长.
21.如图,△ABC∽△A′B′C′,相似比为k,AD,A′D′分别是边BC,B′C′上的中线,求证:=k.
【建议读者进一步证明本课涉及的其它两条结论】
22.如图,已知在△ABC中, DE∥BC,AD=3,AB=5,DE与BC之间的距离GH为1.6,求BC边上的高AH.
23.三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图1的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积之和为S1;按图2的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的三角形面积之和为S2;继续操作下去……
(1)如图1,求和S1的值;
(2)第n次剪取后,求余下的所有三角形面积之和Sn.
24.已知△ABC的边BC长15 cm,高AH为10 cm,四边形DEFG内接于△ABC,点E,F在边BC上,点D,G分别在边AB,AC上,AH交DG于P.
(1)如图①,若四边形DEFG为正方形,求正方形的边长;
(2)如图②,若四边形DEFG为矩形,且DG∶DE=2∶1,求的值.
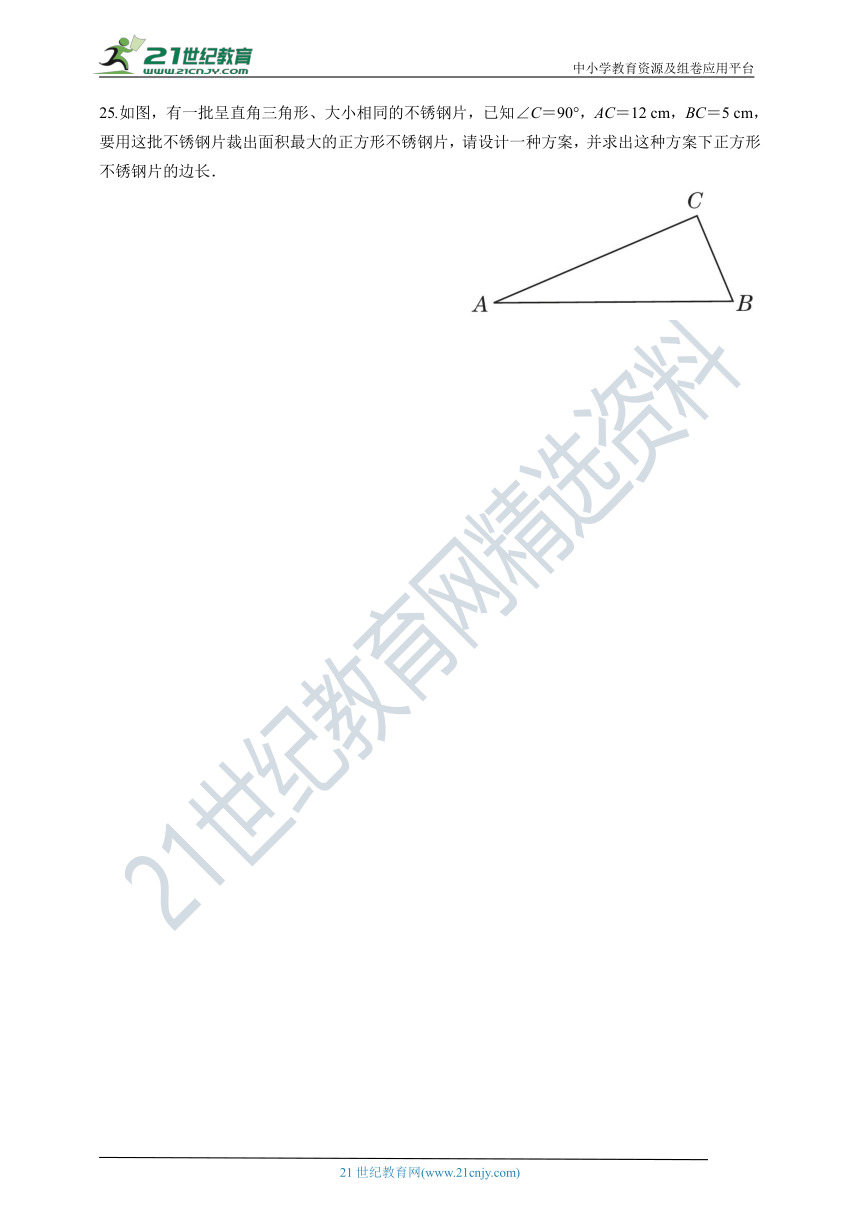
25.如图,有一批呈直角三角形、大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种方案下正方形不锈钢片的边长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·重庆A卷】若△ABC∽△DEF,相似比为3∶2,则对应高的比为( A )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.【中考·重庆B卷】如图,△ABO∽△CDO,若AB=6,CD=2,则CD边上的高与AB边上的高之比是( B )
A.1∶2 B.1∶3 C.2∶1 D.3∶1
第2题图 第6题图 第7题图 第8题图
3.已知△ABC∽△A′B′C′,BD和B′D′分别是两个三角形对应的角平分线,且AC∶A′C′=2∶3,若BD=4 cm,则B′D′的长是( C )
A.3 cm B.4 cm C.6 cm D.8 cm
4.【中考·兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( A )
A. B. C. D.
5.若两个相似三角形对应边上的高线之比为3:1,则对应角平分线之比为( C )
A.9:1 B.6:1 C.3:1 D.:1
【点拨】∵两个相似三角形对应高线之比为3:1,∴两个相似三角形的相似比为3:1,∴它们对应角平分线之比为3:1,故选C.
6.【2020·广西北部湾经济区】如图,在△ABC中,BC=120,高AD=60,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( B )
A.15 B.20 C.25 D.30
【点拨】设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC.
∴△AEF∽△ABC.
∵AD是△ABC的高,∴∠HDN=90°.
∴四边形EHDN是矩形.∴DN=EH=x,AN⊥EF.
∵△AEF∽△ABC,∴=(相似三角形对应边上的高的比等于相似比).∵AD=60,
∴AN=60-x.∴=,解得x=40.
∴AN=60-x=60-40=20.
7.【2020·淄博】如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列表达式中成立的是( A )
A.a2+b2=5c2 B.a2+b2=4c2 C.a2+b2=3c2 D.a2+b2=2c2
【点拨】设EF=x,DF=y,根据三角形重心的性质得AF=2DF=2y,BF=2EF=2x,利用勾股定理得到4x2+4y2=c2,4x2+y2=a2,x2+4y2=b2,然后利用加减消元法消去x,y得到a,b,c的关系.
8.【2020·海南】如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( C )
A.25 B.30 C.35 D.40
9.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( D )
A.1∶4 B.1∶3 C.2∶1 D.1∶2
10.已知D,E分别是△ABC中的AB,AC边上的点,DE∥BC,且AD∶BD=4∶5,那么△ADE与△ABC对应高的比是( D )
A. B. C. D.
11.如图,在菱形ABCD中,E,F分别是边AB,AD的中点,连接CE,CF交对角线BD于点M,N,连接EF,则BM∶EF=( C )
A.1∶1 B.1∶2 C.2∶3 D.3∶2
12.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的对应角平分线比为( B )
A. B. C. D.
二、填空题
13.(1)相似三角形对应高的比等于________.
(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.
【答案】相似比 相似比 相似比
14.如图,已知在△ABC与△DEF中,∠A=∠D,∠B=∠E, CM,FN分别平分∠ACB,∠DFE.若=,AB=6,则DE的长为________.
【答案】9
第14题图 第16题图 第17题图 第18题图
15.如果两个相似三角形的两条对应边长分别是20 cm和25 cm,其中一个三角形最大内角的平分线长是12 cm,那么另一个三角形对应角的平分线长是____________cm.
【点拨】设另一个三角形对应角的平分线长是x cm.
若已知角平分线的三角形是较小三角形,由题意得25∶20=x∶12,解得x=15;
若已知角平分线的三角形是较大三角形,由题意得20∶25=x∶12,解得x=9.6.
本题易错点是未进行分类讨论,直接把12 cm当作边长为20 cm的三角形的角平分线长.
【答案】15或9.6
16.【中考·柳州】如图,矩形EFGH内接于△ABC ,且边FG落在BC上,若BC=3,AD=2,EF=EH,则EH的长为___________.
【答案】
17.如图,某校宣传栏后面2 m处种了一排树,每隔2 m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3 m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为 m.(不计宣传栏的厚度)
【答案】6
18.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何 ”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为 丈.(保留到整数,1丈=10尺)
【答案】165
三、解答题
19.已知△ABC∽△DEF,∠A=80°,∠E=70°,AB=5,DE=2.5,BC=8,DF=5.
(1)求∠B,∠C,∠D,∠F的度数;
解:∵△ABC∽△DEF,∠A=80°,∠E=70°,
∴∠D=∠A=80°,∠B=∠E=70°,∠C=∠F=180°-80°-70°=30°.
(2)求AC,EF的长;
解:∵△ABC∽△DEF,AB=5,DE=2.5,
∴===.
又∵BC=8,DF=5,
∴AC=10,EF=4.
(3)求△ABC和△DEF的相似比;
解:由(2)得△ABC和△DEF的相似比是2∶1.
(4)若AG,DH分别为△ABC和△DEF的高,求AG∶DH;
若AG,DH分别为△ABC和△DEF的高,则AG∶DH=2∶1.
(5)若△ABC中∠C的平分线的长为a,求△DEF中∠F的平分线的长.
解:若△ABC中∠C的平分线的长为a,根据相似三角形对应的角平分线之比等于相似比,则△DEF中∠F的平分线的长为a.
20.如图,在△ABC中,D,E分别是△ABC的边AB,AC上的点,DE∥BC,CF,EG分别是△ABC,△ADE的中线.已知AD∶DB=4∶3,EG=4,求CF的长.
解:∵AD∶DB=4∶3,∴AD∶AB=4∶7.
又∵DE∥BC,∴△ABC∽△ADE.
∵CF,EG分别是△ABC与△ADE的中线,
∴=,∴=,
∴CF=7.
21.如图,△ABC∽△A′B′C′,相似比为k,AD,A′D′分别是边BC,B′C′上的中线,求证:=k.
证明:∵△ABC∽△A′B′C′,
∴===k,∠B=∠B′.
又∵AD,A′D′分别是边BC,B′C′上的中线,
∴==. ∴=.
又∵∠B=∠B′,∴△ABD∽△A′B′D′.
∴==k.
【建议读者进一步证明本课涉及的其它两条结论】
22.如图,已知在△ABC中, DE∥BC,AD=3,AB=5,DE与BC之间的距离GH为1.6,求BC边上的高AH.
解:∵DE∥BC,∴△ADE∽△ABC.
又∵AH为BC边上的高,∴AH⊥BC,AH⊥DE,
∴=.
设AG=x,则AH=x+1.6,
∴=,解得x=2.4.
经检验x=2.4是原方程的解,
∴AH=AG+GH=2.4+1.6=4.
23.三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图1的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积之和为S1;按图2的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的三角形面积之和为S2;继续操作下去……
(1)如图1,求和S1的值;
(2)第n次剪取后,求余下的所有三角形面积之和Sn.
解:(1)设CE的长为x,
由题意得AF=1-x,FD=x,
∵DF∥BC,∴△ADF∽△ABC,
∴,即,解得x=,
∴,
∴S1=×1×2-.
(2)同理可得S2=,S3=,
∴Sn=.
24.已知△ABC的边BC长15 cm,高AH为10 cm,四边形DEFG内接于△ABC,点E,F在边BC上,点D,G分别在边AB,AC上,AH交DG于P.
(1)如图①,若四边形DEFG为正方形,求正方形的边长;
解:设DG为x cm,
∵四边形DEFG是正方形,
∴DG∥BC,DG=DE=x cm,AP=(10-x)cm,
∴△ADG∽△ABC,
∴AP∶AH=DG∶BC,
即=,解得 x=6,
即正方形的边长为6 cm.
(2)如图②,若四边形DEFG为矩形,且DG∶DE=2∶1,求的值.
解:设DE=y cm,则DG=2y cm,
∵四边形DEFG是矩形,∴DG∥BC,AP=(10-y)cm,
∴△ADG∽△ABC,∴AP∶AH=DG∶BC,
即=,解得y=,∴2y=.
∵AD∶AB=DG∶BC=∶15=4∶7,∴=.
25.如图,有一批呈直角三角形、大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种方案下正方形不锈钢片的边长.
【点拨】要求面积最大的正方形,则正方形的顶点应落在△ABC的边上,而顶点落在边上时有如图①和图②两种情况,应分类讨论求解.
解:如图①,设正方形EFGH的边长为x cm,过点C作CD⊥AB于点D,交EH于点M.易知CM⊥EH.∵∠ACB=90°,AC=12 cm,BC=5 cm,
∴AB===13(cm).
∵AB·CD=AC·BC,∴CD===(cm).
又∵EH∥AB,∴△CEH∽△CAB.
∴=,即=,解得x=.
如图②,设正方形CEGH的边长为y cm.
∵GH∥AC,
∴△BHG∽△BCA.
∴=,
即=,解得y=.
∵<,∴应按图②裁剪,这时正方形不锈钢片的面积最大,它的边长为 cm.
3.4.2 相似三角形的性质
第1课时 与相似三角形有关的高、角平分线和中线
一、选择题
1.【中考·重庆A卷】若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.【中考·重庆B卷】如图,△ABO∽△CDO,若AB=6,CD=2,则CD边上的高与AB边上的高之比是( )
A.1∶2 B.1∶3 C.2∶1 D.3∶1
第2题图 第6题图 第7题图 第8题图
3.已知△ABC∽△A′B′C′,BD和B′D′分别是两个三角形对应的角平分线,且AC∶A′C′=2∶3,若BD=4 cm,则B′D′的长是( )
A.3 cm B.4 cm C.6 cm D.8 cm
4.【中考·兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( )
A. B. C. D.
5.若两个相似三角形对应边上的高线之比为3:1,则对应角平分线之比为( )
A.9:1 B.6:1 C.3:1 D.:1
6.【2020·广西北部湾经济区】如图,在△ABC中,BC=120,高AD=60,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
7.【2020·淄博】如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列表达式中成立的是( )
A.a2+b2=5c2 B.a2+b2=4c2 C.a2+b2=3c2 D.a2+b2=2c2
8.【2020·海南】如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( )
A.1∶4 B.1∶3 C.2∶1 D.1∶2
10.已知D,E分别是△ABC中的AB,AC边上的点,DE∥BC,且AD∶BD=4∶5,那么△ADE与△ABC对应高的比是( )
A. B. C. D.
11.如图,在菱形ABCD中,E,F分别是边AB,AD的中点,连接CE,CF交对角线BD于点M,N,连接EF,则BM∶EF=( )
A.1∶1 B.1∶2 C.2∶3 D.3∶2
12.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的对应角平分线比为( )
A. B. C. D.
二、填空题
13.(1)相似三角形对应高的比等于________.
(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.
14.如图,已知在△ABC与△DEF中,∠A=∠D,∠B=∠E, CM,FN分别平分∠ACB,∠DFE.若=,AB=6,则DE的长为________.
第14题图 第16题图 第17题图 第18题图
15.如果两个相似三角形的两条对应边长分别是20 cm和25 cm,其中一个三角形最大内角的平分线长是12 cm,那么另一个三角形对应角的平分线长是____________cm.
16.【中考·柳州】如图,矩形EFGH内接于△ABC ,且边FG落在BC上,若BC=3,AD=2,EF=EH,则EH的长为___________.
17.如图,某校宣传栏后面2 m处种了一排树,每隔2 m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3 m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为 m.(不计宣传栏的厚度)
18.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何 ”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为 丈.(保留到整数,1丈=10尺)
三、解答题
19.已知△ABC∽△DEF,∠A=80°,∠E=70°,AB=5,DE=2.5,BC=8,DF=5.
(1)求∠B,∠C,∠D,∠F的度数;
(2)求AC,EF的长;
(3)求△ABC和△DEF的相似比;
(4)若AG,DH分别为△ABC和△DEF的高,求AG∶DH;
(5)若△ABC中∠C的平分线的长为a,求△DEF中∠F的平分线的长.
20.如图,在△ABC中,D,E分别是△ABC的边AB,AC上的点,DE∥BC,CF,EG分别是△ABC,△ADE的中线.已知AD∶DB=4∶3,EG=4,求CF的长.
21.如图,△ABC∽△A′B′C′,相似比为k,AD,A′D′分别是边BC,B′C′上的中线,求证:=k.
【建议读者进一步证明本课涉及的其它两条结论】
22.如图,已知在△ABC中, DE∥BC,AD=3,AB=5,DE与BC之间的距离GH为1.6,求BC边上的高AH.
23.三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图1的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积之和为S1;按图2的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的三角形面积之和为S2;继续操作下去……
(1)如图1,求和S1的值;
(2)第n次剪取后,求余下的所有三角形面积之和Sn.
24.已知△ABC的边BC长15 cm,高AH为10 cm,四边形DEFG内接于△ABC,点E,F在边BC上,点D,G分别在边AB,AC上,AH交DG于P.
(1)如图①,若四边形DEFG为正方形,求正方形的边长;
(2)如图②,若四边形DEFG为矩形,且DG∶DE=2∶1,求的值.
25.如图,有一批呈直角三角形、大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种方案下正方形不锈钢片的边长.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【中考·重庆A卷】若△ABC∽△DEF,相似比为3∶2,则对应高的比为( A )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.【中考·重庆B卷】如图,△ABO∽△CDO,若AB=6,CD=2,则CD边上的高与AB边上的高之比是( B )
A.1∶2 B.1∶3 C.2∶1 D.3∶1
第2题图 第6题图 第7题图 第8题图
3.已知△ABC∽△A′B′C′,BD和B′D′分别是两个三角形对应的角平分线,且AC∶A′C′=2∶3,若BD=4 cm,则B′D′的长是( C )
A.3 cm B.4 cm C.6 cm D.8 cm
4.【中考·兰州】已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( A )
A. B. C. D.
5.若两个相似三角形对应边上的高线之比为3:1,则对应角平分线之比为( C )
A.9:1 B.6:1 C.3:1 D.:1
【点拨】∵两个相似三角形对应高线之比为3:1,∴两个相似三角形的相似比为3:1,∴它们对应角平分线之比为3:1,故选C.
6.【2020·广西北部湾经济区】如图,在△ABC中,BC=120,高AD=60,正方形EFGH的一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( B )
A.15 B.20 C.25 D.30
【点拨】设正方形EFGH的边长EF=EH=x,
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC.
∴△AEF∽△ABC.
∵AD是△ABC的高,∴∠HDN=90°.
∴四边形EHDN是矩形.∴DN=EH=x,AN⊥EF.
∵△AEF∽△ABC,∴=(相似三角形对应边上的高的比等于相似比).∵AD=60,
∴AN=60-x.∴=,解得x=40.
∴AN=60-x=60-40=20.
7.【2020·淄博】如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列表达式中成立的是( A )
A.a2+b2=5c2 B.a2+b2=4c2 C.a2+b2=3c2 D.a2+b2=2c2
【点拨】设EF=x,DF=y,根据三角形重心的性质得AF=2DF=2y,BF=2EF=2x,利用勾股定理得到4x2+4y2=c2,4x2+y2=a2,x2+4y2=b2,然后利用加减消元法消去x,y得到a,b,c的关系.
8.【2020·海南】如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( C )
A.25 B.30 C.35 D.40
9.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( D )
A.1∶4 B.1∶3 C.2∶1 D.1∶2
10.已知D,E分别是△ABC中的AB,AC边上的点,DE∥BC,且AD∶BD=4∶5,那么△ADE与△ABC对应高的比是( D )
A. B. C. D.
11.如图,在菱形ABCD中,E,F分别是边AB,AD的中点,连接CE,CF交对角线BD于点M,N,连接EF,则BM∶EF=( C )
A.1∶1 B.1∶2 C.2∶3 D.3∶2
12.已知△ABC∽△A'B'C'且相似比为,△A'B'C'∽△A″B″C″且相似比为,则△ABC与△A″B″C″的对应角平分线比为( B )
A. B. C. D.
二、填空题
13.(1)相似三角形对应高的比等于________.
(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.
【答案】相似比 相似比 相似比
14.如图,已知在△ABC与△DEF中,∠A=∠D,∠B=∠E, CM,FN分别平分∠ACB,∠DFE.若=,AB=6,则DE的长为________.
【答案】9
第14题图 第16题图 第17题图 第18题图
15.如果两个相似三角形的两条对应边长分别是20 cm和25 cm,其中一个三角形最大内角的平分线长是12 cm,那么另一个三角形对应角的平分线长是____________cm.
【点拨】设另一个三角形对应角的平分线长是x cm.
若已知角平分线的三角形是较小三角形,由题意得25∶20=x∶12,解得x=15;
若已知角平分线的三角形是较大三角形,由题意得20∶25=x∶12,解得x=9.6.
本题易错点是未进行分类讨论,直接把12 cm当作边长为20 cm的三角形的角平分线长.
【答案】15或9.6
16.【中考·柳州】如图,矩形EFGH内接于△ABC ,且边FG落在BC上,若BC=3,AD=2,EF=EH,则EH的长为___________.
【答案】
17.如图,某校宣传栏后面2 m处种了一排树,每隔2 m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3 m处,正好看到这排树两端的树干,其余的4棵均被挡住,那么宣传栏的长为 m.(不计宣传栏的厚度)
【答案】6
18.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何 ”译文如下:如图,今有山AB位于树的西面.山高AB为未知数,山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为 丈.(保留到整数,1丈=10尺)
【答案】165
三、解答题
19.已知△ABC∽△DEF,∠A=80°,∠E=70°,AB=5,DE=2.5,BC=8,DF=5.
(1)求∠B,∠C,∠D,∠F的度数;
解:∵△ABC∽△DEF,∠A=80°,∠E=70°,
∴∠D=∠A=80°,∠B=∠E=70°,∠C=∠F=180°-80°-70°=30°.
(2)求AC,EF的长;
解:∵△ABC∽△DEF,AB=5,DE=2.5,
∴===.
又∵BC=8,DF=5,
∴AC=10,EF=4.
(3)求△ABC和△DEF的相似比;
解:由(2)得△ABC和△DEF的相似比是2∶1.
(4)若AG,DH分别为△ABC和△DEF的高,求AG∶DH;
若AG,DH分别为△ABC和△DEF的高,则AG∶DH=2∶1.
(5)若△ABC中∠C的平分线的长为a,求△DEF中∠F的平分线的长.
解:若△ABC中∠C的平分线的长为a,根据相似三角形对应的角平分线之比等于相似比,则△DEF中∠F的平分线的长为a.
20.如图,在△ABC中,D,E分别是△ABC的边AB,AC上的点,DE∥BC,CF,EG分别是△ABC,△ADE的中线.已知AD∶DB=4∶3,EG=4,求CF的长.
解:∵AD∶DB=4∶3,∴AD∶AB=4∶7.
又∵DE∥BC,∴△ABC∽△ADE.
∵CF,EG分别是△ABC与△ADE的中线,
∴=,∴=,
∴CF=7.
21.如图,△ABC∽△A′B′C′,相似比为k,AD,A′D′分别是边BC,B′C′上的中线,求证:=k.
证明:∵△ABC∽△A′B′C′,
∴===k,∠B=∠B′.
又∵AD,A′D′分别是边BC,B′C′上的中线,
∴==. ∴=.
又∵∠B=∠B′,∴△ABD∽△A′B′D′.
∴==k.
【建议读者进一步证明本课涉及的其它两条结论】
22.如图,已知在△ABC中, DE∥BC,AD=3,AB=5,DE与BC之间的距离GH为1.6,求BC边上的高AH.
解:∵DE∥BC,∴△ADE∽△ABC.
又∵AH为BC边上的高,∴AH⊥BC,AH⊥DE,
∴=.
设AG=x,则AH=x+1.6,
∴=,解得x=2.4.
经检验x=2.4是原方程的解,
∴AH=AG+GH=2.4+1.6=4.
23.三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图1的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积之和为S1;按图2的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的三角形面积之和为S2;继续操作下去……
(1)如图1,求和S1的值;
(2)第n次剪取后,求余下的所有三角形面积之和Sn.
解:(1)设CE的长为x,
由题意得AF=1-x,FD=x,
∵DF∥BC,∴△ADF∽△ABC,
∴,即,解得x=,
∴,
∴S1=×1×2-.
(2)同理可得S2=,S3=,
∴Sn=.
24.已知△ABC的边BC长15 cm,高AH为10 cm,四边形DEFG内接于△ABC,点E,F在边BC上,点D,G分别在边AB,AC上,AH交DG于P.
(1)如图①,若四边形DEFG为正方形,求正方形的边长;
解:设DG为x cm,
∵四边形DEFG是正方形,
∴DG∥BC,DG=DE=x cm,AP=(10-x)cm,
∴△ADG∽△ABC,
∴AP∶AH=DG∶BC,
即=,解得 x=6,
即正方形的边长为6 cm.
(2)如图②,若四边形DEFG为矩形,且DG∶DE=2∶1,求的值.
解:设DE=y cm,则DG=2y cm,
∵四边形DEFG是矩形,∴DG∥BC,AP=(10-y)cm,
∴△ADG∽△ABC,∴AP∶AH=DG∶BC,
即=,解得y=,∴2y=.
∵AD∶AB=DG∶BC=∶15=4∶7,∴=.
25.如图,有一批呈直角三角形、大小相同的不锈钢片,已知∠C=90°,AC=12 cm,BC=5 cm,要用这批不锈钢片裁出面积最大的正方形不锈钢片,请设计一种方案,并求出这种方案下正方形不锈钢片的边长.
【点拨】要求面积最大的正方形,则正方形的顶点应落在△ABC的边上,而顶点落在边上时有如图①和图②两种情况,应分类讨论求解.
解:如图①,设正方形EFGH的边长为x cm,过点C作CD⊥AB于点D,交EH于点M.易知CM⊥EH.∵∠ACB=90°,AC=12 cm,BC=5 cm,
∴AB===13(cm).
∵AB·CD=AC·BC,∴CD===(cm).
又∵EH∥AB,∴△CEH∽△CAB.
∴=,即=,解得x=.
如图②,设正方形CEGH的边长为y cm.
∵GH∥AC,
∴△BHG∽△BCA.
∴=,
即=,解得y=.
∵<,∴应按图②裁剪,这时正方形不锈钢片的面积最大,它的边长为 cm.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
