4.2.2 由视图到立体图形-华师大版七年级数学上册教材配套教学课件(19张)
文档属性
| 名称 | 4.2.2 由视图到立体图形-华师大版七年级数学上册教材配套教学课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 14:23:22 | ||
图片预览


文档简介
(共19张PPT)
学习目标
能熟练地由三视图想象出物体形状,进一步提高空间想象能力.
由三视图想象出立体图形后能进行简单的面积或体积的计算.
根据三视图确定几何体
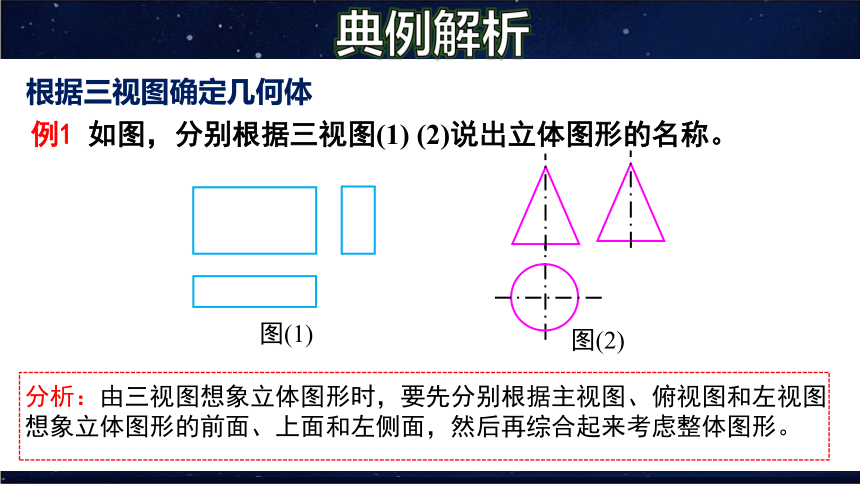
例1 如图,分别根据三视图(1) (2)说出立体图形的名称。
图(2)
图(1)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形。
典例解析
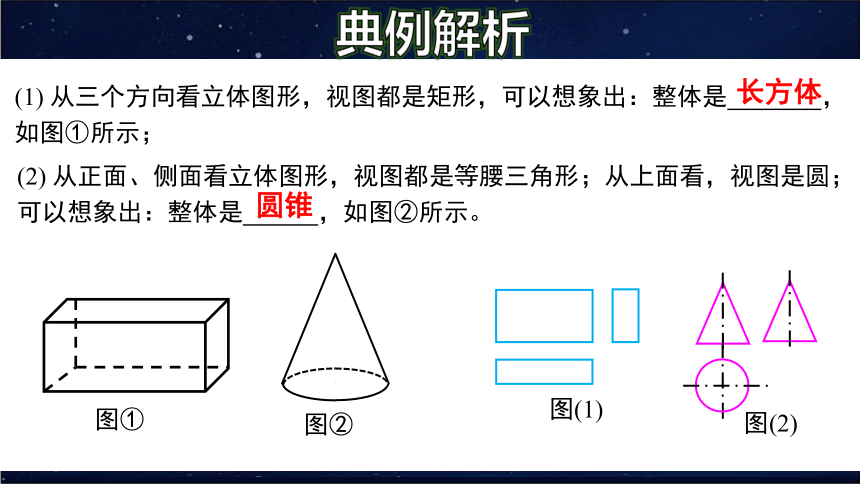
(1) 从三个方向看立体图形,视图都是矩形,可以想象出:整体是 ,如图①所示;
(2) 从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象出:整体是 ,如图②所示。
长方体
圆锥
图①
图②
图(2)
图(1)
典例解析
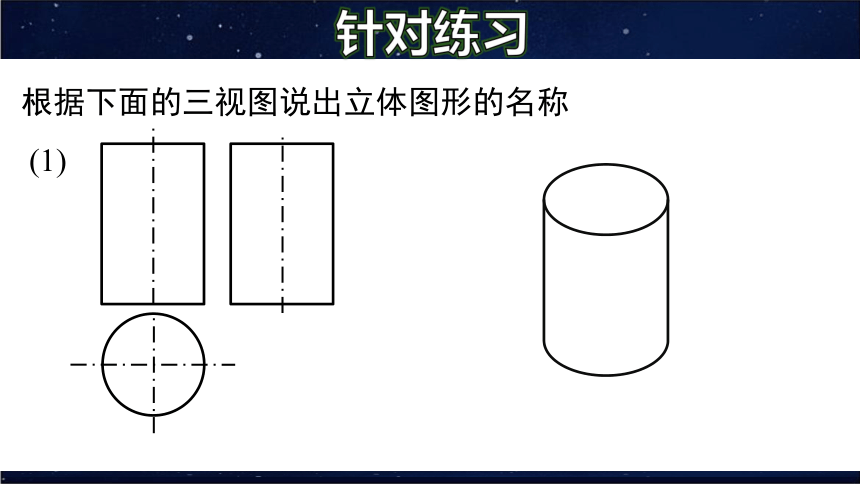
根据下面的三视图说出立体图形的名称
(1)
针对练习
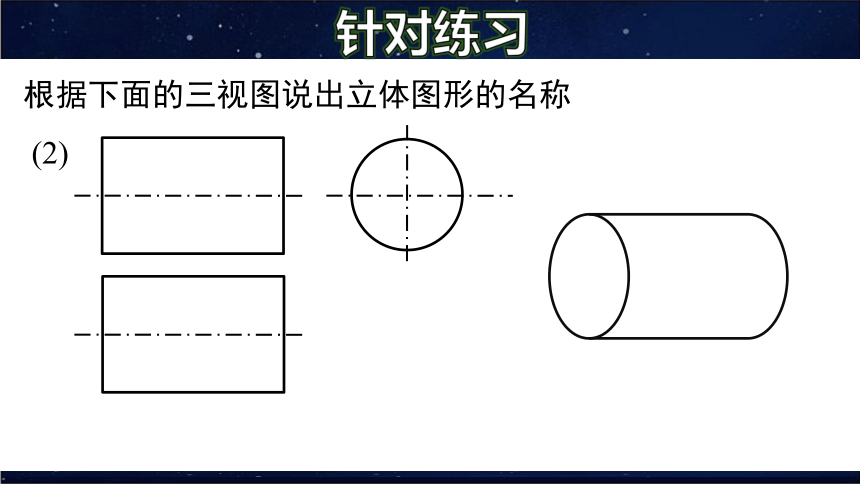
根据下面的三视图说出立体图形的名称
(2)
针对练习
方法总结:三视图除了与立体图形的形状有关外,还与立体图形的摆放位置有关,故由图想物,先根据三视图确定物体的形状,再确定物体的摆放位置。
根据下面的三视图说出立体图形的名称
(3)
针对练习
A
C
B
D
下面是哪个几何体的三视图?
主视图
左视图
俯视图
针对练习
例2 根据物体的三视图描述物体的形状
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面是矩形,它们的交线是一条棱 (中间的实线表示),可见到;综合各视图可知,物体的形状是正五棱柱。
典例解析
根据下列物体的三视图,填出几何体的名称:
(1) 如图①所示的几何体是__________;
(2) 如图②所示的几何体是_________。
图①
图②
正六棱柱
圆台
针对练习
根据三视图确定几何体的基本思路:
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形。
知识精讲
根据三视图确定几何体
三视图的有关计算
分析:
1. 应先由三视图想象出
;
2. 画出物体的 。
密封罐的立体形状
展开图
例3 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm)。
典例解析
解:由三视图可知,密封罐的形状是正六棱柱。
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm。
100mm
如图,是它的展开图。
由展开图可知,制作一个密封罐所需钢板的面积为:
典例解析
1. 三种图形的转化:
三视图
立体图
展开图
2. 由三视图求立体图形的面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高。
(2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分。
(3) 最后根据已知数据,求出展开图的面积。
三视图的有关计算
知识精讲
主
视
图
左
视
图
俯
视
图
8
8
13
1.如图是一个几何体的三视图。根据图示,可计算出该几何体的侧面积为 。
104π
针对练习
2. 如图是一个几何体的三视图,根据图中提供的数据 (单位:cm),可求得这个几何体的体积为 。
3 cm3
主视图 左视图 俯视图
3
1
1
针对练习
3. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为_______cm2。
2π
针对练习
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
由三视图求立体图形的体积 (或面积)
小结梳理
学习目标
能熟练地由三视图想象出物体形状,进一步提高空间想象能力.
由三视图想象出立体图形后能进行简单的面积或体积的计算.
根据三视图确定几何体
例1 如图,分别根据三视图(1) (2)说出立体图形的名称。
图(2)
图(1)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形。
典例解析
(1) 从三个方向看立体图形,视图都是矩形,可以想象出:整体是 ,如图①所示;
(2) 从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象出:整体是 ,如图②所示。
长方体
圆锥
图①
图②
图(2)
图(1)
典例解析
根据下面的三视图说出立体图形的名称
(1)
针对练习
根据下面的三视图说出立体图形的名称
(2)
针对练习
方法总结:三视图除了与立体图形的形状有关外,还与立体图形的摆放位置有关,故由图想物,先根据三视图确定物体的形状,再确定物体的摆放位置。
根据下面的三视图说出立体图形的名称
(3)
针对练习
A
C
B
D
下面是哪个几何体的三视图?
主视图
左视图
俯视图
针对练习
例2 根据物体的三视图描述物体的形状
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面是矩形,它们的交线是一条棱 (中间的实线表示),可见到;综合各视图可知,物体的形状是正五棱柱。
典例解析
根据下列物体的三视图,填出几何体的名称:
(1) 如图①所示的几何体是__________;
(2) 如图②所示的几何体是_________。
图①
图②
正六棱柱
圆台
针对练习
根据三视图确定几何体的基本思路:
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形。
知识精讲
根据三视图确定几何体
三视图的有关计算
分析:
1. 应先由三视图想象出
;
2. 画出物体的 。
密封罐的立体形状
展开图
例3 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm)。
典例解析
解:由三视图可知,密封罐的形状是正六棱柱。
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm。
100mm
如图,是它的展开图。
由展开图可知,制作一个密封罐所需钢板的面积为:
典例解析
1. 三种图形的转化:
三视图
立体图
展开图
2. 由三视图求立体图形的面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高。
(2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分。
(3) 最后根据已知数据,求出展开图的面积。
三视图的有关计算
知识精讲
主
视
图
左
视
图
俯
视
图
8
8
13
1.如图是一个几何体的三视图。根据图示,可计算出该几何体的侧面积为 。
104π
针对练习
2. 如图是一个几何体的三视图,根据图中提供的数据 (单位:cm),可求得这个几何体的体积为 。
3 cm3
主视图 左视图 俯视图
3
1
1
针对练习
3. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为_______cm2。
2π
针对练习
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
由三视图求立体图形的体积 (或面积)
小结梳理
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
