5.2.2 平行线的判定(三)-华师大版七年级数学上册教材配套教学课件(16张)
文档属性
| 名称 | 5.2.2 平行线的判定(三)-华师大版七年级数学上册教材配套教学课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 978.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 14:50:40 | ||
图片预览






文档简介
(共16张PPT)
理解并掌握平行线的判定方法三?
灵活运用平行线的判定方法解决问题?
学习目标
复习回顾
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
知识精讲
思考
如图,∠2和∠4为一组同旁内角,请猜想它们满足怎样的数量关系时a∥ b并说明理由.
温馨提示:能否借助已经学过的“ 平行线的判定方法”来说明下面的问题呢?
解: ∠2+∠4=180°。
理由:∵ ∠1+∠4=180° , ∠2+∠4=180° (已知)
∴∠1=∠2 (同角的补角相等)
∴ a∥ b (同位角相等,两直线平行)
知识精讲
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
∵∠2+∠4=180°(已知)
∴a∥ b(同旁内角互补,两直线平行)
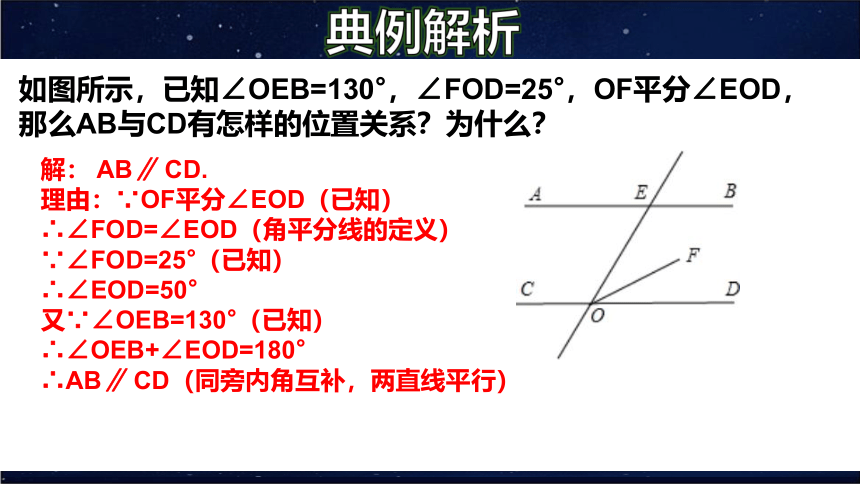
典例解析
如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,那么AB与CD有怎样的位置关系?为什么?
解: AB∥ CD.
理由:∵OF平分∠EOD(已知)
∴∠FOD=∠EOD(角平分线的定义)
∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠OEB=130°(已知)
∴∠OEB+∠EOD=180°
∴AB∥ CD(同旁内角互补,两直线平行)
典例解析
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:这两条直线平行.
∵b⊥a,c⊥a (已知)
∴∠1=∠2=90°(垂直的定义)
∴b∥ c(同位角相等,两直线平行)
理由:
a
b
c
达标检测
1.如图,下列说法正确的是( )
A.因为∠A+∠D=180°,所以AB∥ CD;
B.因为∠C+∠D=180°,所以AB∥ CD;
C.因为∠A+∠D=180°,所以AD∥ BC;
D.因为∠A+∠C=180°,所以AB∥ CD。
2.如图,已知直线AB,CD相交于点O,如果∠1=80°,那么当∠D是多少度时,DE∥AB?为什么?
解:∠D=100°.
∵∠1=80°(已知)
∴∠BOD=∠1=80°(对顶角相等)
∵∠D=100°(已知)
∴∠BOD+∠D=180°
∴DE∥AB (同旁内角互补,两直线平行)
A
达标检测
3.如图,直线EF分别交CD,AB于点M,N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是__________ .
A.∠A=∠C
B.∠E=∠F
C.AE∥FC
D.AB∥DC
D
达标检测
如图,能判定直线AB∥CD的条件是( ).
A.∠1=∠2
B.∠3=∠4
C.∠1+∠4=180°
D.∠3+∠4=90°
C
如图,已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证:AB∥CD.
解:∵∠B=142°,∠BFE=38°(已知)
∴∠B+∠BFE=180°
∴AB∥ EF(同旁内角互补,两直线平行)
又∵ ∠EFD=40°,∠D=140°(已知)
∴∠EFD+∠D=180°
∴EF∥ CD(同旁内角互补,两直线平行)
∴AB∥ CD(平面内平行于同一条直线的两条直线互相平行)
达标检测
达标检测
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,判断直线AB,CD是否平行,并说明理由.
达标检测
如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF,判断CM与DN是否平行,并说明理由.
CM与DN平行.
证明:∵∠1=70°,
∴∠BCF=180°-70°=110°,
∵CM平分∠DCF,
∴∠DCM=55°,
∵∠CDN=125°,
∴∠DCM+∠CDN=180°,
∴CM∥DN.
达标检测
如图,已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证:AB∥CD.
解:∵∠B=142°,∠BFE=38°,
∴∠B+∠BFE=180°,
∴AB∥EF,
又∵∠EFD+∠D=180°,
∴EF∥CD,
∴AB∥CD.
小结梳理
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
特殊方法
理解并掌握平行线的判定方法三?
灵活运用平行线的判定方法解决问题?
学习目标
复习回顾
判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
知识精讲
思考
如图,∠2和∠4为一组同旁内角,请猜想它们满足怎样的数量关系时a∥ b并说明理由.
温馨提示:能否借助已经学过的“ 平行线的判定方法”来说明下面的问题呢?
解: ∠2+∠4=180°。
理由:∵ ∠1+∠4=180° , ∠2+∠4=180° (已知)
∴∠1=∠2 (同角的补角相等)
∴ a∥ b (同位角相等,两直线平行)
知识精讲
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
∵∠2+∠4=180°(已知)
∴a∥ b(同旁内角互补,两直线平行)
典例解析
如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,那么AB与CD有怎样的位置关系?为什么?
解: AB∥ CD.
理由:∵OF平分∠EOD(已知)
∴∠FOD=∠EOD(角平分线的定义)
∵∠FOD=25°(已知)
∴∠EOD=50°
又∵∠OEB=130°(已知)
∴∠OEB+∠EOD=180°
∴AB∥ CD(同旁内角互补,两直线平行)
典例解析
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
答:这两条直线平行.
∵b⊥a,c⊥a (已知)
∴∠1=∠2=90°(垂直的定义)
∴b∥ c(同位角相等,两直线平行)
理由:
a
b
c
达标检测
1.如图,下列说法正确的是( )
A.因为∠A+∠D=180°,所以AB∥ CD;
B.因为∠C+∠D=180°,所以AB∥ CD;
C.因为∠A+∠D=180°,所以AD∥ BC;
D.因为∠A+∠C=180°,所以AB∥ CD。
2.如图,已知直线AB,CD相交于点O,如果∠1=80°,那么当∠D是多少度时,DE∥AB?为什么?
解:∠D=100°.
∵∠1=80°(已知)
∴∠BOD=∠1=80°(对顶角相等)
∵∠D=100°(已知)
∴∠BOD+∠D=180°
∴DE∥AB (同旁内角互补,两直线平行)
A
达标检测
3.如图,直线EF分别交CD,AB于点M,N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是__________ .
A.∠A=∠C
B.∠E=∠F
C.AE∥FC
D.AB∥DC
D
达标检测
如图,能判定直线AB∥CD的条件是( ).
A.∠1=∠2
B.∠3=∠4
C.∠1+∠4=180°
D.∠3+∠4=90°
C
如图,已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证:AB∥CD.
解:∵∠B=142°,∠BFE=38°(已知)
∴∠B+∠BFE=180°
∴AB∥ EF(同旁内角互补,两直线平行)
又∵ ∠EFD=40°,∠D=140°(已知)
∴∠EFD+∠D=180°
∴EF∥ CD(同旁内角互补,两直线平行)
∴AB∥ CD(平面内平行于同一条直线的两条直线互相平行)
达标检测
达标检测
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,判断直线AB,CD是否平行,并说明理由.
达标检测
如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF,判断CM与DN是否平行,并说明理由.
CM与DN平行.
证明:∵∠1=70°,
∴∠BCF=180°-70°=110°,
∵CM平分∠DCF,
∴∠DCM=55°,
∵∠CDN=125°,
∴∠DCM+∠CDN=180°,
∴CM∥DN.
达标检测
如图,已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证:AB∥CD.
解:∵∠B=142°,∠BFE=38°,
∴∠B+∠BFE=180°,
∴AB∥EF,
又∵∠EFD+∠D=180°,
∴EF∥CD,
∴AB∥CD.
小结梳理
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
特殊方法
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
