26.2.3 求二次函数的表达式课件 华师大版九年级数学下册(18张)
文档属性
| 名称 | 26.2.3 求二次函数的表达式课件 华师大版九年级数学下册(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
九年级(下)
新华东师大版第26章 二次函数
第9课时 求二次函数的表达式
(Ⅰ)一般式:
(Ⅱ)顶点式:
(Ⅲ)交点式:
情境激疑
想一想:以前我们是如何求一次函数或反比例函数的表达式呢?
待定系数法
如何求二次函数 的表达式呢?
探究发现
问题1:一个二次函数的图象经过(0,1)、(2,4)、(3,10)
三点,求这个二次函数的解析式。
(1)设二次函数的解析式为: ,如何求出a,b,c
(2)解这个方程组得:
(3)你能写出这个二次函数的解析式吗?
学以致用
例 1
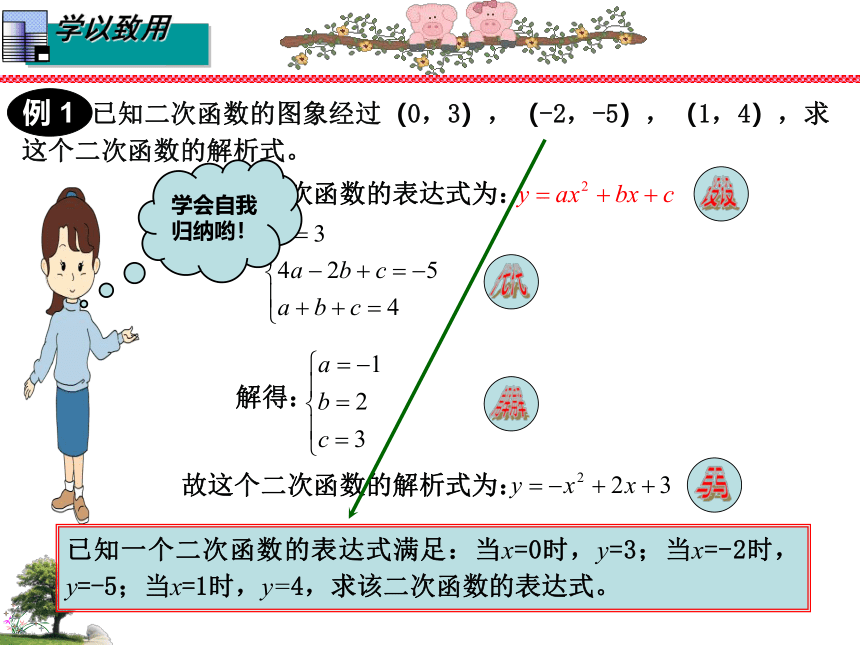
已知二次函数的图象经过(0,3),(-2,-5),(1,4),求
这个二次函数的解析式。
解:设二次函数的表达式为:
解得:
故这个二次函数的解析式为:
学会自我归纳哟!
已知一个二次函数的表达式满足:当x=0时,y=3;当x=-2时,y=-5;当x=1时,y=4,求该二次函数的表达式。
探究发现
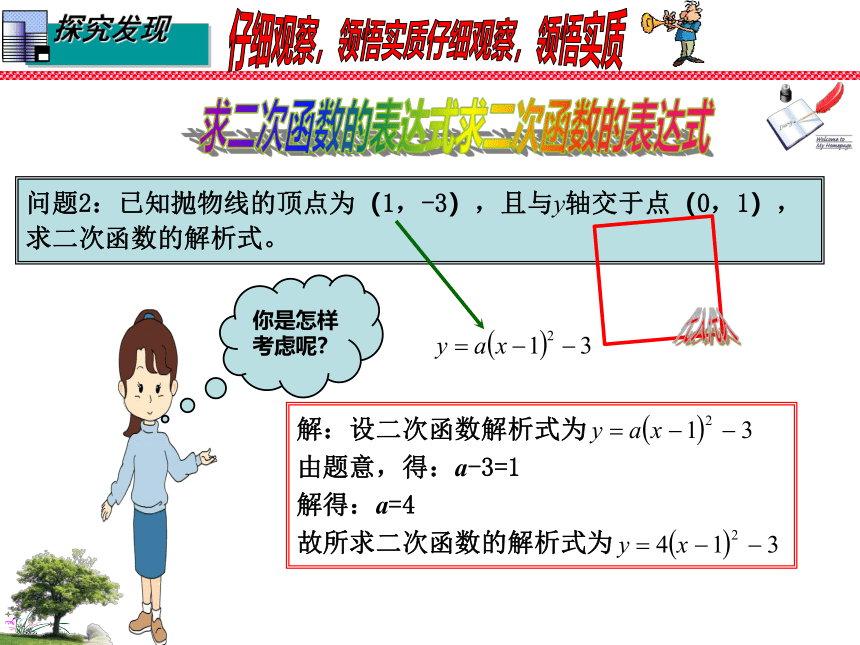
问题2:已知抛物线的顶点为(1,-3),且与y轴交于点(0,1),求二次函数的解析式。
你是怎样考虑呢?
解:设二次函数解析式为
由题意,得:a-3=1
解得:a=4
故所求二次函数的解析式为
探究发现
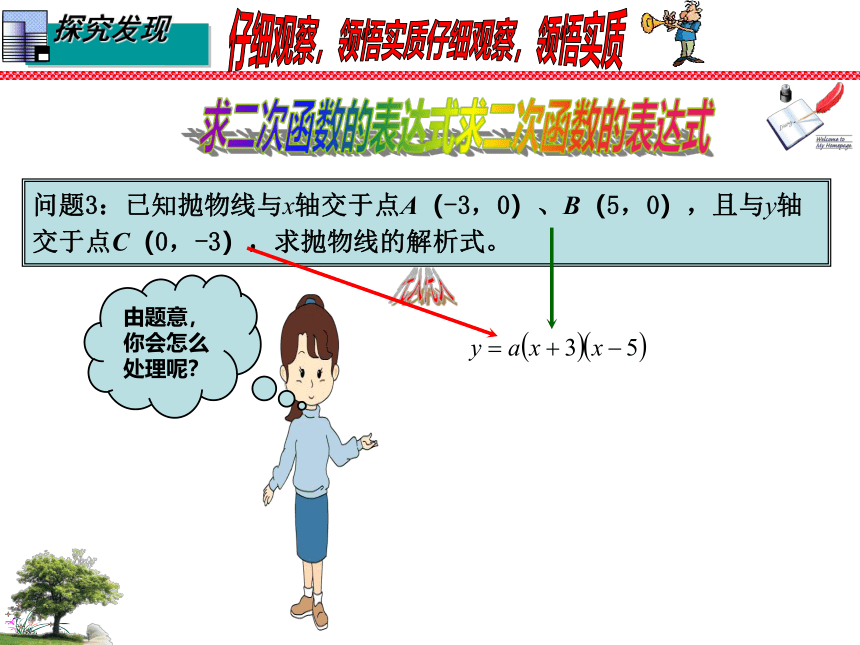
问题3:已知抛物线与x轴交于点A(-3,0)、B(5,0),且与y轴交于点C(0,-3),求抛物线的解析式。
由题意,你会怎么处理呢?
探究发现
类型 基本形式 适用情况
一般式
顶点式
交点式
已知图象上任意三点。
已知抛物线顶点坐标和另一个点的坐标。
已知抛物线与x轴的两个交点坐标及另一个点的坐标。
探究发现
(Ⅰ)设出适当的二次函数解析式形式;
(Ⅱ)代入点的坐标构成方程(组);
(Ⅲ)解方程(组)求出待定系数的值;
(Ⅳ)写出二次函数的解析式并化为一般形式。
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
A
O
C
B
x
y
D
解:配方得:
∵A、B两点关于x=-1对称
∴连结BC,交直线x=-1于点D
设线段BC的解析式为:
∴ 解得:
故线段BC的解析式为:
当x=-1时,y=2
故对称轴上存在点D(-1,2),使得AD+CD的值最小。
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(3)在(1)中的抛物线上是否存在一点E,使△ABE的面积为10,若存
在,求出点E的坐标。
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
A
O
C
B
x
y
E
?
F
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(3)在(1)中的抛物线上是否存在一点E,使△ABE的面积为10,若存
在,求出点E的坐标。
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
?
(4)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面
积最大?若存在,求出点P的坐标及△PBC的面积最大值。若不存在,
请说明理由。
A
O
C
B
x
y
P
数 学 活 动 室
学 以 致 用
根据下列条件,求二次函数的表达式:
(2)二次函数的图象过A、B、C三点,点A的坐标为(-1,0),
点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)已知二次函数 ,当x=0时,y=1;当x=-1时, y=6;
当x=1时,y=0.
(3)当x=-1时,抛物线的最高点的纵坐标为4,且与x轴两交点之
间的距离为6.
A
O
C
B
x
y
(2)
O
x
y
(3)
数 学 活 动 室
学 以 致 用
2.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),以x轴交于C、D两点,点P是x轴上的一个动点。
(1)求此抛物线对应的函数表达式;
(2)当PA+PB的值最小时,求点P的坐标。
A
O
B
D
x
y
3
C
4
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.2
P 23
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第26章 二次函数
第9课时 求二次函数的表达式
(Ⅰ)一般式:
(Ⅱ)顶点式:
(Ⅲ)交点式:
情境激疑
想一想:以前我们是如何求一次函数或反比例函数的表达式呢?
待定系数法
如何求二次函数 的表达式呢?
探究发现
问题1:一个二次函数的图象经过(0,1)、(2,4)、(3,10)
三点,求这个二次函数的解析式。
(1)设二次函数的解析式为: ,如何求出a,b,c
(2)解这个方程组得:
(3)你能写出这个二次函数的解析式吗?
学以致用
例 1
已知二次函数的图象经过(0,3),(-2,-5),(1,4),求
这个二次函数的解析式。
解:设二次函数的表达式为:
解得:
故这个二次函数的解析式为:
学会自我归纳哟!
已知一个二次函数的表达式满足:当x=0时,y=3;当x=-2时,y=-5;当x=1时,y=4,求该二次函数的表达式。
探究发现
问题2:已知抛物线的顶点为(1,-3),且与y轴交于点(0,1),求二次函数的解析式。
你是怎样考虑呢?
解:设二次函数解析式为
由题意,得:a-3=1
解得:a=4
故所求二次函数的解析式为
探究发现
问题3:已知抛物线与x轴交于点A(-3,0)、B(5,0),且与y轴交于点C(0,-3),求抛物线的解析式。
由题意,你会怎么处理呢?
探究发现
类型 基本形式 适用情况
一般式
顶点式
交点式
已知图象上任意三点。
已知抛物线顶点坐标和另一个点的坐标。
已知抛物线与x轴的两个交点坐标及另一个点的坐标。
探究发现
(Ⅰ)设出适当的二次函数解析式形式;
(Ⅱ)代入点的坐标构成方程(组);
(Ⅲ)解方程(组)求出待定系数的值;
(Ⅳ)写出二次函数的解析式并化为一般形式。
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
A
O
C
B
x
y
D
解:配方得:
∵A、B两点关于x=-1对称
∴连结BC,交直线x=-1于点D
设线段BC的解析式为:
∴ 解得:
故线段BC的解析式为:
当x=-1时,y=2
故对称轴上存在点D(-1,2),使得AD+CD的值最小。
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(3)在(1)中的抛物线上是否存在一点E,使△ABE的面积为10,若存
在,求出点E的坐标。
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
A
O
C
B
x
y
E
?
F
学以致用
例 2
如图,抛物线 与x轴交于点A(1,0)和点B,且过
点C(0,3).
(1)求该抛物线的表达式;
(3)在(1)中的抛物线上是否存在一点E,使△ABE的面积为10,若存
在,求出点E的坐标。
(2)在(1)中的抛物线上对称轴上是否存在点D,使AD+CD的值最小,
若存在,求出点D的坐标,若不存在,请说明理由。
?
(4)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面
积最大?若存在,求出点P的坐标及△PBC的面积最大值。若不存在,
请说明理由。
A
O
C
B
x
y
P
数 学 活 动 室
学 以 致 用
根据下列条件,求二次函数的表达式:
(2)二次函数的图象过A、B、C三点,点A的坐标为(-1,0),
点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)已知二次函数 ,当x=0时,y=1;当x=-1时, y=6;
当x=1时,y=0.
(3)当x=-1时,抛物线的最高点的纵坐标为4,且与x轴两交点之
间的距离为6.
A
O
C
B
x
y
(2)
O
x
y
(3)
数 学 活 动 室
学 以 致 用
2.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),以x轴交于C、D两点,点P是x轴上的一个动点。
(1)求此抛物线对应的函数表达式;
(2)当PA+PB的值最小时,求点P的坐标。
A
O
B
D
x
y
3
C
4
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.2
P 23
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
