华师大版九年级下册数学26.3 实践与探索 --- 商品经济利润最大问题课件(14张PPT)
文档属性
| 名称 | 华师大版九年级下册数学26.3 实践与探索 --- 商品经济利润最大问题课件(14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:22:15 | ||
图片预览






文档简介
(共14张PPT)
第3课时 商品经济利润最大问题
情境激疑
问题:草莓是云南多地盛产的水果。今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元。经试销发现,销售量y(千克)与销售价x(元/千克)符合一次函数关系式,如图是y与x的函数关系图象。
(1)求y与x的函数表达式,请直接写出x的取值范围;
(2)设该水果销售店试销草莓得到的利润为W(元),求W的最大值。
40
30
20
10
x(元/千克)
260
280
300
y(千克)
O
九年级(下)
新华东师大版第26章 二次函数
探究发现
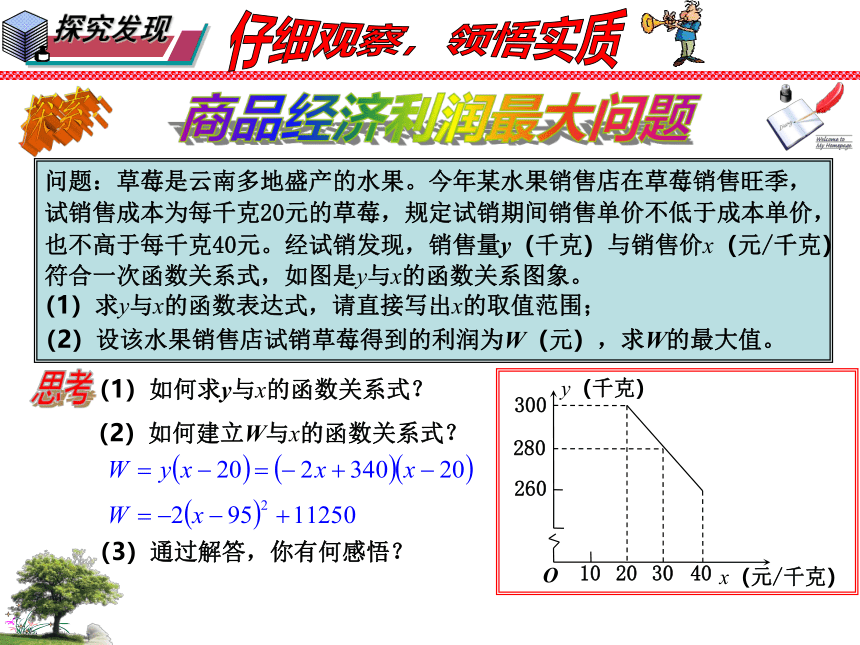
(2)如何建立W与x的函数关系式?
(1)如何求y与x的函数关系式?
问题:草莓是云南多地盛产的水果。今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元。经试销发现,销售量y(千克)与销售价x(元/千克)符合一次函数关系式,如图是y与x的函数关系图象。
(1)求y与x的函数表达式,请直接写出x的取值范围;
(2)设该水果销售店试销草莓得到的利润为W(元),求W的最大值。
40
30
20
10
x(元/千克)
260
280
300
y(千克)
O
(3)通过解答,你有何感悟?
探究发现
(Ⅰ)解答这类题的关键是将实际问题转化求函数最值问题,解这类题,
既要看到销售价格对销售量的影响,也要看到销售价格对单件商品
利润产生的影响,两者结合起来,销售价格就会对销售总利润产生
影响。
(Ⅱ)利润公式:总利润=单个利润×销售量=总销售额-总成本;
利润=售价-进价;
(Ⅲ)利用二次函数的性质解决生活中的最大值或最小值问题,一般方法是:
①列出二次函数的表达式,列表达式时,要根据自变量的实际意义,确定自变量的取值范围;
②在自变量取值范围内,运用公式法或配方法求出二次函数的最大值或最小值。
学以致用
例 1
某商场销售一种商品,进价为每个20元,规定每个商品售价不低于
进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) …… 30 40 50 ……
每天的销售量y(个) …… 100 80 60 ……
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为W(元),求W与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利
润最大?最大利润是多少元?
数 学 活 动 室
学 以 致 用
1.某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件。经过市场调查,发现这种商品的销售单价每降低1元,其日销售量可增加8件。设该商品每件降价x元,商场一天可通过A商品获得利润y元。
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场通过A商品所获利润最大?
数 学 活 动 室
学 以 致 用
2.某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20千克。
(1)设每千克水果降价x元,平均每天盈利y元,试写出y与x之间
的函数关系式;
(2)若要平均每天盈利960元,则每千克应降价多少元?
(3)要使销售这种水果每天获利最大,每千克应降价多少元?最
大利润是多少元?
学以致用
例 2
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时
房间会全部住满。当每个房间每天的房价每增加10元时,就会有一个房间空闲。设每个房间的房价每天增加x元(x为10 的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
变式1:若“宾馆需对游客居住的每个房间每天支出20元的各种费用”,其余条件不变,又该如何解答?
变式2:若“宾馆需对游客居住的每个房间每天支出20元的各种费用,根据规定,每个房间每天的房价不得高于340元。”,其余条件不变,又该如何解答?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
学有所成
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
习题 26.3
P 28
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
第3课时 商品经济利润最大问题
情境激疑
问题:草莓是云南多地盛产的水果。今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元。经试销发现,销售量y(千克)与销售价x(元/千克)符合一次函数关系式,如图是y与x的函数关系图象。
(1)求y与x的函数表达式,请直接写出x的取值范围;
(2)设该水果销售店试销草莓得到的利润为W(元),求W的最大值。
40
30
20
10
x(元/千克)
260
280
300
y(千克)
O
九年级(下)
新华东师大版第26章 二次函数
探究发现
(2)如何建立W与x的函数关系式?
(1)如何求y与x的函数关系式?
问题:草莓是云南多地盛产的水果。今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元。经试销发现,销售量y(千克)与销售价x(元/千克)符合一次函数关系式,如图是y与x的函数关系图象。
(1)求y与x的函数表达式,请直接写出x的取值范围;
(2)设该水果销售店试销草莓得到的利润为W(元),求W的最大值。
40
30
20
10
x(元/千克)
260
280
300
y(千克)
O
(3)通过解答,你有何感悟?
探究发现
(Ⅰ)解答这类题的关键是将实际问题转化求函数最值问题,解这类题,
既要看到销售价格对销售量的影响,也要看到销售价格对单件商品
利润产生的影响,两者结合起来,销售价格就会对销售总利润产生
影响。
(Ⅱ)利润公式:总利润=单个利润×销售量=总销售额-总成本;
利润=售价-进价;
(Ⅲ)利用二次函数的性质解决生活中的最大值或最小值问题,一般方法是:
①列出二次函数的表达式,列表达式时,要根据自变量的实际意义,确定自变量的取值范围;
②在自变量取值范围内,运用公式法或配方法求出二次函数的最大值或最小值。
学以致用
例 1
某商场销售一种商品,进价为每个20元,规定每个商品售价不低于
进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) …… 30 40 50 ……
每天的销售量y(个) …… 100 80 60 ……
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为W(元),求W与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利
润最大?最大利润是多少元?
数 学 活 动 室
学 以 致 用
1.某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件。经过市场调查,发现这种商品的销售单价每降低1元,其日销售量可增加8件。设该商品每件降价x元,商场一天可通过A商品获得利润y元。
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场通过A商品所获利润最大?
数 学 活 动 室
学 以 致 用
2.某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可多售出20千克。
(1)设每千克水果降价x元,平均每天盈利y元,试写出y与x之间
的函数关系式;
(2)若要平均每天盈利960元,则每千克应降价多少元?
(3)要使销售这种水果每天获利最大,每千克应降价多少元?最
大利润是多少元?
学以致用
例 2
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时
房间会全部住满。当每个房间每天的房价每增加10元时,就会有一个房间空闲。设每个房间的房价每天增加x元(x为10 的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
变式1:若“宾馆需对游客居住的每个房间每天支出20元的各种费用”,其余条件不变,又该如何解答?
变式2:若“宾馆需对游客居住的每个房间每天支出20元的各种费用,根据规定,每个房间每天的房价不得高于340元。”,其余条件不变,又该如何解答?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
学有所成
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
习题 26.3
P 28
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
