九年级下册数学华师大版26.3 实践与探索---几何图形面积最值问题课件(15张PPT)
文档属性
| 名称 | 九年级下册数学华师大版26.3 实践与探索---几何图形面积最值问题课件(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:23:46 | ||
图片预览




文档简介
(共15张PPT)
第2课时 几何图形面积最值问题
(Ⅰ)利用二次函数解决运动路线的最高(远)问题:
(Ⅱ)利用二次函数解决实物模型的高(宽)度问题:
物体运动的路线是抛物线形时,求最高就是求抛物线顶点的纵坐标,求最远就是求抛物线与x轴的交点的横坐标。
在此基础上,今天我们将利用二次函数的相关知识解决几何图形面积最大(小)问题。
九年级(下)
新华东师大版第26章 二次函数
情境激疑
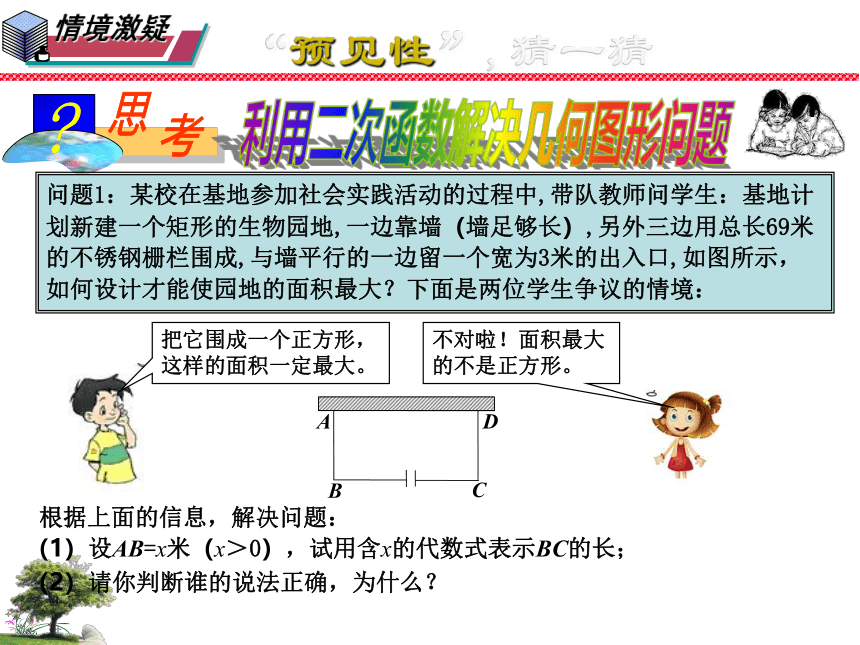
问题1:某校在基地参加社会实践活动的过程中,带队教师问学生:基地计划新建一个矩形的生物园地,一边靠墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境:
A
B
C
D
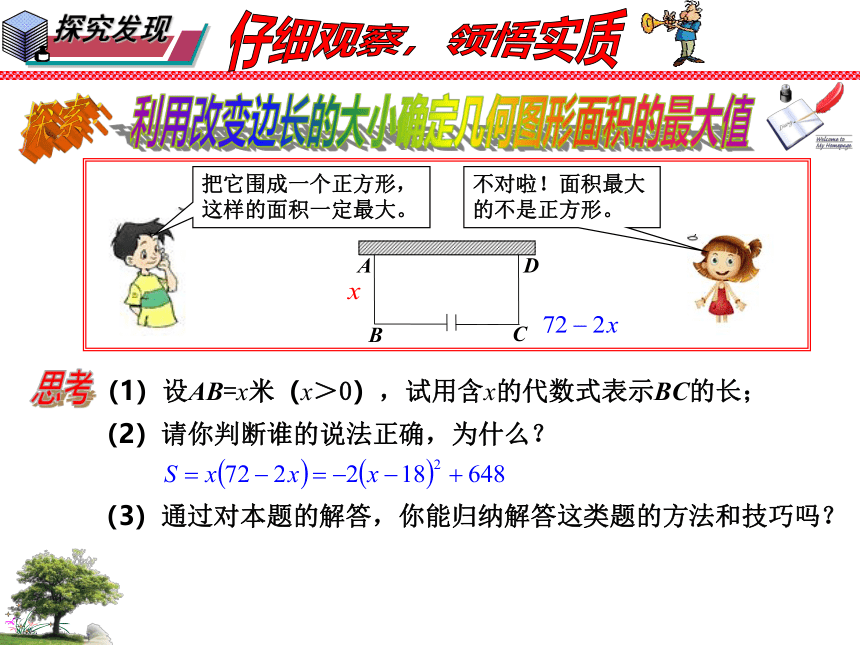
把它围成一个正方形,这样的面积一定最大。
不对啦!面积最大的不是正方形。
根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
探究发现
(2)请你判断谁的说法正确,为什么?
(3)通过对本题的解答,你能归纳解答这类题的方法和技巧吗?
A
B
C
D
把它围成一个正方形,这样的面积一定最大。
不对啦!面积最大的不是正方形。
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
探究发现
(Ⅰ)仔细审题,把实际问题转化为二次函数问题,用函数表达式
表示出面积S与所设未知数x之间的关系。
(Ⅱ)利用二次函数图象的顶点坐标求出S取最值时x的值。
说说你的感悟吧!
学以致用
例 1
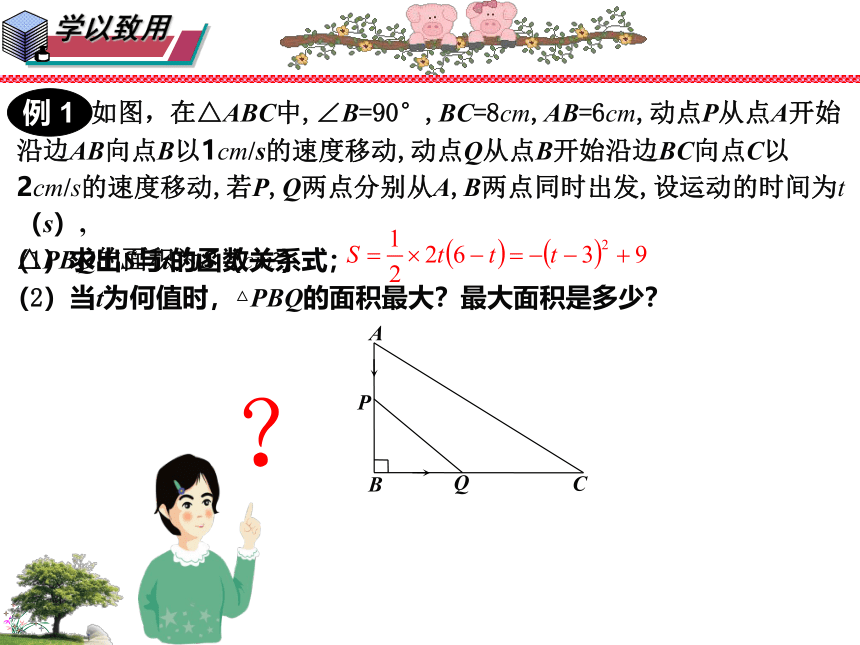
如图,在△ABC中,∠B=90°,BC=8cm,AB=6cm,动点P从点A开始
沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动,若P,Q两点分别从A,B两点同时出发,设运动的时间为t(s),
△PBQ的面积为S(cm2).
?
(1)求出S与t的函数关系式;
(2)当t为何值时,△PBQ的面积最大?最大面积是多少?
A
B
C
Q
P
探究发现
问题2:如图,已知抛物线 经过A(3,0),B(0,3),两点.取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这个橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A、B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标,如果不存在,请简要说明理由。
B
A
O
P
x
y
?
探究发现
(3,0)
(3)通过对本题的解答,你能归纳解答这类题的方法和技巧吗?
B
A
O
P
x
y
D
N
(0,3)
(1)你能否求出二次函数 的解析式,如何求?
(2)设点P的坐标为 ,如何表示△PAB的面积?
探究发现
(Ⅰ)利用割补法把一个三角形分成两个三角形,巧妙地假设点P的
横坐标为x,利用铅垂高表示出三角形面积的函数表达式,然
后利用二次函数的性质求出面积的最大值是解决这类问题的
常用方法。
(Ⅱ)利用铅垂高来求三角形的面积不失为一种好的方法。
学以致用
例 2
如图,二次函数 的图象经过点A(2,4)和点B(6,0).
(1)求a,b的值;
(2)若点C是该二次函数图象上A、B两点之间的一个动点,横坐标为x
(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达
式,并求出S的最大值。
D
?
A
B
C
O
x
y
F
E
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.3
P 28
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
第2课时 几何图形面积最值问题
(Ⅰ)利用二次函数解决运动路线的最高(远)问题:
(Ⅱ)利用二次函数解决实物模型的高(宽)度问题:
物体运动的路线是抛物线形时,求最高就是求抛物线顶点的纵坐标,求最远就是求抛物线与x轴的交点的横坐标。
在此基础上,今天我们将利用二次函数的相关知识解决几何图形面积最大(小)问题。
九年级(下)
新华东师大版第26章 二次函数
情境激疑
问题1:某校在基地参加社会实践活动的过程中,带队教师问学生:基地计划新建一个矩形的生物园地,一边靠墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境:
A
B
C
D
把它围成一个正方形,这样的面积一定最大。
不对啦!面积最大的不是正方形。
根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
探究发现
(2)请你判断谁的说法正确,为什么?
(3)通过对本题的解答,你能归纳解答这类题的方法和技巧吗?
A
B
C
D
把它围成一个正方形,这样的面积一定最大。
不对啦!面积最大的不是正方形。
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
探究发现
(Ⅰ)仔细审题,把实际问题转化为二次函数问题,用函数表达式
表示出面积S与所设未知数x之间的关系。
(Ⅱ)利用二次函数图象的顶点坐标求出S取最值时x的值。
说说你的感悟吧!
学以致用
例 1
如图,在△ABC中,∠B=90°,BC=8cm,AB=6cm,动点P从点A开始
沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动,若P,Q两点分别从A,B两点同时出发,设运动的时间为t(s),
△PBQ的面积为S(cm2).
?
(1)求出S与t的函数关系式;
(2)当t为何值时,△PBQ的面积最大?最大面积是多少?
A
B
C
Q
P
探究发现
问题2:如图,已知抛物线 经过A(3,0),B(0,3),两点.取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这个橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A、B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标,如果不存在,请简要说明理由。
B
A
O
P
x
y
?
探究发现
(3,0)
(3)通过对本题的解答,你能归纳解答这类题的方法和技巧吗?
B
A
O
P
x
y
D
N
(0,3)
(1)你能否求出二次函数 的解析式,如何求?
(2)设点P的坐标为 ,如何表示△PAB的面积?
探究发现
(Ⅰ)利用割补法把一个三角形分成两个三角形,巧妙地假设点P的
横坐标为x,利用铅垂高表示出三角形面积的函数表达式,然
后利用二次函数的性质求出面积的最大值是解决这类问题的
常用方法。
(Ⅱ)利用铅垂高来求三角形的面积不失为一种好的方法。
学以致用
例 2
如图,二次函数 的图象经过点A(2,4)和点B(6,0).
(1)求a,b的值;
(2)若点C是该二次函数图象上A、B两点之间的一个动点,横坐标为x
(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达
式,并求出S的最大值。
D
?
A
B
C
O
x
y
F
E
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
练习题 26.3
P 28
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
