华师大版九年级下册数学27.1.2 圆的对称性--圆心角定理课件(15张ppt)
文档属性
| 名称 | 华师大版九年级下册数学27.1.2 圆的对称性--圆心角定理课件(15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:25:46 | ||
图片预览





文档简介
(共15张PPT)
九年级(下)
新华东师大版第27章 圆
情境激疑
问题1:请同学们思考并解答下列问题:
圆既是轴对称图形,又是中心对称图形,也是旋转对称图形。对称轴是过圆心的任意一条直线,对称中心和旋转中心都是圆心,旋转角度可以是任意角度。
(1)圆是对称图形吗?它有哪些对称性?
(2)能否用手中的圆演示出它的各种对称性呢?
(3)圆的对称轴是什么?对称中心和旋转中心是什么?
探究发现
O
A
B
C
C'
A'
B'
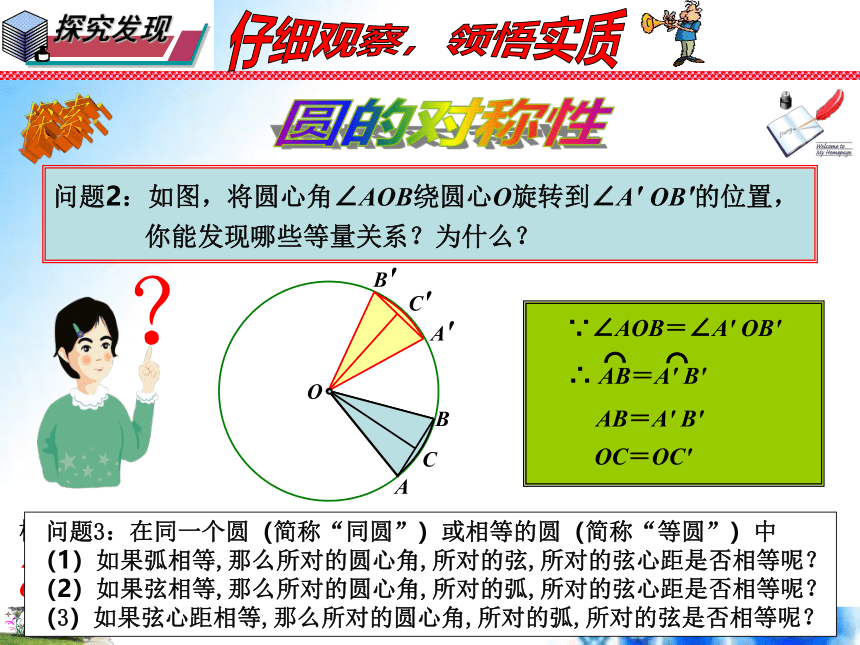
问题2:如图,将圆心角∠AOB绕圆心O旋转到∠A' OB'的位置,
你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A' OB'的位置时,显然∠AOB=∠A' OB' ,射线OA与OA'重合,OB与OB'重合。而同圆的半径相等,OA=OA' ,OB=OB' ,从而点A与A'重合,B与B'重合.
∵∠AOB=∠A' OB'
AB=A' B'
OC=OC'
∴ AB=A' B'
⌒
⌒
问题3:在同一个圆(简称“同圆”)或相等的圆(简称“等圆”)中
(1)如果弧相等,那么所对的圆心角,所对的弦,所对的弦心距是否相等呢?
(2)如果弦相等,那么所对的圆心角,所对的弧,所对的弦心距是否相等呢?
(3)如果弦心距相等,那么所对的圆心角,所对的弧,所对的弦是否相等呢?
?
探究发现
同圆或等圆中,如果两个圆心角相等,那么这两个圆心角所夹的两条弧、所对的两条弦,所对的弦心距都分别相等。
O
A
B
C
C'
A'
B'
∵∠AOB=∠A' OB'
AB=A' B'
OC=OC'
∴ AB=A' B'
⌒
⌒
探究发现
推论Ⅰ:同圆或等圆中,如果两条弧相等,那么这两条弧所对的
圆心角、所对的两条弦,所对的弦心距都分别相等。
推论Ⅲ:同圆或等圆中,如果两条弦心距相等,那么它们所对的
圆心角、所对的两条弦,所对的弧都分别相等。
推论Ⅱ:同圆或等圆中,如果两条弦相等,那么这两条弦所对的
圆心角、所对的两条弧,所对的弦心距都分别相等。
同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组两量相等,那么它们所对的其余各组量都分别相等。
注意:该关系定理(即圆心角定理及推论)是一种证明线段、角、弧相等的方法,当需要证明弧相等时,长常常是找到其在同圆中所对的圆心角或弦相等。
学以致用
?
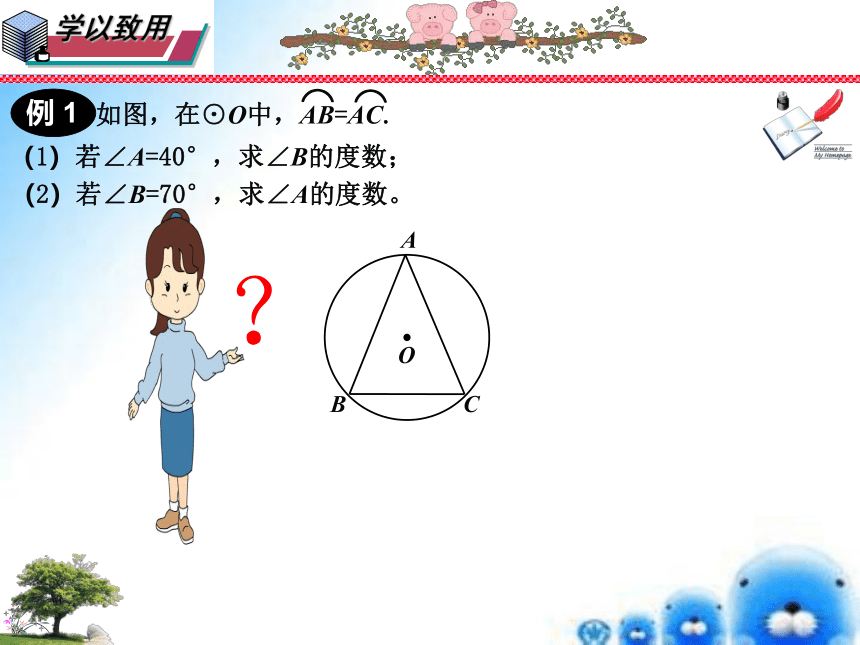
(1)若∠A=40°,求∠B的度数;
⌒
例 1
如图,在⊙O中,AB=AC.
⌒
B
A
C
O
(2)若∠B=70°,求∠A的度数。
数 学 活 动 室
学 以 致 用
C
A、40° B、60° C、80° D、120°
1.如图1,AB是⊙O的直径,C、D是BE的三等分点,∠AOE=60°,
则∠COE的度数是( )
(
2.如图2,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD
=DA,则∠BCD的度数是( )
A、100° B、110° C、120° D、135°
O
A
B
C
D
E
图1
O
A
B
C
D
图2
C
学以致用
?
例 2
如图,AB、CD是⊙O中的两条相交弦,且AB=CD,求证:AD=CB.
(
(
A
B
C
D
O
B
A
C
D
O
E
【变式】如图,AB、CD是⊙O的两条直径,弦CE//AB,求证:BC=AE.
(
(
AD=BC
学以致用
例 3
(1)求证:BM=CM;
如图,正方形ABCD内接于⊙O,M为AD的中点,连结BM、CM.
(
(2)当⊙O的半径为2时,求BM的长。
(
A
B
O
C
D
M
数 学 活 动 室
学 以 致 用
1.如图,已知OA、OB、OC是⊙O的三条半径,点C是AB的中点,
D、E分别是OA、OB的中点,求证:DC=EC
(
D
E
A
C
B
O
O
A
B
D
E
C
(
2.如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一
点,CD=CE.
(
(1)求证:AC=BC;
(2)若∠AOB=120°,CD= ,求半径OA的长。
学以致用
(1)求证:AB=CD;
例 4
如图1,点O是∠EPF的平分线上的一点,以点O为圆心的圆和角
的两边分别交于点A、B和C、D.
M
N
M
N
M
N
P
F
E
D
C
O
A
B
图 1
F
P
E
D
O
B
图 2
P
D
C
O
A
B
图 3
(2)若角的顶点P在圆上,如图2,其他条件不变,结论成立吗?
(3)若角的顶点P在圆内,如图3,其他条件不变,结论成立吗?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.1
P 39
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第27章 圆
情境激疑
问题1:请同学们思考并解答下列问题:
圆既是轴对称图形,又是中心对称图形,也是旋转对称图形。对称轴是过圆心的任意一条直线,对称中心和旋转中心都是圆心,旋转角度可以是任意角度。
(1)圆是对称图形吗?它有哪些对称性?
(2)能否用手中的圆演示出它的各种对称性呢?
(3)圆的对称轴是什么?对称中心和旋转中心是什么?
探究发现
O
A
B
C
C'
A'
B'
问题2:如图,将圆心角∠AOB绕圆心O旋转到∠A' OB'的位置,
你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A' OB'的位置时,显然∠AOB=∠A' OB' ,射线OA与OA'重合,OB与OB'重合。而同圆的半径相等,OA=OA' ,OB=OB' ,从而点A与A'重合,B与B'重合.
∵∠AOB=∠A' OB'
AB=A' B'
OC=OC'
∴ AB=A' B'
⌒
⌒
问题3:在同一个圆(简称“同圆”)或相等的圆(简称“等圆”)中
(1)如果弧相等,那么所对的圆心角,所对的弦,所对的弦心距是否相等呢?
(2)如果弦相等,那么所对的圆心角,所对的弧,所对的弦心距是否相等呢?
(3)如果弦心距相等,那么所对的圆心角,所对的弧,所对的弦是否相等呢?
?
探究发现
同圆或等圆中,如果两个圆心角相等,那么这两个圆心角所夹的两条弧、所对的两条弦,所对的弦心距都分别相等。
O
A
B
C
C'
A'
B'
∵∠AOB=∠A' OB'
AB=A' B'
OC=OC'
∴ AB=A' B'
⌒
⌒
探究发现
推论Ⅰ:同圆或等圆中,如果两条弧相等,那么这两条弧所对的
圆心角、所对的两条弦,所对的弦心距都分别相等。
推论Ⅲ:同圆或等圆中,如果两条弦心距相等,那么它们所对的
圆心角、所对的两条弦,所对的弧都分别相等。
推论Ⅱ:同圆或等圆中,如果两条弦相等,那么这两条弦所对的
圆心角、所对的两条弧,所对的弦心距都分别相等。
同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组两量相等,那么它们所对的其余各组量都分别相等。
注意:该关系定理(即圆心角定理及推论)是一种证明线段、角、弧相等的方法,当需要证明弧相等时,长常常是找到其在同圆中所对的圆心角或弦相等。
学以致用
?
(1)若∠A=40°,求∠B的度数;
⌒
例 1
如图,在⊙O中,AB=AC.
⌒
B
A
C
O
(2)若∠B=70°,求∠A的度数。
数 学 活 动 室
学 以 致 用
C
A、40° B、60° C、80° D、120°
1.如图1,AB是⊙O的直径,C、D是BE的三等分点,∠AOE=60°,
则∠COE的度数是( )
(
2.如图2,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD
=DA,则∠BCD的度数是( )
A、100° B、110° C、120° D、135°
O
A
B
C
D
E
图1
O
A
B
C
D
图2
C
学以致用
?
例 2
如图,AB、CD是⊙O中的两条相交弦,且AB=CD,求证:AD=CB.
(
(
A
B
C
D
O
B
A
C
D
O
E
【变式】如图,AB、CD是⊙O的两条直径,弦CE//AB,求证:BC=AE.
(
(
AD=BC
学以致用
例 3
(1)求证:BM=CM;
如图,正方形ABCD内接于⊙O,M为AD的中点,连结BM、CM.
(
(2)当⊙O的半径为2时,求BM的长。
(
A
B
O
C
D
M
数 学 活 动 室
学 以 致 用
1.如图,已知OA、OB、OC是⊙O的三条半径,点C是AB的中点,
D、E分别是OA、OB的中点,求证:DC=EC
(
D
E
A
C
B
O
O
A
B
D
E
C
(
2.如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一
点,CD=CE.
(
(1)求证:AC=BC;
(2)若∠AOB=120°,CD= ,求半径OA的长。
学以致用
(1)求证:AB=CD;
例 4
如图1,点O是∠EPF的平分线上的一点,以点O为圆心的圆和角
的两边分别交于点A、B和C、D.
M
N
M
N
M
N
P
F
E
D
C
O
A
B
图 1
F
P
E
D
O
B
图 2
P
D
C
O
A
B
图 3
(2)若角的顶点P在圆上,如图2,其他条件不变,结论成立吗?
(3)若角的顶点P在圆内,如图3,其他条件不变,结论成立吗?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.1
P 39
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
