华师大版九年级下册数学27.1.3 圆周角课件(15张PPT)
文档属性
| 名称 | 华师大版九年级下册数学27.1.3 圆周角课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
九年级(下)
新华东师大版第27章 圆
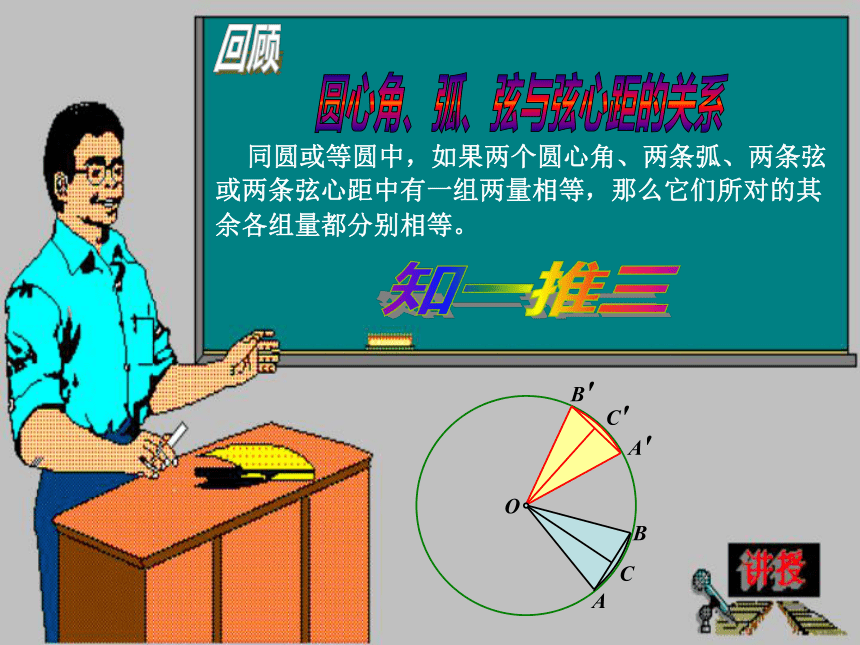
同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组两量相等,那么它们所对的其余各组量都分别相等。
O
A
B
C
C'
A'
B'
探究发现
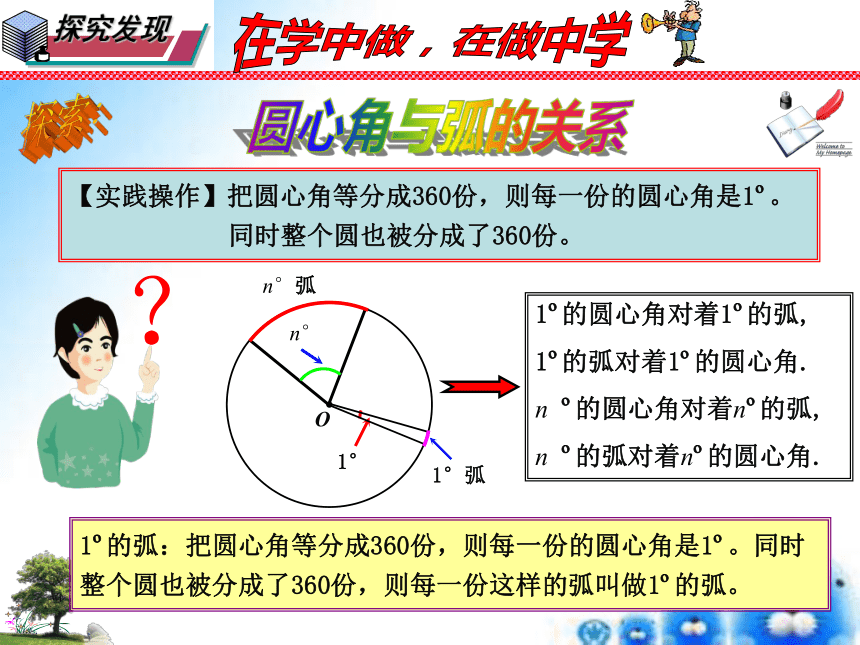
1 的弧:把圆心角等分成360份,则每一份的圆心角是1 。同时整个圆也被分成了360份,则每一份这样的弧叫做1 的弧。
?
1°弧
n°
1°
n°弧
O
1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
【实践操作】把圆心角等分成360份,则每一份的圆心角是1 。
同时整个圆也被分成了360份。
探究发现
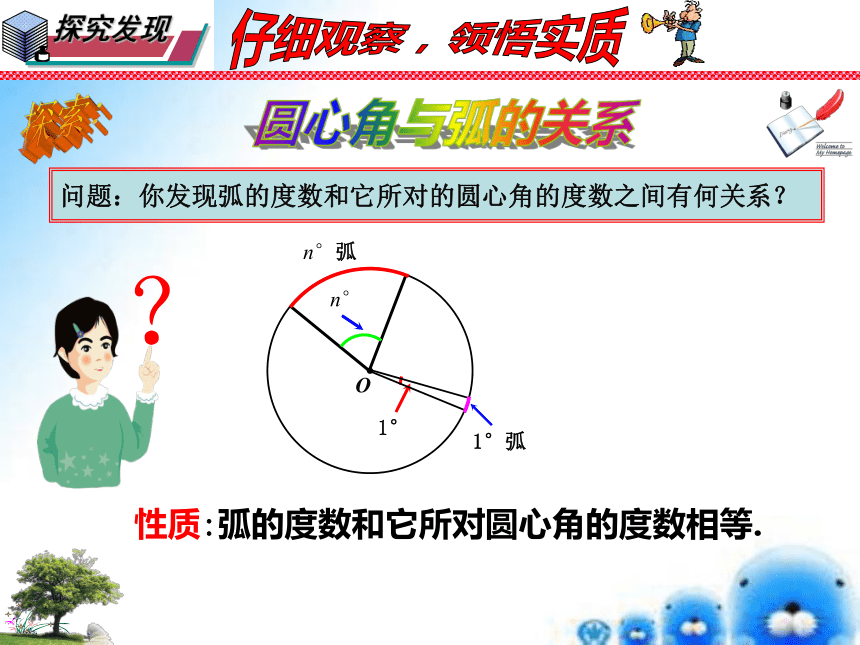
问题:你发现弧的度数和它所对的圆心角的度数之间有何关系?
?
1°弧
n°
1°
n°弧
O
性质:弧的度数和它所对圆心角的度数相等.
探究发现
(Ⅰ)1 的角:
把顶点在圆心的周角等分成360份时,每一份的圆心角是1 的角。
(Ⅱ)1 的弧:
1 的圆心角所对的弧就是1 的弧;
(或整个圆被等分成360份,每一份这样的弧就叫做1 的弧)
圆可以看作是一条360 的圆弧,它所对的圆心角是一个周角。
探究发现
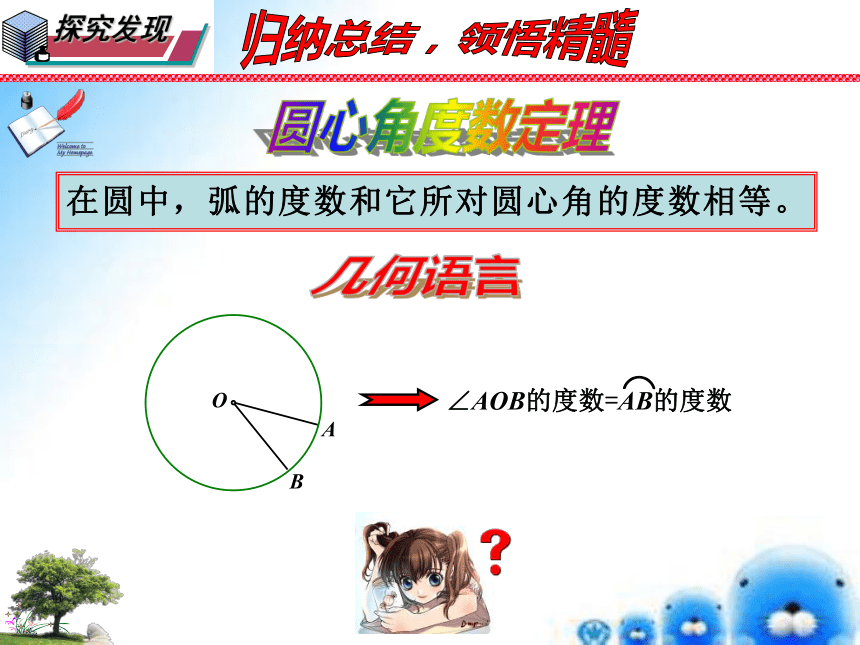
在圆中,弧的度数和它所对圆心角的度数相等。
O
A
B
∠AOB的度数=AB的度数
⌒
学以致用
?
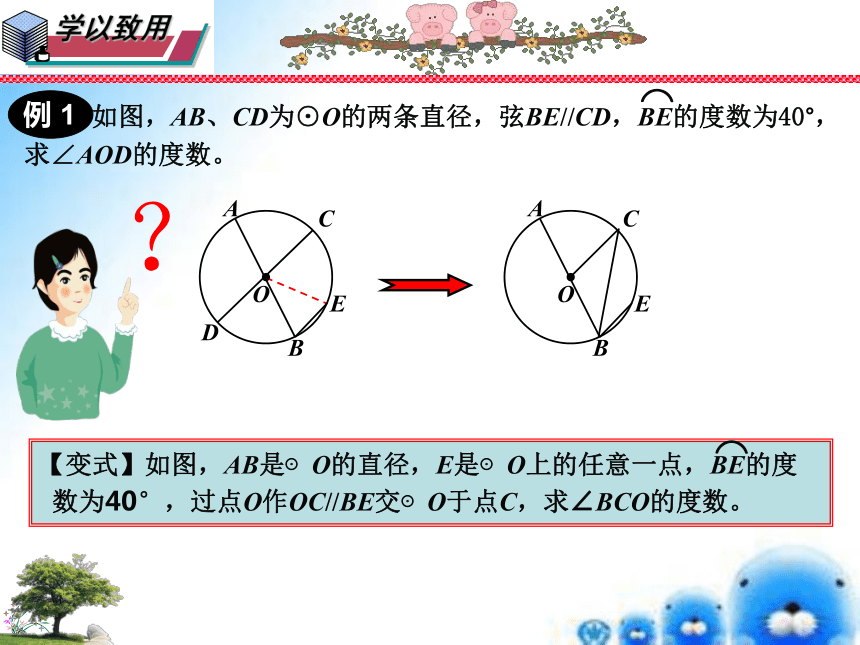
例 1
⌒
如图,AB、CD为⊙O的两条直径,弦BE//CD,BE的度数为40°,
求∠AOD的度数。
E
A
C
D
B
O
E
A
C
B
O
【变式】如图,AB是⊙O的直径,E是⊙O上的任意一点,BE的度
数为40°,过点O作OC//BE交⊙O于点C,求∠BCO的度数。
⌒
学以致用
?
例 2
如图, ⊙O中半径OA⊥OC,B是OC延长线上的一点,AB与⊙O
(
(
(1)若AD=2CD,求∠B的度数;
相交于点D.
D
A
B
C
O
(
(2)若∠B=25°,求AD所对圆心角的度数。
学以致用
例 3
如图,在⊙O中,弦AB所对的劣弧为圆的 ,圆的半径为2cm,求
AB的长。
C
A
O
B
数 学 活 动 室
学 以 致 用
1.判断下列说法是否正确.
(1)等弧的度数相等( )
(2)圆心角相等所对应的弧相等( )
(3)两条弧的长度相等,则这两条弧所对应的圆心角相等( )
×
√
×
2.已知直径为10的⊙O中,AB的度数为60°,求弦AB的弦心距。
(
数 学 活 动 室
学 以 致 用
3.如图,AB是⊙O的直径,OA⊥OC,D是CO的中点,DE//AB.
求证:CE=2AE
⌒
⌒
E
C
D
B
A
O
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.1
P 45
第2、4、5题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第27章 圆
同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中有一组两量相等,那么它们所对的其余各组量都分别相等。
O
A
B
C
C'
A'
B'
探究发现
1 的弧:把圆心角等分成360份,则每一份的圆心角是1 。同时整个圆也被分成了360份,则每一份这样的弧叫做1 的弧。
?
1°弧
n°
1°
n°弧
O
1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
【实践操作】把圆心角等分成360份,则每一份的圆心角是1 。
同时整个圆也被分成了360份。
探究发现
问题:你发现弧的度数和它所对的圆心角的度数之间有何关系?
?
1°弧
n°
1°
n°弧
O
性质:弧的度数和它所对圆心角的度数相等.
探究发现
(Ⅰ)1 的角:
把顶点在圆心的周角等分成360份时,每一份的圆心角是1 的角。
(Ⅱ)1 的弧:
1 的圆心角所对的弧就是1 的弧;
(或整个圆被等分成360份,每一份这样的弧就叫做1 的弧)
圆可以看作是一条360 的圆弧,它所对的圆心角是一个周角。
探究发现
在圆中,弧的度数和它所对圆心角的度数相等。
O
A
B
∠AOB的度数=AB的度数
⌒
学以致用
?
例 1
⌒
如图,AB、CD为⊙O的两条直径,弦BE//CD,BE的度数为40°,
求∠AOD的度数。
E
A
C
D
B
O
E
A
C
B
O
【变式】如图,AB是⊙O的直径,E是⊙O上的任意一点,BE的度
数为40°,过点O作OC//BE交⊙O于点C,求∠BCO的度数。
⌒
学以致用
?
例 2
如图, ⊙O中半径OA⊥OC,B是OC延长线上的一点,AB与⊙O
(
(
(1)若AD=2CD,求∠B的度数;
相交于点D.
D
A
B
C
O
(
(2)若∠B=25°,求AD所对圆心角的度数。
学以致用
例 3
如图,在⊙O中,弦AB所对的劣弧为圆的 ,圆的半径为2cm,求
AB的长。
C
A
O
B
数 学 活 动 室
学 以 致 用
1.判断下列说法是否正确.
(1)等弧的度数相等( )
(2)圆心角相等所对应的弧相等( )
(3)两条弧的长度相等,则这两条弧所对应的圆心角相等( )
×
√
×
2.已知直径为10的⊙O中,AB的度数为60°,求弦AB的弦心距。
(
数 学 活 动 室
学 以 致 用
3.如图,AB是⊙O的直径,OA⊥OC,D是CO的中点,DE//AB.
求证:CE=2AE
⌒
⌒
E
C
D
B
A
O
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.1
P 45
第2、4、5题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
