九年级数学(华师大版) 27.2.1 点和圆的位置关系(共26张)
文档属性
| 名称 | 九年级数学(华师大版) 27.2.1 点和圆的位置关系(共26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:32:56 | ||
图片预览


文档简介
(共26张PPT)
九年级(下)
新华东师大版第27章 圆
情境激疑
问题:一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须满足几个条件?
探究发现
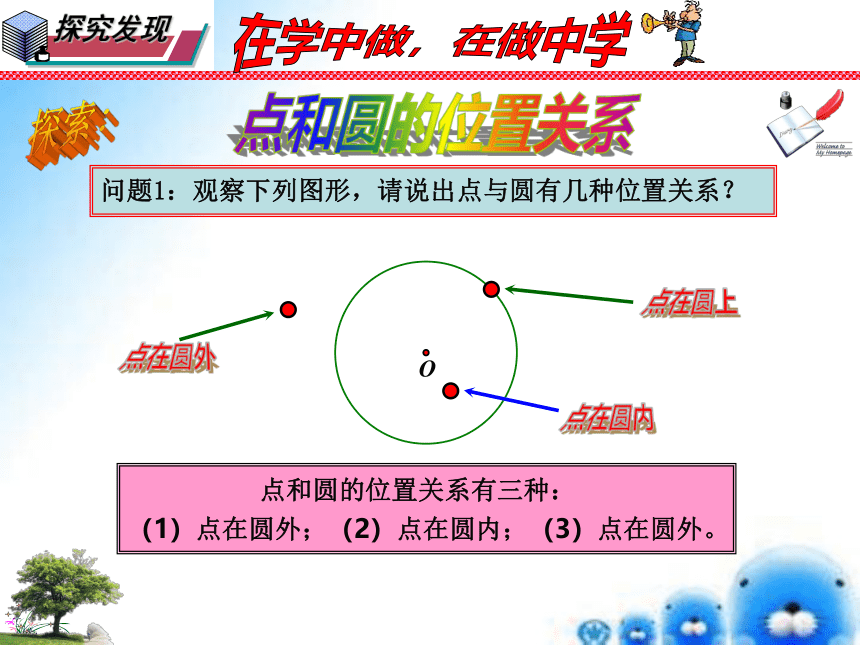
问题1:观察下列图形,请说出点与圆有几种位置关系?
O
点和圆的位置关系有三种:
(1)点在圆外;(2)点在圆内;(3)点在圆外。
探究发现
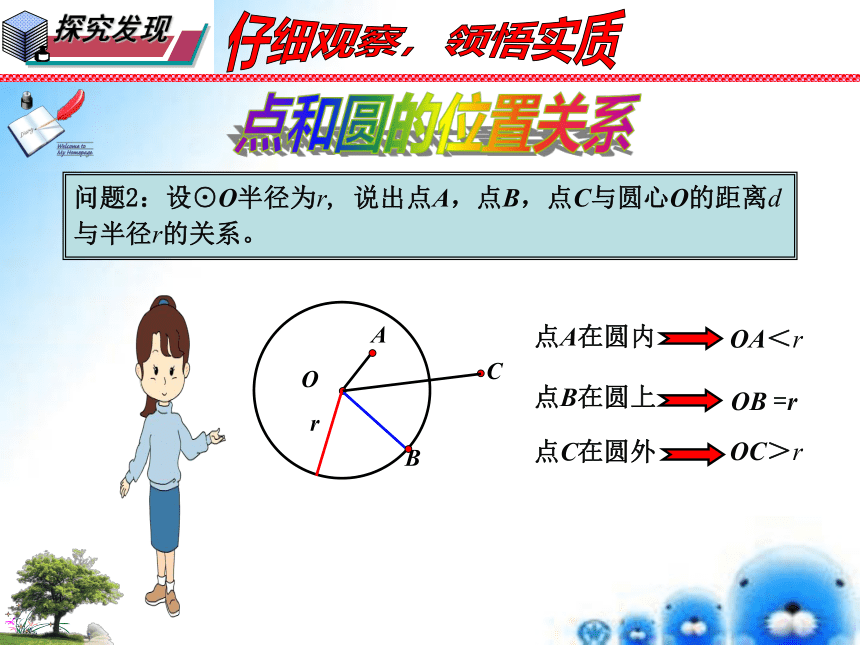
问题2:设⊙O半径为r, 说出点A,点B,点C与圆心O的距离d与半径r的关系。
r
·
C
O
A
B
OC>r
OA<r
OB =r
点C在圆外
点A在圆内
点B在圆上
探究发现
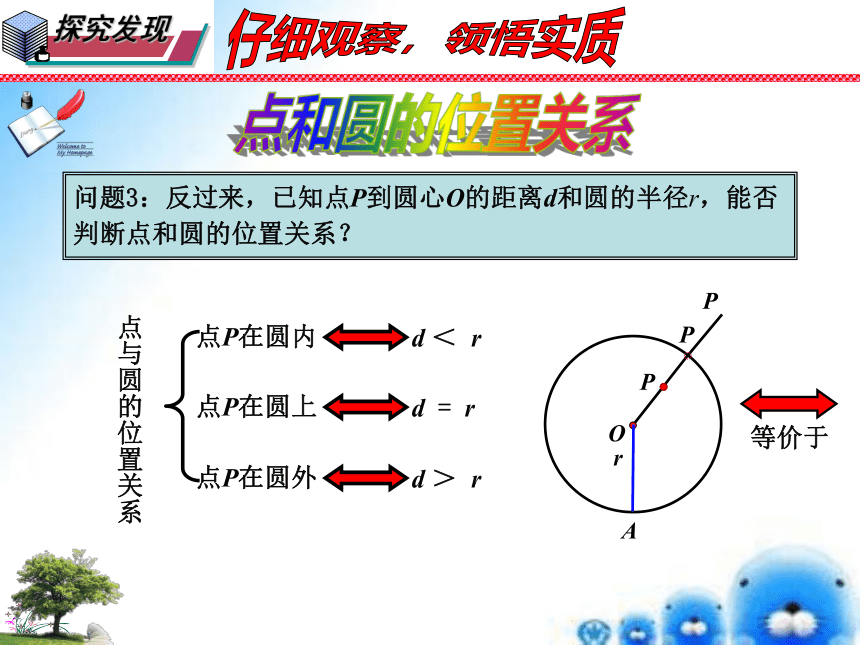
问题3:反过来,已知点P到圆心O的距离d和圆的半径r,能否判断点和圆的位置关系?
r
·
O
A
P
P
P
点P在圆内
d < r
等价于
点P在圆上
d = r
点P在圆外
d > r
点与圆的位置关系
探究发现
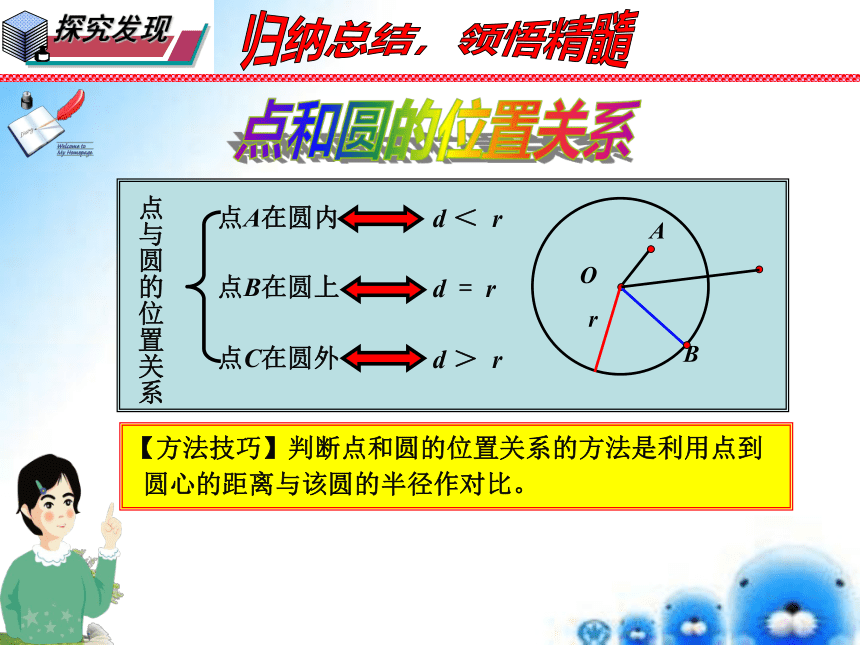
【方法技巧】判断点和圆的位置关系的方法是利用点到
圆心的距离与该圆的半径作对比。
点A在圆内
d < r
点B在圆上
d = r
点C在圆外
d > r
点与圆的位置关系
r
·
O
A
B
学以致用
例 1
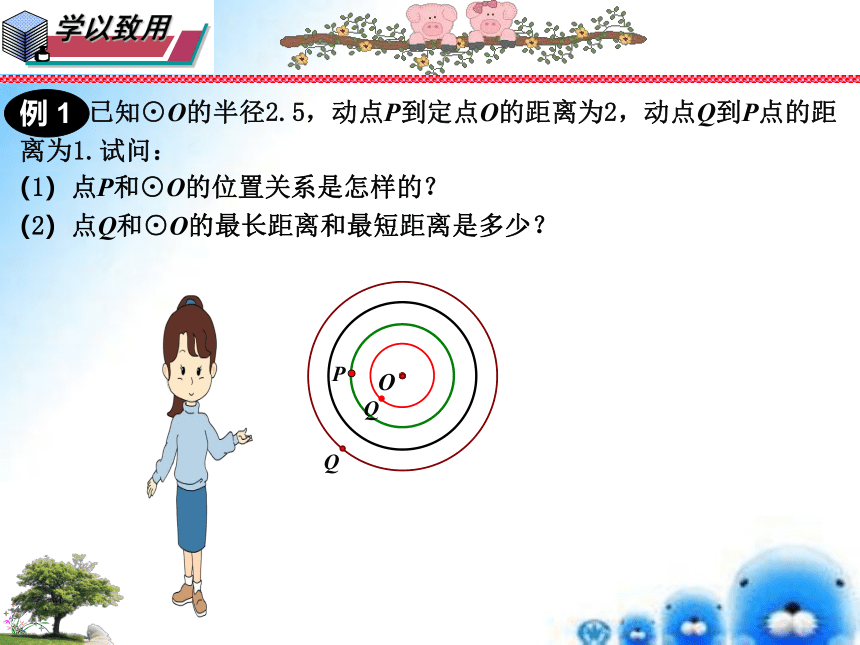
已知⊙O的半径2.5,动点P到定点O的距离为2,动点Q到P点的距
离为1.试问:
O
P
Q
Q
(1)点P和⊙O的位置关系是怎样的?
(2)点Q和⊙O的最长距离和最短距离是多少?
数 学 活 动 室
学 以 致 用
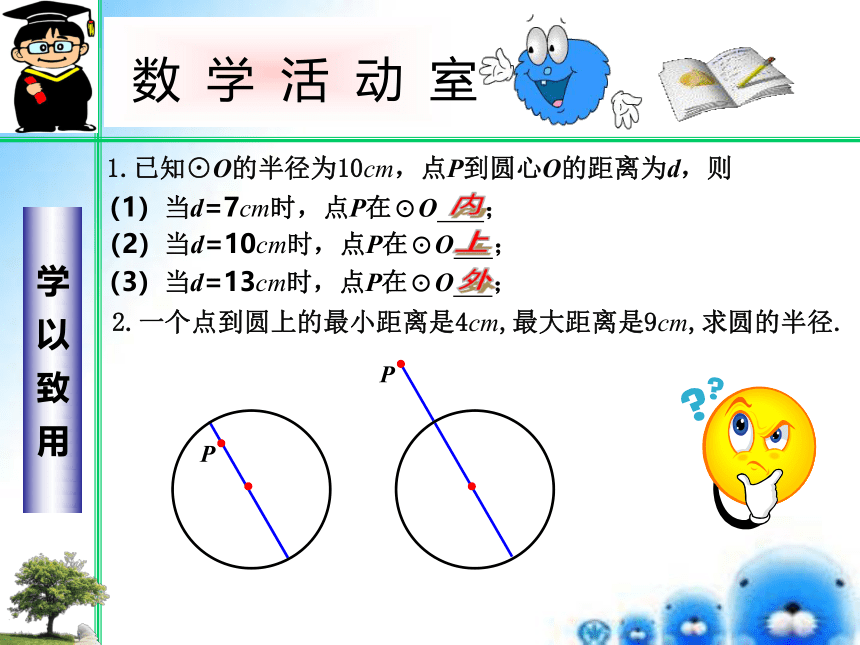
1.已知⊙O的半径为10cm,点P到圆心O的距离为d,则
2.一个点到圆上的最小距离是4cm,最大距离是9cm,求圆的半径.
P
P
(1)当d=7cm时,点P在⊙O ;
(2)当d=10cm时,点P在⊙O ;
(3)当d=13cm时,点P在⊙O ;
学以致用
例 2
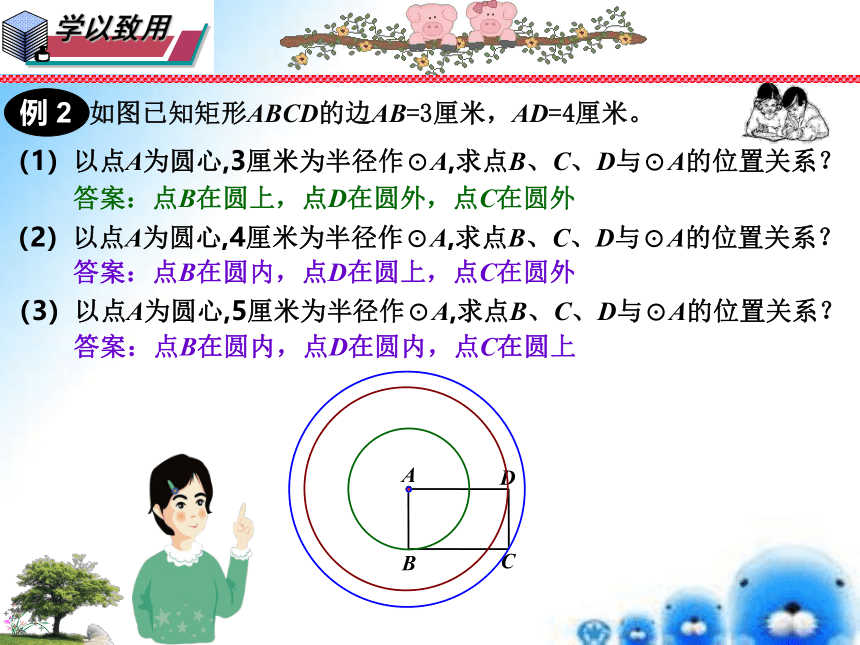
如图已知矩形ABCD的边AB=3厘米,AD=4厘米。
A
D
C
B
(1)以点A为圆心,3厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆上,点D在圆外,点C在圆外
(2)以点A为圆心,4厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆内,点D在圆上,点C在圆外
(3)以点A为圆心,5厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆内,点D在圆内,点C在圆上
数 学 活 动 室
学 以 致 用
2.在Rt△ABC中,∠C=90°,BC=3厘米,AC=4厘米。
C
A
B
D
(1)以点C为圆心,3厘米为半径作⊙C,求点A、B与⊙A的位置?
(2)以点C为圆心,4厘米为半径作⊙C,求点A、B与⊙A的位置?
(3)以点C为圆心,5厘米为半径作⊙C,求点A、B与⊙A的位置?
学以致用
例 3
如图,AC⊥AB于A,BD⊥DC于D.
求证:A、B、C、D四个点在同一个圆上。
【方法归纳】证明多点共圆的方法就是证明这些点到同一个定点
的距离固定不变即可。
A
B
C
D
O
A
B
C
D
O
探究发现
过几点可以确定一个圆呢?
探究发现
问题4:经过一个已知点A你可以确定圆吗?你会怎么画这个圆?
【探究报告1】经过一个已知点能做无数个圆。
A
探究发现
问题5:经过两个已知点A、B能确定一个圆吗?你会怎样画圆?
A
B
【探究报告2】经过已知两点能作无数个圆。
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的中垂线上
探究发现
问题6:经过三个已知点A、B、C能确定一个圆吗?你是怎样考虑的?
A
B
C
过如下三点能不能做圆 为什么
【探究报告3】经过同一直线上的三点不能作圆。
探究发现
问题6:经过三个已知点A、B、C能确定一个圆吗?你是怎样考虑的?
F
E
A
B
C
M
N
O
(1)过如下三点能不能作圆?若能,如何确定圆心和半径?
(2)请你尺规作图作经过A、B、C三点的圆;
(3)经过不在同一条直线上的三点可以作几个圆?
探究发现
定理:不在同一条直线上的三个点确定一个圆。
A
B
C
O
一个三角形的外接圆有且只有一个,一个圆的内接三角形有无数个。
(1)经过三角形三个顶点的圆叫做三角形的外接圆;
(2)三角形外接圆的圆心叫做三角形的外心;
(3)这个三角形叫做圆的内接三角形;
(4)三角形的外心就是三角形三边垂直平分线的交点,外心到三角
形三个顶点的距离相等。
探究发现
问题7:请同学们分别作出一个锐角三角形、直角三角形、钝角三角形并画出它的外接圆,观察外心的位置,你能得到什么结论?
A
B
C
A
B
C
A
B
C
O
O
O
(1)锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角
形斜边中点,钝角三角形的外心位于三角形外;
(2)直角三角形的外心是斜边的中点。
学以致用
问题:一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
A
B
C
O
若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该圆片的半径。
学以致用
例 4
如图,△ABC是等腰三角形,BC=16cm,AB=AC=10cm.
求△ABC外接圆的半径。
B
C
A
O
D
A
B
C
D
O
13
10
A
B
C
D
O
10
B
A
C
5
12
学以致用
?
例 5
如图,在△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,
求∠BOC的度数。
C
A
B
O
A
C
B
O
【变式】如图,⊙O是△ABC的外接圆,已知∠B=60°,求∠BOC的度数.
数 学 活 动 室
经 典 数 学
1.在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC
外接圆半径。
A
B
C
D
O
2.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0
的两根,求Rt△ABC的外接圆面积。
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.2
P 55
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第27章 圆
情境激疑
问题:一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须满足几个条件?
探究发现
问题1:观察下列图形,请说出点与圆有几种位置关系?
O
点和圆的位置关系有三种:
(1)点在圆外;(2)点在圆内;(3)点在圆外。
探究发现
问题2:设⊙O半径为r, 说出点A,点B,点C与圆心O的距离d与半径r的关系。
r
·
C
O
A
B
OC>r
OA<r
OB =r
点C在圆外
点A在圆内
点B在圆上
探究发现
问题3:反过来,已知点P到圆心O的距离d和圆的半径r,能否判断点和圆的位置关系?
r
·
O
A
P
P
P
点P在圆内
d < r
等价于
点P在圆上
d = r
点P在圆外
d > r
点与圆的位置关系
探究发现
【方法技巧】判断点和圆的位置关系的方法是利用点到
圆心的距离与该圆的半径作对比。
点A在圆内
d < r
点B在圆上
d = r
点C在圆外
d > r
点与圆的位置关系
r
·
O
A
B
学以致用
例 1
已知⊙O的半径2.5,动点P到定点O的距离为2,动点Q到P点的距
离为1.试问:
O
P
Q
Q
(1)点P和⊙O的位置关系是怎样的?
(2)点Q和⊙O的最长距离和最短距离是多少?
数 学 活 动 室
学 以 致 用
1.已知⊙O的半径为10cm,点P到圆心O的距离为d,则
2.一个点到圆上的最小距离是4cm,最大距离是9cm,求圆的半径.
P
P
(1)当d=7cm时,点P在⊙O ;
(2)当d=10cm时,点P在⊙O ;
(3)当d=13cm时,点P在⊙O ;
学以致用
例 2
如图已知矩形ABCD的边AB=3厘米,AD=4厘米。
A
D
C
B
(1)以点A为圆心,3厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆上,点D在圆外,点C在圆外
(2)以点A为圆心,4厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆内,点D在圆上,点C在圆外
(3)以点A为圆心,5厘米为半径作⊙A,求点B、C、D与⊙A的位置关系?
答案:点B在圆内,点D在圆内,点C在圆上
数 学 活 动 室
学 以 致 用
2.在Rt△ABC中,∠C=90°,BC=3厘米,AC=4厘米。
C
A
B
D
(1)以点C为圆心,3厘米为半径作⊙C,求点A、B与⊙A的位置?
(2)以点C为圆心,4厘米为半径作⊙C,求点A、B与⊙A的位置?
(3)以点C为圆心,5厘米为半径作⊙C,求点A、B与⊙A的位置?
学以致用
例 3
如图,AC⊥AB于A,BD⊥DC于D.
求证:A、B、C、D四个点在同一个圆上。
【方法归纳】证明多点共圆的方法就是证明这些点到同一个定点
的距离固定不变即可。
A
B
C
D
O
A
B
C
D
O
探究发现
过几点可以确定一个圆呢?
探究发现
问题4:经过一个已知点A你可以确定圆吗?你会怎么画这个圆?
【探究报告1】经过一个已知点能做无数个圆。
A
探究发现
问题5:经过两个已知点A、B能确定一个圆吗?你会怎样画圆?
A
B
【探究报告2】经过已知两点能作无数个圆。
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的中垂线上
探究发现
问题6:经过三个已知点A、B、C能确定一个圆吗?你是怎样考虑的?
A
B
C
过如下三点能不能做圆 为什么
【探究报告3】经过同一直线上的三点不能作圆。
探究发现
问题6:经过三个已知点A、B、C能确定一个圆吗?你是怎样考虑的?
F
E
A
B
C
M
N
O
(1)过如下三点能不能作圆?若能,如何确定圆心和半径?
(2)请你尺规作图作经过A、B、C三点的圆;
(3)经过不在同一条直线上的三点可以作几个圆?
探究发现
定理:不在同一条直线上的三个点确定一个圆。
A
B
C
O
一个三角形的外接圆有且只有一个,一个圆的内接三角形有无数个。
(1)经过三角形三个顶点的圆叫做三角形的外接圆;
(2)三角形外接圆的圆心叫做三角形的外心;
(3)这个三角形叫做圆的内接三角形;
(4)三角形的外心就是三角形三边垂直平分线的交点,外心到三角
形三个顶点的距离相等。
探究发现
问题7:请同学们分别作出一个锐角三角形、直角三角形、钝角三角形并画出它的外接圆,观察外心的位置,你能得到什么结论?
A
B
C
A
B
C
A
B
C
O
O
O
(1)锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角
形斜边中点,钝角三角形的外心位于三角形外;
(2)直角三角形的外心是斜边的中点。
学以致用
问题:一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
A
B
C
O
若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该圆片的半径。
学以致用
例 4
如图,△ABC是等腰三角形,BC=16cm,AB=AC=10cm.
求△ABC外接圆的半径。
B
C
A
O
D
A
B
C
D
O
13
10
A
B
C
D
O
10
B
A
C
5
12
学以致用
?
例 5
如图,在△ABC中,AB=AC,∠ABC=70°,点O是△ABC的外心,
求∠BOC的度数。
C
A
B
O
A
C
B
O
【变式】如图,⊙O是△ABC的外接圆,已知∠B=60°,求∠BOC的度数.
数 学 活 动 室
经 典 数 学
1.在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC
外接圆半径。
A
B
C
D
O
2.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0
的两根,求Rt△ABC的外接圆面积。
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 27.2
P 55
第1、2、3题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
