九年级下册数学华师大版27.2与圆有关的位置关系 本节综合与测试 ---圆与圆的位置关系(共25张)
文档属性
| 名称 | 九年级下册数学华师大版27.2与圆有关的位置关系 本节综合与测试 ---圆与圆的位置关系(共25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:37:11 | ||
图片预览





文档简介
(共25张PPT)
九年级(下)
新华东师大版第27章 圆
温故知新
(Ⅰ)点和圆的位置关系:
A
O
B
C
d
d
R
d
(Ⅱ)直线和圆的位置关系:
探究发现
问题1:请你认真观察两圆的运动过程,注意两圆的位置关系。
探究发现
下面有许多圆,用鼠标指着圆心,按下左键就能将圆放到你想要的位置,请你根据刚才的观察,摆出心中两圆的各种位置关系。
探究发现
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
探究发现
问题2:设两圆的半径分别为R、r,圆心距为d,你能利用两圆的半径R、r及圆心距d判断两圆的位置关系吗?
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
探究发现
问题2:设两圆的半径分别为R、r,圆心距为d,你能利用两圆的半径R、r及圆心距d判断两圆的位置关系吗?
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
R+r<d
R+r=d
R-r<d<R+r
R-r=d
R-r>d
探究发现
两圆的位置关系 公共点个数 数量关系及其判定方法
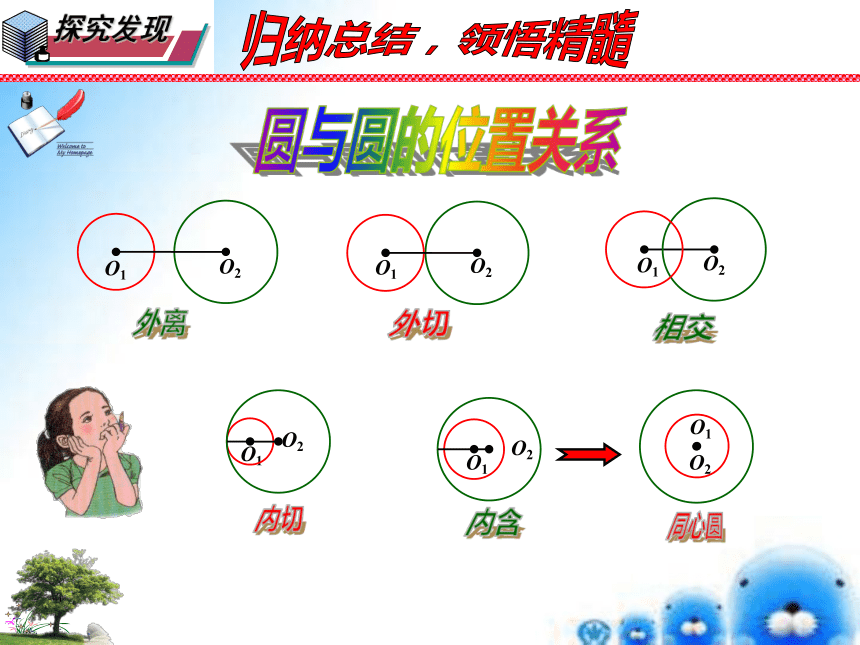
外离
外切
相交
内切
内含
探究发现
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
0
R-r
R+r
探究发现
问题3:圆是轴对称图形,两个圆是否也组成轴对称图形呢?如果能组成轴对称图形,那么对称轴是什么?
探究发现
(Ⅰ)两个圆一定组成轴对称图形,对称轴是两圆的连心线;
(Ⅱ)相切两圆的性质:相切两圆的连心线必过切点;
(Ⅲ)相交两圆的性质:相交两圆的连心线垂直平分公共弦。
学以致用
例 1
已知⊙A、⊙B相切,圆心距为10cm,其中⊙A的半径为4cm,求
【变式】已知⊙A、⊙B的圆心距为10cm,其中⊙A的半径为4cm.
(1)当⊙A、⊙B外离时,求⊙B的半径取值范围;
(2)当⊙A、⊙B相交时,求⊙B的半径取值范围;
(3)当⊙A、⊙B内含时,求⊙B的半径取值范围。
⊙B的半径。
A
外切
B
内切
B
A
学以致用
例 2
已知⊙O1与⊙O2的半径分别为R、r,且R≥r,R、r是
的两根,设O1O2=d.
(1)若d=5.5,试判断⊙O1与⊙O2的位置关系;
(2)若d=3,试判断⊙O1与⊙O2的位置关系;
(3)若d=4.5,试判断⊙O1与⊙O2的位置关系。
【同步】已知两圆的半径分别为3和7,且这两个圆有公共点,求
这两个圆的圆心距d取值范围。
数 学 活 动 室
学 以 致 用
1.如图,⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,求
B
P
O
(1)已点P为圆心,作⊙P与⊙O外切,求小圆P的半径;
(2)已点P为圆心,作⊙P与⊙O内切,求大圆P的半径。
学以致用
(1)试问O1A与O2B有怎样的位置关系?证明你的结论;
例 3
如图,⊙O1与⊙O2外切于点P,过P点作直线交⊙O1、⊙O2于A、B,
(2)若将⊙O1与⊙O2外切于点P改为内切于点P,(1)的结论是否仍成
立?证明你的结论。
连结O1A、O2B.
A
O1
P
B
O2
P
A
B
O2
O1
数 学 活 动 室
学 以 致 用
3.如图,⊙O1与⊙O2外切于点P,过P点作直线交⊙O1、⊙O2于A、B,∠AO1P=80°,点C是⊙O2上任意一点,求∠PCB的度数。
C
P
A
B
O2
O1
学以致用
例 4
已知⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径
为17,公共弦AB=16,求两圆的圆心距。
C
A
B
O2
O1
C
B
A
O2
O1
【变式】已知两圆的半径分别是15和13,当公共弦取得最大值时,求此时
圆心距为多少?
?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第27章 圆
温故知新
(Ⅰ)点和圆的位置关系:
A
O
B
C
d
d
R
d
(Ⅱ)直线和圆的位置关系:
探究发现
问题1:请你认真观察两圆的运动过程,注意两圆的位置关系。
探究发现
下面有许多圆,用鼠标指着圆心,按下左键就能将圆放到你想要的位置,请你根据刚才的观察,摆出心中两圆的各种位置关系。
探究发现
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
O1
O2
探究发现
问题2:设两圆的半径分别为R、r,圆心距为d,你能利用两圆的半径R、r及圆心距d判断两圆的位置关系吗?
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
探究发现
问题2:设两圆的半径分别为R、r,圆心距为d,你能利用两圆的半径R、r及圆心距d判断两圆的位置关系吗?
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
R+r<d
R+r=d
R-r<d<R+r
R-r=d
R-r>d
探究发现
两圆的位置关系 公共点个数 数量关系及其判定方法
外离
外切
相交
内切
内含
探究发现
O1
外离
O2
r
d
R
O1
外切
O2
r
d
R
O1
相交
O2
r
d
R
r
内切
O1
O2
d
R
r
d
O1
内含
O2
R
0
R-r
R+r
探究发现
问题3:圆是轴对称图形,两个圆是否也组成轴对称图形呢?如果能组成轴对称图形,那么对称轴是什么?
探究发现
(Ⅰ)两个圆一定组成轴对称图形,对称轴是两圆的连心线;
(Ⅱ)相切两圆的性质:相切两圆的连心线必过切点;
(Ⅲ)相交两圆的性质:相交两圆的连心线垂直平分公共弦。
学以致用
例 1
已知⊙A、⊙B相切,圆心距为10cm,其中⊙A的半径为4cm,求
【变式】已知⊙A、⊙B的圆心距为10cm,其中⊙A的半径为4cm.
(1)当⊙A、⊙B外离时,求⊙B的半径取值范围;
(2)当⊙A、⊙B相交时,求⊙B的半径取值范围;
(3)当⊙A、⊙B内含时,求⊙B的半径取值范围。
⊙B的半径。
A
外切
B
内切
B
A
学以致用
例 2
已知⊙O1与⊙O2的半径分别为R、r,且R≥r,R、r是
的两根,设O1O2=d.
(1)若d=5.5,试判断⊙O1与⊙O2的位置关系;
(2)若d=3,试判断⊙O1与⊙O2的位置关系;
(3)若d=4.5,试判断⊙O1与⊙O2的位置关系。
【同步】已知两圆的半径分别为3和7,且这两个圆有公共点,求
这两个圆的圆心距d取值范围。
数 学 活 动 室
学 以 致 用
1.如图,⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,求
B
P
O
(1)已点P为圆心,作⊙P与⊙O外切,求小圆P的半径;
(2)已点P为圆心,作⊙P与⊙O内切,求大圆P的半径。
学以致用
(1)试问O1A与O2B有怎样的位置关系?证明你的结论;
例 3
如图,⊙O1与⊙O2外切于点P,过P点作直线交⊙O1、⊙O2于A、B,
(2)若将⊙O1与⊙O2外切于点P改为内切于点P,(1)的结论是否仍成
立?证明你的结论。
连结O1A、O2B.
A
O1
P
B
O2
P
A
B
O2
O1
数 学 活 动 室
学 以 致 用
3.如图,⊙O1与⊙O2外切于点P,过P点作直线交⊙O1、⊙O2于A、B,∠AO1P=80°,点C是⊙O2上任意一点,求∠PCB的度数。
C
P
A
B
O2
O1
学以致用
例 4
已知⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径
为17,公共弦AB=16,求两圆的圆心距。
C
A
B
O2
O1
C
B
A
O2
O1
【变式】已知两圆的半径分别是15和13,当公共弦取得最大值时,求此时
圆心距为多少?
?
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
