九年级下册数学(华师大版) 27.3 圆中的计算问题--- 弧长和扇形的面积(共33张)
文档属性
| 名称 | 九年级下册数学(华师大版) 27.3 圆中的计算问题--- 弧长和扇形的面积(共33张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 20:48:30 | ||
图片预览










文档简介
(共33张PPT)
九年级(下)
新华东师大版第27章 圆
温故知新
(Ⅰ)圆的周长公式:
(Ⅱ)圆的面积公式:
情境激疑
问题:如图是圆弧形状的铁轨示意图,其中铁轨的半径100m,圆心
角为90°,你能求出这段铁轨的长度吗?
如果圆心角是任意角度,如何计算它所对的弧长呢?
我们容易看出这段铁轨是圆周长的
故铁轨的长度为:
探究发现
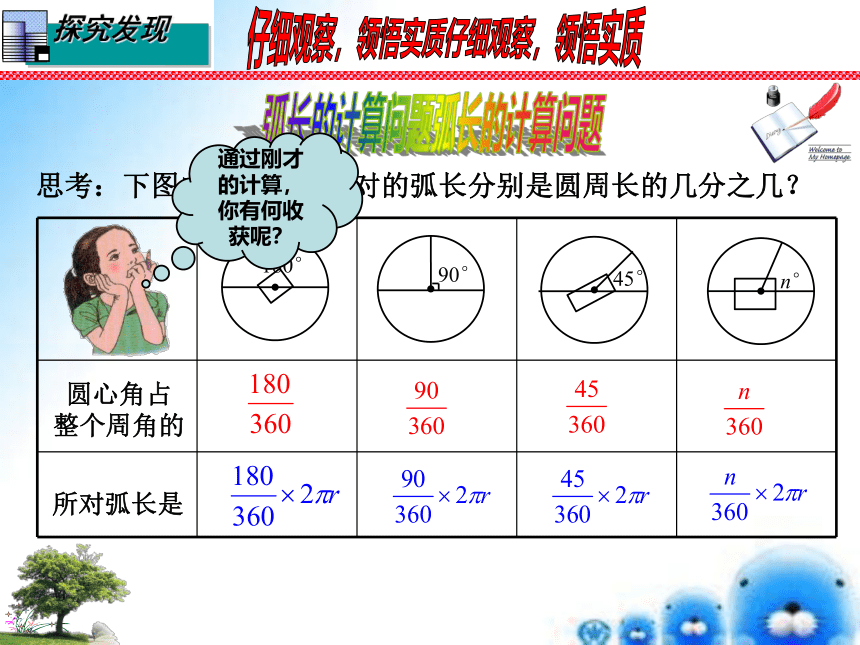
思考:下图中各圆心角所对的弧长分别是圆周长的几分之几?
90°
45°
n°
180°
圆心角占
整个周角的
所对弧长是
通过刚才的计算,你有何收获呢?
探究发现
思考:如果弧长为l,圆心角的度数为n,圆的半径为r,那么
探究发现
(1)在弧长公式中,n表示“1°”的圆心角的倍数,在应用公式计算
时,“n”和“180”可不写单位;
如果弧长为l,圆心角度数为n,圆的半径为r,那么,
弧长的计算公式为:
(2)若题目中没有标明精确度,可以用“ ”表示弧长;
(3)要正确区分弧、弧的度数、弧长三个概念:度数相等的弧,弧长
不一定相等,弧长相等的弧也不一定是等弧.要充分注意:只有
在同圆或等圆中,才可能是等弧,才有这三者的统一。
学以致用
【方法点拨】在弧长公式中有三个未知量:弧长、半径、圆心角的度数,
利用弧长公式可解决已知这三个量中的两个量求第三个量的问题。
例 1
若扇形的半径为6,圆心角为120°,则此时扇形的弧长是( )
A、 B、 C、 D、
B
数 学 活 动 室
学 以 致 用
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
( )
A、 B、 C、 D、
A、 B、 C、 D、
2.如图,四边形ABCD是⊙O的内接四边形, ⊙O的半径为2,
∠B=135°,则ABC的长为( )
C
C
O
A
B
C
D
学以致用
例 2
如图,已知⊙O半径为6cm,直线AB是⊙O的切线,切点为点B,弦
BC//AO,若∠A=30°,求劣弧BC的长。
B
C
A
O
数 学 活 动 室
学 以 致 用
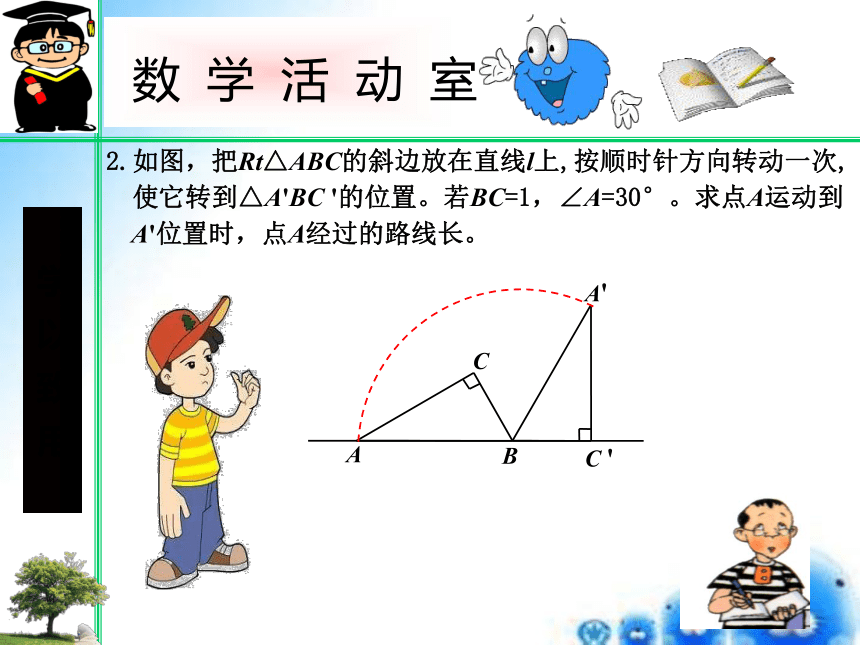
2.如图,把Rt△ABC的斜边放在直线l上,按顺时针方向转动一次,
使它转到△A'BC '的位置。若BC=1,∠A=30°。求点A运动到
A'位置时,点A经过的路线长。
C
A
B
C '
A'
数 学 活 动 室
学 以 致 用
3.如图,⊙O1的半径是⊙O2的直径,C是⊙O1上的一点,O1C交⊙O2于点B,若⊙O1的半径为5cm,AC的长等于⊙O1周长的 ,
求AB的长。
B
A
O1
O2
C
学以致用
【方法点拨】求弧长需要的两个条件:(1)弧所在圆的半径;(2)弧
所对的圆心角。当题中没有直接给出这两个条件时,则需利用圆的相关
知识:弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角.
例 3
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD
的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF= 米,则这段弯路的长度为( )
A、 米 B、 米
C、 米 D、 米
D
E
C
O
F
A
数 学 活 动 室
经 典 数 学
4.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
数 学 活 动 室
经 典 数 学
5.秋千拉绳长3m,静止时踩板离地面0.5m。某小朋友荡秋千时,秋千在最高处踩板距地面2m(左右对称),如图,则该秋千荡过的圆弧长为( )
A、 B、 C、 D、
O
F
A
B
E
D
B
学以致用
扇形:如图,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形。
O
A
B
n°
l
r
r
探究发现
思考:下图中各扇形面积分别是圆面积的几分之几?
90°
45°
n°
180°
圆心角占
整个周角的
扇形面积
通过刚才的计算,你有何收获呢?
探究发现
如果设圆心角是n的扇形面积为S,圆的半径为r,那么扇形的面积为:
A
B
O
O
180
R
n
l
p
=
探究发现
若设圆心角是n的扇形面积为S,圆的半径为r,则扇形的面积为:
探究发现
(Ⅰ)应用方法:
(Ⅱ)特别注意:
(1)当已知半径r和圆心角求扇形面积时,选用公式
(2)当已知半径r和弧长求扇形的面积时,选用公式
(1)已知S,l,n,r四个量中的任意两个量,可以求出另外两个量;
(2)在扇形公式 中,n,360不带单位。
学以致用
例 4
如图,在□ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分
?
的面积是( )
C
A
B
C
D
A、 B、 C、 D、
【变式】如图,分别以□ABCD四个顶点为圆心,1cm为半径作⊙A、⊙B、
⊙C 、⊙D,求图中阴影部分的面积之和。
A
B
D
C
学以致用
例 5
如图,分别以△ABC三个顶点为圆心,1cm为半径作⊙A、⊙B、⊙C
求图中阴影部分的面积之和。
A
B
B
B
A
C
【拓展】如图,依次以三角形、四边形、……、n边形的各顶点为圆心画
半径为1的圆,且圆与圆之间两两不相交。把三角形与各圆重叠部分面积
之和记为S3,四边形与各圆重叠部分面积之和记为S4, ……,n边形与各圆
重叠部分面积之和记为Sn,求S90的值。
A
B
C
D
数 学 活 动 室
学 以 致 用
1.已知扇形的圆心角为120°,半径为2,求这个扇形的面积;
2.已知扇形面积为 ,圆心角为60°,求这个扇形的半径R;
3.已知半径为2cm的扇形,其弧长为 ,求这个扇形的面积。
4.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇
形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴
纸部分的面积为( )
A、 B、 C、 D、
A
C
O
B
B
学以致用
我是这样想的…
【归纳】解决由弦及其所对的弧组成的图形(即弓形)的方法是:转化
为扇形的面积与三角形的面积之差(和)。
A
例 6
如图,已知扇形AOB的半径为2,圆心角为90°,连结AB,则图中阴影
部分的面积是( )
A、 B、 C、 D、
B
A
O
数 学 活 动 室
经 典 数 学
5.如图,AB为⊙O的切线,切点为B,连结AO,AO与⊙O交于点C,
BD为⊙O的直径,连结CD.若∠A=30°,⊙O的半径为2,则图中
阴影部分的面积为( )
A、 B、
C、 D、
O
B
A
C
D
学以致用
例 7
如图,等腰直角三角形ABC中,AB=AC=8,以AB为直径的半圆O交斜
边BC于点D,求图中阴影部分的面积。
你怎样思考的?
O
C
A
D
B
【技巧】(1)本例中的阴影部分虽然不是规则图形,但它的面积可以转
化为三个规则图形的面积差,因此我们只需分别求出一个扇形面积和
两个三角形面积即可达到目的;(2)求不规则图形面积时,常采用的
方法有:①作差法;②割补法;③拼凑法;④等积变形法;⑤迁移变
换法;⑥化零为整法;⑦平移法。
学以致用
例 8
如图,两个半圆形中,长为24的弦AB与直径CD平行且与小半圆相
【注意】利用平移等图形变换可将不规则图形面积转化为规则图形面积
的和、差进行求解。
切,求图中阴影部分的面积。
B
A
C
D
O
B
A
C
D
O
E
学以致用
例 9
如图,扇形OAB与扇形OCD的圆心角均为90°,连结AC,BD.
【技巧方法】计算不规则图形的面积时,常常通过割补法将不规则图形
的面积转化为及格规则图形面积的和或差的形式。
O
A
B
D
F
C
E
(1)求证:AC=BD;
(2)若图中阴影部分的面积是 ,OA=2cm,求OC的长。
数 学 活 动 室
学 以 致 用
6.如图,已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积S.
D
C
F
E
B
A
数 学 活 动 室
学 以 致 用
7.如图,正六边形内接于⊙O,⊙O的半径为10,求图中阴影部分的面积。
O
8.如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和。
数 学 活 动 室
学 以 致 用
9.如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,O、H分别为AB、AC的中点,将△ABC顺时针旋转120°到△A1BC1的位置,求
整个旋转过程中线段OH所扫过的面积。
A
H
B
O
C
H1
O1
A1
C1
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
九年级(下)
新华东师大版第27章 圆
温故知新
(Ⅰ)圆的周长公式:
(Ⅱ)圆的面积公式:
情境激疑
问题:如图是圆弧形状的铁轨示意图,其中铁轨的半径100m,圆心
角为90°,你能求出这段铁轨的长度吗?
如果圆心角是任意角度,如何计算它所对的弧长呢?
我们容易看出这段铁轨是圆周长的
故铁轨的长度为:
探究发现
思考:下图中各圆心角所对的弧长分别是圆周长的几分之几?
90°
45°
n°
180°
圆心角占
整个周角的
所对弧长是
通过刚才的计算,你有何收获呢?
探究发现
思考:如果弧长为l,圆心角的度数为n,圆的半径为r,那么
探究发现
(1)在弧长公式中,n表示“1°”的圆心角的倍数,在应用公式计算
时,“n”和“180”可不写单位;
如果弧长为l,圆心角度数为n,圆的半径为r,那么,
弧长的计算公式为:
(2)若题目中没有标明精确度,可以用“ ”表示弧长;
(3)要正确区分弧、弧的度数、弧长三个概念:度数相等的弧,弧长
不一定相等,弧长相等的弧也不一定是等弧.要充分注意:只有
在同圆或等圆中,才可能是等弧,才有这三者的统一。
学以致用
【方法点拨】在弧长公式中有三个未知量:弧长、半径、圆心角的度数,
利用弧长公式可解决已知这三个量中的两个量求第三个量的问题。
例 1
若扇形的半径为6,圆心角为120°,则此时扇形的弧长是( )
A、 B、 C、 D、
B
数 学 活 动 室
学 以 致 用
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
( )
A、 B、 C、 D、
A、 B、 C、 D、
2.如图,四边形ABCD是⊙O的内接四边形, ⊙O的半径为2,
∠B=135°,则ABC的长为( )
C
C
O
A
B
C
D
学以致用
例 2
如图,已知⊙O半径为6cm,直线AB是⊙O的切线,切点为点B,弦
BC//AO,若∠A=30°,求劣弧BC的长。
B
C
A
O
数 学 活 动 室
学 以 致 用
2.如图,把Rt△ABC的斜边放在直线l上,按顺时针方向转动一次,
使它转到△A'BC '的位置。若BC=1,∠A=30°。求点A运动到
A'位置时,点A经过的路线长。
C
A
B
C '
A'
数 学 活 动 室
学 以 致 用
3.如图,⊙O1的半径是⊙O2的直径,C是⊙O1上的一点,O1C交⊙O2于点B,若⊙O1的半径为5cm,AC的长等于⊙O1周长的 ,
求AB的长。
B
A
O1
O2
C
学以致用
【方法点拨】求弧长需要的两个条件:(1)弧所在圆的半径;(2)弧
所对的圆心角。当题中没有直接给出这两个条件时,则需利用圆的相关
知识:弦、弦心距、圆周角、切线等求出圆的半径或弧所对的圆心角.
例 3
如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD
的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF= 米,则这段弯路的长度为( )
A、 米 B、 米
C、 米 D、 米
D
E
C
O
F
A
数 学 活 动 室
经 典 数 学
4.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
数 学 活 动 室
经 典 数 学
5.秋千拉绳长3m,静止时踩板离地面0.5m。某小朋友荡秋千时,秋千在最高处踩板距地面2m(左右对称),如图,则该秋千荡过的圆弧长为( )
A、 B、 C、 D、
O
F
A
B
E
D
B
学以致用
扇形:如图,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形。
O
A
B
n°
l
r
r
探究发现
思考:下图中各扇形面积分别是圆面积的几分之几?
90°
45°
n°
180°
圆心角占
整个周角的
扇形面积
通过刚才的计算,你有何收获呢?
探究发现
如果设圆心角是n的扇形面积为S,圆的半径为r,那么扇形的面积为:
A
B
O
O
180
R
n
l
p
=
探究发现
若设圆心角是n的扇形面积为S,圆的半径为r,则扇形的面积为:
探究发现
(Ⅰ)应用方法:
(Ⅱ)特别注意:
(1)当已知半径r和圆心角求扇形面积时,选用公式
(2)当已知半径r和弧长求扇形的面积时,选用公式
(1)已知S,l,n,r四个量中的任意两个量,可以求出另外两个量;
(2)在扇形公式 中,n,360不带单位。
学以致用
例 4
如图,在□ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分
?
的面积是( )
C
A
B
C
D
A、 B、 C、 D、
【变式】如图,分别以□ABCD四个顶点为圆心,1cm为半径作⊙A、⊙B、
⊙C 、⊙D,求图中阴影部分的面积之和。
A
B
D
C
学以致用
例 5
如图,分别以△ABC三个顶点为圆心,1cm为半径作⊙A、⊙B、⊙C
求图中阴影部分的面积之和。
A
B
B
B
A
C
【拓展】如图,依次以三角形、四边形、……、n边形的各顶点为圆心画
半径为1的圆,且圆与圆之间两两不相交。把三角形与各圆重叠部分面积
之和记为S3,四边形与各圆重叠部分面积之和记为S4, ……,n边形与各圆
重叠部分面积之和记为Sn,求S90的值。
A
B
C
D
数 学 活 动 室
学 以 致 用
1.已知扇形的圆心角为120°,半径为2,求这个扇形的面积;
2.已知扇形面积为 ,圆心角为60°,求这个扇形的半径R;
3.已知半径为2cm的扇形,其弧长为 ,求这个扇形的面积。
4.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇
形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴
纸部分的面积为( )
A、 B、 C、 D、
A
C
O
B
B
学以致用
我是这样想的…
【归纳】解决由弦及其所对的弧组成的图形(即弓形)的方法是:转化
为扇形的面积与三角形的面积之差(和)。
A
例 6
如图,已知扇形AOB的半径为2,圆心角为90°,连结AB,则图中阴影
部分的面积是( )
A、 B、 C、 D、
B
A
O
数 学 活 动 室
经 典 数 学
5.如图,AB为⊙O的切线,切点为B,连结AO,AO与⊙O交于点C,
BD为⊙O的直径,连结CD.若∠A=30°,⊙O的半径为2,则图中
阴影部分的面积为( )
A、 B、
C、 D、
O
B
A
C
D
学以致用
例 7
如图,等腰直角三角形ABC中,AB=AC=8,以AB为直径的半圆O交斜
边BC于点D,求图中阴影部分的面积。
你怎样思考的?
O
C
A
D
B
【技巧】(1)本例中的阴影部分虽然不是规则图形,但它的面积可以转
化为三个规则图形的面积差,因此我们只需分别求出一个扇形面积和
两个三角形面积即可达到目的;(2)求不规则图形面积时,常采用的
方法有:①作差法;②割补法;③拼凑法;④等积变形法;⑤迁移变
换法;⑥化零为整法;⑦平移法。
学以致用
例 8
如图,两个半圆形中,长为24的弦AB与直径CD平行且与小半圆相
【注意】利用平移等图形变换可将不规则图形面积转化为规则图形面积
的和、差进行求解。
切,求图中阴影部分的面积。
B
A
C
D
O
B
A
C
D
O
E
学以致用
例 9
如图,扇形OAB与扇形OCD的圆心角均为90°,连结AC,BD.
【技巧方法】计算不规则图形的面积时,常常通过割补法将不规则图形
的面积转化为及格规则图形面积的和或差的形式。
O
A
B
D
F
C
E
(1)求证:AC=BD;
(2)若图中阴影部分的面积是 ,OA=2cm,求OC的长。
数 学 活 动 室
学 以 致 用
6.如图,已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积S.
D
C
F
E
B
A
数 学 活 动 室
学 以 致 用
7.如图,正六边形内接于⊙O,⊙O的半径为10,求图中阴影部分的面积。
O
8.如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和。
数 学 活 动 室
学 以 致 用
9.如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,O、H分别为AB、AC的中点,将△ABC顺时针旋转120°到△A1BC1的位置,求
整个旋转过程中线段OH所扫过的面积。
A
H
B
O
C
H1
O1
A1
C1
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
