1.1.1 柱、锥、台、球的结构特征(一)
文档属性
| 名称 | 1.1.1 柱、锥、台、球的结构特征(一) |  | |
| 格式 | zip | ||
| 文件大小 | 329.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-07 19:40:34 | ||
图片预览






文档简介
(共26张PPT)
导入新课
我们周围有各种各样的物体,它们都有怎样的结构特征?
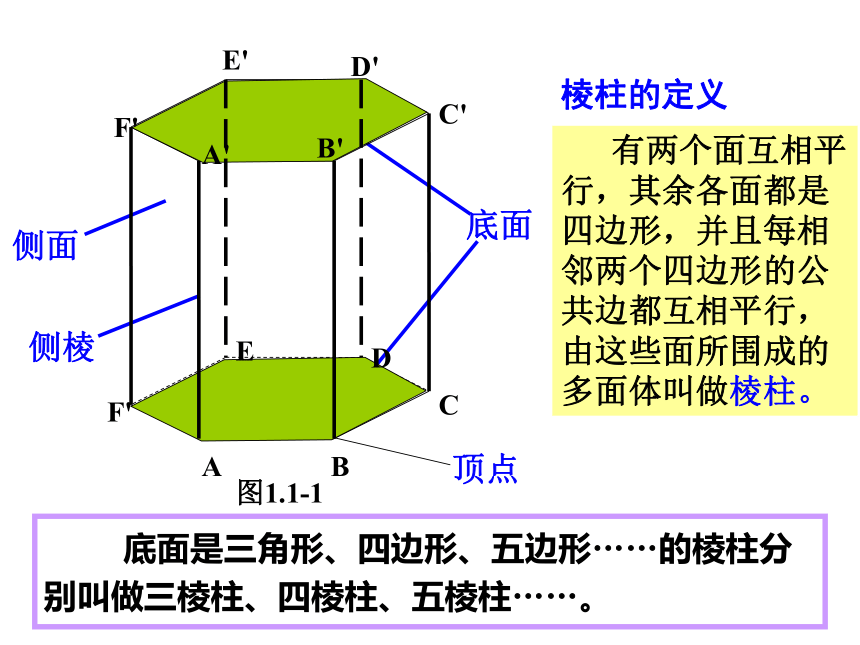
1.棱柱的结构特征
概括上页那些图,它们各自的特点是什么?它们的公共特点是什么?
讨论
1.有两个面互相平行。
2.其余各面都是四边形。
3.每相邻两个四边形的公共边都互相平行。
共同特点:
底面
顶点
侧面
侧棱
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
棱柱的定义
C'
F'
E'
F'
D'
C
D
B'
A'
A
B
E
图1.1-1
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……。
棱柱中,两个互相平行的面叫做棱柱的底面,简称底。
其余各面叫做棱柱的侧面。
相邻侧面的公共边叫做棱柱的侧棱。
侧面与底面的公共顶点叫做棱柱的顶点。
讨论
如何表示一个棱柱呢?
用底面各顶点的字母表示棱柱,如图1.1-1表示为棱柱ABCDEF—A ' B ' C ' D ' E ' F ' 。
D'
C'
B'
A'
A
B
D
C
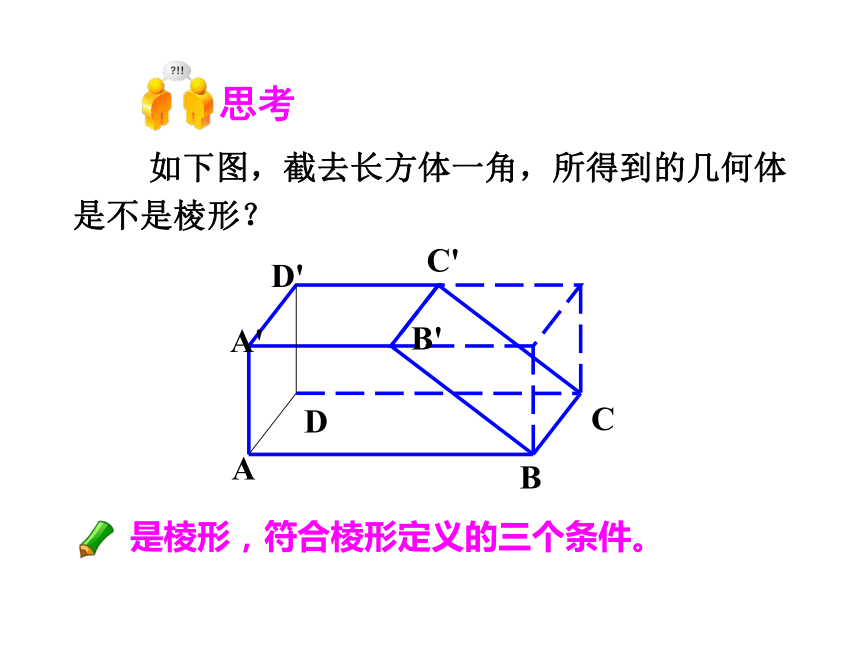
如下图,截去长方体一角,所得到的几何体是不是棱形?
是棱形,符合棱形定义的三个条件。
思考
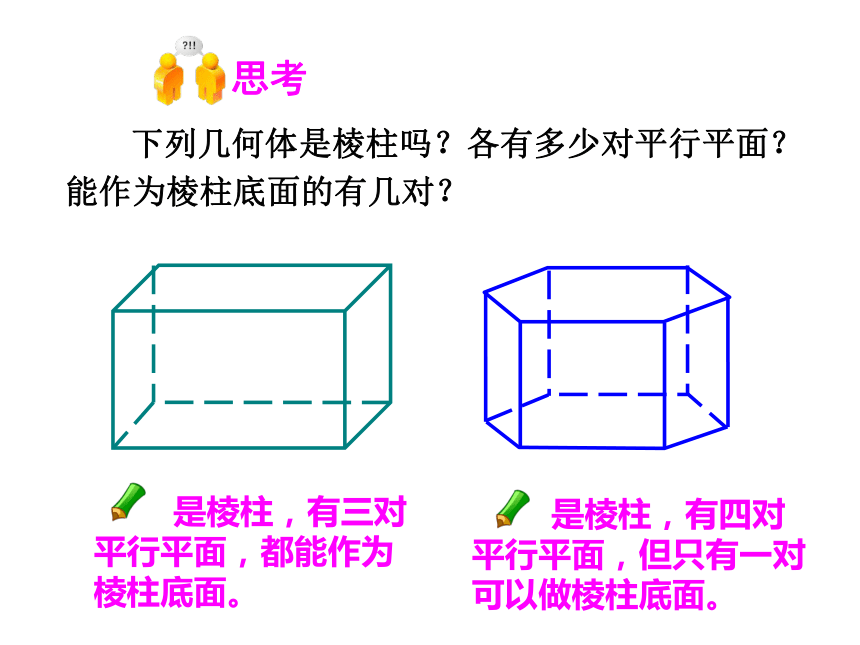
下列几何体是棱柱吗?各有多少对平行平面?能作为棱柱底面的有几对?
思考
是棱柱,有三对平行平面,都能作为棱柱底面。
是棱柱,有四对平行平面,但只有一对可以做棱柱底面。
讨论
有两个面互相平行,其余各面都是平行四边形的几何体是不是棱形?
这样的定义不确切,比如上图符合上述定义,但不是棱形。
反例
按照侧棱分类:
(1)侧棱不垂直于底面的棱柱叫做_______。
(2)侧棱垂直于底面的棱柱叫做______,其中底面是正多边形的直棱柱叫做_______。
斜棱柱
直棱柱
正棱柱
斜棱柱
直棱柱
正棱柱
2. 棱锥的结构特征
概括上面这些图,它们各自的特点是什么?它们的公共特点是什么?
讨论
1.有一个面是多边形。
2.其余各面都是有一个公共顶点的三角形。
共同特点:
侧面
底面
侧棱
顶点
一般的,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱柱。
棱锥的定义
S
D
C
B
A
图1.1-2
底面是三角形、四边形、五边形……的棱锥分别叫做三棱锥、四棱锥、五棱锥…….
这个多边形面叫做棱锥的底面,简称底。
有公共顶点的三角形面叫做棱锥的侧面。
各侧面的公共顶点叫做棱锥的顶点。
相邻侧面的公共边叫做棱锥的侧棱。
棱锥与棱柱表示方法类似,棱锥也用表示顶点和底面各顶点的字母表示,如图1.1-2表示为棱锥S-ABCD。
如何表示一个棱锥呢?
棱柱与棱锥的差别是什么?怎样由一个棱柱得到棱锥?
思考
三棱锥是最简单的空间几何体之一,它有四个面,每个面都是三角形,每个三角形的顶点都可以作为三棱锥的顶点,每一个面都可以作为底面。
长方体中的三棱锥
S
A
B
C
S-ABC
注意
3. 棱台的结构特征
上面这些多面体,是用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
棱台的定义
上底面
下底面
原棱锥的底面叫做棱台的下底面,截面叫做棱台的上底面。
探
究
棱台也有侧面、侧棱、顶点。
顶点
侧棱
侧面
O
A'
B'
C'
D'
A
B
C
D
图1.1-3
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……,如图1.1-2表示为棱台ABCDEF-A ' B ' C ' D ' E ' F ' 。
棱台可由棱锥转化而来,棱台问题常可转化成棱锥问题求解。
棱柱、棱锥、棱台都是多面体。
总结
棱柱、棱锥、棱台都是多面体。
总结
1. 下列关于多面体的说法中:
(1)底面是矩形的直棱柱是长方体;
(2)底面是正方形的棱锥是正四棱锥;
(3)两底面都是正方形的棱台是正棱台;
(4)正四棱柱就是正方体。
其中正确的是_________
(1)
课堂练习
2. 下列图中,不是正方体的表面展开图的是( )
A
B
C
C
D
3. 正方体的六个面分别涂有红,蓝,黄,绿,黑,白六种颜色,根据下图所示,绿色面的相对面是_______色。
绿
红
黄
黑
黄
蓝
蓝
4. 有一个正棱锥所有的棱长都相等,则这个正棱锥不可能是( )
A. 正三棱锥 B. 正四棱锥
C. 正五棱锥 D. 正六棱锥
D
导入新课
我们周围有各种各样的物体,它们都有怎样的结构特征?
1.棱柱的结构特征
概括上页那些图,它们各自的特点是什么?它们的公共特点是什么?
讨论
1.有两个面互相平行。
2.其余各面都是四边形。
3.每相邻两个四边形的公共边都互相平行。
共同特点:
底面
顶点
侧面
侧棱
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
棱柱的定义
C'
F'
E'
F'
D'
C
D
B'
A'
A
B
E
图1.1-1
底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……。
棱柱中,两个互相平行的面叫做棱柱的底面,简称底。
其余各面叫做棱柱的侧面。
相邻侧面的公共边叫做棱柱的侧棱。
侧面与底面的公共顶点叫做棱柱的顶点。
讨论
如何表示一个棱柱呢?
用底面各顶点的字母表示棱柱,如图1.1-1表示为棱柱ABCDEF—A ' B ' C ' D ' E ' F ' 。
D'
C'
B'
A'
A
B
D
C
如下图,截去长方体一角,所得到的几何体是不是棱形?
是棱形,符合棱形定义的三个条件。
思考
下列几何体是棱柱吗?各有多少对平行平面?能作为棱柱底面的有几对?
思考
是棱柱,有三对平行平面,都能作为棱柱底面。
是棱柱,有四对平行平面,但只有一对可以做棱柱底面。
讨论
有两个面互相平行,其余各面都是平行四边形的几何体是不是棱形?
这样的定义不确切,比如上图符合上述定义,但不是棱形。
反例
按照侧棱分类:
(1)侧棱不垂直于底面的棱柱叫做_______。
(2)侧棱垂直于底面的棱柱叫做______,其中底面是正多边形的直棱柱叫做_______。
斜棱柱
直棱柱
正棱柱
斜棱柱
直棱柱
正棱柱
2. 棱锥的结构特征
概括上面这些图,它们各自的特点是什么?它们的公共特点是什么?
讨论
1.有一个面是多边形。
2.其余各面都是有一个公共顶点的三角形。
共同特点:
侧面
底面
侧棱
顶点
一般的,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱柱。
棱锥的定义
S
D
C
B
A
图1.1-2
底面是三角形、四边形、五边形……的棱锥分别叫做三棱锥、四棱锥、五棱锥…….
这个多边形面叫做棱锥的底面,简称底。
有公共顶点的三角形面叫做棱锥的侧面。
各侧面的公共顶点叫做棱锥的顶点。
相邻侧面的公共边叫做棱锥的侧棱。
棱锥与棱柱表示方法类似,棱锥也用表示顶点和底面各顶点的字母表示,如图1.1-2表示为棱锥S-ABCD。
如何表示一个棱锥呢?
棱柱与棱锥的差别是什么?怎样由一个棱柱得到棱锥?
思考
三棱锥是最简单的空间几何体之一,它有四个面,每个面都是三角形,每个三角形的顶点都可以作为三棱锥的顶点,每一个面都可以作为底面。
长方体中的三棱锥
S
A
B
C
S-ABC
注意
3. 棱台的结构特征
上面这些多面体,是用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
棱台的定义
上底面
下底面
原棱锥的底面叫做棱台的下底面,截面叫做棱台的上底面。
探
究
棱台也有侧面、侧棱、顶点。
顶点
侧棱
侧面
O
A'
B'
C'
D'
A
B
C
D
图1.1-3
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……,如图1.1-2表示为棱台ABCDEF-A ' B ' C ' D ' E ' F ' 。
棱台可由棱锥转化而来,棱台问题常可转化成棱锥问题求解。
棱柱、棱锥、棱台都是多面体。
总结
棱柱、棱锥、棱台都是多面体。
总结
1. 下列关于多面体的说法中:
(1)底面是矩形的直棱柱是长方体;
(2)底面是正方形的棱锥是正四棱锥;
(3)两底面都是正方形的棱台是正棱台;
(4)正四棱柱就是正方体。
其中正确的是_________
(1)
课堂练习
2. 下列图中,不是正方体的表面展开图的是( )
A
B
C
C
D
3. 正方体的六个面分别涂有红,蓝,黄,绿,黑,白六种颜色,根据下图所示,绿色面的相对面是_______色。
绿
红
黄
黑
黄
蓝
蓝
4. 有一个正棱锥所有的棱长都相等,则这个正棱锥不可能是( )
A. 正三棱锥 B. 正四棱锥
C. 正五棱锥 D. 正六棱锥
D
