6.1 圆周运动 同步练习 —2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案)
文档属性
| 名称 | 6.1 圆周运动 同步练习 —2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 828.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-11 07:28:45 | ||
图片预览




文档简介
第六章 圆周运动
1.圆周运动
1.对于做匀速圆周运动的物体,下列说法中错误的是( )
A.相等的时间内通过的路程相等
B.相等的时间内通过的弧长相等
C.相等的时间内通过的位移相等
D.相等的时间内转过的角度相等
2.甲、乙两物体分别做匀速圆周运动,如果它们转动的半径之比为1∶5,线速度之比为3∶2,则下列说法正确的是( )
A.甲、乙两物体的角速度之比是2∶15
B.甲、乙两物体的角速度之比是10∶3
C.甲、乙两物体的周期之比是2∶15
D.甲、乙两物体的周期之比是10∶3
3.把某一机械手表的分针与时针上的点看成是匀速圆周运动,且分针长度是时针长度的1.5倍,则( )
A.分针与时针的周期之比为1∶60
B.分针与时针的角速度之比为12∶1
C.分针与时针末端的线速度之比为8∶1
D.分针与时针的频率之比为1∶12
4.甲沿着半径为R的圆周跑道匀速跑步,乙沿着半径为2R的圆周跑道匀速跑步。在相同的时间内,甲、乙各自跑了一圈,他们的角速度分别为ω1、ω2,线速度大小分别为v1、v2,频率分别为f1、f2,则( )
A.ω1>ω2,f1>f2 B.ω1=ω2,f1C.ω1=ω2,v1<v2 D.ω1<ω2,v1>v2
5.嘉兴某高中开设了糕点制作的选修课,小明同学在体验糕点制作的“裱花”环节时,如图所示,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕边缘上每隔4 s“点”一次奶油,蛋糕随圆盘转一周后均匀“点”上了15次奶油,则下列说法正确的是( )
A.圆盘转动的转速约为2π r/min
B.圆盘转动的角速度大小约为 rad/s
C.蛋糕边缘的奶油的线速度大小约为 m/s
D.圆盘转动的频率约为 Hz
6. 如图所示,A、B是两个摩擦传动的靠背轮。A是主动轮,B是从动轮,它们的半径RA=2RB,a和b两点在各轮的边缘,c和d在各轮半径的中点,下列判断正确的是( )
A.va=2vb B.ωa=2ωc
C.ωd=ωc D.vb=2vc
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点,则偏心轮转动过程中,a、b两点( )
A.角速度大小相同
B.线速度大小相同
C.周期大小不同
D.转速大小不同
8.如图所示是中国古代玩具饮水鸟的示意图,它的神奇之处是,在鸟的面前放上一杯水,鸟就会俯下身去,把嘴浸到水里,“喝”了一口水后,鸟将绕着O点不停摆动,一会儿它又会俯下身去,再“喝”一口水。P、Q是饮水鸟上两点,且rPO>rQO,则在摆动过程中( )
A.P点的线速度小于Q点的线速度
B.P、Q两点的角速度大小相等
C.相同时间内P、Q两点通过的弧长相等
D.P、Q两点的线速度大小相等、方向相反
9.变速自行车靠变换齿轮组合来改变行驶速度,如图是某一变速车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
A.该车可变换两种不同挡位
B.该车可变换八种不同挡位
C.当A轮与D轮组合时,两轮的角速度之比ωA∶ωD=1∶4
D.当A轮与D轮组合时,两轮的角速度之比ωA∶ωD=4∶1
10 .如图所示的齿轮传动装置中,主动轮和从动轮的齿大小相同,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω逆时针转动时,从动轮的转动情况是( )
A.顺时针转动,周期为
B.逆时针转动,周期为
C.顺时针转动,周期为
D.逆时针转动,周期为
11 . 关于做匀速圆周运动的物体的线速度、角速度、周期的关系,下列说法中正确的是( )
A.线速度大的角速度一定大
B.线速度大的周期一定小
C.角速度大的运动半径一定小
D.角速度大的周期一定小
12.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min,子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示。则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
13.关于匀速圆周运动,下列说法错误的是( )
A.匀速圆周运动是变速运动
B.匀速圆周运动的速率不变
C.任意相等时间内通过的位移相等
D.任意相等时间内通过的路程相等
14.对于做匀速圆周运动的物体,下列说法正确的是( )
A.根据T=,线速度越大,则周期越小
B.根据T=,角速度越大,则周期越小
C.角速度越大,速度的大小变化越快
D.线速度越大,速度的方向变化越快
15.某品牌的机械鼠标内部构造如图所示,机械鼠标中的定位球的直径是2 cm,某次操作中将鼠标沿直线匀速移动12 cm需要1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
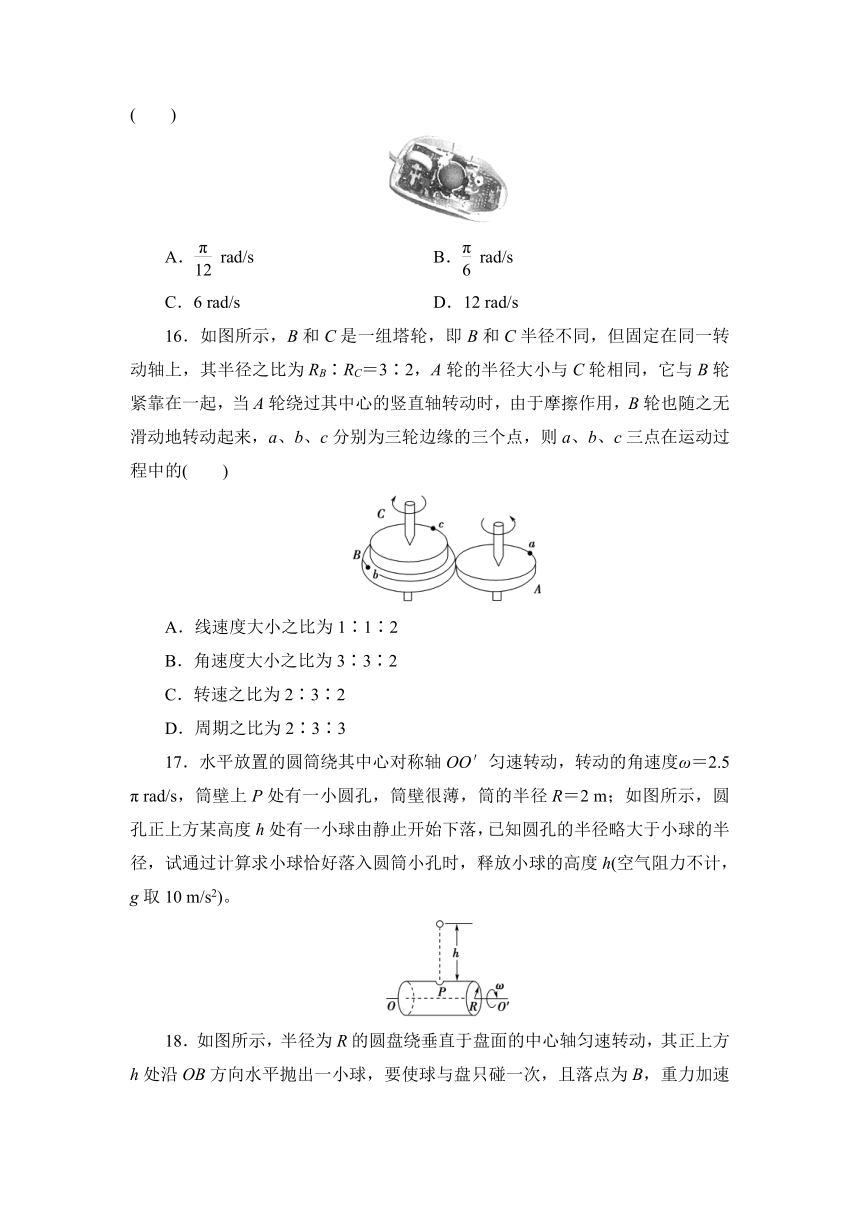
16.如图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB∶RC=3∶2,A轮的半径大小与C轮相同,它与B轮紧靠在一起,当A轮绕过其中心的竖直轴转动时,由于摩擦作用,B轮也随之无滑动地转动起来,a、b、c分别为三轮边缘的三个点,则a、b、c三点在运动过程中的( )
A.线速度大小之比为1∶1∶2
B.角速度大小之比为3∶3∶2
C.转速之比为2∶3∶2
D.周期之比为2∶3∶3
17.水平放置的圆筒绕其中心对称轴OO′匀速转动,转动的角速度ω=2.5 π rad/s,筒壁上P处有一小圆孔,筒壁很薄,筒的半径R=2 m;如图所示,圆孔正上方某高度h处有一小球由静止开始下落,已知圆孔的半径略大于小球的半径,试通过计算求小球恰好落入圆筒小孔时,释放小球的高度h(空气阻力不计,g取10 m/s2)。
18.如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h处沿OB方向水平抛出一小球,要使球与盘只碰一次,且落点为B,重力加速度为g,求小球的初速度和圆盘转动的角速度ω。
19. 做匀速圆周运动的物体,10 s内沿半径为20 m的圆周运动100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
20.如图所示,B物体放在光滑的水平地面上,在水平力F的作用下由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动。求满足使A、B速度相同的力F的取值。
参考解析
1 C [做匀速圆周运动的物体,相等的时间内通过的路程相等、通过的弧长相等、转过的角度相等,A、B、D正确;位移是矢量,相等的时间内通过的位移大小相等、方向不一定相同,故位移不一定相等,C错误。]
2 C [由v=ωr得==·=×=,A、B错误;由ω=得==,C正确,D错误。]
3 B [分针的周期为T分=1 h,时针的周期为T时=12 h,则分针与时针的周期之比为T分∶T时=1∶12,由ω=可知,分针与时针的角速度之比为ω分∶ω时=12∶1,由f=可知,分针与时针的频率之比为f分∶f时=12∶1,A、D错误,B正确;由v=ωr得,分针与时针末端的线速度之比为v分∶v时=ω分r分∶ω时r时=18∶1,C错误。]
4 C [由题意知,甲、乙两人跑步的周期T相同,由f=知,甲、乙两人跑步的频率相同,即f1=f2;由ω=知,甲、乙两人的角速度相同,即ω1=ω2;由v=知,v1<v2。C正确。]
5 B [由题意可知,圆盘转一周所需的时间为15×4 s=60 s,因此周期为60 s,转速为1 r/min,A错误;由角速度与周期的关系可得ω==rad/s= rad/s,B正确;蛋糕边缘的奶油的线速度大小为v=ωr= m/s,C错误;根据周期和频率的关系可得圆盘转动的频率为f==Hz,D错误。]
6 D [由于A、B两轮之间通过摩擦传动,故A、B两轮的边缘的线速度大小相同,所以va=vb,故A错误;a、c两点同轴转动,角速度相等,所以ωa=ωc,故B错误;根据v=ωR可得,ωaRA=ωbRB,则ωa∶ωb=RB∶RA=1∶2,即ωb=2ωa,a、c两点角速度相等,b、d两点角速度相等,所以ωd=2ωc,故C错误;由于ωa=ωc,Ra=2Rc,故va∶vc=2∶1,即va=2vc,又va=vb,所以vb=2vc,故D正确。]
7 A [同轴转动,角速度大小相等,周期、转速都相等,选项A正确,C、D错误;角速度大小相等,但转动半径不同,根据v=ωr可知,线速度大小不同,选项B错误。]
8 B [鸟将绕着O点不停摆动,P、Q是饮水鸟上两点,属于同轴转动。P点离O点更远,绕O点转动的半径大。根据同轴转动角速度相等知P、Q两点的角速度大小相等,故B正确;P、Q两点的角速度大小相同,P点绕O点转动的半径大,根据v=ωr知,P点的线速度较大,故A、D错误;P、Q两点的线速度大小不同,故相同时间内通过的弧长不相等,故C错误。]
9 C [A轮通过链条分别与C、D连接,自行车可有两种速度,B轮分别与C、D连接,又可有两种速度,所以该车可变换4种挡位,故A、B错误;当A与D组合时,两轮边缘线速度大小相等,A轮转一圈,D转4圈,即=,故C正确,D错误。]
10 A [齿轮不打滑,说明接触点线速度相等,主动轮逆时针转动,故从动轮顺时针转动。因为齿的大小相等,主动轮的齿数z1=24,从动轮的齿数z2=8,故主动轮与从动轮的角速度之比==,解得从动轮的角速度ω2=3ω1=3ω。由ω=得从动轮的周期T==,故A正确。]
11 D [由v=ωr知,r一定时,v与ω成正比;v一定时,ω与r成反比,故AC错误。由v=知,r一定时,v越大,T越小,故B错误。由ω=可知,ω越大,T越小,故D正确。]
12C [子弹从A盘到B盘,B盘转过的角度θ=2πn+(n=0,1,2,…),B盘转动的角速度ω==2πf=2πn=2π× rad/s=120π rad/s,子弹在A、B盘间运动的时间等于B盘转动的时间,即=,所以v== m/s(n=0,1,2,…),n=0时,v=1 440 m/s;n=1时,v≈110.77 m/s;n=2时,v=57.6 m/s,C正确。]
13C [由匀速圆周运动的定义知,做匀速圆周运动的物体速度的大小不变,也就是速率不变,但速度方向时刻改变,故A、B两项正确;做匀速圆周运动的物体在任意相等时间内通过的弧长即路程相等,但通过的位移不一定相等,故D项正确,C项错误。本题错误的选C。]
14 B [根据T=,当轨道半径一定时,才有线速度越大,周期越小,选项A错误;角速度越大,周期越小,选项B正确;单位时间内质点与圆心的连线(圆半径)转过的角度越大,速度的方向变化越快,选项C、D错误。]
15 D [根据线速度定义式有v=,那么定位球的线速度为v==12 cm/s,而线速度与角速度的关系为v=ωr,则定位球的角速度为ω===12 rad/s,故A、B、C错误,D正确。]
16 D [A轮、B轮靠摩擦传动,边缘点的线速度大小相等,故va∶vb=1∶1,根据公式v=rω,有ωa∶ωb=3∶2,根据ω=2πn,有na∶nb=3∶2,根据T=,有Ta∶Tb=2∶3;B轮、C轮是同轴传动,角速度相等,故ωb∶ωc=1∶1,根据v=rω,有vb∶vc=3∶2,根据ω=2πn,有nb∶nc=1∶1,根据T=,有Tb∶Tc=1∶1,联立可得va∶vb∶vc=3∶3∶2,ωa∶ωb∶ωc=3∶2∶2,na∶nb∶nc=3∶2∶2,Ta∶Tb∶Tc=2∶3∶3。故D正确,A、B、C错误。]
17[答案] h=k2(k=1,2,3…)
[解析] 设小球做自由落体运动下落h高度历时为t,
则:h=gt2,
要使小球恰好落入小孔,对于圆筒的运动需满足:
2kπ=ωt,(k=1,2,3…)
联立以上两式并代入数据,
解得释放小球的高度h为:
h=k2(k=1,2,3…)。
18[答案] R 2nπ(n=1,2,3…)
[解析] 小球做平抛运动,在竖直方向上h=gt2,则运动时间t=。又因为水平位移为R
所以小球的初速度v==R·
在时间t内圆盘转过的角度θ=n·2π(n=1,2,3…),其中n为圆盘转动的圈数,
又因为θ=ωt,则圆盘角速度ω==2nπ(n=1,2,3…)。
19[答案] (1)10 m/s (2)0.5 rad/s (3)4π s
[解析] (1)依据线速度的定义式可得v== m/s=10 m/s。
(2)依据v=ωr可得ω== rad/s=0.5 rad/s。
(3)T== s=4π s。
20[答案] F=(n=0,1,2…)
[解析] 速度相同即大小、方向相同,B为水平向右,A一定要在最低点才能保证速度水平向右。由题意可知:当A从M点运动到最低点时
t=nT+T(n=0,1,2…),线速度v=ωr
对于B(初速度为0):
v=at==
解得:F=(n=0,1,2…)。
1.圆周运动
1.对于做匀速圆周运动的物体,下列说法中错误的是( )
A.相等的时间内通过的路程相等
B.相等的时间内通过的弧长相等
C.相等的时间内通过的位移相等
D.相等的时间内转过的角度相等
2.甲、乙两物体分别做匀速圆周运动,如果它们转动的半径之比为1∶5,线速度之比为3∶2,则下列说法正确的是( )
A.甲、乙两物体的角速度之比是2∶15
B.甲、乙两物体的角速度之比是10∶3
C.甲、乙两物体的周期之比是2∶15
D.甲、乙两物体的周期之比是10∶3
3.把某一机械手表的分针与时针上的点看成是匀速圆周运动,且分针长度是时针长度的1.5倍,则( )
A.分针与时针的周期之比为1∶60
B.分针与时针的角速度之比为12∶1
C.分针与时针末端的线速度之比为8∶1
D.分针与时针的频率之比为1∶12
4.甲沿着半径为R的圆周跑道匀速跑步,乙沿着半径为2R的圆周跑道匀速跑步。在相同的时间内,甲、乙各自跑了一圈,他们的角速度分别为ω1、ω2,线速度大小分别为v1、v2,频率分别为f1、f2,则( )
A.ω1>ω2,f1>f2 B.ω1=ω2,f1
5.嘉兴某高中开设了糕点制作的选修课,小明同学在体验糕点制作的“裱花”环节时,如图所示,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕边缘上每隔4 s“点”一次奶油,蛋糕随圆盘转一周后均匀“点”上了15次奶油,则下列说法正确的是( )
A.圆盘转动的转速约为2π r/min
B.圆盘转动的角速度大小约为 rad/s
C.蛋糕边缘的奶油的线速度大小约为 m/s
D.圆盘转动的频率约为 Hz
6. 如图所示,A、B是两个摩擦传动的靠背轮。A是主动轮,B是从动轮,它们的半径RA=2RB,a和b两点在各轮的边缘,c和d在各轮半径的中点,下列判断正确的是( )
A.va=2vb B.ωa=2ωc
C.ωd=ωc D.vb=2vc
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点,则偏心轮转动过程中,a、b两点( )
A.角速度大小相同
B.线速度大小相同
C.周期大小不同
D.转速大小不同
8.如图所示是中国古代玩具饮水鸟的示意图,它的神奇之处是,在鸟的面前放上一杯水,鸟就会俯下身去,把嘴浸到水里,“喝”了一口水后,鸟将绕着O点不停摆动,一会儿它又会俯下身去,再“喝”一口水。P、Q是饮水鸟上两点,且rPO>rQO,则在摆动过程中( )
A.P点的线速度小于Q点的线速度
B.P、Q两点的角速度大小相等
C.相同时间内P、Q两点通过的弧长相等
D.P、Q两点的线速度大小相等、方向相反
9.变速自行车靠变换齿轮组合来改变行驶速度,如图是某一变速车齿轮转动结构示意图,图中A轮有48齿,B轮有42齿,C轮有18齿,D轮有12齿,则( )
A.该车可变换两种不同挡位
B.该车可变换八种不同挡位
C.当A轮与D轮组合时,两轮的角速度之比ωA∶ωD=1∶4
D.当A轮与D轮组合时,两轮的角速度之比ωA∶ωD=4∶1
10 .如图所示的齿轮传动装置中,主动轮和从动轮的齿大小相同,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω逆时针转动时,从动轮的转动情况是( )
A.顺时针转动,周期为
B.逆时针转动,周期为
C.顺时针转动,周期为
D.逆时针转动,周期为
11 . 关于做匀速圆周运动的物体的线速度、角速度、周期的关系,下列说法中正确的是( )
A.线速度大的角速度一定大
B.线速度大的周期一定小
C.角速度大的运动半径一定小
D.角速度大的周期一定小
12.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min,子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示。则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
13.关于匀速圆周运动,下列说法错误的是( )
A.匀速圆周运动是变速运动
B.匀速圆周运动的速率不变
C.任意相等时间内通过的位移相等
D.任意相等时间内通过的路程相等
14.对于做匀速圆周运动的物体,下列说法正确的是( )
A.根据T=,线速度越大,则周期越小
B.根据T=,角速度越大,则周期越小
C.角速度越大,速度的大小变化越快
D.线速度越大,速度的方向变化越快
15.某品牌的机械鼠标内部构造如图所示,机械鼠标中的定位球的直径是2 cm,某次操作中将鼠标沿直线匀速移动12 cm需要1 s,则定位球的角速度为( )
A. rad/s B. rad/s
C.6 rad/s D.12 rad/s
16.如图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB∶RC=3∶2,A轮的半径大小与C轮相同,它与B轮紧靠在一起,当A轮绕过其中心的竖直轴转动时,由于摩擦作用,B轮也随之无滑动地转动起来,a、b、c分别为三轮边缘的三个点,则a、b、c三点在运动过程中的( )
A.线速度大小之比为1∶1∶2
B.角速度大小之比为3∶3∶2
C.转速之比为2∶3∶2
D.周期之比为2∶3∶3
17.水平放置的圆筒绕其中心对称轴OO′匀速转动,转动的角速度ω=2.5 π rad/s,筒壁上P处有一小圆孔,筒壁很薄,筒的半径R=2 m;如图所示,圆孔正上方某高度h处有一小球由静止开始下落,已知圆孔的半径略大于小球的半径,试通过计算求小球恰好落入圆筒小孔时,释放小球的高度h(空气阻力不计,g取10 m/s2)。
18.如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h处沿OB方向水平抛出一小球,要使球与盘只碰一次,且落点为B,重力加速度为g,求小球的初速度和圆盘转动的角速度ω。
19. 做匀速圆周运动的物体,10 s内沿半径为20 m的圆周运动100 m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小。
20.如图所示,B物体放在光滑的水平地面上,在水平力F的作用下由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动。求满足使A、B速度相同的力F的取值。
参考解析
1 C [做匀速圆周运动的物体,相等的时间内通过的路程相等、通过的弧长相等、转过的角度相等,A、B、D正确;位移是矢量,相等的时间内通过的位移大小相等、方向不一定相同,故位移不一定相等,C错误。]
2 C [由v=ωr得==·=×=,A、B错误;由ω=得==,C正确,D错误。]
3 B [分针的周期为T分=1 h,时针的周期为T时=12 h,则分针与时针的周期之比为T分∶T时=1∶12,由ω=可知,分针与时针的角速度之比为ω分∶ω时=12∶1,由f=可知,分针与时针的频率之比为f分∶f时=12∶1,A、D错误,B正确;由v=ωr得,分针与时针末端的线速度之比为v分∶v时=ω分r分∶ω时r时=18∶1,C错误。]
4 C [由题意知,甲、乙两人跑步的周期T相同,由f=知,甲、乙两人跑步的频率相同,即f1=f2;由ω=知,甲、乙两人的角速度相同,即ω1=ω2;由v=知,v1<v2。C正确。]
5 B [由题意可知,圆盘转一周所需的时间为15×4 s=60 s,因此周期为60 s,转速为1 r/min,A错误;由角速度与周期的关系可得ω==rad/s= rad/s,B正确;蛋糕边缘的奶油的线速度大小为v=ωr= m/s,C错误;根据周期和频率的关系可得圆盘转动的频率为f==Hz,D错误。]
6 D [由于A、B两轮之间通过摩擦传动,故A、B两轮的边缘的线速度大小相同,所以va=vb,故A错误;a、c两点同轴转动,角速度相等,所以ωa=ωc,故B错误;根据v=ωR可得,ωaRA=ωbRB,则ωa∶ωb=RB∶RA=1∶2,即ωb=2ωa,a、c两点角速度相等,b、d两点角速度相等,所以ωd=2ωc,故C错误;由于ωa=ωc,Ra=2Rc,故va∶vc=2∶1,即va=2vc,又va=vb,所以vb=2vc,故D正确。]
7 A [同轴转动,角速度大小相等,周期、转速都相等,选项A正确,C、D错误;角速度大小相等,但转动半径不同,根据v=ωr可知,线速度大小不同,选项B错误。]
8 B [鸟将绕着O点不停摆动,P、Q是饮水鸟上两点,属于同轴转动。P点离O点更远,绕O点转动的半径大。根据同轴转动角速度相等知P、Q两点的角速度大小相等,故B正确;P、Q两点的角速度大小相同,P点绕O点转动的半径大,根据v=ωr知,P点的线速度较大,故A、D错误;P、Q两点的线速度大小不同,故相同时间内通过的弧长不相等,故C错误。]
9 C [A轮通过链条分别与C、D连接,自行车可有两种速度,B轮分别与C、D连接,又可有两种速度,所以该车可变换4种挡位,故A、B错误;当A与D组合时,两轮边缘线速度大小相等,A轮转一圈,D转4圈,即=,故C正确,D错误。]
10 A [齿轮不打滑,说明接触点线速度相等,主动轮逆时针转动,故从动轮顺时针转动。因为齿的大小相等,主动轮的齿数z1=24,从动轮的齿数z2=8,故主动轮与从动轮的角速度之比==,解得从动轮的角速度ω2=3ω1=3ω。由ω=得从动轮的周期T==,故A正确。]
11 D [由v=ωr知,r一定时,v与ω成正比;v一定时,ω与r成反比,故AC错误。由v=知,r一定时,v越大,T越小,故B错误。由ω=可知,ω越大,T越小,故D正确。]
12C [子弹从A盘到B盘,B盘转过的角度θ=2πn+(n=0,1,2,…),B盘转动的角速度ω==2πf=2πn=2π× rad/s=120π rad/s,子弹在A、B盘间运动的时间等于B盘转动的时间,即=,所以v== m/s(n=0,1,2,…),n=0时,v=1 440 m/s;n=1时,v≈110.77 m/s;n=2时,v=57.6 m/s,C正确。]
13C [由匀速圆周运动的定义知,做匀速圆周运动的物体速度的大小不变,也就是速率不变,但速度方向时刻改变,故A、B两项正确;做匀速圆周运动的物体在任意相等时间内通过的弧长即路程相等,但通过的位移不一定相等,故D项正确,C项错误。本题错误的选C。]
14 B [根据T=,当轨道半径一定时,才有线速度越大,周期越小,选项A错误;角速度越大,周期越小,选项B正确;单位时间内质点与圆心的连线(圆半径)转过的角度越大,速度的方向变化越快,选项C、D错误。]
15 D [根据线速度定义式有v=,那么定位球的线速度为v==12 cm/s,而线速度与角速度的关系为v=ωr,则定位球的角速度为ω===12 rad/s,故A、B、C错误,D正确。]
16 D [A轮、B轮靠摩擦传动,边缘点的线速度大小相等,故va∶vb=1∶1,根据公式v=rω,有ωa∶ωb=3∶2,根据ω=2πn,有na∶nb=3∶2,根据T=,有Ta∶Tb=2∶3;B轮、C轮是同轴传动,角速度相等,故ωb∶ωc=1∶1,根据v=rω,有vb∶vc=3∶2,根据ω=2πn,有nb∶nc=1∶1,根据T=,有Tb∶Tc=1∶1,联立可得va∶vb∶vc=3∶3∶2,ωa∶ωb∶ωc=3∶2∶2,na∶nb∶nc=3∶2∶2,Ta∶Tb∶Tc=2∶3∶3。故D正确,A、B、C错误。]
17[答案] h=k2(k=1,2,3…)
[解析] 设小球做自由落体运动下落h高度历时为t,
则:h=gt2,
要使小球恰好落入小孔,对于圆筒的运动需满足:
2kπ=ωt,(k=1,2,3…)
联立以上两式并代入数据,
解得释放小球的高度h为:
h=k2(k=1,2,3…)。
18[答案] R 2nπ(n=1,2,3…)
[解析] 小球做平抛运动,在竖直方向上h=gt2,则运动时间t=。又因为水平位移为R
所以小球的初速度v==R·
在时间t内圆盘转过的角度θ=n·2π(n=1,2,3…),其中n为圆盘转动的圈数,
又因为θ=ωt,则圆盘角速度ω==2nπ(n=1,2,3…)。
19[答案] (1)10 m/s (2)0.5 rad/s (3)4π s
[解析] (1)依据线速度的定义式可得v== m/s=10 m/s。
(2)依据v=ωr可得ω== rad/s=0.5 rad/s。
(3)T== s=4π s。
20[答案] F=(n=0,1,2…)
[解析] 速度相同即大小、方向相同,B为水平向右,A一定要在最低点才能保证速度水平向右。由题意可知:当A从M点运动到最低点时
t=nT+T(n=0,1,2…),线速度v=ωr
对于B(初速度为0):
v=at==
解得:F=(n=0,1,2…)。
