8.1 功与功率 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案)
文档属性
| 名称 | 8.1 功与功率 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-11 08:04:23 | ||
图片预览




文档简介
第八章 机械能守恒定律
1.功与功率
1.如图所示,稳站在商店自动扶梯水平踏板上的人,随扶梯斜向上做加速运动,则在此过程中( )
A.人只受到重力和踏板的支持力作用
B.人受到的重力和踏板的支持力大小相等方向相反
C.支持力对人做正功
D.支持力对人做功为零
2.如图甲、乙所示,质量分别为M和m的两物块,M>m,分别在同样大小的恒力F作用下,沿水平面由静止开始做直线运动,F与水平面的夹角相同。经过相同的位移,设F对M做的功为W1,对m做的功为W2,则( )
甲 乙
A.无论水平面光滑与否,都有W1=W2
B.若水平面光滑,则W1>W2
C.若水平面粗糙,则W1>W2
D.若水平面粗糙,则W1<W2
3.质量为m的木块静止在光滑的水平地面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在0~t1时间内力F做的功是( )
A. B. C. D.
4.关于功率的概念,下列说法中正确的是( )
A.功率是表示力做功快慢的物理量
B.功率是表示力做功多少的物理量
C.由P=可知,功率与时间成反比
D.只要F不为零,v也不为零,这个力的功率P就一定不为零
5.为了响应公共交通出行的环保倡议,小明骑公共自行车上下班。假设在平直公路上自行车所受阻力约为车和人总重的,则小明以正常速度骑行时的功率最接近于( )
A.1 W B.100 W
C.10 kW D.100 kW
6.如图所示,质量为2 kg的物体以10 m/s的初速度水平抛出,经过2 s 落地。g取10 m/s2。关于重力做功的功率,下列说法正确的是( )
A.下落过程中重力的平均功率是400 W
B.下落过程中重力的平均功率是100 W
C.落地前的瞬间重力的瞬时功率是400 W
D.落地前的瞬间重力的瞬时功率是200 W
7.质量为m的汽车,其发动机额定功率为P。当它开上一个倾角为θ的斜坡时,受到的摩擦阻力为车重力的k倍,则车的最大速度为( )
A. B.
C. D.
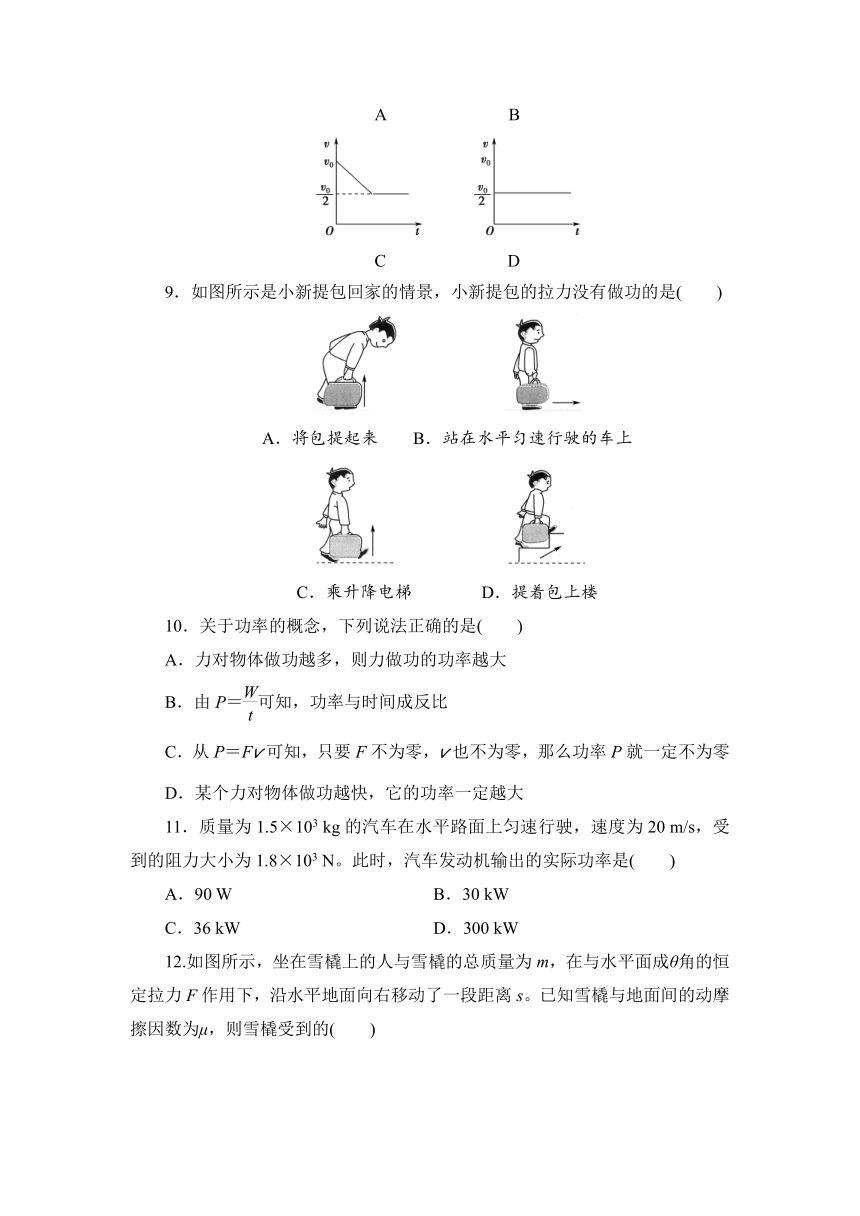
8.汽车在平直公路上以速度v0匀速行驶,发动机功率为P,快进入闹市区时,司机减小了油门,使汽车的功率立即减小为,并保持此功率继续在平直公路上行驶。设汽车行驶时所受的阻力恒定,则能正确反映从减小油门开始汽车的速度随时间变化的图像是( )
A B
C D
9.如图所示是小新提包回家的情景,小新提包的拉力没有做功的是( )
A.将包提起来 B.站在水平匀速行驶的车上
C.乘升降电梯 D.提着包上楼
10.关于功率的概念,下列说法正确的是( )
A.力对物体做功越多,则力做功的功率越大
B.由P=可知,功率与时间成反比
C.从P=Fv可知,只要F不为零,v也不为零,那么功率P就一定不为零
D.某个力对物体做功越快,它的功率一定越大
11.质量为1.5×103 kg的汽车在水平路面上匀速行驶,速度为20 m/s,受到的阻力大小为1.8×103 N。此时,汽车发动机输出的实际功率是( )
A.90 W B.30 kW
C.36 kW D.300 kW
12.如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离s。已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )
A.支持力做功为mgs
B.重力做功为mgs
C.拉力做功为Fscos θ
D.滑动摩擦力做功为-μmgs
13.如图所示,水平路面上有一辆质量为M的汽车,车厢中有一个质量为m的人正用水平方向的恒定推力F向前推车厢,在车以加速度a向前行驶距离L的过程中,下列说法正确的是( )
A.人对车的推力F做的功为FL
B.人对车做的功为maL
C.车对人的作用力大小为ma
D.车对人的摩擦力做的功为(F-ma)L
14.一辆汽车在平直的公路上由静止开始启动。在启动过程中,汽车牵引力的功率及其瞬时速度随时间的变化情况分别如图甲、乙所示。已知汽车所受阻力恒为重力的0.1倍,重力加速度g取10 m/s2。下列说法正确的是( )
甲 乙
A.该汽车的质量为3 000 kg
B.v0=7.5 m/s
C.在前5 s内,阻力对汽车所做的功为-50 kJ
D.在0~15 s内,牵引力对汽车做功250 kJ
15.汽车发动机的额定功率为60 kW,汽车的质量为4吨,当它行驶在坡度为α(sin α=0.02)的长直公路上时,如图所示,所受摩擦力为车重力的(g取10 m/s2),求:(结果均保留三位有效数字)
(1)汽车所能达到的最大速度vm;
(2)若汽车从静止开始以0.6 m/s2的加速度做匀加速直线运动,则此过程能维持多长时间;
(3)在汽车从静止开始以0.6 m/s2的加速度匀加速行驶的过程中,汽车做功为多少。
16.汽车发动机的额定功率为30 kW,质量为2 000 kg,当汽车在水平路面上行驶时受到的阻力为车重的0.1(g取10 m/s2)倍。求:
(1)汽车在路面上能达到的最大速度;
(2)当汽车速度为10 m/s时的加速度大小;
(3)若汽车从静止开始保持1 m/s2的加速度做匀加速直线运动,则这一过程能持续多长时间?
17.如图所示,水平的传送带以速度 v=6 m/s顺时针运转,两传动轮M、N之间的距离为L=10 m,若在M轮的正上方,将一质量为m=3 kg的物体轻放在传送带上,已知物体与传送带之间的动摩擦因数μ=0.3,在物体由M处传送到N处的过程中,传送带对物体的摩擦力做了多少功?(g取10 m/s2)
18.图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。g取10 m/s2,不计额外功。求:
(1)起重机允许输出的最大功率;
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
参考解析
1 C [人随扶梯向上加速运动时,受踏板支持力、静摩擦力(水平向右)和重力作用,人处于超重状态。支持力大于重力,故A、B错误;支持力与位移方向夹角小于90°,故支持力对人做正功,C正确,D错误。]
2 A [恒力做的功W=Flcos α,比较F、l、α三量即可。由题意知,F1=F2,l1=l2,α1=α2,又W=Flcos α,故无论水平面光滑还是粗糙,均有W1=W2,故A正确。]
3 D [对木块,由牛顿第二定律F=ma,可得加速度为a=,则0~t1时间内的位移为l=at=
根据功的定义可知WF=Fl=]
4 A [A对,B错:功率是表示力做功快慢的物理量,功是表示做功多少的物理量。
C错:P=是功率的定义式,功率与时间没有决定关系,不能说功率与时间成反比。
D错:由于P=Fvcos θ,所以当θ=90°时,功率P为0。]
5 B [设人和车的总质量约为60 kg,假若匀速运动,则人做功时的动力约为F=F阻=12 N,骑行速度约为20 km/h≈5.6 m/s,则人做功的功率P=Fv=67.2 W,选项B最接近题意。]
6 C [物体2 s下落的高度为h=gt2=20 m,落地的竖直分速度为vy=gt=20 m/s,所以落到地面前的瞬间重力的瞬时功率是P=mgvy=400 W,下落过程中重力的平均功率是==200 W,选项C正确。]
7 D [当汽车做匀速运动时速度最大,此时汽车的牵引力F=mgsin θ+kmg,而P=Fvm,由此可得vm=,故选项D正确。]
8 B [汽车匀速行驶时牵引力等于阻力,功率减小一半时,速度不会突变,据P=Fv知,牵引力减小一半,合力跟运动方向相反,汽车做减速运动。汽车速度减小后,的功率不变,则牵引力增大,合力减小,加速度减小,使汽车做加速度不断减小的减速运动,当牵引力增大到与阻力相等时,加速度减为零,汽车重新做匀速直线运动。]
9 B [A图中,拉力竖直向上,并且包在拉力方向上移动了距离,拉力做了功;B图中,拉力竖直向上,而包在水平方向上移动了距离,所以拉力不做功;C图中,拉力竖直向上,并且包在拉力的方向上移动了距离,所以拉力做了功;D图中,拉力竖直向上,小新上楼的过程中包也在竖直方向上移动了距离,所以拉力对包做了功。本题选拉力没有做功的,故选B。]
10 D [功率是描述做功快慢的物理量,功率大说明单位时间内做功多,时间不确定时,某个力对物体做功多,它的功率不一定大,故A错误;由P=,可以知道做功一定时,功率与时间成反比,故B错误;从公式P=Fv,可以知道F不为零,v也不为零,但F与v的方向垂直,此时功率为零,故C错误;功率是描述做功快慢的物理量,所以某个力对物体做功越快,它的功率一定越大,故D正确。]
11 C [根据汽车做匀速直线运动可得此时汽车的牵引力等于阻力,即F=f=1.8×103 N,此时汽车发动机的实际输出功率即瞬时功率,根据P=Fv,代入数据解得此时汽车发动机的实际输出功率为36 kW,A、B、D项均错误,C项正确。]
12 C [支持力和重力与位移垂直,不做功,A、B错误;拉力和摩擦力做功分别为W1=Fscos θ,W2=-μ(mg-Fsin θ)s,C正确,D错误。]
13 A [根据功的公式可知,人对车的推力做功W=FL,A正确;在水平方向上,由牛顿第二定律可知车对人的作用力为F′=ma,人对车的作用力为-ma,故人对车做的功为W′=-maL,B错误;在水平方向上车对人的作用力的合力为ma,而车对人还有支持力,故车对人的作用力为F合==m,C错误;对人由牛顿第二定律可知f-F=ma,f=ma+F,车对人的摩擦力做的功为Wf=fL=(F+ma)L,D错误。]
14 D [由题图乙可得,汽车匀加速阶段的加速度为a==1 m/s2,汽车匀加速阶段的牵引力为F== N=4 000 N,匀加速阶段由牛顿第二定律得F-0.1mg=ma,解得m=2 000 kg,故A错误;牵引力功率为20 kW时,汽车行驶的最大速度为v0== m/s=10 m/s,故B错误;前5 s内汽车的位移为x=at2=12.5 m,阻力做功为Wf=-0.1mgx=-25 kJ,故C错误;0~5 s内牵引力对汽车做功WF1=Fx=4 000×12.5 J=50 kJ,5~15 s内牵引力对汽车做功WF2=Pt=20 000×10 J=200 kJ,在0~15 s内,牵引力对汽车做功250 kJ,故D正确。]
15 [答案] (1)12.5 m/s (2)13.9 s (3)4.16×105 J
[解析] (1)汽车在坡度为α的长直公路上行驶,所受阻力由两部分构成,
即F阻=kmg+mgsin α=4 800 N
又因为F=F阻时,P=F·vm,
所以vm== m/s=12.5 m/s。
(2)汽车从静止开始,以a=0.6 m/s2的加速度匀加速行驶,有F′-kmg-mgsin α=ma,所以F′=ma+kmg+mgsin α=4×103×0.6 N+4 800 N=7.2×103 N;保持这一牵引力,汽车可达到匀加速行驶的最大速度vm′,有vm′== m/s=8.33 m/s
由运动学规律可得t== s=13.9 s。
(3)汽车在匀加速阶段行驶时做功为W=F′·l=F′·=7.2×103×57.82 J=4.16×105 J。
16 [答案] (1)15 m/s (2)0.5 m/s2 (3)7.5 s
[解析] (1)汽车有最大速度时,此时牵引力与阻力平衡,
由此可得:P=F牵·vm=f·vm
所以
vm== m/s=15 m/s。
(2)当速度v=10 m/s时,
F′牵== N=3×103 N
所以a==0.5 m/s2。
(3)若汽车从静止做匀加速直线运动,则当P=P额时,匀加速运动结束,
所以P额=F牵·v,又因为F牵-f=ma′
所以v==
所以t===7.5 s。
17 [答案] 54 J
[解析] 物体放在传送带上后的加速度
a===μg=3 m/s2
设一段时间后物体的速度增大到v=6 m/s,此后物体与传送带速度相同,二者之间不再相对滑动,滑动摩擦力随之消失,可见滑动摩擦力的作用时间为
t== s=2 s
在这2 s内物体水平向右运动的位移为
l=at2=×3×22 m=6 m<L=10 m
故滑动摩擦力对物体所做的功为
W=Fl=μmgl=0.3×3×10×6 J=54 J。
18 [答案] (1)5.1×104 W (2)5 s 2.04×104 W
[解析] (1)设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力。则由P0=F0vm知 ①
P0=mgvm ②
代入数据,有P0=5.1×104 W。 ③
(2)匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:P0=Fv1 ④
F-mg=ma ⑤
v1=at1 ⑥
由③④⑤⑥,代入数据,得t1=5 s ⑦
t=2 s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则v2=at ⑧
P=Fv2 ⑨
由⑤⑧⑨,代入数据,得P=2.04×104 W。
1.功与功率
1.如图所示,稳站在商店自动扶梯水平踏板上的人,随扶梯斜向上做加速运动,则在此过程中( )
A.人只受到重力和踏板的支持力作用
B.人受到的重力和踏板的支持力大小相等方向相反
C.支持力对人做正功
D.支持力对人做功为零
2.如图甲、乙所示,质量分别为M和m的两物块,M>m,分别在同样大小的恒力F作用下,沿水平面由静止开始做直线运动,F与水平面的夹角相同。经过相同的位移,设F对M做的功为W1,对m做的功为W2,则( )
甲 乙
A.无论水平面光滑与否,都有W1=W2
B.若水平面光滑,则W1>W2
C.若水平面粗糙,则W1>W2
D.若水平面粗糙,则W1<W2
3.质量为m的木块静止在光滑的水平地面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在0~t1时间内力F做的功是( )
A. B. C. D.
4.关于功率的概念,下列说法中正确的是( )
A.功率是表示力做功快慢的物理量
B.功率是表示力做功多少的物理量
C.由P=可知,功率与时间成反比
D.只要F不为零,v也不为零,这个力的功率P就一定不为零
5.为了响应公共交通出行的环保倡议,小明骑公共自行车上下班。假设在平直公路上自行车所受阻力约为车和人总重的,则小明以正常速度骑行时的功率最接近于( )
A.1 W B.100 W
C.10 kW D.100 kW
6.如图所示,质量为2 kg的物体以10 m/s的初速度水平抛出,经过2 s 落地。g取10 m/s2。关于重力做功的功率,下列说法正确的是( )
A.下落过程中重力的平均功率是400 W
B.下落过程中重力的平均功率是100 W
C.落地前的瞬间重力的瞬时功率是400 W
D.落地前的瞬间重力的瞬时功率是200 W
7.质量为m的汽车,其发动机额定功率为P。当它开上一个倾角为θ的斜坡时,受到的摩擦阻力为车重力的k倍,则车的最大速度为( )
A. B.
C. D.
8.汽车在平直公路上以速度v0匀速行驶,发动机功率为P,快进入闹市区时,司机减小了油门,使汽车的功率立即减小为,并保持此功率继续在平直公路上行驶。设汽车行驶时所受的阻力恒定,则能正确反映从减小油门开始汽车的速度随时间变化的图像是( )
A B
C D
9.如图所示是小新提包回家的情景,小新提包的拉力没有做功的是( )
A.将包提起来 B.站在水平匀速行驶的车上
C.乘升降电梯 D.提着包上楼
10.关于功率的概念,下列说法正确的是( )
A.力对物体做功越多,则力做功的功率越大
B.由P=可知,功率与时间成反比
C.从P=Fv可知,只要F不为零,v也不为零,那么功率P就一定不为零
D.某个力对物体做功越快,它的功率一定越大
11.质量为1.5×103 kg的汽车在水平路面上匀速行驶,速度为20 m/s,受到的阻力大小为1.8×103 N。此时,汽车发动机输出的实际功率是( )
A.90 W B.30 kW
C.36 kW D.300 kW
12.如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离s。已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )
A.支持力做功为mgs
B.重力做功为mgs
C.拉力做功为Fscos θ
D.滑动摩擦力做功为-μmgs
13.如图所示,水平路面上有一辆质量为M的汽车,车厢中有一个质量为m的人正用水平方向的恒定推力F向前推车厢,在车以加速度a向前行驶距离L的过程中,下列说法正确的是( )
A.人对车的推力F做的功为FL
B.人对车做的功为maL
C.车对人的作用力大小为ma
D.车对人的摩擦力做的功为(F-ma)L
14.一辆汽车在平直的公路上由静止开始启动。在启动过程中,汽车牵引力的功率及其瞬时速度随时间的变化情况分别如图甲、乙所示。已知汽车所受阻力恒为重力的0.1倍,重力加速度g取10 m/s2。下列说法正确的是( )
甲 乙
A.该汽车的质量为3 000 kg
B.v0=7.5 m/s
C.在前5 s内,阻力对汽车所做的功为-50 kJ
D.在0~15 s内,牵引力对汽车做功250 kJ
15.汽车发动机的额定功率为60 kW,汽车的质量为4吨,当它行驶在坡度为α(sin α=0.02)的长直公路上时,如图所示,所受摩擦力为车重力的(g取10 m/s2),求:(结果均保留三位有效数字)
(1)汽车所能达到的最大速度vm;
(2)若汽车从静止开始以0.6 m/s2的加速度做匀加速直线运动,则此过程能维持多长时间;
(3)在汽车从静止开始以0.6 m/s2的加速度匀加速行驶的过程中,汽车做功为多少。
16.汽车发动机的额定功率为30 kW,质量为2 000 kg,当汽车在水平路面上行驶时受到的阻力为车重的0.1(g取10 m/s2)倍。求:
(1)汽车在路面上能达到的最大速度;
(2)当汽车速度为10 m/s时的加速度大小;
(3)若汽车从静止开始保持1 m/s2的加速度做匀加速直线运动,则这一过程能持续多长时间?
17.如图所示,水平的传送带以速度 v=6 m/s顺时针运转,两传动轮M、N之间的距离为L=10 m,若在M轮的正上方,将一质量为m=3 kg的物体轻放在传送带上,已知物体与传送带之间的动摩擦因数μ=0.3,在物体由M处传送到N处的过程中,传送带对物体的摩擦力做了多少功?(g取10 m/s2)
18.图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。g取10 m/s2,不计额外功。求:
(1)起重机允许输出的最大功率;
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
参考解析
1 C [人随扶梯向上加速运动时,受踏板支持力、静摩擦力(水平向右)和重力作用,人处于超重状态。支持力大于重力,故A、B错误;支持力与位移方向夹角小于90°,故支持力对人做正功,C正确,D错误。]
2 A [恒力做的功W=Flcos α,比较F、l、α三量即可。由题意知,F1=F2,l1=l2,α1=α2,又W=Flcos α,故无论水平面光滑还是粗糙,均有W1=W2,故A正确。]
3 D [对木块,由牛顿第二定律F=ma,可得加速度为a=,则0~t1时间内的位移为l=at=
根据功的定义可知WF=Fl=]
4 A [A对,B错:功率是表示力做功快慢的物理量,功是表示做功多少的物理量。
C错:P=是功率的定义式,功率与时间没有决定关系,不能说功率与时间成反比。
D错:由于P=Fvcos θ,所以当θ=90°时,功率P为0。]
5 B [设人和车的总质量约为60 kg,假若匀速运动,则人做功时的动力约为F=F阻=12 N,骑行速度约为20 km/h≈5.6 m/s,则人做功的功率P=Fv=67.2 W,选项B最接近题意。]
6 C [物体2 s下落的高度为h=gt2=20 m,落地的竖直分速度为vy=gt=20 m/s,所以落到地面前的瞬间重力的瞬时功率是P=mgvy=400 W,下落过程中重力的平均功率是==200 W,选项C正确。]
7 D [当汽车做匀速运动时速度最大,此时汽车的牵引力F=mgsin θ+kmg,而P=Fvm,由此可得vm=,故选项D正确。]
8 B [汽车匀速行驶时牵引力等于阻力,功率减小一半时,速度不会突变,据P=Fv知,牵引力减小一半,合力跟运动方向相反,汽车做减速运动。汽车速度减小后,的功率不变,则牵引力增大,合力减小,加速度减小,使汽车做加速度不断减小的减速运动,当牵引力增大到与阻力相等时,加速度减为零,汽车重新做匀速直线运动。]
9 B [A图中,拉力竖直向上,并且包在拉力方向上移动了距离,拉力做了功;B图中,拉力竖直向上,而包在水平方向上移动了距离,所以拉力不做功;C图中,拉力竖直向上,并且包在拉力的方向上移动了距离,所以拉力做了功;D图中,拉力竖直向上,小新上楼的过程中包也在竖直方向上移动了距离,所以拉力对包做了功。本题选拉力没有做功的,故选B。]
10 D [功率是描述做功快慢的物理量,功率大说明单位时间内做功多,时间不确定时,某个力对物体做功多,它的功率不一定大,故A错误;由P=,可以知道做功一定时,功率与时间成反比,故B错误;从公式P=Fv,可以知道F不为零,v也不为零,但F与v的方向垂直,此时功率为零,故C错误;功率是描述做功快慢的物理量,所以某个力对物体做功越快,它的功率一定越大,故D正确。]
11 C [根据汽车做匀速直线运动可得此时汽车的牵引力等于阻力,即F=f=1.8×103 N,此时汽车发动机的实际输出功率即瞬时功率,根据P=Fv,代入数据解得此时汽车发动机的实际输出功率为36 kW,A、B、D项均错误,C项正确。]
12 C [支持力和重力与位移垂直,不做功,A、B错误;拉力和摩擦力做功分别为W1=Fscos θ,W2=-μ(mg-Fsin θ)s,C正确,D错误。]
13 A [根据功的公式可知,人对车的推力做功W=FL,A正确;在水平方向上,由牛顿第二定律可知车对人的作用力为F′=ma,人对车的作用力为-ma,故人对车做的功为W′=-maL,B错误;在水平方向上车对人的作用力的合力为ma,而车对人还有支持力,故车对人的作用力为F合==m,C错误;对人由牛顿第二定律可知f-F=ma,f=ma+F,车对人的摩擦力做的功为Wf=fL=(F+ma)L,D错误。]
14 D [由题图乙可得,汽车匀加速阶段的加速度为a==1 m/s2,汽车匀加速阶段的牵引力为F== N=4 000 N,匀加速阶段由牛顿第二定律得F-0.1mg=ma,解得m=2 000 kg,故A错误;牵引力功率为20 kW时,汽车行驶的最大速度为v0== m/s=10 m/s,故B错误;前5 s内汽车的位移为x=at2=12.5 m,阻力做功为Wf=-0.1mgx=-25 kJ,故C错误;0~5 s内牵引力对汽车做功WF1=Fx=4 000×12.5 J=50 kJ,5~15 s内牵引力对汽车做功WF2=Pt=20 000×10 J=200 kJ,在0~15 s内,牵引力对汽车做功250 kJ,故D正确。]
15 [答案] (1)12.5 m/s (2)13.9 s (3)4.16×105 J
[解析] (1)汽车在坡度为α的长直公路上行驶,所受阻力由两部分构成,
即F阻=kmg+mgsin α=4 800 N
又因为F=F阻时,P=F·vm,
所以vm== m/s=12.5 m/s。
(2)汽车从静止开始,以a=0.6 m/s2的加速度匀加速行驶,有F′-kmg-mgsin α=ma,所以F′=ma+kmg+mgsin α=4×103×0.6 N+4 800 N=7.2×103 N;保持这一牵引力,汽车可达到匀加速行驶的最大速度vm′,有vm′== m/s=8.33 m/s
由运动学规律可得t== s=13.9 s。
(3)汽车在匀加速阶段行驶时做功为W=F′·l=F′·=7.2×103×57.82 J=4.16×105 J。
16 [答案] (1)15 m/s (2)0.5 m/s2 (3)7.5 s
[解析] (1)汽车有最大速度时,此时牵引力与阻力平衡,
由此可得:P=F牵·vm=f·vm
所以
vm== m/s=15 m/s。
(2)当速度v=10 m/s时,
F′牵== N=3×103 N
所以a==0.5 m/s2。
(3)若汽车从静止做匀加速直线运动,则当P=P额时,匀加速运动结束,
所以P额=F牵·v,又因为F牵-f=ma′
所以v==
所以t===7.5 s。
17 [答案] 54 J
[解析] 物体放在传送带上后的加速度
a===μg=3 m/s2
设一段时间后物体的速度增大到v=6 m/s,此后物体与传送带速度相同,二者之间不再相对滑动,滑动摩擦力随之消失,可见滑动摩擦力的作用时间为
t== s=2 s
在这2 s内物体水平向右运动的位移为
l=at2=×3×22 m=6 m<L=10 m
故滑动摩擦力对物体所做的功为
W=Fl=μmgl=0.3×3×10×6 J=54 J。
18 [答案] (1)5.1×104 W (2)5 s 2.04×104 W
[解析] (1)设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力。则由P0=F0vm知 ①
P0=mgvm ②
代入数据,有P0=5.1×104 W。 ③
(2)匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:P0=Fv1 ④
F-mg=ma ⑤
v1=at1 ⑥
由③④⑤⑥,代入数据,得t1=5 s ⑦
t=2 s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则v2=at ⑧
P=Fv2 ⑨
由⑤⑧⑨,代入数据,得P=2.04×104 W。
