8.4 机械能守恒定律 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案)
文档属性
| 名称 | 8.4 机械能守恒定律 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-11 08:06:16 | ||
图片预览




文档简介
第八章 机械能守恒定律
4.机械能守恒定律
1.奥运会比赛项目撑竿跳高如图所示,下列说法不正确的是( )
A.加速助跑过程中,运动员的动能增加
B.起跳上升过程中,竿的弹性势能一直增加
C.起跳上升过程中,运动员的重力势能增加
D.越过横竿后下落过程中,运动员的重力势能减少动能增加
2.下列关于机械能守恒的说法正确的是( )
A.物体匀速向上运动时所受合力为零,其机械能守恒
B.物体做平抛运动时机械能守恒
C.物体在竖直平面内做匀速圆周运动时机械能守恒
D.物体沿粗糙斜面加速下滑时机械能守恒
3 .如图所示,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最大时对应的轨道半径为(重力加速度为g)( )
A. B. C. D.
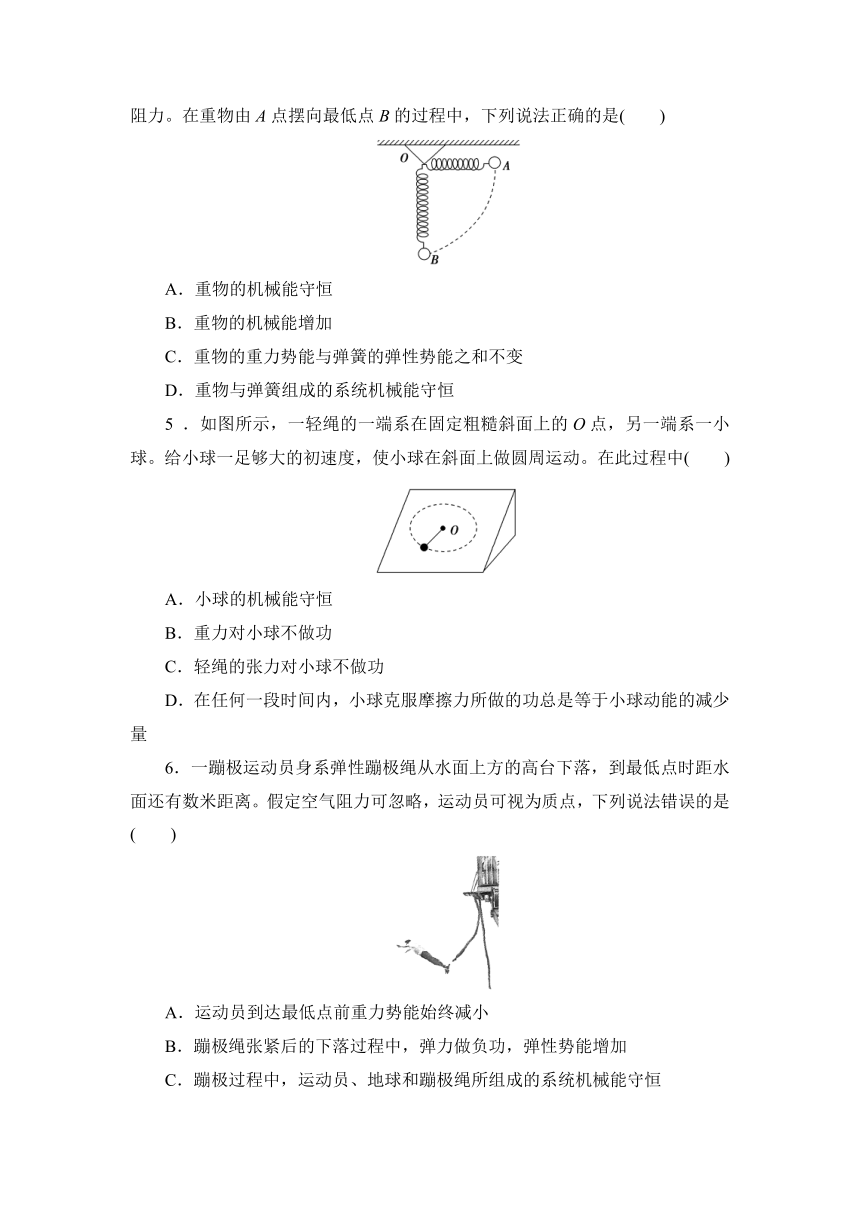
4 .如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度地释放,让它自由摆下,不计空气阻力。在重物由A点摆向最低点B的过程中,下列说法正确的是( )
A.重物的机械能守恒
B.重物的机械能增加
C.重物的重力势能与弹簧的弹性势能之和不变
D.重物与弹簧组成的系统机械能守恒
5 .如图所示,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球。给小球一足够大的初速度,使小球在斜面上做圆周运动。在此过程中( )
A.小球的机械能守恒
B.重力对小球不做功
C.轻绳的张力对小球不做功
D.在任何一段时间内,小球克服摩擦力所做的功总是等于小球动能的减少量
6.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离。假定空气阻力可忽略,运动员可视为质点,下列说法错误的是( )
A.运动员到达最低点前重力势能始终减小
B.蹦极绳张紧后的下落过程中,弹力做负功,弹性势能增加
C.蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒
D.蹦极过程中,重力势能的改变量与重力势能参考平面的选取有关
7.一款名叫“跳一跳”的小游戏引起了好多人的兴趣。游戏要求操作者通过控制棋子(质量为m)脱离平台时的速度,使其能从一个平台跳到旁边的平台上。如图所示的抛物线为棋子在某次跳跃过程中的运动轨迹,不计空气阻力。则(重力加速度为g)( )
A.棋子从起跳至运动到最高点的过程中,机械能增加mgh
B.棋子离开平台时的动能为mgh
C.棋子从离开平台至运动到最高点的过程中,重力势能增加mgh
D.棋子落到平台上的速度大小为
8.如图所示,可视为质点的小球A、B用不可伸长的细软轻绳连接,跨过固定在地面上半径为R的光滑圆柱,A的质量为B的两倍。当B位于地面时,A恰与圆柱轴心等高。将A由静止释放,B上升的最大高度是( )
A.2R B. C. D.
9.在如图所示的物理过程示意图中,甲图为一端固定有小球的轻杆,从右偏上30°角的位置释放后小球绕光滑支点摆动;乙图为末端固定有A、B两小球的轻质直角架,释放后绕通过直角顶点的固定轴O无摩擦转动;丙图为置于光滑水平面上的A、B两小车,B静止,A获得一向右的初速度后向右运动,某时刻连接两车的细绳绷紧,然后带动B车运动;丁图为置于光滑水平面上的带有竖直支架的小车,把用细绳悬挂的小球从图示位置释放,小球开始摆动。则关于这几个物理过程(空气阻力忽略不计),下列判断正确的是( )
甲 乙
丙 丁
A.甲图中小球机械能守恒
B.乙图中小球A的机械能守恒
C.丙图中两车组成的系统机械能守恒
D.丁图中小球的机械能守恒
10.有一竖直放置的“T”形架,表面光滑,滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻细绳相连,A的质量是B质量的6倍,A、B均可看成质点,如图所示,开始时细绳水平伸直,A、B静止。由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v,则连接A、B的绳长为( )
A. B. C. D.
11.如图所示,上表面有一段光滑圆弧且质量为M的小车A置于光滑水平面上。在一质量为m的物体B自圆弧上端自由滑下的同时释放A,则( )
A.在B下滑的过程中,B的机械能守恒
B.轨道对B的支持力对B不做功
C.在B下滑的过程中,A和地球组成的系统的机械能守恒
D.A、B和地球组成的系统的机械能守恒
12.一物体由h高处自由落下,以地面为参考平面,当物体的动能等于势能时,物体经历的时间为( )
A. B. C. D.以上都不对
13.以相同大小的初速度v0将物体从同一水平面分别竖直上抛、斜上抛、沿光滑斜面(足够长)上滑,如图所示,三种情况达到的最大高度分别为h1、h2和h3,不计空气阻力(斜上抛运动物体在最高点的速度方向水平),则( )
A.h1=h2>h3 B.h1=h2C.h1=h3h2
4.机械能守恒定律
1.奥运会比赛项目撑竿跳高如图所示,下列说法不正确的是( )
A.加速助跑过程中,运动员的动能增加
B.起跳上升过程中,竿的弹性势能一直增加
C.起跳上升过程中,运动员的重力势能增加
D.越过横竿后下落过程中,运动员的重力势能减少动能增加
2.下列关于机械能守恒的说法正确的是( )
A.物体匀速向上运动时所受合力为零,其机械能守恒
B.物体做平抛运动时机械能守恒
C.物体在竖直平面内做匀速圆周运动时机械能守恒
D.物体沿粗糙斜面加速下滑时机械能守恒
3 .如图所示,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最大时对应的轨道半径为(重力加速度为g)( )
A. B. C. D.
4 .如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度地释放,让它自由摆下,不计空气阻力。在重物由A点摆向最低点B的过程中,下列说法正确的是( )
A.重物的机械能守恒
B.重物的机械能增加
C.重物的重力势能与弹簧的弹性势能之和不变
D.重物与弹簧组成的系统机械能守恒
5 .如图所示,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球。给小球一足够大的初速度,使小球在斜面上做圆周运动。在此过程中( )
A.小球的机械能守恒
B.重力对小球不做功
C.轻绳的张力对小球不做功
D.在任何一段时间内,小球克服摩擦力所做的功总是等于小球动能的减少量
6.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离。假定空气阻力可忽略,运动员可视为质点,下列说法错误的是( )
A.运动员到达最低点前重力势能始终减小
B.蹦极绳张紧后的下落过程中,弹力做负功,弹性势能增加
C.蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒
D.蹦极过程中,重力势能的改变量与重力势能参考平面的选取有关
7.一款名叫“跳一跳”的小游戏引起了好多人的兴趣。游戏要求操作者通过控制棋子(质量为m)脱离平台时的速度,使其能从一个平台跳到旁边的平台上。如图所示的抛物线为棋子在某次跳跃过程中的运动轨迹,不计空气阻力。则(重力加速度为g)( )
A.棋子从起跳至运动到最高点的过程中,机械能增加mgh
B.棋子离开平台时的动能为mgh
C.棋子从离开平台至运动到最高点的过程中,重力势能增加mgh
D.棋子落到平台上的速度大小为
8.如图所示,可视为质点的小球A、B用不可伸长的细软轻绳连接,跨过固定在地面上半径为R的光滑圆柱,A的质量为B的两倍。当B位于地面时,A恰与圆柱轴心等高。将A由静止释放,B上升的最大高度是( )
A.2R B. C. D.
9.在如图所示的物理过程示意图中,甲图为一端固定有小球的轻杆,从右偏上30°角的位置释放后小球绕光滑支点摆动;乙图为末端固定有A、B两小球的轻质直角架,释放后绕通过直角顶点的固定轴O无摩擦转动;丙图为置于光滑水平面上的A、B两小车,B静止,A获得一向右的初速度后向右运动,某时刻连接两车的细绳绷紧,然后带动B车运动;丁图为置于光滑水平面上的带有竖直支架的小车,把用细绳悬挂的小球从图示位置释放,小球开始摆动。则关于这几个物理过程(空气阻力忽略不计),下列判断正确的是( )
甲 乙
丙 丁
A.甲图中小球机械能守恒
B.乙图中小球A的机械能守恒
C.丙图中两车组成的系统机械能守恒
D.丁图中小球的机械能守恒
10.有一竖直放置的“T”形架,表面光滑,滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻细绳相连,A的质量是B质量的6倍,A、B均可看成质点,如图所示,开始时细绳水平伸直,A、B静止。由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v,则连接A、B的绳长为( )
A. B. C. D.
11.如图所示,上表面有一段光滑圆弧且质量为M的小车A置于光滑水平面上。在一质量为m的物体B自圆弧上端自由滑下的同时释放A,则( )
A.在B下滑的过程中,B的机械能守恒
B.轨道对B的支持力对B不做功
C.在B下滑的过程中,A和地球组成的系统的机械能守恒
D.A、B和地球组成的系统的机械能守恒
12.一物体由h高处自由落下,以地面为参考平面,当物体的动能等于势能时,物体经历的时间为( )
A. B. C. D.以上都不对
13.以相同大小的初速度v0将物体从同一水平面分别竖直上抛、斜上抛、沿光滑斜面(足够长)上滑,如图所示,三种情况达到的最大高度分别为h1、h2和h3,不计空气阻力(斜上抛运动物体在最高点的速度方向水平),则( )
A.h1=h2>h3 B.h1=h2
h2
14.如图所示,质量为m和3m的小球A和B,系在长为L的细线两端,桌面水平光滑,高为h(hA. B.
C. D.
15.如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上。若以地面为零势能面,不计空气阻力,则下列说法中正确的是( )
A.物体到海平面时的重力势能为mgh
B.物体到海平面之前任一位置机械能为mv-mgh
C.物体在海平面上的动能为mv+mgh
D.物体在海平面上的机械能为mv+mgh
16.如图所示,轻弹簧一端与墙相连处于自然状态,质量为4 kg的木块沿光滑的水平面以5 m/s的速度运动并开始挤压弹簧,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
17.竖直向上抛出质量为0.1 kg的石头,石头上升过程中,空气阻力忽略不计,石头离手时的速度v0=20 m/s。g取10 m/s2。求:
(1)石头离手时的动能;
(2)石头能够上升的最大高度;
(3)石头离开抛出点15 m高处的速度大小。
18.滑板运动是一种陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行。如图所示,abcde为同一竖直平面内依次平滑连接的滑行轨道,其中bcd是一段半径R=2.5 m的圆弧轨道,O点为圆心,c点为圆弧轨道的最低点。运动员脚踩滑板从高H=3 m处由静止出发,沿轨道自由滑下。运动员连同滑板可视为质点,其总质量m=60 kg。忽略摩擦阻力和空气阻力,取g=10 m/s2,求运动员滑经c点时轨道对滑板的支持力的大小。
19.如图所示,在足够长的光滑水平桌面上固定一个四分之一光滑圆弧形槽,半径R=0.45 m,末端与桌面相切。将质量m=0.1 kg的小球(可视为质点)由槽的顶端无初速度释放,经桌面上A点水平飞出,小球恰好无碰撞地沿圆弧轨道切线从B点进入固定的竖直光滑圆弧轨道,B、C为圆弧轨道的两端点,其连线水平,O为圆弧轨道的最低点。已知圆弧轨道对应圆心角θ=106°,半径r=1 m。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。求:
(1)小球沿圆弧形槽下滑到槽底端时,小球的速度大小;
(2)桌面离水平地面的高度h;
(3)小球运动至O点时对圆弧轨道的压力大小。
20.如图所示,有一轻质杆可绕O点在竖直平面内自由转动,在杆的另一端和中点各固定一个质量均为m的小球A、B,杆长为L。开始时,杆静止在水平位置,则无初速度释放后杆转到竖直位置时,求A、B两小球的速度。
21.如图所示,质量为m的物体,以某一初速度从A点向下沿光滑的轨道运动,不计空气阻力,若物体通过轨道最低点B时的速度为3,求:
(1)物体在A点时的速度大小;
(2)物体离开C点后还能上升的高度。
参考解析
1 B [加速助跑过程中速度增大,动能增加,A对;撑竿从开始形变到撑竿恢复形变时,先是运动员部分动能转化为竿的弹性势能,后弹性势能转化为运动员的动能与重力势能,竿的弹性势能不是一直增加,B错;起跳上升过程中,运动员的高度在不断增加,所以运动员的重力势能增加,C对;当运动员越过横竿下落的过程中,他的高度降低、速度增大,重力势能转化为动能,即重力势能减少,动能增加,D对。]
2 B [物体向上匀速运动,动能不变,重力势能增加,故机械能增加,A错;物体做平抛运动时,只有重力做功,机械能守恒,B对;物体在竖直平面内做匀速圆周运动过程中,动能不变,势能变化,故机械能不守恒,C错;物体沿粗糙斜面下滑时,除重力做功外,还有摩擦力做功,机械能不守恒,D错。]
3 B [根据机械能守恒定律有mv2=mv+mg·2R,根据平抛运动的规律有x=v0t,2R=gt2,联立整理可得x=,结合数学知识,当R=时,水平距离最大,选项B正确。]
4 D [重物由A点摆到B点的过程中,弹簧被拉长,弹簧的弹力对重物做了负功,所以重物的机械能减少,故选项A、B错误;此过程中,由于只有重力和弹簧的弹力做功,所以重物与弹簧组成的系统机械能守恒,即重物减少的重力势能,等于重物获得的动能与弹簧的弹性势能之和,故选项C错误,D正确。]
5 C [斜面粗糙,小球受到重力、支持力、摩擦力、轻绳张力的作用,由于除重力做功外,支持力和轻绳张力总是与运动方向垂直,故不做功,摩擦力做负功,机械能减少,A、B错误,C正确;小球动能的变化量等于合外力对其做的功,即重力与摩擦力做功的代数和,D错误。]
6 D [运动员到达最低点前重力始终做正功,重力势能始终减小,A对;蹦极绳张紧后的下落过程中,弹力方向与位移方向始终相反,弹力做负功,弹性势能增加,B对;在运动员、地球和蹦极绳所组成的系统中,只有重力和弹力做功,则系统的机械能守恒,C对;重力势能的改变量与重力做功有关,取决于初末位置的高度差,与重力势能参考平面的选取无关,D错。]
7 C [棋子起跳后只受重力作用,机械能守恒,A错;棋子在最高点具有水平方向的速度,所以离开平台时的动能大于mgh,落到平台上的速度要大于,B、D错;棋子从离开平台至运动到最高点过程中重力做功为WG=-mgh,所以重力势能增加mgh,C对。]
8 C [A、B的质量分别记为2m、m,当A落到地面上时,B恰好运动到与圆柱轴心等高处,以A、B整体为研究对象,则A、B组成的系统机械能守恒,故有2mgR-mgR=(2m+m)v2,A落到地面上以后,B以速度v竖直上抛,上升的高度为h′=,解得h′=R,此时绳子未绷直,故B上升的最大高度为R+h′=R,选项C正确。]
9 A [甲图中轻杆对小球不做功,小球的机械能守恒;乙图中A、B两球通过杆相互影响(例如开始时A球带动B球转动),轻杆对A的弹力不沿杆的方向,会对小球做功,所以每个小球的机械能不守恒,但把两个小球作为一个系统时系统的机械能守恒;丙图中细绳绷紧的过程虽然只有弹力作为内力做功,但弹力突变有内能转化,机械能不守恒;丁图中细绳会拉动小车运动,取地面为参考系,小球的运动轨迹不是圆弧,细绳会对小球做功,小球的机械能不守恒,把小球和小车当作一个系统,机械能才守恒。]
10 B [将A、B的速度分解为沿绳的方向和垂直于绳的方向,两滑块沿绳方向的速度相等,有vBcos 60°=vAcos 30°,所以vA=v,设A的质量为6m,B的质量为m;A、B组成的系统机械能守恒,有mgh=×6mv+mv2,所以有h=,绳长l=2h=,故B正确,A、C、D错误。]
11 D [B下滑时对A有压力,A对B有支持力。A向左滑动,水平方向发生位移,B对A做正功,A对B做负功。因而A、B各自的机械能不守恒,A、B、C错;A、B和地球组成的系统没有与外界发生机械能的转移,也没有摩擦,机械能没有转化为其他形式的能,系统的机械能守恒,D对。]
12 B [设物体动能等于势能时速度为v,根据机械能守恒mv2+Ep=mgh,又mv2=Ep,解得v=,而物体做自由落体运动,v=gt,解得t=,B正确。]
13 D [竖直上抛和沿斜面运动的物体,上升到最高点时,速度均为0,由机械能守恒得mgh=mv,所以h=,斜上抛运动物体在最高点速度不为零,设为v1,则mgh2=mv-mv,所以h214 A [A球落地之前,对于A、B组成的系统,只有重力做功,系统的机械能守恒,则有mgh=(m+3m)v2,解得v=,A球落地后,B球做匀速直线运动,故B球离开桌面时的速度仍为,选项A正确。]
15 C [物体到达海平面时位于参考平面以下,重力势能为-mgh,A错误;物体运动过程中,只有重力做功,机械能为mv,B、D错误;根据机械能守恒定律,可知物体在海平面上的动能Ek=mv2=mgh+mv,C正确。]
16[答案] (1)50 J (2)32 J
[解析] (1)木块压缩弹簧的过程中,木块和弹簧组成的系统机械能守恒,弹性势能最大时,对应木块的动能为零,故有
Epm=mv=×4×52 J=50 J。
(2)由机械能守恒有
mv=Ep1+mv
×4×52 J=Ep1+×4×32 J
得Ep1=32 J。
17 [答案] (1)20 J (2)20 m (3)10 m/s
[解析] (1)根据动能的表达式得Ek=mv=×0.1×202 J=20 J。
(2)根据机械能守恒定律mv=mgH,
解得H=20 m。
(3)根据机械能守恒定律,选抛出点为重力势能参考平面得mv=mv2+mgh,
解得v=10 m/s。
18[答案] 2 040 N
[解析] 运动员从开始滑下至c点,
由机械能守恒定律得mgH=mv2 ①
运动员滑至最低点时,由牛顿运动定律和向心力公式得N-mg=m ②
由①②得N=mg=2 040 N。
19[答案] (1)3 m/s (2)0.8 m (3)4.3 N
[解析] (1)小球沿圆弧形槽下滑到槽底端过程中机械能守恒,有
mgR=mv
解得v1=3 m/s。
(2)小球离开桌面后以3 m/s的初速度做平抛运动,竖直方向有
h=gt2,
小球恰好无碰撞地沿圆弧轨道切线从B点进入固定的竖直光滑圆弧轨道,则tan 53°=,
解得t=0.4 s,h=0.8 m。
(3)小球由A点到O点,由机械能守恒定律得
mg(h+r-rcos 53°)=mv-mv,
在O点,由牛顿第二定律得F-mg=m,
代入数据解得F=4.3 N,
根据牛顿第三定律,小球运动至O点时对圆弧轨道的压力大小为4.3 N。
20[答案]
[解析] 把A、B两小球和杆看成一个系统,杆对A、B两小球的弹力为系统的内力,对系统而言,只有重力做功,系统的机械能守恒。以A球在最低点的位置为零势能位置,则初状态:系统的动能为Ek1=0,重力势能为Ep1=2mgL,
末状态(即到竖直位置):
系统的动能为Ek2=mv+mv,
重力势能为Ep2=mg,
由机械能守恒定律得2mgL=mgL+mv+mv,
又因为在自由转动过程中A、B两球的角速度相同,则vA=2vB,
联立解得vA=,vB=。
21 [答案] (1) (2)3.5R
[解析] (1)物体在运动的全过程中只有重力做功,机械能守恒,选取B点为零势能点。设物体在B处的速度为vB,则mg·3R+mv=mv,
得v0=。
(2)设从B点上升到最高点的高度为HB,由机械能守恒可得mgHB=mv,HB=4.5R
所以离开C点后还能上升HC=HB-R=3.5R。
C. D.
15.如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上。若以地面为零势能面,不计空气阻力,则下列说法中正确的是( )
A.物体到海平面时的重力势能为mgh
B.物体到海平面之前任一位置机械能为mv-mgh
C.物体在海平面上的动能为mv+mgh
D.物体在海平面上的机械能为mv+mgh
16.如图所示,轻弹簧一端与墙相连处于自然状态,质量为4 kg的木块沿光滑的水平面以5 m/s的速度运动并开始挤压弹簧,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
17.竖直向上抛出质量为0.1 kg的石头,石头上升过程中,空气阻力忽略不计,石头离手时的速度v0=20 m/s。g取10 m/s2。求:
(1)石头离手时的动能;
(2)石头能够上升的最大高度;
(3)石头离开抛出点15 m高处的速度大小。
18.滑板运动是一种陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行。如图所示,abcde为同一竖直平面内依次平滑连接的滑行轨道,其中bcd是一段半径R=2.5 m的圆弧轨道,O点为圆心,c点为圆弧轨道的最低点。运动员脚踩滑板从高H=3 m处由静止出发,沿轨道自由滑下。运动员连同滑板可视为质点,其总质量m=60 kg。忽略摩擦阻力和空气阻力,取g=10 m/s2,求运动员滑经c点时轨道对滑板的支持力的大小。
19.如图所示,在足够长的光滑水平桌面上固定一个四分之一光滑圆弧形槽,半径R=0.45 m,末端与桌面相切。将质量m=0.1 kg的小球(可视为质点)由槽的顶端无初速度释放,经桌面上A点水平飞出,小球恰好无碰撞地沿圆弧轨道切线从B点进入固定的竖直光滑圆弧轨道,B、C为圆弧轨道的两端点,其连线水平,O为圆弧轨道的最低点。已知圆弧轨道对应圆心角θ=106°,半径r=1 m。取g=10 m/s2,sin 37°=0.6,cos 37°=0.8。求:
(1)小球沿圆弧形槽下滑到槽底端时,小球的速度大小;
(2)桌面离水平地面的高度h;
(3)小球运动至O点时对圆弧轨道的压力大小。
20.如图所示,有一轻质杆可绕O点在竖直平面内自由转动,在杆的另一端和中点各固定一个质量均为m的小球A、B,杆长为L。开始时,杆静止在水平位置,则无初速度释放后杆转到竖直位置时,求A、B两小球的速度。
21.如图所示,质量为m的物体,以某一初速度从A点向下沿光滑的轨道运动,不计空气阻力,若物体通过轨道最低点B时的速度为3,求:
(1)物体在A点时的速度大小;
(2)物体离开C点后还能上升的高度。
参考解析
1 B [加速助跑过程中速度增大,动能增加,A对;撑竿从开始形变到撑竿恢复形变时,先是运动员部分动能转化为竿的弹性势能,后弹性势能转化为运动员的动能与重力势能,竿的弹性势能不是一直增加,B错;起跳上升过程中,运动员的高度在不断增加,所以运动员的重力势能增加,C对;当运动员越过横竿下落的过程中,他的高度降低、速度增大,重力势能转化为动能,即重力势能减少,动能增加,D对。]
2 B [物体向上匀速运动,动能不变,重力势能增加,故机械能增加,A错;物体做平抛运动时,只有重力做功,机械能守恒,B对;物体在竖直平面内做匀速圆周运动过程中,动能不变,势能变化,故机械能不守恒,C错;物体沿粗糙斜面下滑时,除重力做功外,还有摩擦力做功,机械能不守恒,D错。]
3 B [根据机械能守恒定律有mv2=mv+mg·2R,根据平抛运动的规律有x=v0t,2R=gt2,联立整理可得x=,结合数学知识,当R=时,水平距离最大,选项B正确。]
4 D [重物由A点摆到B点的过程中,弹簧被拉长,弹簧的弹力对重物做了负功,所以重物的机械能减少,故选项A、B错误;此过程中,由于只有重力和弹簧的弹力做功,所以重物与弹簧组成的系统机械能守恒,即重物减少的重力势能,等于重物获得的动能与弹簧的弹性势能之和,故选项C错误,D正确。]
5 C [斜面粗糙,小球受到重力、支持力、摩擦力、轻绳张力的作用,由于除重力做功外,支持力和轻绳张力总是与运动方向垂直,故不做功,摩擦力做负功,机械能减少,A、B错误,C正确;小球动能的变化量等于合外力对其做的功,即重力与摩擦力做功的代数和,D错误。]
6 D [运动员到达最低点前重力始终做正功,重力势能始终减小,A对;蹦极绳张紧后的下落过程中,弹力方向与位移方向始终相反,弹力做负功,弹性势能增加,B对;在运动员、地球和蹦极绳所组成的系统中,只有重力和弹力做功,则系统的机械能守恒,C对;重力势能的改变量与重力做功有关,取决于初末位置的高度差,与重力势能参考平面的选取无关,D错。]
7 C [棋子起跳后只受重力作用,机械能守恒,A错;棋子在最高点具有水平方向的速度,所以离开平台时的动能大于mgh,落到平台上的速度要大于,B、D错;棋子从离开平台至运动到最高点过程中重力做功为WG=-mgh,所以重力势能增加mgh,C对。]
8 C [A、B的质量分别记为2m、m,当A落到地面上时,B恰好运动到与圆柱轴心等高处,以A、B整体为研究对象,则A、B组成的系统机械能守恒,故有2mgR-mgR=(2m+m)v2,A落到地面上以后,B以速度v竖直上抛,上升的高度为h′=,解得h′=R,此时绳子未绷直,故B上升的最大高度为R+h′=R,选项C正确。]
9 A [甲图中轻杆对小球不做功,小球的机械能守恒;乙图中A、B两球通过杆相互影响(例如开始时A球带动B球转动),轻杆对A的弹力不沿杆的方向,会对小球做功,所以每个小球的机械能不守恒,但把两个小球作为一个系统时系统的机械能守恒;丙图中细绳绷紧的过程虽然只有弹力作为内力做功,但弹力突变有内能转化,机械能不守恒;丁图中细绳会拉动小车运动,取地面为参考系,小球的运动轨迹不是圆弧,细绳会对小球做功,小球的机械能不守恒,把小球和小车当作一个系统,机械能才守恒。]
10 B [将A、B的速度分解为沿绳的方向和垂直于绳的方向,两滑块沿绳方向的速度相等,有vBcos 60°=vAcos 30°,所以vA=v,设A的质量为6m,B的质量为m;A、B组成的系统机械能守恒,有mgh=×6mv+mv2,所以有h=,绳长l=2h=,故B正确,A、C、D错误。]
11 D [B下滑时对A有压力,A对B有支持力。A向左滑动,水平方向发生位移,B对A做正功,A对B做负功。因而A、B各自的机械能不守恒,A、B、C错;A、B和地球组成的系统没有与外界发生机械能的转移,也没有摩擦,机械能没有转化为其他形式的能,系统的机械能守恒,D对。]
12 B [设物体动能等于势能时速度为v,根据机械能守恒mv2+Ep=mgh,又mv2=Ep,解得v=,而物体做自由落体运动,v=gt,解得t=,B正确。]
13 D [竖直上抛和沿斜面运动的物体,上升到最高点时,速度均为0,由机械能守恒得mgh=mv,所以h=,斜上抛运动物体在最高点速度不为零,设为v1,则mgh2=mv-mv,所以h2
15 C [物体到达海平面时位于参考平面以下,重力势能为-mgh,A错误;物体运动过程中,只有重力做功,机械能为mv,B、D错误;根据机械能守恒定律,可知物体在海平面上的动能Ek=mv2=mgh+mv,C正确。]
16[答案] (1)50 J (2)32 J
[解析] (1)木块压缩弹簧的过程中,木块和弹簧组成的系统机械能守恒,弹性势能最大时,对应木块的动能为零,故有
Epm=mv=×4×52 J=50 J。
(2)由机械能守恒有
mv=Ep1+mv
×4×52 J=Ep1+×4×32 J
得Ep1=32 J。
17 [答案] (1)20 J (2)20 m (3)10 m/s
[解析] (1)根据动能的表达式得Ek=mv=×0.1×202 J=20 J。
(2)根据机械能守恒定律mv=mgH,
解得H=20 m。
(3)根据机械能守恒定律,选抛出点为重力势能参考平面得mv=mv2+mgh,
解得v=10 m/s。
18[答案] 2 040 N
[解析] 运动员从开始滑下至c点,
由机械能守恒定律得mgH=mv2 ①
运动员滑至最低点时,由牛顿运动定律和向心力公式得N-mg=m ②
由①②得N=mg=2 040 N。
19[答案] (1)3 m/s (2)0.8 m (3)4.3 N
[解析] (1)小球沿圆弧形槽下滑到槽底端过程中机械能守恒,有
mgR=mv
解得v1=3 m/s。
(2)小球离开桌面后以3 m/s的初速度做平抛运动,竖直方向有
h=gt2,
小球恰好无碰撞地沿圆弧轨道切线从B点进入固定的竖直光滑圆弧轨道,则tan 53°=,
解得t=0.4 s,h=0.8 m。
(3)小球由A点到O点,由机械能守恒定律得
mg(h+r-rcos 53°)=mv-mv,
在O点,由牛顿第二定律得F-mg=m,
代入数据解得F=4.3 N,
根据牛顿第三定律,小球运动至O点时对圆弧轨道的压力大小为4.3 N。
20[答案]
[解析] 把A、B两小球和杆看成一个系统,杆对A、B两小球的弹力为系统的内力,对系统而言,只有重力做功,系统的机械能守恒。以A球在最低点的位置为零势能位置,则初状态:系统的动能为Ek1=0,重力势能为Ep1=2mgL,
末状态(即到竖直位置):
系统的动能为Ek2=mv+mv,
重力势能为Ep2=mg,
由机械能守恒定律得2mgL=mgL+mv+mv,
又因为在自由转动过程中A、B两球的角速度相同,则vA=2vB,
联立解得vA=,vB=。
21 [答案] (1) (2)3.5R
[解析] (1)物体在运动的全过程中只有重力做功,机械能守恒,选取B点为零势能点。设物体在B处的速度为vB,则mg·3R+mv=mv,
得v0=。
(2)设从B点上升到最高点的高度为HB,由机械能守恒可得mgHB=mv,HB=4.5R
所以离开C点后还能上升HC=HB-R=3.5R。
