8.2 重力势能 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案)
文档属性
| 名称 | 8.2 重力势能 同步练习-2021-2022学年高一下学期物理人教版(2019)必修第二册 (word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-11 08:14:27 | ||
图片预览


文档简介
第八章 机械能守恒定律
2.重力势能
1.某游客领着孩子游泰山时,孩子不小心将手中质量为m的皮球滑落,球从A点滚到了山脚下的B点,高度标记如图所示,则下列说法正确的是( )
A.从A到B的曲线轨迹长度不知道,无法求出此过程重力做的功
B.从A到B过程中阻力大小不知道,无法求出此过程重力做的功
C.从A到B重力做功mg(H+h)
D.从A到B重力做功mgH
2.关于重力势能的说法,正确的是( )
A.重力势能的大小只由重物本身决定
B.重力势能恒大于零或等于零
C.重力势能是物体和地球所共有的
D.在地面上的物体,它具有的重力势能一定等于零
3.西双湖风景区内的十七孔桥(如图甲)是除水晶塔之外的又一标志性建筑,它不仅是南北两湖的分界点,更是联系东西两方景区的交通要冲,其模型可简化为图乙。已知孔桥的拱高为h,A、B两点在同一水平面上。一游客在由A点运动到B点的过程中,以下说法正确的是( )
甲 乙
A.游客的重力势能先增大后减小,重力先做正功后做负功
B.游客的重力势能先减小后增大,重力先做负功后做正功
C.游客的重力势能先增大后减小,重力先做正功后做负功
D.游客在整个运动过程中重力做功为零
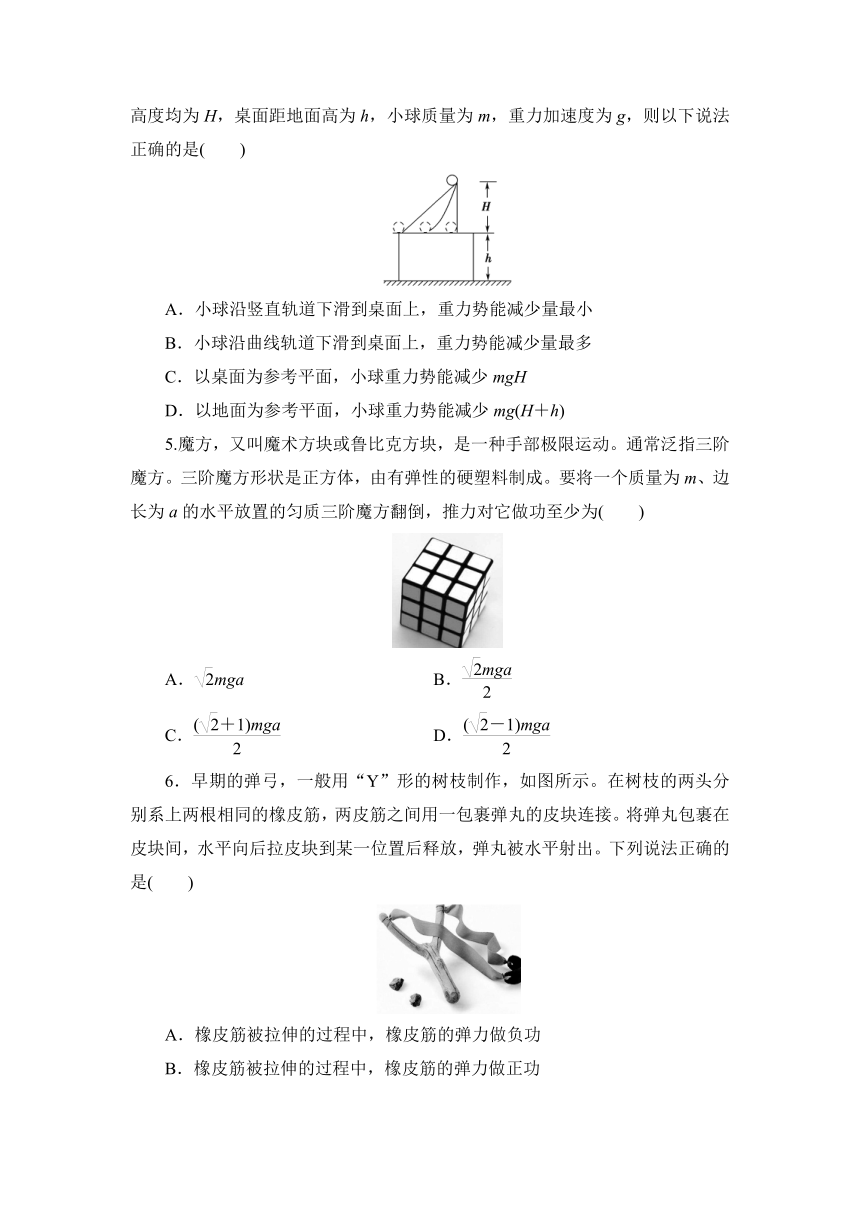
4.如图,静止的小球沿不同的光滑轨道由同一位置滑到水平桌面上,轨道高度均为H,桌面距地面高为h,小球质量为m,重力加速度为g,则以下说法正确的是( )
A.小球沿竖直轨道下滑到桌面上,重力势能减少量最小
B.小球沿曲线轨道下滑到桌面上,重力势能减少量最多
C.以桌面为参考平面,小球重力势能减少mgH
D.以地面为参考平面,小球重力势能减少mg(H+h)
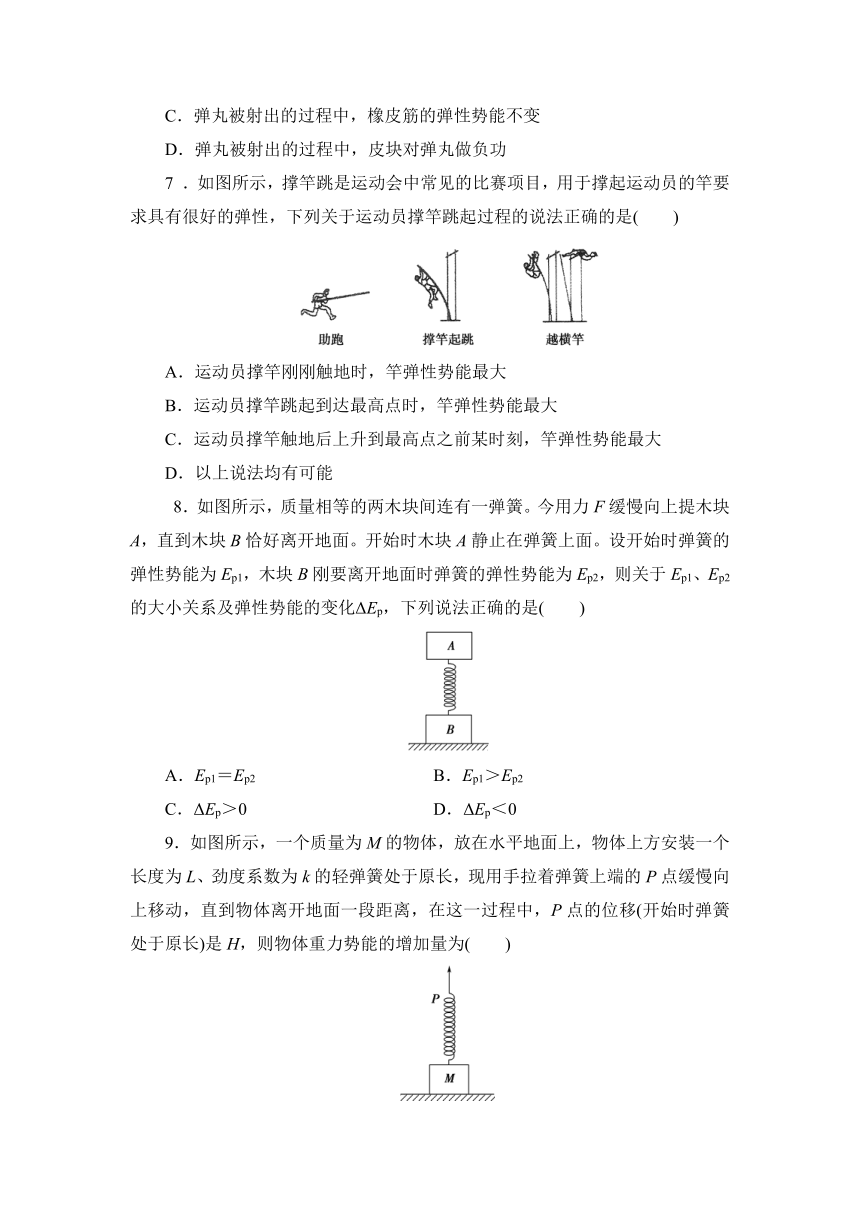
5.魔方,又叫魔术方块或鲁比克方块,是一种手部极限运动。通常泛指三阶魔方。三阶魔方形状是正方体,由有弹性的硬塑料制成。要将一个质量为m、边长为a的水平放置的匀质三阶魔方翻倒,推力对它做功至少为( )
A.mga B.
C. D.
6.早期的弹弓,一般用“Y”形的树枝制作,如图所示。在树枝的两头分别系上两根相同的橡皮筋,两皮筋之间用一包裹弹丸的皮块连接。将弹丸包裹在皮块间,水平向后拉皮块到某一位置后释放,弹丸被水平射出。下列说法正确的是( )
A.橡皮筋被拉伸的过程中,橡皮筋的弹力做负功
B.橡皮筋被拉伸的过程中,橡皮筋的弹力做正功
C.弹丸被射出的过程中,橡皮筋的弹性势能不变
D.弹丸被射出的过程中,皮块对弹丸做负功
7 .如图所示,撑竿跳是运动会中常见的比赛项目,用于撑起运动员的竿要求具有很好的弹性,下列关于运动员撑竿跳起过程的说法正确的是( )
A.运动员撑竿刚刚触地时,竿弹性势能最大
B.运动员撑竿跳起到达最高点时,竿弹性势能最大
C.运动员撑竿触地后上升到最高点之前某时刻,竿弹性势能最大
D.以上说法均有可能
8.如图所示,质量相等的两木块间连有一弹簧。今用力F缓慢向上提木块A,直到木块B恰好离开地面。开始时木块A静止在弹簧上面。设开始时弹簧的弹性势能为Ep1,木块B刚要离开地面时弹簧的弹性势能为Ep2,则关于Ep1、Ep2的大小关系及弹性势能的变化ΔEp,下列说法正确的是( )
A.Ep1=Ep2 B.Ep1>Ep2
C.ΔEp>0 D.ΔEp<0
9.如图所示,一个质量为M的物体,放在水平地面上,物体上方安装一个长度为L、劲度系数为k的轻弹簧处于原长,现用手拉着弹簧上端的P点缓慢向上移动,直到物体离开地面一段距离,在这一过程中,P点的位移(开始时弹簧处于原长)是H,则物体重力势能的增加量为( )
A.MgH B.MgH+
C.MgH- D.MgH-
10.物体从某高度处做自由落体运动,以地面为重力势能零点,下列所示图像中,能正确描述物体的重力势能与下落高度的关系的是( )
A B C D
11.下列关于重力势能的说法正确的是( )
A.重力势能是地球和物体共同具有的,而不是物体单独具有的
B.在同一高度,将物体以速度v0向不同方向抛出,落地时物体增加的重力势能一定相等
C.重力势能等于零的物体,重力不可能做功
D.在地面上的物体,它具有的重力势能一定等于零
A.只要发生形变,物体就具有弹性势能
B.某一弹簧的长度越长,其弹性势能就越大
C.在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关
D.弹簧的弹力做正功,其弹性势能增加
13.一个质量为100 g的球从1.8 m的高处落到一水平板上又弹回到1.25 m的高度,则整个过程中重力对球所做的功及球的重力势能的变化是(g取10 m/s2)( )
A.重力做了1.8 J的功
B.重力做了0.55 J的负功
C.球的重力势能一定减少了0.55 J
D.球的重力势能一定增加了1.25 J
14.如图所示,在光滑的水平面上有一小车,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下小车处于静止状态。当撤去力F后,小车向右运动,在小车向右运动的过程中,下列说法正确的是( )
A.弹簧的弹性势能逐渐减小
B.弹簧的弹性势能逐渐增大
C.弹簧的弹性势能先增大再减小
D.弹簧的弹性势能先减小再增大
15.在离地面80 m处无初速度地释放一小球,小球质量为m=200 g,不计空气阻力,g取10 m/s2,取释放点所在水平面为参考平面。求:
(1)在第2 s末小球的重力势能;
(2)在第3 s内重力所做的功和小球重力势能的变化量。
16.摩天轮是一种大型转轮状的机械建筑设施,上面挂在轮边缘的是供乘客搭的座舱。乘客坐在摩天轮座舱里,摩天轮慢慢地往上转,可以从高处俯瞰四周景色。我国目前最高的摩天轮——南昌之星的高度达到160 m。
问题:假设一个50 kg的乘客从地面乘坐该摩天轮到达最高点,g取10 m/s2,则:
(1)乘客重力做功为多少?
(2)乘客的重力势能变化了多少?
(3)由(1)、(2)可知,重力做功与重力势能的变化有什么关系?
17.起重机以的加速度将质量为m的物体沿竖直方向匀加速地提升高度h,则起重机钢索的拉力对物体做的功为多少?物体克服重力做的功为多少?物体的重力势能变化了多少?
18.在水平面上放一个竖直轻弹簧,弹簧上端与一个质量为m的木块相连,若在木块上再作用一个竖直向下的力F,使木块缓慢向下移动h,力F做功W1,此时木块再次处于平衡状态,如图所示。求:
(1)在木块下移h的过程中重力势能的减少量;
(2)在木块下移h的过程中弹性势能的增加量。
参考解析
1 D [重力做功与物体的运动路径无关,只与物体初、末位置的高度差有关。从A到B的高度差是H,故从A到B重力做的功是mgH,选项D正确。]
2 C [重力势能的表达式为Ep=mgh,与高度也有关,故A错误;高度具有相对性,重力势能也具有相对性;我们规定当物体位于参考平面下方时,重力势能为负值,故B错误;重力势能离不开重力,重力离不开地球,故重力势能是物体与地球系统所共有的,故C正确;重力势能的大小与零势能面的选取有关,并不一定以地面为参考平面,故地面上的物体重力势能不一定为零,故D错误。]
3 D [游客由A到桥顶,重力做负功,重力势能增加,由桥顶到B,重力做正功,重力势能减小,整个过程游客的重力势能先增大后减小,由于A、B等高,则整个过程中重力做功为零,重力势能变化量为零,故D正确,A、B、C错误。]
4 C [静止的小球沿不同的轨道由同一位置滑到水平桌面上,由于高度差相同,重力做功相同,所以重力势能减少量相同,故A、B错误;重力势能的变化量与零势能平面的选取无关,重力做功为mgH,则重力势能减少量为mgH,故C正确,D错误。]
5 D [推力对物体所做的功,增加了物体的重力势能,即WF=ΔEp,ΔEp=mg=mga,故D正确。]
6 A [在橡皮筋拉伸的过程中,橡皮筋的弹力与橡皮筋的位移方向相反,则橡皮筋的弹力做负功,故A正确,B错误;弹丸被射出的过程中,橡皮筋的形变量减小,则弹性势能减小,故C错误;弹丸被射出的过程中,皮块对弹丸的力与弹丸的位移方向相同,则皮块对弹丸做正功,故D错误。]
7 C [竿形变量最大时,弹性势能最大,竿刚触地时没有形变,人到最高点时,竿已由弯曲到基本完全伸直,故选项C正确。]
8 A [设开始时弹簧的形变量为x1,B刚要离开地面时弹簧的形变量为x2,则有kx1=mg,kx2=mg,可得x1=x2,所以Ep1=Ep2,ΔEp=0,选项A正确。]
9 C [物体离开地面时,弹簧伸长x=,重物上升的高度h=H-x,重力势能增加量Ep=Mgh=MgH-,故C正确。]
10 B [设物体开始下落时的重力势能为Ep0,物体下落高度h过程中重力势能减少量ΔEp=mgh,故物体下落高度h时的重力势能Ep=Ep0-ΔEp=Ep0-mgh,即Ep h图像为倾斜直线,B正确。]
11 A [重力势能是物体与地球共有的,A项正确;从同一高度下落,初末位置的高度差相同,重力势能的减少量相等,B错误;物体的重力势能是相对于参考平面而言的,D项错误;重力势能等于零的物体,可能落向更低处,重力可以做功,C项错误。]
12.关于弹性势能,下列说法正确的是( )
12 C [发生弹性形变的物体,恢复形变的过程能够对外做功,一定具有弹性势能,但发生完全非弹性形变的物体都不具有弹性势能,A错;在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关,与弹簧的长度无关,B错,C对;弹簧的弹力做正功,其弹性势能减少,D错。]
13 C [在整个过程中,球下降的高度为h=1.8 m-1.25 m=0.55 m,该过程中重力对球做的功为W=mgh=0.1×10×0.55 J=0.55 J,A、B错;重力做多少正功重力势能就减少多少,故球的重力势能一定减少了0.55 J,C对,D错。]
14 D [当撤去力F后,小车向右运动的过程中,弹簧先由压缩状态恢复到原长,然后再伸长,所以形变量先减小后增大,则弹簧的弹性势能先减小再增大。]
15[答案] (1)-40 J (2)50 J 小球的重力势能减少了50 J
[解析] (1)以释放点所在水平面为参考平面,在第2 s末小球所处的“高度”为
h=-gt2=-×10×22 m=-20 m
此时小球的重力势能Ep=mgh=200×10-3×10×(-20) J=-40 J。
(2)在第3 s末小球所处的“高度”为
h′=-gt′2=-×10×32 m=-45 m
第3 s内重力做的功为
W=mg(h-h′)=200×10-3×10×(-20+45) J=50 J
由重力做的功与重力势能变化量的关系可知,小球的重力势能减少了50 J。
16 [答案] (1)-80 000 J (2)增加80 000 J (3)大小相等
[解析] (1)乘客随摩天轮向上的位移大小为160 m,则重力做的功为
W=-mgh=-50×10×160 J=-80 000 J。
(2)乘客随摩天轮向上运动,重力势能增大;乘客的重力势能增加量为
ΔEp=mgh=50×10×160 J=80 000 J。
(3)由以上的计算可知,重力做功与重力势能的变化大小是相等的,重力做负功,重力势能增大。
17 [答案] mgh mgh 增加mgh
[解析] 由题意可知物体的加速度为a=,方向竖直向上,物体上升的高度为h。根据牛顿第二定律可得F-mg=ma,所以F=mg+ma=mg;故拉力做的功为WF=Fh=mgh。重力做的功为WG=-mgh,即物体克服重力做的功为mgh,物体的重力势能增加了mgh。
18 [答案] (1)mgh (2)W1+mgh
[解析] (1)根据重力做功与重力势能变化的关系有
ΔEp减=WG=mgh。
(2)根据弹力做功与弹性势能变化的关系有
ΔEp增=-W弹
又因木块缓慢下移,力F与重力mg的合力与弹力等大、反向,
所以W弹=-(W1+WG)=-(W1+mgh)
所以弹性势能增量ΔEp增=W1+mgh。
2.重力势能
1.某游客领着孩子游泰山时,孩子不小心将手中质量为m的皮球滑落,球从A点滚到了山脚下的B点,高度标记如图所示,则下列说法正确的是( )
A.从A到B的曲线轨迹长度不知道,无法求出此过程重力做的功
B.从A到B过程中阻力大小不知道,无法求出此过程重力做的功
C.从A到B重力做功mg(H+h)
D.从A到B重力做功mgH
2.关于重力势能的说法,正确的是( )
A.重力势能的大小只由重物本身决定
B.重力势能恒大于零或等于零
C.重力势能是物体和地球所共有的
D.在地面上的物体,它具有的重力势能一定等于零
3.西双湖风景区内的十七孔桥(如图甲)是除水晶塔之外的又一标志性建筑,它不仅是南北两湖的分界点,更是联系东西两方景区的交通要冲,其模型可简化为图乙。已知孔桥的拱高为h,A、B两点在同一水平面上。一游客在由A点运动到B点的过程中,以下说法正确的是( )
甲 乙
A.游客的重力势能先增大后减小,重力先做正功后做负功
B.游客的重力势能先减小后增大,重力先做负功后做正功
C.游客的重力势能先增大后减小,重力先做正功后做负功
D.游客在整个运动过程中重力做功为零
4.如图,静止的小球沿不同的光滑轨道由同一位置滑到水平桌面上,轨道高度均为H,桌面距地面高为h,小球质量为m,重力加速度为g,则以下说法正确的是( )
A.小球沿竖直轨道下滑到桌面上,重力势能减少量最小
B.小球沿曲线轨道下滑到桌面上,重力势能减少量最多
C.以桌面为参考平面,小球重力势能减少mgH
D.以地面为参考平面,小球重力势能减少mg(H+h)
5.魔方,又叫魔术方块或鲁比克方块,是一种手部极限运动。通常泛指三阶魔方。三阶魔方形状是正方体,由有弹性的硬塑料制成。要将一个质量为m、边长为a的水平放置的匀质三阶魔方翻倒,推力对它做功至少为( )
A.mga B.
C. D.
6.早期的弹弓,一般用“Y”形的树枝制作,如图所示。在树枝的两头分别系上两根相同的橡皮筋,两皮筋之间用一包裹弹丸的皮块连接。将弹丸包裹在皮块间,水平向后拉皮块到某一位置后释放,弹丸被水平射出。下列说法正确的是( )
A.橡皮筋被拉伸的过程中,橡皮筋的弹力做负功
B.橡皮筋被拉伸的过程中,橡皮筋的弹力做正功
C.弹丸被射出的过程中,橡皮筋的弹性势能不变
D.弹丸被射出的过程中,皮块对弹丸做负功
7 .如图所示,撑竿跳是运动会中常见的比赛项目,用于撑起运动员的竿要求具有很好的弹性,下列关于运动员撑竿跳起过程的说法正确的是( )
A.运动员撑竿刚刚触地时,竿弹性势能最大
B.运动员撑竿跳起到达最高点时,竿弹性势能最大
C.运动员撑竿触地后上升到最高点之前某时刻,竿弹性势能最大
D.以上说法均有可能
8.如图所示,质量相等的两木块间连有一弹簧。今用力F缓慢向上提木块A,直到木块B恰好离开地面。开始时木块A静止在弹簧上面。设开始时弹簧的弹性势能为Ep1,木块B刚要离开地面时弹簧的弹性势能为Ep2,则关于Ep1、Ep2的大小关系及弹性势能的变化ΔEp,下列说法正确的是( )
A.Ep1=Ep2 B.Ep1>Ep2
C.ΔEp>0 D.ΔEp<0
9.如图所示,一个质量为M的物体,放在水平地面上,物体上方安装一个长度为L、劲度系数为k的轻弹簧处于原长,现用手拉着弹簧上端的P点缓慢向上移动,直到物体离开地面一段距离,在这一过程中,P点的位移(开始时弹簧处于原长)是H,则物体重力势能的增加量为( )
A.MgH B.MgH+
C.MgH- D.MgH-
10.物体从某高度处做自由落体运动,以地面为重力势能零点,下列所示图像中,能正确描述物体的重力势能与下落高度的关系的是( )
A B C D
11.下列关于重力势能的说法正确的是( )
A.重力势能是地球和物体共同具有的,而不是物体单独具有的
B.在同一高度,将物体以速度v0向不同方向抛出,落地时物体增加的重力势能一定相等
C.重力势能等于零的物体,重力不可能做功
D.在地面上的物体,它具有的重力势能一定等于零
A.只要发生形变,物体就具有弹性势能
B.某一弹簧的长度越长,其弹性势能就越大
C.在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关
D.弹簧的弹力做正功,其弹性势能增加
13.一个质量为100 g的球从1.8 m的高处落到一水平板上又弹回到1.25 m的高度,则整个过程中重力对球所做的功及球的重力势能的变化是(g取10 m/s2)( )
A.重力做了1.8 J的功
B.重力做了0.55 J的负功
C.球的重力势能一定减少了0.55 J
D.球的重力势能一定增加了1.25 J
14.如图所示,在光滑的水平面上有一小车,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下小车处于静止状态。当撤去力F后,小车向右运动,在小车向右运动的过程中,下列说法正确的是( )
A.弹簧的弹性势能逐渐减小
B.弹簧的弹性势能逐渐增大
C.弹簧的弹性势能先增大再减小
D.弹簧的弹性势能先减小再增大
15.在离地面80 m处无初速度地释放一小球,小球质量为m=200 g,不计空气阻力,g取10 m/s2,取释放点所在水平面为参考平面。求:
(1)在第2 s末小球的重力势能;
(2)在第3 s内重力所做的功和小球重力势能的变化量。
16.摩天轮是一种大型转轮状的机械建筑设施,上面挂在轮边缘的是供乘客搭的座舱。乘客坐在摩天轮座舱里,摩天轮慢慢地往上转,可以从高处俯瞰四周景色。我国目前最高的摩天轮——南昌之星的高度达到160 m。
问题:假设一个50 kg的乘客从地面乘坐该摩天轮到达最高点,g取10 m/s2,则:
(1)乘客重力做功为多少?
(2)乘客的重力势能变化了多少?
(3)由(1)、(2)可知,重力做功与重力势能的变化有什么关系?
17.起重机以的加速度将质量为m的物体沿竖直方向匀加速地提升高度h,则起重机钢索的拉力对物体做的功为多少?物体克服重力做的功为多少?物体的重力势能变化了多少?
18.在水平面上放一个竖直轻弹簧,弹簧上端与一个质量为m的木块相连,若在木块上再作用一个竖直向下的力F,使木块缓慢向下移动h,力F做功W1,此时木块再次处于平衡状态,如图所示。求:
(1)在木块下移h的过程中重力势能的减少量;
(2)在木块下移h的过程中弹性势能的增加量。
参考解析
1 D [重力做功与物体的运动路径无关,只与物体初、末位置的高度差有关。从A到B的高度差是H,故从A到B重力做的功是mgH,选项D正确。]
2 C [重力势能的表达式为Ep=mgh,与高度也有关,故A错误;高度具有相对性,重力势能也具有相对性;我们规定当物体位于参考平面下方时,重力势能为负值,故B错误;重力势能离不开重力,重力离不开地球,故重力势能是物体与地球系统所共有的,故C正确;重力势能的大小与零势能面的选取有关,并不一定以地面为参考平面,故地面上的物体重力势能不一定为零,故D错误。]
3 D [游客由A到桥顶,重力做负功,重力势能增加,由桥顶到B,重力做正功,重力势能减小,整个过程游客的重力势能先增大后减小,由于A、B等高,则整个过程中重力做功为零,重力势能变化量为零,故D正确,A、B、C错误。]
4 C [静止的小球沿不同的轨道由同一位置滑到水平桌面上,由于高度差相同,重力做功相同,所以重力势能减少量相同,故A、B错误;重力势能的变化量与零势能平面的选取无关,重力做功为mgH,则重力势能减少量为mgH,故C正确,D错误。]
5 D [推力对物体所做的功,增加了物体的重力势能,即WF=ΔEp,ΔEp=mg=mga,故D正确。]
6 A [在橡皮筋拉伸的过程中,橡皮筋的弹力与橡皮筋的位移方向相反,则橡皮筋的弹力做负功,故A正确,B错误;弹丸被射出的过程中,橡皮筋的形变量减小,则弹性势能减小,故C错误;弹丸被射出的过程中,皮块对弹丸的力与弹丸的位移方向相同,则皮块对弹丸做正功,故D错误。]
7 C [竿形变量最大时,弹性势能最大,竿刚触地时没有形变,人到最高点时,竿已由弯曲到基本完全伸直,故选项C正确。]
8 A [设开始时弹簧的形变量为x1,B刚要离开地面时弹簧的形变量为x2,则有kx1=mg,kx2=mg,可得x1=x2,所以Ep1=Ep2,ΔEp=0,选项A正确。]
9 C [物体离开地面时,弹簧伸长x=,重物上升的高度h=H-x,重力势能增加量Ep=Mgh=MgH-,故C正确。]
10 B [设物体开始下落时的重力势能为Ep0,物体下落高度h过程中重力势能减少量ΔEp=mgh,故物体下落高度h时的重力势能Ep=Ep0-ΔEp=Ep0-mgh,即Ep h图像为倾斜直线,B正确。]
11 A [重力势能是物体与地球共有的,A项正确;从同一高度下落,初末位置的高度差相同,重力势能的减少量相等,B错误;物体的重力势能是相对于参考平面而言的,D项错误;重力势能等于零的物体,可能落向更低处,重力可以做功,C项错误。]
12.关于弹性势能,下列说法正确的是( )
12 C [发生弹性形变的物体,恢复形变的过程能够对外做功,一定具有弹性势能,但发生完全非弹性形变的物体都不具有弹性势能,A错;在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关,与弹簧的长度无关,B错,C对;弹簧的弹力做正功,其弹性势能减少,D错。]
13 C [在整个过程中,球下降的高度为h=1.8 m-1.25 m=0.55 m,该过程中重力对球做的功为W=mgh=0.1×10×0.55 J=0.55 J,A、B错;重力做多少正功重力势能就减少多少,故球的重力势能一定减少了0.55 J,C对,D错。]
14 D [当撤去力F后,小车向右运动的过程中,弹簧先由压缩状态恢复到原长,然后再伸长,所以形变量先减小后增大,则弹簧的弹性势能先减小再增大。]
15[答案] (1)-40 J (2)50 J 小球的重力势能减少了50 J
[解析] (1)以释放点所在水平面为参考平面,在第2 s末小球所处的“高度”为
h=-gt2=-×10×22 m=-20 m
此时小球的重力势能Ep=mgh=200×10-3×10×(-20) J=-40 J。
(2)在第3 s末小球所处的“高度”为
h′=-gt′2=-×10×32 m=-45 m
第3 s内重力做的功为
W=mg(h-h′)=200×10-3×10×(-20+45) J=50 J
由重力做的功与重力势能变化量的关系可知,小球的重力势能减少了50 J。
16 [答案] (1)-80 000 J (2)增加80 000 J (3)大小相等
[解析] (1)乘客随摩天轮向上的位移大小为160 m,则重力做的功为
W=-mgh=-50×10×160 J=-80 000 J。
(2)乘客随摩天轮向上运动,重力势能增大;乘客的重力势能增加量为
ΔEp=mgh=50×10×160 J=80 000 J。
(3)由以上的计算可知,重力做功与重力势能的变化大小是相等的,重力做负功,重力势能增大。
17 [答案] mgh mgh 增加mgh
[解析] 由题意可知物体的加速度为a=,方向竖直向上,物体上升的高度为h。根据牛顿第二定律可得F-mg=ma,所以F=mg+ma=mg;故拉力做的功为WF=Fh=mgh。重力做的功为WG=-mgh,即物体克服重力做的功为mgh,物体的重力势能增加了mgh。
18 [答案] (1)mgh (2)W1+mgh
[解析] (1)根据重力做功与重力势能变化的关系有
ΔEp减=WG=mgh。
(2)根据弹力做功与弹性势能变化的关系有
ΔEp增=-W弹
又因木块缓慢下移,力F与重力mg的合力与弹力等大、反向,
所以W弹=-(W1+WG)=-(W1+mgh)
所以弹性势能增量ΔEp增=W1+mgh。
