第一章 空间向量与立体几何单元测试-2021-2022学年高二上学期数学人教A版(2019))选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 第一章 空间向量与立体几何单元测试-2021-2022学年高二上学期数学人教A版(2019))选择性必修第一册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 12:47:14 | ||
图片预览


文档简介
第一章 空间向量与立体几何
一、单选题
1.,,若,则实数的值是( )
A. B. C.2 D.0
2.如图,在正四面体P ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论不成立的是( )
A.BC∥平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面PAE D.平面PDE⊥平面ABC
3.已知正方体的棱长为2,点,分别是棱,的中点,点在平面内,点在线段上,若,则长度的最小值为( )
A. B. C. D.
4.如图,三棱锥S﹣ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,CA的中点,记直线SE与SF所成的角为α,直线SG与平面SAB所成的角为β,平面SEG与平面SBC所成的锐二面角为γ,则( )
A.α>γ>β B.α>β>γ C.γ>α>β D.γ>β>α
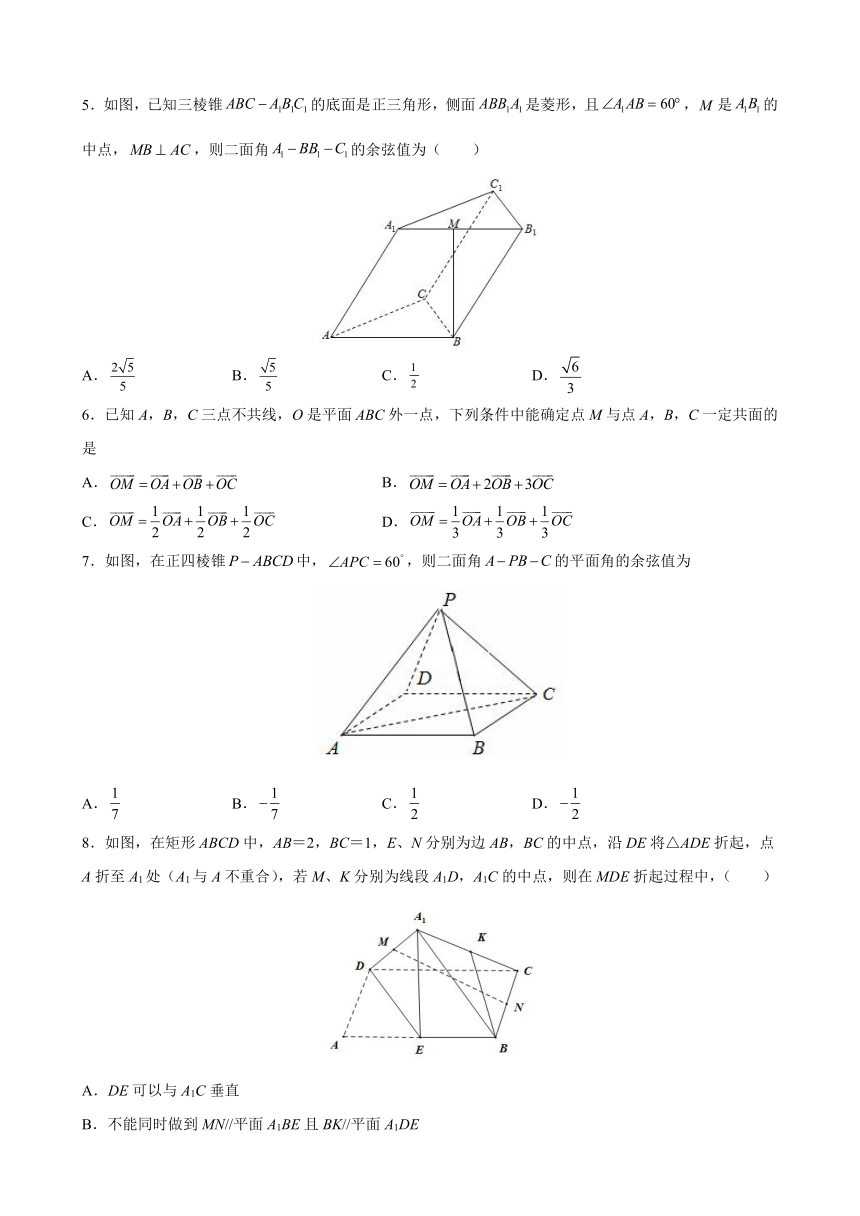
5.如图,已知三棱锥的底面是正三角形,侧面是菱形,且,是的中点,,则二面角的余弦值为( )
A. B. C. D.
6.已知A,B,C三点不共线,O是平面ABC外一点,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
C. D.
7.如图,在正四棱锥中,,则二面角的平面角的余弦值为
A. B. C. D.
8.如图,在矩形ABCD中,AB=2,BC=1,E、N分别为边AB,BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为线段A1D,A1C的中点,则在MDE折起过程中,( )
A.DE可以与A1C垂直
B.不能同时做到MN//平面A1BE且BK//平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.直线A1C、BK与平面BCDE所成角分别为θ1、θ2,θ1,θ2能够同时取得最大值
二、多选题
9.空间四个点,,,,,,为空间的一个基底,则下列说法正确的是( )
A.,,,四点不共线
B.,,,四点共面,但不共线
C.,,,四点中任意三点不共线
D.,,,四点不共面
10.如图所示,在正三棱柱ABC﹣A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF.则AF的长度为( )
A.a B. C.2a D.
11.已知ABCD﹣A1B1C1D1为正方体,下列说法中正确的是( )
A.
B.
C.向量与向量的夹角是60°
D.正方体ABCD﹣A1B1C1D1的体积为
12.(多选题)正三棱柱中,,则( )
A.与底面的成角的正弦值为
B.与底面的成角的正弦值为
C.与侧面的成角的正弦值为
D.与侧面的成角的正弦值为
三、填空题
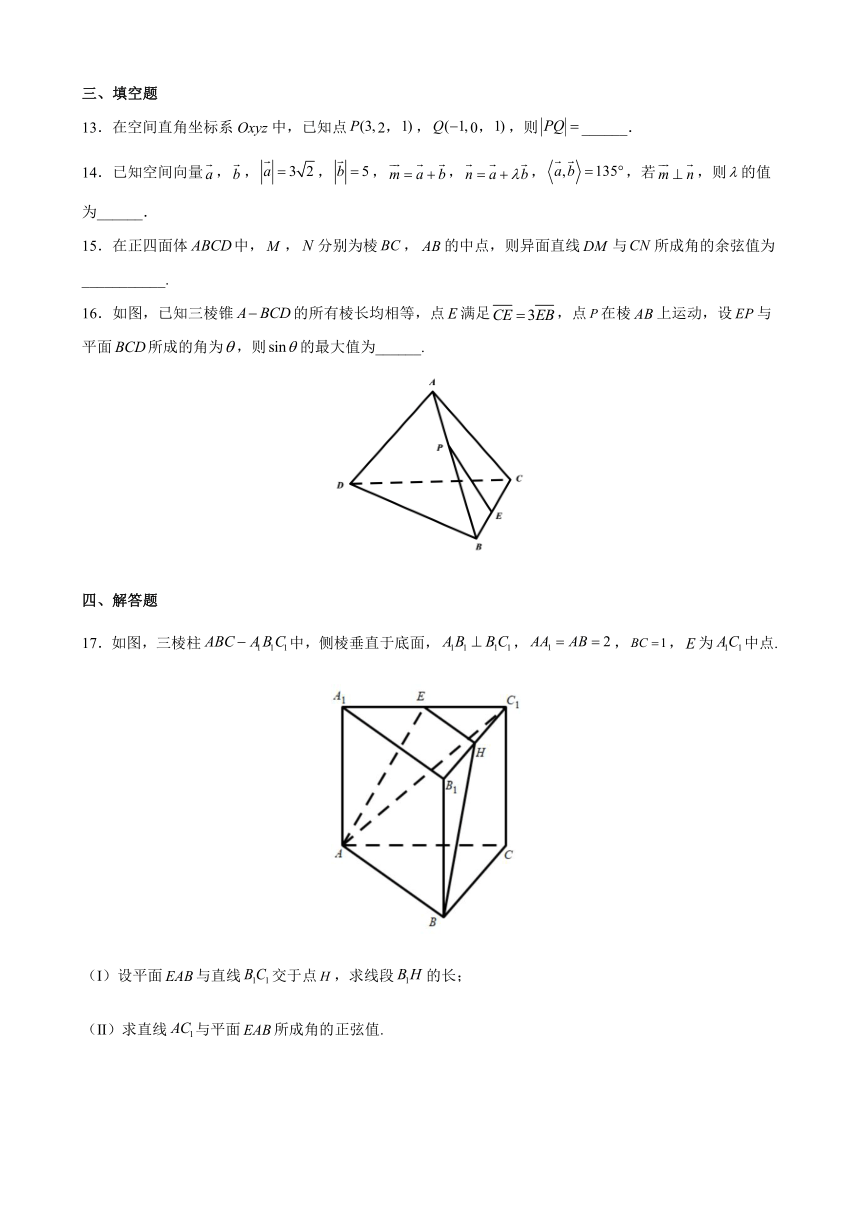
13.在空间直角坐标系Oxyz中,已知点2,,0,,则______.
14.已知空间向量,,,,,,,若,则的值为______.
15.在正四面体中,,分别为棱,的中点,则异面直线与所成角的余弦值为___________.
16.如图,已知三棱锥的所有棱长均相等,点满足,点在棱上运动,设与平面所成的角为,则的最大值为______.
四、解答题
17.如图,三棱柱中,侧棱垂直于底面,,,,为中点.
(Ⅰ)设平面与直线交于点,求线段的长;
(Ⅱ)求直线与平面所成角的正弦值.
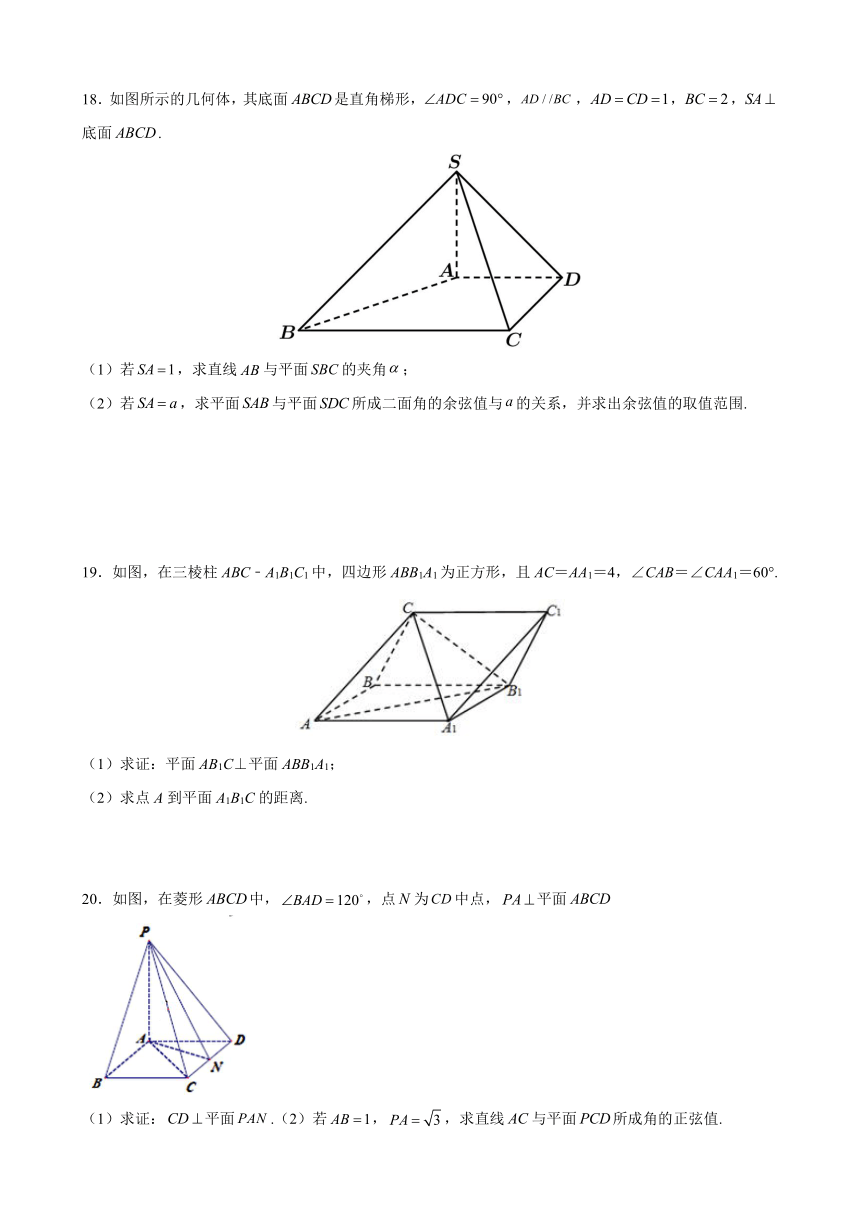
18.如图所示的几何体,其底面是直角梯形,,,,,底面.
(1)若,求直线与平面的夹角;
(2)若,求平面与平面所成二面角的余弦值与的关系,并求出余弦值的取值范围.
19.如图,在三棱柱ABC﹣A1B1C1中,四边形ABB1A1为正方形,且AC=AA1=4,∠CAB=∠CAA1=60°.
(1)求证:平面AB1C⊥平面ABB1A1;
(2)求点A到平面A1B1C的距离.
20.如图,在菱形中,,点为中点,平面
(1)求证:平面.(2)若,,求直线与平面所成角的正弦值.
21.在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.
(1)若P是DF的中点,求异面直线BE与CP所成角的余弦值;
(2)若二面角D﹣AP﹣C的正弦值为,求PF的长度.
22.如图,菱形与正所在平面互相垂直,平面,,.
(1)证明:平面;
(2)若,求直线与平面所成角的正弦值.
参考答案
1.D
【解析】因为,且,
根据空间向量平行的坐标表示公式可得:,
解得:,,
故选:D
2.D
【解析】因为BC∥DF,DF 平面PDF,BC 平面PDF,
所以BC∥平面PDF,故选项A正确;
在正四面体中,AE⊥BC,PE⊥BC,AE∩PE=E,
且AE,PE 平面PAE,
所以BC⊥平面PAE,
因为DF∥BC,所以DF⊥平面PAE,
又DF 平面PDF,
从而平面PDF⊥平面PAE.
因此选项B,C均正确.
故选:D
3.C
【解析】如图,设中点为,因为为的中点,
所以平面,即,
因为,所以,
所以点在以为圆心,半径为1的位于平面上的半圆上,
作平面图如图所示,
由图像知,的最小值即到的距离减去半径,
,
,所以,
所以的最小值:.
故选:C
4.A
【解析】因为AB⊥BC,SA=SB=SC,所以AB⊥SE,所以AB⊥平面SGE,AB⊥SG,
又SG⊥AC,所以SG⊥平面ABC,
过G作SE的垂线l,显然l垂直平面SAB,
故直线SG与平面SAB所成的角为β=∠GSE,
同理,平面SEG与平面SBC所成的锐二面角为γ=∠FSG,
由tanγ=,得γ>β,γ也是直线SF与平面SEG所成的角,
由cosα=cosβ cosγ<cosγ,则α>γ,所以α>γ>β,
故选:A.
5.B
【解析】解:取的中点,连接,,则,
又侧面是菱形,且,
所以,
又,所以四边形为平行四边形,所以,
又,所以,平面
建立以为坐标原点,的反向延长线,,分别为,,轴的空间直角坐标系,如图:
设,则,
则平面的法向量为,
,,,,,
则,,
设平面的法向量为,
则,令,得,
,
∴二面角的余弦值是.
故选:B.
6.D
【解析】不妨设.
对于A选项,,由于的竖坐标,故不在平面上,故A选项错误.
对于B选项,,由于的竖坐标,故不在平面上,故B选项错误.
对于C选项,,由于的竖坐标,故不在平面上,故C选项错误.
对于D选项,,由于的竖坐标为,故在平面上,也即四点共面.下面证明结论一定成立:
由,得,
即,故存在,使得成立,也即四点共面.
故选:D.
7.B
【解析】由于几何体为正四棱锥,故,在内分别作边上的高.故是二面角所成二面角的平面角.设,则,由于,故,则.由得,则在三角形中,.故选B.
8.D
【解析】对于A,连接EC,如图,
假设DE⊥A1C,由平面几何的知识可得DE⊥EC,
∴DE⊥平面A1EC,∴DE⊥A1E,而A1ED=45°,故假设不成立,∴A错误;
对于B,取DE,DC中点G,F,连接GM,GN,FK,FB,如图,
∴GM//A1E,GN//EB,FK//A1D,BF//DE,
∴平面A1BE//平面GMN,平面FKB//平面A1DE,
故能同时做到MN//平面A1BE且BK//平面A1DE,∴B错误;
对于C,连接ME,EN,DN,如图,
当MN⊥A1D时,,
而,∴MN与ME不垂直,即MN不垂直平面A1DE,∴C错误;
对于D,∵A1在以DE为直径球面上,球心为G,且A1G⊥DE,
∴A1的轨迹为圆弧(A1与A不重合,在平面下方时与该情况一致),如图弧AF所示,
∴当点A1到平面BCDE的距离最大时,直线A1C与平面BCDE所成角取得最大值;
连接EC,取EC中点T,连接TK,TB,如图,
∴,,
又,,∴,
∴,为定值,
∴当点K到平面BCDE的距离最大时,直线BK与平面BCDE所成角取得最大值,
此时点A1到平面BCDE的距离也最大,∴D正确.
故选:D.
9.ACD
【解析】因为,,为空间的一个基底,
所以,,不共面,
即,,,四点中任意三点不共线,且四点不共面,
故选:ACD
10.AC
【解析】解:平面,.
在矩形中,设.
①
,②.
联立①②解得,或.
则的长度为或.
故选:AC.
11.AB
【解析】由向量的加法得到:,∵,∴,所以A正确;
∵,AB1⊥A1C,∴,故B正确;
∵△ACD1是等边三角形,∴∠AD1C=60°,又A1B∥D1C,∴异面直线AD1与A1B所成的夹角为60°,但是向量与向量的夹角是120°,故C不正确;
∵AB⊥AA1,∴,故=0,因此D不正确.
故选:AB.
12.BC
【解析】如图,取中点,中点,并连接,则,,三条直线两两垂直,
则分别以这三条直线为轴,轴,轴建立如图所示空间直角坐标系;
设,则.
.
.底面的其中一个法向量为,
与底面的成角的正弦值为,错对.
的中点的坐标为,
∴侧面的其中一个法向量为,
与侧面的成角的正弦值为:,
故对错;
故选:BC.
13.
【解析】在空间直角坐标系Oxyz中,
点2,,0,,
.
故答案为.
14.
【解析】由题意,知.
由,得,
即,解得.
故答案为:.
15.
【解析】解:为棱的中点,设
又 为棱的中点
又的两两夹角都为,并设
又
异面直线与所成角的余弦值为
故答案为:
16.
【解析】依题意可知,该几何体为正四面体,设顶点在底面的射影是,是底面中心,连接,过作,交于,连接.
设正四面体的棱长为,.在三角形中,由余弦定理得.由于平面,所以平面,,所以是直线与平面所成的角,设为.在三角形中,,所以.所以.所以当时,的最大值为.
故答案为:
17.(Ⅰ);(Ⅱ).
【解析】(Ⅰ)由棱柱特点知:平面平面,
平面,平面,
平面平面,平面,,
又为中点,为中点,;
(Ⅱ)以为坐标原点,为轴,可建立如图所示的空间直角坐标系,
则,,,,
,,,
设平面的法向量,
,令,解得:,,,
,
即直线与平面所成角的正弦值为.
18.(1);(2)平面与平面所成二面角的平面角的余弦值为,余弦值的范围是.
【解析】(1)在直角梯形中,作交BC于H,因,则,又底面,以为原点,建立如图所示的空间直角坐标系,
因此,,,,,,
则,,,
设平面的法向量为,则,即,令得,
于是得,
所以;
(2),,设平面的法向量为,则,即,令得,
,,设平面的法向量为,,即,令得,
,
因此,平面与平面所成二面角的平面角的余弦值为,
因,
所以平面与平面所成二面角的平面角的余弦值为,其范围是.
19.(1)证明见解析;(2) .
【解析】解:(1)证明:连接A1B,设AB1∩A1B=O,连接CO,
∵AC=AC,∠CAB=∠CAA1,AB=AA1,∴CAB≌CAA1,∴CB=CA1,
∵O为A1B的中点,∴A1B⊥CO,∵四边形ABB1A1为正方形,∴A1B⊥AB1,
又平面AB1C,CO∩AB1=O,∴A1B⊥平面AB1C,
∵平面ABB1A1,∴平面AB1C⊥平面ABB1A1,
(2)解:∵CA=AA1=4,∠CAA1=60°,∴CA1=4,
在RtCOA1中,又,∴,又,AC=4,
∴OA2+OC2=AC2,∴CO⊥AO,
∵平面AB1C⊥平面ABB1A1,平面AB1C∩平面ABB1A1=AB1,∴CO⊥平面ABB1A1,
∴CO为三棱锥C﹣AA1B1的高,∴,
∵CA1=A1B1=B1C=4,∴,
∴点A到平面A1B1C的距离.
20.(1)见解析(2)
【解析】(1)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.
∵PA⊥平面ABCD,CD 平面ABCD,∴CD⊥PA.PA∩AN=A,∴CD⊥平面PAN.
(2)由(1)知,CD⊥平面PAN,CD 平面PCD,∴平面PAN⊥平面PCD,且平面PAN∩平面PCD=PN,
过A作AH⊥PN于H,则AH⊥平面PCD,连接CH,则∠ACH为直线AC与平面PCD所成角.
在RT△PAN中,PA,AN,由勾股定理得出PN,根据面积相等法得AH.
在RT△ACH中,sin∠ACH.即直线AC与平面PCD所成角的正弦值是.
21.(1).(2).
【解析】(1)∵BAF=90°,∴AF⊥AB,
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,
∴AF⊥平面ABCD,又四边形ABCD为矩形,
∴以A为原点,AB为x轴,AD为y轴,AF为z轴,建立空间直角坐标系,
∵AD=2,AB=AF=2EF=2,P是DF的中点,
∴B(2,0,0),E(1,0,2),C(2,2,0),P(0,1,1),
(﹣1,0,2),(﹣2,﹣1,1),
设异面直线BE与CP所成角的平面角为θ,
则cosθ,
∴异面直线BE与CP所成角的余弦值为.
(2)A(0,0,0),C(2,2,0),F(0,0,2),D(0,2,0),
设P(a,b,c),,0≤λ≤1,即(a,b,c﹣2)=λ(0,2,﹣2),
解得a=0,b=2λ,c=2﹣2λ,∴P(0,2λ,2﹣2λ),
(0,2λ,2﹣2λ),(2,2,0),
设平面APC的法向量(x,y,z),
则,取x=1,得(1,﹣1,),
平面ADP的法向量(1,0,0),
∵二面角D﹣AP﹣C的正弦值为,
∴|cos|,
解得,∴P(0,,),
∴PF的长度|PF|.
22.(1)证明过程详见解析(2)
【解析】解:(1)如图,过点作于,连接EH,∴.
∵平面平面,平面,
平面平面于 ∴ 平面.
又∵平面,.∴,
∴四边形为平行四边形. ∴,
∵平面,平面,
∴平面.
(2)连接.由(1)得为中点,又,为等边三角形,
∴.分别以,,为轴建立
如图所示的空间直角坐标系.
则,,,.
,, ,
设平面的法向量为.
由,得
令,得.
,
直线与平面所成角的正弦值为.
一、单选题
1.,,若,则实数的值是( )
A. B. C.2 D.0
2.如图,在正四面体P ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论不成立的是( )
A.BC∥平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面PAE D.平面PDE⊥平面ABC
3.已知正方体的棱长为2,点,分别是棱,的中点,点在平面内,点在线段上,若,则长度的最小值为( )
A. B. C. D.
4.如图,三棱锥S﹣ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,CA的中点,记直线SE与SF所成的角为α,直线SG与平面SAB所成的角为β,平面SEG与平面SBC所成的锐二面角为γ,则( )
A.α>γ>β B.α>β>γ C.γ>α>β D.γ>β>α
5.如图,已知三棱锥的底面是正三角形,侧面是菱形,且,是的中点,,则二面角的余弦值为( )
A. B. C. D.
6.已知A,B,C三点不共线,O是平面ABC外一点,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
C. D.
7.如图,在正四棱锥中,,则二面角的平面角的余弦值为
A. B. C. D.
8.如图,在矩形ABCD中,AB=2,BC=1,E、N分别为边AB,BC的中点,沿DE将△ADE折起,点A折至A1处(A1与A不重合),若M、K分别为线段A1D,A1C的中点,则在MDE折起过程中,( )
A.DE可以与A1C垂直
B.不能同时做到MN//平面A1BE且BK//平面A1DE
C.当MN⊥A1D时,MN⊥平面A1DE
D.直线A1C、BK与平面BCDE所成角分别为θ1、θ2,θ1,θ2能够同时取得最大值
二、多选题
9.空间四个点,,,,,,为空间的一个基底,则下列说法正确的是( )
A.,,,四点不共线
B.,,,四点共面,但不共线
C.,,,四点中任意三点不共线
D.,,,四点不共面
10.如图所示,在正三棱柱ABC﹣A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF.则AF的长度为( )
A.a B. C.2a D.
11.已知ABCD﹣A1B1C1D1为正方体,下列说法中正确的是( )
A.
B.
C.向量与向量的夹角是60°
D.正方体ABCD﹣A1B1C1D1的体积为
12.(多选题)正三棱柱中,,则( )
A.与底面的成角的正弦值为
B.与底面的成角的正弦值为
C.与侧面的成角的正弦值为
D.与侧面的成角的正弦值为
三、填空题
13.在空间直角坐标系Oxyz中,已知点2,,0,,则______.
14.已知空间向量,,,,,,,若,则的值为______.
15.在正四面体中,,分别为棱,的中点,则异面直线与所成角的余弦值为___________.
16.如图,已知三棱锥的所有棱长均相等,点满足,点在棱上运动,设与平面所成的角为,则的最大值为______.
四、解答题
17.如图,三棱柱中,侧棱垂直于底面,,,,为中点.
(Ⅰ)设平面与直线交于点,求线段的长;
(Ⅱ)求直线与平面所成角的正弦值.
18.如图所示的几何体,其底面是直角梯形,,,,,底面.
(1)若,求直线与平面的夹角;
(2)若,求平面与平面所成二面角的余弦值与的关系,并求出余弦值的取值范围.
19.如图,在三棱柱ABC﹣A1B1C1中,四边形ABB1A1为正方形,且AC=AA1=4,∠CAB=∠CAA1=60°.
(1)求证:平面AB1C⊥平面ABB1A1;
(2)求点A到平面A1B1C的距离.
20.如图,在菱形中,,点为中点,平面
(1)求证:平面.(2)若,,求直线与平面所成角的正弦值.
21.在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.
(1)若P是DF的中点,求异面直线BE与CP所成角的余弦值;
(2)若二面角D﹣AP﹣C的正弦值为,求PF的长度.
22.如图,菱形与正所在平面互相垂直,平面,,.
(1)证明:平面;
(2)若,求直线与平面所成角的正弦值.
参考答案
1.D
【解析】因为,且,
根据空间向量平行的坐标表示公式可得:,
解得:,,
故选:D
2.D
【解析】因为BC∥DF,DF 平面PDF,BC 平面PDF,
所以BC∥平面PDF,故选项A正确;
在正四面体中,AE⊥BC,PE⊥BC,AE∩PE=E,
且AE,PE 平面PAE,
所以BC⊥平面PAE,
因为DF∥BC,所以DF⊥平面PAE,
又DF 平面PDF,
从而平面PDF⊥平面PAE.
因此选项B,C均正确.
故选:D
3.C
【解析】如图,设中点为,因为为的中点,
所以平面,即,
因为,所以,
所以点在以为圆心,半径为1的位于平面上的半圆上,
作平面图如图所示,
由图像知,的最小值即到的距离减去半径,
,
,所以,
所以的最小值:.
故选:C
4.A
【解析】因为AB⊥BC,SA=SB=SC,所以AB⊥SE,所以AB⊥平面SGE,AB⊥SG,
又SG⊥AC,所以SG⊥平面ABC,
过G作SE的垂线l,显然l垂直平面SAB,
故直线SG与平面SAB所成的角为β=∠GSE,
同理,平面SEG与平面SBC所成的锐二面角为γ=∠FSG,
由tanγ=,得γ>β,γ也是直线SF与平面SEG所成的角,
由cosα=cosβ cosγ<cosγ,则α>γ,所以α>γ>β,
故选:A.
5.B
【解析】解:取的中点,连接,,则,
又侧面是菱形,且,
所以,
又,所以四边形为平行四边形,所以,
又,所以,平面
建立以为坐标原点,的反向延长线,,分别为,,轴的空间直角坐标系,如图:
设,则,
则平面的法向量为,
,,,,,
则,,
设平面的法向量为,
则,令,得,
,
∴二面角的余弦值是.
故选:B.
6.D
【解析】不妨设.
对于A选项,,由于的竖坐标,故不在平面上,故A选项错误.
对于B选项,,由于的竖坐标,故不在平面上,故B选项错误.
对于C选项,,由于的竖坐标,故不在平面上,故C选项错误.
对于D选项,,由于的竖坐标为,故在平面上,也即四点共面.下面证明结论一定成立:
由,得,
即,故存在,使得成立,也即四点共面.
故选:D.
7.B
【解析】由于几何体为正四棱锥,故,在内分别作边上的高.故是二面角所成二面角的平面角.设,则,由于,故,则.由得,则在三角形中,.故选B.
8.D
【解析】对于A,连接EC,如图,
假设DE⊥A1C,由平面几何的知识可得DE⊥EC,
∴DE⊥平面A1EC,∴DE⊥A1E,而A1ED=45°,故假设不成立,∴A错误;
对于B,取DE,DC中点G,F,连接GM,GN,FK,FB,如图,
∴GM//A1E,GN//EB,FK//A1D,BF//DE,
∴平面A1BE//平面GMN,平面FKB//平面A1DE,
故能同时做到MN//平面A1BE且BK//平面A1DE,∴B错误;
对于C,连接ME,EN,DN,如图,
当MN⊥A1D时,,
而,∴MN与ME不垂直,即MN不垂直平面A1DE,∴C错误;
对于D,∵A1在以DE为直径球面上,球心为G,且A1G⊥DE,
∴A1的轨迹为圆弧(A1与A不重合,在平面下方时与该情况一致),如图弧AF所示,
∴当点A1到平面BCDE的距离最大时,直线A1C与平面BCDE所成角取得最大值;
连接EC,取EC中点T,连接TK,TB,如图,
∴,,
又,,∴,
∴,为定值,
∴当点K到平面BCDE的距离最大时,直线BK与平面BCDE所成角取得最大值,
此时点A1到平面BCDE的距离也最大,∴D正确.
故选:D.
9.ACD
【解析】因为,,为空间的一个基底,
所以,,不共面,
即,,,四点中任意三点不共线,且四点不共面,
故选:ACD
10.AC
【解析】解:平面,.
在矩形中,设.
①
,②.
联立①②解得,或.
则的长度为或.
故选:AC.
11.AB
【解析】由向量的加法得到:,∵,∴,所以A正确;
∵,AB1⊥A1C,∴,故B正确;
∵△ACD1是等边三角形,∴∠AD1C=60°,又A1B∥D1C,∴异面直线AD1与A1B所成的夹角为60°,但是向量与向量的夹角是120°,故C不正确;
∵AB⊥AA1,∴,故=0,因此D不正确.
故选:AB.
12.BC
【解析】如图,取中点,中点,并连接,则,,三条直线两两垂直,
则分别以这三条直线为轴,轴,轴建立如图所示空间直角坐标系;
设,则.
.
.底面的其中一个法向量为,
与底面的成角的正弦值为,错对.
的中点的坐标为,
∴侧面的其中一个法向量为,
与侧面的成角的正弦值为:,
故对错;
故选:BC.
13.
【解析】在空间直角坐标系Oxyz中,
点2,,0,,
.
故答案为.
14.
【解析】由题意,知.
由,得,
即,解得.
故答案为:.
15.
【解析】解:为棱的中点,设
又 为棱的中点
又的两两夹角都为,并设
又
异面直线与所成角的余弦值为
故答案为:
16.
【解析】依题意可知,该几何体为正四面体,设顶点在底面的射影是,是底面中心,连接,过作,交于,连接.
设正四面体的棱长为,.在三角形中,由余弦定理得.由于平面,所以平面,,所以是直线与平面所成的角,设为.在三角形中,,所以.所以.所以当时,的最大值为.
故答案为:
17.(Ⅰ);(Ⅱ).
【解析】(Ⅰ)由棱柱特点知:平面平面,
平面,平面,
平面平面,平面,,
又为中点,为中点,;
(Ⅱ)以为坐标原点,为轴,可建立如图所示的空间直角坐标系,
则,,,,
,,,
设平面的法向量,
,令,解得:,,,
,
即直线与平面所成角的正弦值为.
18.(1);(2)平面与平面所成二面角的平面角的余弦值为,余弦值的范围是.
【解析】(1)在直角梯形中,作交BC于H,因,则,又底面,以为原点,建立如图所示的空间直角坐标系,
因此,,,,,,
则,,,
设平面的法向量为,则,即,令得,
于是得,
所以;
(2),,设平面的法向量为,则,即,令得,
,,设平面的法向量为,,即,令得,
,
因此,平面与平面所成二面角的平面角的余弦值为,
因,
所以平面与平面所成二面角的平面角的余弦值为,其范围是.
19.(1)证明见解析;(2) .
【解析】解:(1)证明:连接A1B,设AB1∩A1B=O,连接CO,
∵AC=AC,∠CAB=∠CAA1,AB=AA1,∴CAB≌CAA1,∴CB=CA1,
∵O为A1B的中点,∴A1B⊥CO,∵四边形ABB1A1为正方形,∴A1B⊥AB1,
又平面AB1C,CO∩AB1=O,∴A1B⊥平面AB1C,
∵平面ABB1A1,∴平面AB1C⊥平面ABB1A1,
(2)解:∵CA=AA1=4,∠CAA1=60°,∴CA1=4,
在RtCOA1中,又,∴,又,AC=4,
∴OA2+OC2=AC2,∴CO⊥AO,
∵平面AB1C⊥平面ABB1A1,平面AB1C∩平面ABB1A1=AB1,∴CO⊥平面ABB1A1,
∴CO为三棱锥C﹣AA1B1的高,∴,
∵CA1=A1B1=B1C=4,∴,
∴点A到平面A1B1C的距离.
20.(1)见解析(2)
【解析】(1)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.
∵PA⊥平面ABCD,CD 平面ABCD,∴CD⊥PA.PA∩AN=A,∴CD⊥平面PAN.
(2)由(1)知,CD⊥平面PAN,CD 平面PCD,∴平面PAN⊥平面PCD,且平面PAN∩平面PCD=PN,
过A作AH⊥PN于H,则AH⊥平面PCD,连接CH,则∠ACH为直线AC与平面PCD所成角.
在RT△PAN中,PA,AN,由勾股定理得出PN,根据面积相等法得AH.
在RT△ACH中,sin∠ACH.即直线AC与平面PCD所成角的正弦值是.
21.(1).(2).
【解析】(1)∵BAF=90°,∴AF⊥AB,
又∵平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,
∴AF⊥平面ABCD,又四边形ABCD为矩形,
∴以A为原点,AB为x轴,AD为y轴,AF为z轴,建立空间直角坐标系,
∵AD=2,AB=AF=2EF=2,P是DF的中点,
∴B(2,0,0),E(1,0,2),C(2,2,0),P(0,1,1),
(﹣1,0,2),(﹣2,﹣1,1),
设异面直线BE与CP所成角的平面角为θ,
则cosθ,
∴异面直线BE与CP所成角的余弦值为.
(2)A(0,0,0),C(2,2,0),F(0,0,2),D(0,2,0),
设P(a,b,c),,0≤λ≤1,即(a,b,c﹣2)=λ(0,2,﹣2),
解得a=0,b=2λ,c=2﹣2λ,∴P(0,2λ,2﹣2λ),
(0,2λ,2﹣2λ),(2,2,0),
设平面APC的法向量(x,y,z),
则,取x=1,得(1,﹣1,),
平面ADP的法向量(1,0,0),
∵二面角D﹣AP﹣C的正弦值为,
∴|cos|,
解得,∴P(0,,),
∴PF的长度|PF|.
22.(1)证明过程详见解析(2)
【解析】解:(1)如图,过点作于,连接EH,∴.
∵平面平面,平面,
平面平面于 ∴ 平面.
又∵平面,.∴,
∴四边形为平行四边形. ∴,
∵平面,平面,
∴平面.
(2)连接.由(1)得为中点,又,为等边三角形,
∴.分别以,,为轴建立
如图所示的空间直角坐标系.
则,,,.
,, ,
设平面的法向量为.
由,得
令,得.
,
直线与平面所成角的正弦值为.
