《第3章概率的进一步认识》同步练习 2021-2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 《第3章概率的进一步认识》同步练习 2021-2022学年北师大版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 12:01:02 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册《第3章概率的进一步认识》同步练习(附答案)
一.选择题
1.在“石头、剪子、布”的游戏中,当你出“剪刀”时,对手与你打平的概率为( )
A. B. C. D.
2.把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )
A. B. C. D.
3.下列表述中,正确的是( )
A.“任意一个五边形的外角和是540°”是必然事件
B.抛掷一枚质地均匀的硬币100次,正面朝上的次数正好为50次
C.抛掷两枚质地均匀的银币,正好一枚正面朝上,一枚反面朝上的概率为
D.“367人中至少有两人的生日相同”是随机事件
4.在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L2发光的概率是( )
A. B. C. D.
5.小明和小斌参加学校社团活动,准备在舞蹈社,文学社和漫画社里选择一项,那么两人同时选择漫画社的概率为( )
A. B. C. D.
6.学校组织学生外出集体劳动时,为九年级学生安排了三辆车.九年级的小明与小亮都可以从这三辆车中任选一辆搭乘,则他俩搭乘同一辆车的概率为( )
A. B. C. D.
7.同一枚硬币小明先抛一次,然后小亮再抛一次,两次都是反面朝上的概率是( )
A. B. C. D.
8.某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )
A. B. C. D.
9.在一个不透明的盒子中装有若干个黑球和白球,这些球除颜色外其余均相同,将球搅匀后任意摸出一个球,记下颜色后放回,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,则摸到白球的概率约为( )
A.0.8 B.0.3 C.0.2 D.0.5
10.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球试验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
11.一个不透明的袋子中装有除颜色外均相同的4个白球和若干个绿球,每次摇均匀后随机摸出一个球,记下颜色后再放回袋中,经大量试验,发现摸到绿球的频率稳定在0.2,则摸到绿球的概率约为( )
A.0.2 B.0.5 C.0.6 D.0.8
12.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个,若随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为( )
A.3 B.4 C.5 D.6
13.下列说法错误的是( )
A.通过大量重复试验,可以用频率估计概率 B.概率很小的事件不可能发生
C.必然事件发生的概率是1 D.投一枚图钉,“钉尖朝上”的概率不能用列举法计算
14.在一个不透明的口袋中装有3个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
二.填空题
15.如图,一个可以自由转动的圆形转盘被互相垂直的一条半径和直径分成了3个分别标有数字的扇形区域,转动转盘,待转盘自动停止后指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时称为转动转盘一次(若指针指向两个扇形的边界线,则不计为转动次数,重新转动转盘,直到指针指向扇形内部为止).
(1)转动转盘一次,转出的数字是﹣1的概率为 .
(2)转动转盘两次,用画树状图或列表法求这两次分别转出的数字之积为负数的概率.
16.某校围棋队共有4名队员,分别是:小明、小红、小聪、小丽,其中小明、小红来自八年级,小聪小丽来自九年级,现准备抽取两名队员参加集训.
(1)若从八年级、九年级中各随机抽取一人,则小红和小丽恰好被抽到参加集训的概率为 ;
(2)若从四名队员中随机抽取两名队员,请用列表法或画树状图法求抽到小明和小聪的概率.
三.解答题
17.我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如表(单位:颗):
182 195 201 179 208 204 186 192 210 204
175 193 200 203 188 197 212 207 185 206
188 186 198 202 221 199 219 208 187 224
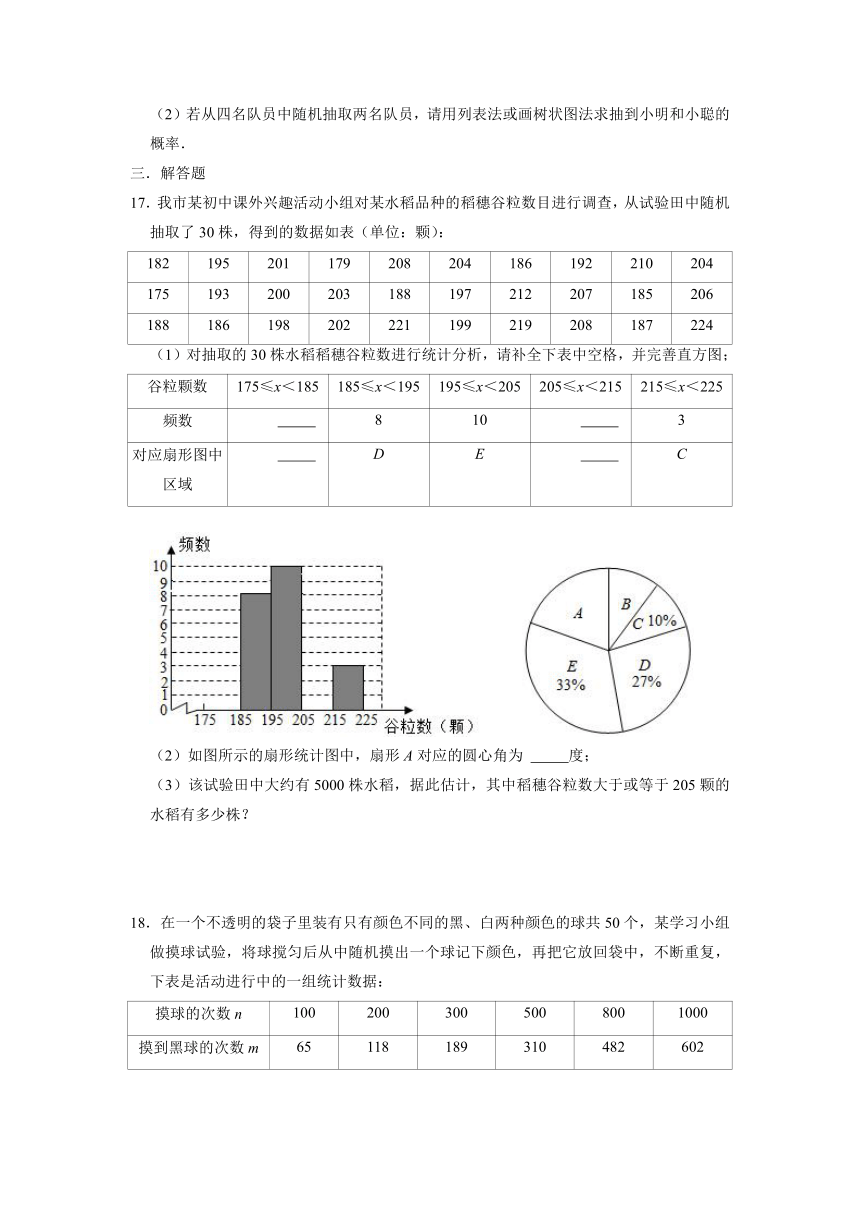
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图;
谷粒颗数 175≤x<185 185≤x<195 195≤x<205 205≤x<215 215≤x<225
频数 8 10 3
对应扇形图中区域 D E C
(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度;
(3)该试验田中大约有5000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
18.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000
摸到黑球的次数m 65 118 189 310 482 602
摸到黑球的频率 0.65 0.59 0.63 0.62 0.603 0.602
(1)请估计:当n很大时,摸到黑球的频率将会接近 (精确到0.1);
(2)试估计袋子中有黑球 个;
(3)若学习小组通过实验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 个或减少黑球 个.
19.下面三个实验中我们都可以通过看图估算或者通过图形计算各自概率:
(1)在一次实验中,老师共做了400次掷图钉游戏并记录了游戏的结果,绘制了钉尖朝上的频率折线统计图,如(1)图,请估计钉尖朝上的概率;
(2)如(2)图是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,计算指针落在蓝色区域的概率;
(3)有一个小球在如(3)图的地板上自由滚动,地板上的每个格子都是边长为1的正方形,求小球最终停留在黑色区域的概率.
20.下表是该校服生产厂对一批夏装校服质量检测的情况:
抽取校服数(套) 200 500 1000 1500 2000 3000
合格品数(套) 188 471 946 1426 1898 2850
合格品频率(精确到0.001) 0.940 0.942 0.946 0.951 a b
(1)a= ,b= ;
(2)从这批校服中任意抽取一套是合格品的概率估计值是 ;(精确到0.01)
(3)若要生产380000套合格的夏装校服,该厂估计要生产多少套夏装校服?
参考答案
1.解:画树状图为:
共有3种可能的结果数,其中对手与你打平的结果数为1,
所以对手与你打平的概率=,
故选:B.
2.解:画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和大于3的结果有6种,
∴两次摸出的小球标号的和大于3的概率是=,
故选:D.
3.解:A.“任意一个五边形的外角和是540°”是不可能事件,所以A选项不符合题意;
B.抛掷一枚质地均匀的硬币100次,正面朝上为随机事件,正面向上的次数可能为50次,所以B选项不符合题意;
C.抛掷两枚质地均匀的银币,,共有4种等可能的结果数,其中正好一枚正面朝上,一枚反面朝上的结果数为2,则正好一枚正面朝上,一枚反面朝上的概率==,所以C选项符合题意;
D.“367人中至少有两人的生日相同”是必然事件,所以D选项不符合题意.
故选:C.
4.解:画树状图为:
共有6种等可能的结果,其中能让灯泡L2发光的结果数为2,
所以能让灯泡L2发光的概率==.
故选:A.
5.解:列表如下:
舞蹈 文学 漫画
舞蹈 (舞蹈,舞蹈) (文学,舞蹈) (漫画,舞蹈)
文学 (舞蹈,文学) (文学,文学) (漫画,文学)
漫画 (舞蹈,漫画) (文学,漫画) (漫画,漫画)
由表格知,共有9种等可能结果,其中两人同时选择漫画社的只有1种结果,
所以两人同时选择漫画社的概率为,
故选:C.
6.解:设三辆车记为A、B、C,
树状图如下图所示:
由上可得,一共有9种可能性,其中他俩搭乘同一辆车的可能性有3种,
∴他俩搭乘同一辆车的概率是,
故选:A.
7.解:根据题意画图如下:
共有4种等可能的情况数,其中两次都是反面朝上的有1种,
则两次都是反面朝上的概率是.
故选:B.
8.解:把“垃圾分类”“文明出行”“低碳环保”三个宣传队分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,小华和小丽恰好选到同一个宣传队的结果有3种,
∴小华和小丽恰好选到同一个宣传队的概率为=,
故选:C.
9.解:因为通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,
所以摸到白球的概率约为0.2,
故选:C.
10.解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
11.解:大量重复试验中,事件发生的频率可以估计概率,
∵经大量试验,发现摸到绿球的频率稳定在0.2,
∴摸到绿球的概率约为0.2,
故选:A.
12.解:根据题意,得:=0.4,
解得n=3,
经检验:n=3是分式方程的解且符合题意,
故选:A.
13.解:A.通过大量重复试验,可以用频率估计概率,此说法正确,不符合题意;
B.概率很小的事件发生的可能性小,但不表示不可能发生,此说法错误,符合题意;
C.必然事件发生的概率是1,此说法正确,不符合题意;
D.投一枚图钉,由于图形的构造不均匀,“钉尖朝上”的概率不能用列举法计算,此说法正确,不符合题意;
故选:B.
14.解:设袋中白球的个数为x,
根据题意,得:=20%,
解得x=12,
经检验x=12是分式方程的解,
所以口袋中白球可能有12个,
故选:D.
15.解:(1)∵标有数字“﹣1”的扇形的圆心角为90°,
∴转出的数字是﹣1的概率是=.
故答案为:;
(2)将标有数字2的扇形两等分,树状图如下:
一共有16种等可能结果,其中两次分别转出的数字之和为负数的有6种,
则两次分别转出的数字之积为负数的概率是=.
16.解:(1)列表如下:
小明 小红
小聪 (小明,小聪) (小红,小聪)
小丽 (小明,小丽) (小红,小丽)
由表可知,共有4种等可能结果,其中小红和小丽恰好被抽到参加集训的有1种结果,
所以小红和小丽恰好被抽到参加集训的概率为,
故答案为:;
(2)列表如下:
小明 小红 小聪 小丽
小明 (小红,小明) (小聪,小明) (小丽,小明)
小红 (小明,小红) (小聪,小红) (小丽,小红)
小聪 (小明,小聪) (小红,小聪) (小丽,小聪)
小丽 (小明,小丽) (小红,小丽) (小聪,小丽)
由表知,共有12种等可能结果,其中抽到小明和小聪的有2种结果,
∴抽到小明和小聪的概率为=.
17.解:(1)填表如下:
谷粒颗数 175≤x<185 185≤x<195 195≤x<205 205≤x<215 215≤x<225
频数 3 8 10 6 3
对应扇形图中区域 B D E A C
如图所示:
(2)扇形A对应的圆心角为:360°×=72度;
故答案为:72.
(3)(株).
即据此估计,其中稻穗谷粒数大于或等于205颗的水稻有1500株.
18.解:(1)观察表格得:当n很大时,摸到黑球的频率将会接近0.6,
故答案为:0.6;
(2)黑球的个数为50×0.6=30个,
故答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以使得黑球和白球的个数相同,
即:在袋子中增加相同的白球10个或减少黑球10个,
故答案为:10,10.
19.解:(1)如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率为0.4.
(2)如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率为.
(3)如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率为=.
20.解:(1)1898÷2000=0.949,2850÷3000=0.950,
故答案为:0.949,0.950;
(2)由图可知,随着取样的不断增大,任意抽取一套是合格品的频率在0.95附近波动,
故答案为:0.95;
(3)根据(2)的合格频率估计为:380000÷0.95=400000(套),
答:该厂估计要生产400000套夏装校服.
一.选择题
1.在“石头、剪子、布”的游戏中,当你出“剪刀”时,对手与你打平的概率为( )
A. B. C. D.
2.把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )
A. B. C. D.
3.下列表述中,正确的是( )
A.“任意一个五边形的外角和是540°”是必然事件
B.抛掷一枚质地均匀的硬币100次,正面朝上的次数正好为50次
C.抛掷两枚质地均匀的银币,正好一枚正面朝上,一枚反面朝上的概率为
D.“367人中至少有两人的生日相同”是随机事件
4.在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L2发光的概率是( )
A. B. C. D.
5.小明和小斌参加学校社团活动,准备在舞蹈社,文学社和漫画社里选择一项,那么两人同时选择漫画社的概率为( )
A. B. C. D.
6.学校组织学生外出集体劳动时,为九年级学生安排了三辆车.九年级的小明与小亮都可以从这三辆车中任选一辆搭乘,则他俩搭乘同一辆车的概率为( )
A. B. C. D.
7.同一枚硬币小明先抛一次,然后小亮再抛一次,两次都是反面朝上的概率是( )
A. B. C. D.
8.某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )
A. B. C. D.
9.在一个不透明的盒子中装有若干个黑球和白球,这些球除颜色外其余均相同,将球搅匀后任意摸出一个球,记下颜色后放回,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,则摸到白球的概率约为( )
A.0.8 B.0.3 C.0.2 D.0.5
10.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球试验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
11.一个不透明的袋子中装有除颜色外均相同的4个白球和若干个绿球,每次摇均匀后随机摸出一个球,记下颜色后再放回袋中,经大量试验,发现摸到绿球的频率稳定在0.2,则摸到绿球的概率约为( )
A.0.2 B.0.5 C.0.6 D.0.8
12.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个,若随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为( )
A.3 B.4 C.5 D.6
13.下列说法错误的是( )
A.通过大量重复试验,可以用频率估计概率 B.概率很小的事件不可能发生
C.必然事件发生的概率是1 D.投一枚图钉,“钉尖朝上”的概率不能用列举法计算
14.在一个不透明的口袋中装有3个红球和若干个白球,他们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在20%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
二.填空题
15.如图,一个可以自由转动的圆形转盘被互相垂直的一条半径和直径分成了3个分别标有数字的扇形区域,转动转盘,待转盘自动停止后指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时称为转动转盘一次(若指针指向两个扇形的边界线,则不计为转动次数,重新转动转盘,直到指针指向扇形内部为止).
(1)转动转盘一次,转出的数字是﹣1的概率为 .
(2)转动转盘两次,用画树状图或列表法求这两次分别转出的数字之积为负数的概率.
16.某校围棋队共有4名队员,分别是:小明、小红、小聪、小丽,其中小明、小红来自八年级,小聪小丽来自九年级,现准备抽取两名队员参加集训.
(1)若从八年级、九年级中各随机抽取一人,则小红和小丽恰好被抽到参加集训的概率为 ;
(2)若从四名队员中随机抽取两名队员,请用列表法或画树状图法求抽到小明和小聪的概率.
三.解答题
17.我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如表(单位:颗):
182 195 201 179 208 204 186 192 210 204
175 193 200 203 188 197 212 207 185 206
188 186 198 202 221 199 219 208 187 224
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图;
谷粒颗数 175≤x<185 185≤x<195 195≤x<205 205≤x<215 215≤x<225
频数 8 10 3
对应扇形图中区域 D E C
(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度;
(3)该试验田中大约有5000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
18.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000
摸到黑球的次数m 65 118 189 310 482 602
摸到黑球的频率 0.65 0.59 0.63 0.62 0.603 0.602
(1)请估计:当n很大时,摸到黑球的频率将会接近 (精确到0.1);
(2)试估计袋子中有黑球 个;
(3)若学习小组通过实验结果,想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以在袋子中增加相同的白球 个或减少黑球 个.
19.下面三个实验中我们都可以通过看图估算或者通过图形计算各自概率:
(1)在一次实验中,老师共做了400次掷图钉游戏并记录了游戏的结果,绘制了钉尖朝上的频率折线统计图,如(1)图,请估计钉尖朝上的概率;
(2)如(2)图是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,计算指针落在蓝色区域的概率;
(3)有一个小球在如(3)图的地板上自由滚动,地板上的每个格子都是边长为1的正方形,求小球最终停留在黑色区域的概率.
20.下表是该校服生产厂对一批夏装校服质量检测的情况:
抽取校服数(套) 200 500 1000 1500 2000 3000
合格品数(套) 188 471 946 1426 1898 2850
合格品频率(精确到0.001) 0.940 0.942 0.946 0.951 a b
(1)a= ,b= ;
(2)从这批校服中任意抽取一套是合格品的概率估计值是 ;(精确到0.01)
(3)若要生产380000套合格的夏装校服,该厂估计要生产多少套夏装校服?
参考答案
1.解:画树状图为:
共有3种可能的结果数,其中对手与你打平的结果数为1,
所以对手与你打平的概率=,
故选:B.
2.解:画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和大于3的结果有6种,
∴两次摸出的小球标号的和大于3的概率是=,
故选:D.
3.解:A.“任意一个五边形的外角和是540°”是不可能事件,所以A选项不符合题意;
B.抛掷一枚质地均匀的硬币100次,正面朝上为随机事件,正面向上的次数可能为50次,所以B选项不符合题意;
C.抛掷两枚质地均匀的银币,,共有4种等可能的结果数,其中正好一枚正面朝上,一枚反面朝上的结果数为2,则正好一枚正面朝上,一枚反面朝上的概率==,所以C选项符合题意;
D.“367人中至少有两人的生日相同”是必然事件,所以D选项不符合题意.
故选:C.
4.解:画树状图为:
共有6种等可能的结果,其中能让灯泡L2发光的结果数为2,
所以能让灯泡L2发光的概率==.
故选:A.
5.解:列表如下:
舞蹈 文学 漫画
舞蹈 (舞蹈,舞蹈) (文学,舞蹈) (漫画,舞蹈)
文学 (舞蹈,文学) (文学,文学) (漫画,文学)
漫画 (舞蹈,漫画) (文学,漫画) (漫画,漫画)
由表格知,共有9种等可能结果,其中两人同时选择漫画社的只有1种结果,
所以两人同时选择漫画社的概率为,
故选:C.
6.解:设三辆车记为A、B、C,
树状图如下图所示:
由上可得,一共有9种可能性,其中他俩搭乘同一辆车的可能性有3种,
∴他俩搭乘同一辆车的概率是,
故选:A.
7.解:根据题意画图如下:
共有4种等可能的情况数,其中两次都是反面朝上的有1种,
则两次都是反面朝上的概率是.
故选:B.
8.解:把“垃圾分类”“文明出行”“低碳环保”三个宣传队分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,小华和小丽恰好选到同一个宣传队的结果有3种,
∴小华和小丽恰好选到同一个宣传队的概率为=,
故选:C.
9.解:因为通过大量重复摸球试验后,发现摸到白球的频率稳定在0.2,
所以摸到白球的概率约为0.2,
故选:C.
10.解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
11.解:大量重复试验中,事件发生的频率可以估计概率,
∵经大量试验,发现摸到绿球的频率稳定在0.2,
∴摸到绿球的概率约为0.2,
故选:A.
12.解:根据题意,得:=0.4,
解得n=3,
经检验:n=3是分式方程的解且符合题意,
故选:A.
13.解:A.通过大量重复试验,可以用频率估计概率,此说法正确,不符合题意;
B.概率很小的事件发生的可能性小,但不表示不可能发生,此说法错误,符合题意;
C.必然事件发生的概率是1,此说法正确,不符合题意;
D.投一枚图钉,由于图形的构造不均匀,“钉尖朝上”的概率不能用列举法计算,此说法正确,不符合题意;
故选:B.
14.解:设袋中白球的个数为x,
根据题意,得:=20%,
解得x=12,
经检验x=12是分式方程的解,
所以口袋中白球可能有12个,
故选:D.
15.解:(1)∵标有数字“﹣1”的扇形的圆心角为90°,
∴转出的数字是﹣1的概率是=.
故答案为:;
(2)将标有数字2的扇形两等分,树状图如下:
一共有16种等可能结果,其中两次分别转出的数字之和为负数的有6种,
则两次分别转出的数字之积为负数的概率是=.
16.解:(1)列表如下:
小明 小红
小聪 (小明,小聪) (小红,小聪)
小丽 (小明,小丽) (小红,小丽)
由表可知,共有4种等可能结果,其中小红和小丽恰好被抽到参加集训的有1种结果,
所以小红和小丽恰好被抽到参加集训的概率为,
故答案为:;
(2)列表如下:
小明 小红 小聪 小丽
小明 (小红,小明) (小聪,小明) (小丽,小明)
小红 (小明,小红) (小聪,小红) (小丽,小红)
小聪 (小明,小聪) (小红,小聪) (小丽,小聪)
小丽 (小明,小丽) (小红,小丽) (小聪,小丽)
由表知,共有12种等可能结果,其中抽到小明和小聪的有2种结果,
∴抽到小明和小聪的概率为=.
17.解:(1)填表如下:
谷粒颗数 175≤x<185 185≤x<195 195≤x<205 205≤x<215 215≤x<225
频数 3 8 10 6 3
对应扇形图中区域 B D E A C
如图所示:
(2)扇形A对应的圆心角为:360°×=72度;
故答案为:72.
(3)(株).
即据此估计,其中稻穗谷粒数大于或等于205颗的水稻有1500株.
18.解:(1)观察表格得:当n很大时,摸到黑球的频率将会接近0.6,
故答案为:0.6;
(2)黑球的个数为50×0.6=30个,
故答案为:30;
(3)想使得在这个不透明袋子中每次摸到黑球的可能性大小为50%,则可以使得黑球和白球的个数相同,
即:在袋子中增加相同的白球10个或减少黑球10个,
故答案为:10,10.
19.解:(1)如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率为0.4.
(2)如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率为.
(3)如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率为=.
20.解:(1)1898÷2000=0.949,2850÷3000=0.950,
故答案为:0.949,0.950;
(2)由图可知,随着取样的不断增大,任意抽取一套是合格品的频率在0.95附近波动,
故答案为:0.95;
(3)根据(2)的合格频率估计为:380000÷0.95=400000(套),
答:该厂估计要生产400000套夏装校服.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
