13.2 用坐标表示 轴对称-初中数学人教版八年级上册同步试题精编(word版 含答案)
文档属性
| 名称 | 13.2 用坐标表示 轴对称-初中数学人教版八年级上册同步试题精编(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 16:48:20 | ||
图片预览




文档简介
13.2.2用坐标表示轴对称
一、选择题
1.蝴蝶标本可以近似地看作轴对称图形,如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(﹣5,3),则其关于y轴对称的点B的坐标为( )
A.(5,3) B.(5,﹣3) C.(﹣5,﹣3) D.(3,5)
2.已知点与点关于某条直线对称,则这条直线是( )
A.轴 B.轴
C.过点且垂直于轴的直线 D.过点且平行于轴的直线
3.已知平面直角坐标系中点A的坐标为,则下列结论正确的是( )
A.点A到x轴的距离为5
B.点A到y轴的距离为6
C.点A关于x轴对称的点的坐标为
D.点A关于y轴对称的点的坐标为
4.若点与点关于轴对称,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
5.已知点A(m-l,-2)与点B(2,n+1)关于x轴对称,则m=______,n=______。
三、解答题
6.如图,在平面直角坐标系中,点,,.
(1)在图中画出关于y轴对称的,并直接写出点和点的坐标;(不写画法,保留画图痕迹)
(2)在x轴上画出点P,使得的值最小.
(3)求的面积
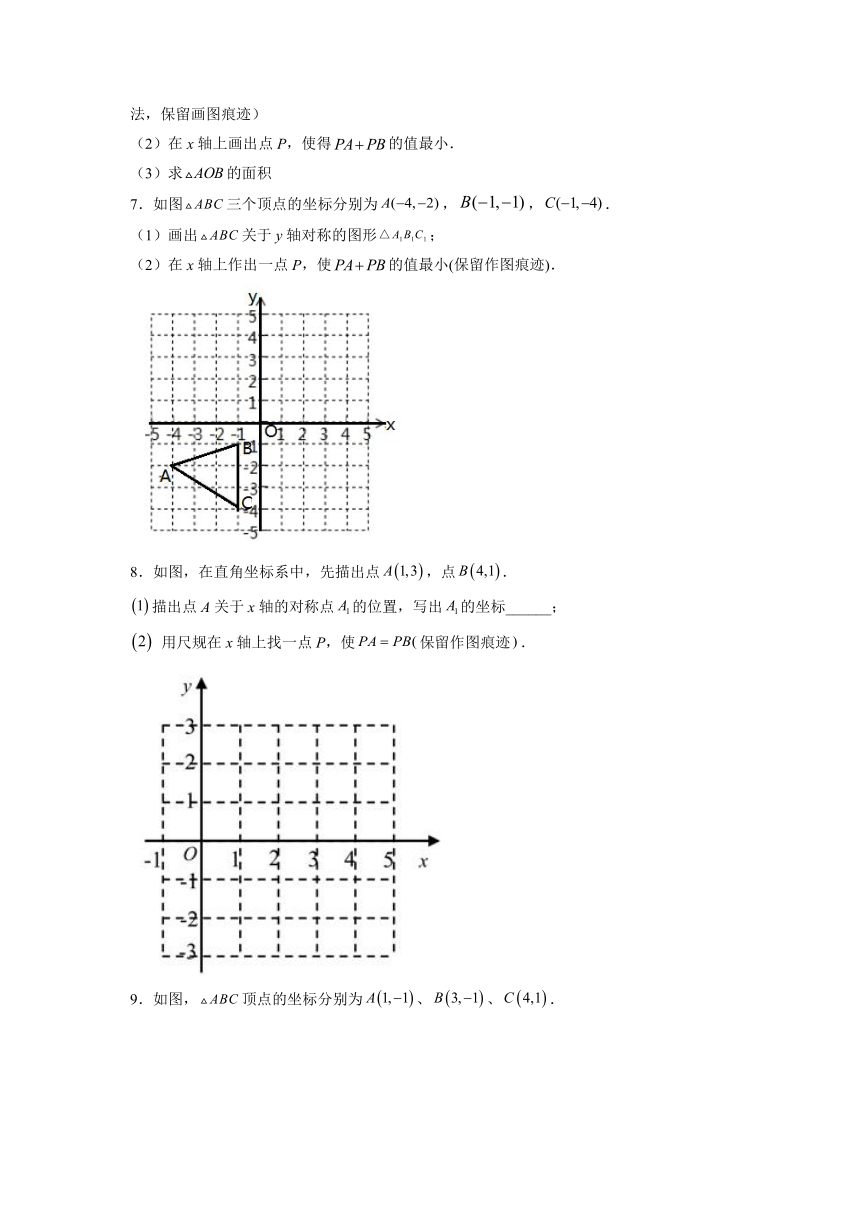
7.如图三个顶点的坐标分别为,,.
(1)画出关于y轴对称的图形;
(2)在x轴上作出一点P,使的值最小(保留作图痕迹).
8.如图,在直角坐标系中,先描出点,点.
描出点A关于x轴的对称点的位置,写出的坐标______;
用尺规在x轴上找一点P,使保留作图痕迹.
9.如图,顶点的坐标分别为、、.
(1)画出关于轴对称的三角形;
(2)若与全等(点与不重合),直接写出点的坐标;
(3)在如图所示网格范围内(包括边界),有格点,若,在图中画出,并写出点的坐标.
10.如图,已知△ABC的三个顶点在格点上,网格上最小的正方形的边长为1.
(1)点A关于x轴的对称点坐标为 ,点B关于y轴的对称点坐标为 .
(2)作出与△ABC关于x轴对称的图形△A1B1C1.
(3)求△ABC的面积.
参考答案
1.A
【分析】
根据轴对称图形的性质,横坐标互为相反数,纵坐标相等,即可得解.
【详解】
解:由题意,A,B关于y轴对称,
∵A(﹣5,3),
∴B(5,3),
故选:A.
【点睛】
此题主要考查平面直角坐标系中轴对称图形坐标的求解,熟练掌握,即可解题.
2.C
【分析】
由题意PQ∥x轴,所以过PQ中点且垂直于x轴的直线即为所求的直线,然后根据选项内容进行判断.
【详解】
解:∵点,点
∴PQ∥x轴,
设PQ的中点为M
则M点坐标为,即
∴点与点关于经过点且垂直于轴的直线对称
故选项A,B,D错误;
又∵在这条直线上,
∴选项C符合题意
故选:C.
【点睛】
本题考查点的坐标及轴对称,掌握轴对称的性质,利用数形结合思想解题是关键.
3.D
【分析】
根据坐标与距离的关系,坐标关于x轴,y轴对称的特点求解
【详解】
∵点A的坐标为,
∴点A到x轴的距离为|6|=6,到y轴的距离为|-5|=5,
∴选项A,B都是错误的;
∵点A关于x轴对称的点的坐标为,
∴选项C是错误的;
∵点A关于y轴对称的点的坐标为,
∴选项D是正确的;
故选D
【点睛】
本题考查了坐标的意义,坐标与距离,坐标与轴对称,准确理解坐标的意义,坐标的对称点的意义是解题的关键.
4.A
【分析】
根据A、B两点关于y轴对称,得到它们的横坐标互为相反数,纵坐标相等,列式求出m和n的值,就可以得出结果.
【详解】
解:∵点A和点B关于y轴对称,
∴,解得,
∴在第一象限.
故选:A.
【点睛】
本题考查点坐标的对称,解题的关键是掌握点坐标对称的特点.
5.3 1
【分析】
根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程求解即可.
【详解】
解:根据题意,得:
,
解得:,
故答案为:3,1.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.
6.(1)图见解析,点A1坐标为(1,2),点B1的坐标为( 2,1);(2)图见解析;(3).
【分析】
(1)利用关于y轴对称的点的坐标特征写出点A1和点B1的坐标,然后描点即可;
(2)作B点关于x轴的对称点B′,连接BB′交x轴于P点,利用两点之间线段最短可判断P点满足条件;
(3)用一个矩形的面积分别减去三个直角三角形的面积去计算的面积.
【详解】
(1)如图,△A1OB1为所作,点A1坐标为(1,2),点B1的坐标为( 2,1);
(2)如图,P点为所作;
(3)的面积=2×3 ×1×2 ×2×1 ×3×1=.
【点睛】
本题考查了作图 轴对称变换:几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.
7.(1)见解析;(2)见解析
【分析】
(1)先分别找出点A、B、C关于y轴的对称点,然后连接、、即可;
(2)找出点A关于x轴的对称点,然后连接,交x轴于点P,连接AP,根据两点之间线段最短即可说明点P即为所求.
【详解】
解:(1)先分别找出点A、B、C关于y轴的对称点,然后连接、、,如图所示,即为所求;
(2)找出点A关于x轴的对称点,然后连接,交x轴于点P,连接AP,
根据对称的性质,AP=
∴此时=,根据两点之间线段最短,此时最小
∴点P即为所求.
【点睛】
此题考查的是画已知图形关于y轴对称的图形和轴对称的性质,掌握画已知图形关于y轴对称的图形和两点之间线段最短是解决此题的关键.
8.(1);(2)见解析
【分析】
(1)直接利用关于直线对称点的性质得出对应点的位置进而得出答案;
(2)利用线段AB的垂直平分线的作法解答即可.
【详解】
(1);
(说明:描出A点,B点各1分,写出坐标2分)
(2)如图所示:点P即为所求.
【点睛】
本题考查了尺规作图的问题,掌握关于直线对称的点的性质、垂直平分线的作法是解题的关键.
9.(1)见解析;(2)(0,1)或(-4,-3)或(0,-3);(3)作图见解析,点M的坐标为(,2).
【分析】
(1)根据关于y轴对称的点的坐标特点画出关于轴对称的△A1B1C1即可;
(2)利用全等三角形的判定方法,写出D点坐标即可;
(3)根据网格结构找出点M的位置,然后连接OM即可,再根据平面直角坐标系写出点M的坐标即可.
【详解】
解:(1)如图所示:△A1B1C1,即为所求,
(2)如图所示△A1B1D1,△A1B1D2,△A1B1D3满足要求,
∴D1(0,1),D2(-4,-3),D3(0,-3);
(3)如图所示:AM⊥AC,点M即为所求,
此时,点M的坐标为(,2).
【点睛】
本题考查了轴对称变换以及全等三角形的判定,熟知轴对称的性质是解答此题的关键.
10.(1)(﹣2,﹣3),(3,2);(2)见解析;(3)S△ABC=1.5.
【分析】
(1)根据关于y轴对称点的坐标变化规律填空即可;
(2)根据轴对称的性质画图即可;
(3)用矩形面积减去三个三角形面积即可.
【详解】
解:(1)点A关于x轴的对称点坐标为(﹣2,﹣3),点B关于y轴的对称点坐标为(3,2)
故答案为:(﹣2,﹣3),(3,2).
(2)如图,△A1B1C1即为所求作.
(3)S△ABC=4﹣×1×2﹣×1×1﹣×1×2=1.5.
【点睛】
本题考查了轴对称的性质与作图,解题关键是熟知轴对称的作法和坐标变化规律,会用面积和差求三角形面积.
一、选择题
1.蝴蝶标本可以近似地看作轴对称图形,如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(﹣5,3),则其关于y轴对称的点B的坐标为( )
A.(5,3) B.(5,﹣3) C.(﹣5,﹣3) D.(3,5)
2.已知点与点关于某条直线对称,则这条直线是( )
A.轴 B.轴
C.过点且垂直于轴的直线 D.过点且平行于轴的直线
3.已知平面直角坐标系中点A的坐标为,则下列结论正确的是( )
A.点A到x轴的距离为5
B.点A到y轴的距离为6
C.点A关于x轴对称的点的坐标为
D.点A关于y轴对称的点的坐标为
4.若点与点关于轴对称,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
5.已知点A(m-l,-2)与点B(2,n+1)关于x轴对称,则m=______,n=______。
三、解答题
6.如图,在平面直角坐标系中,点,,.
(1)在图中画出关于y轴对称的,并直接写出点和点的坐标;(不写画法,保留画图痕迹)
(2)在x轴上画出点P,使得的值最小.
(3)求的面积
7.如图三个顶点的坐标分别为,,.
(1)画出关于y轴对称的图形;
(2)在x轴上作出一点P,使的值最小(保留作图痕迹).
8.如图,在直角坐标系中,先描出点,点.
描出点A关于x轴的对称点的位置,写出的坐标______;
用尺规在x轴上找一点P,使保留作图痕迹.
9.如图,顶点的坐标分别为、、.
(1)画出关于轴对称的三角形;
(2)若与全等(点与不重合),直接写出点的坐标;
(3)在如图所示网格范围内(包括边界),有格点,若,在图中画出,并写出点的坐标.
10.如图,已知△ABC的三个顶点在格点上,网格上最小的正方形的边长为1.
(1)点A关于x轴的对称点坐标为 ,点B关于y轴的对称点坐标为 .
(2)作出与△ABC关于x轴对称的图形△A1B1C1.
(3)求△ABC的面积.
参考答案
1.A
【分析】
根据轴对称图形的性质,横坐标互为相反数,纵坐标相等,即可得解.
【详解】
解:由题意,A,B关于y轴对称,
∵A(﹣5,3),
∴B(5,3),
故选:A.
【点睛】
此题主要考查平面直角坐标系中轴对称图形坐标的求解,熟练掌握,即可解题.
2.C
【分析】
由题意PQ∥x轴,所以过PQ中点且垂直于x轴的直线即为所求的直线,然后根据选项内容进行判断.
【详解】
解:∵点,点
∴PQ∥x轴,
设PQ的中点为M
则M点坐标为,即
∴点与点关于经过点且垂直于轴的直线对称
故选项A,B,D错误;
又∵在这条直线上,
∴选项C符合题意
故选:C.
【点睛】
本题考查点的坐标及轴对称,掌握轴对称的性质,利用数形结合思想解题是关键.
3.D
【分析】
根据坐标与距离的关系,坐标关于x轴,y轴对称的特点求解
【详解】
∵点A的坐标为,
∴点A到x轴的距离为|6|=6,到y轴的距离为|-5|=5,
∴选项A,B都是错误的;
∵点A关于x轴对称的点的坐标为,
∴选项C是错误的;
∵点A关于y轴对称的点的坐标为,
∴选项D是正确的;
故选D
【点睛】
本题考查了坐标的意义,坐标与距离,坐标与轴对称,准确理解坐标的意义,坐标的对称点的意义是解题的关键.
4.A
【分析】
根据A、B两点关于y轴对称,得到它们的横坐标互为相反数,纵坐标相等,列式求出m和n的值,就可以得出结果.
【详解】
解:∵点A和点B关于y轴对称,
∴,解得,
∴在第一象限.
故选:A.
【点睛】
本题考查点坐标的对称,解题的关键是掌握点坐标对称的特点.
5.3 1
【分析】
根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程求解即可.
【详解】
解:根据题意,得:
,
解得:,
故答案为:3,1.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.
6.(1)图见解析,点A1坐标为(1,2),点B1的坐标为( 2,1);(2)图见解析;(3).
【分析】
(1)利用关于y轴对称的点的坐标特征写出点A1和点B1的坐标,然后描点即可;
(2)作B点关于x轴的对称点B′,连接BB′交x轴于P点,利用两点之间线段最短可判断P点满足条件;
(3)用一个矩形的面积分别减去三个直角三角形的面积去计算的面积.
【详解】
(1)如图,△A1OB1为所作,点A1坐标为(1,2),点B1的坐标为( 2,1);
(2)如图,P点为所作;
(3)的面积=2×3 ×1×2 ×2×1 ×3×1=.
【点睛】
本题考查了作图 轴对称变换:几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.
7.(1)见解析;(2)见解析
【分析】
(1)先分别找出点A、B、C关于y轴的对称点,然后连接、、即可;
(2)找出点A关于x轴的对称点,然后连接,交x轴于点P,连接AP,根据两点之间线段最短即可说明点P即为所求.
【详解】
解:(1)先分别找出点A、B、C关于y轴的对称点,然后连接、、,如图所示,即为所求;
(2)找出点A关于x轴的对称点,然后连接,交x轴于点P,连接AP,
根据对称的性质,AP=
∴此时=,根据两点之间线段最短,此时最小
∴点P即为所求.
【点睛】
此题考查的是画已知图形关于y轴对称的图形和轴对称的性质,掌握画已知图形关于y轴对称的图形和两点之间线段最短是解决此题的关键.
8.(1);(2)见解析
【分析】
(1)直接利用关于直线对称点的性质得出对应点的位置进而得出答案;
(2)利用线段AB的垂直平分线的作法解答即可.
【详解】
(1);
(说明:描出A点,B点各1分,写出坐标2分)
(2)如图所示:点P即为所求.
【点睛】
本题考查了尺规作图的问题,掌握关于直线对称的点的性质、垂直平分线的作法是解题的关键.
9.(1)见解析;(2)(0,1)或(-4,-3)或(0,-3);(3)作图见解析,点M的坐标为(,2).
【分析】
(1)根据关于y轴对称的点的坐标特点画出关于轴对称的△A1B1C1即可;
(2)利用全等三角形的判定方法,写出D点坐标即可;
(3)根据网格结构找出点M的位置,然后连接OM即可,再根据平面直角坐标系写出点M的坐标即可.
【详解】
解:(1)如图所示:△A1B1C1,即为所求,
(2)如图所示△A1B1D1,△A1B1D2,△A1B1D3满足要求,
∴D1(0,1),D2(-4,-3),D3(0,-3);
(3)如图所示:AM⊥AC,点M即为所求,
此时,点M的坐标为(,2).
【点睛】
本题考查了轴对称变换以及全等三角形的判定,熟知轴对称的性质是解答此题的关键.
10.(1)(﹣2,﹣3),(3,2);(2)见解析;(3)S△ABC=1.5.
【分析】
(1)根据关于y轴对称点的坐标变化规律填空即可;
(2)根据轴对称的性质画图即可;
(3)用矩形面积减去三个三角形面积即可.
【详解】
解:(1)点A关于x轴的对称点坐标为(﹣2,﹣3),点B关于y轴的对称点坐标为(3,2)
故答案为:(﹣2,﹣3),(3,2).
(2)如图,△A1B1C1即为所求作.
(3)S△ABC=4﹣×1×2﹣×1×1﹣×1×2=1.5.
【点睛】
本题考查了轴对称的性质与作图,解题关键是熟知轴对称的作法和坐标变化规律,会用面积和差求三角形面积.
