第十二章全等三角形 12.3角的平分线的性质 同步练习题 2021-2022学年 人教版八年级数学上册 (word版含答案)
文档属性
| 名称 | 第十二章全等三角形 12.3角的平分线的性质 同步练习题 2021-2022学年 人教版八年级数学上册 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 08:33:37 | ||
图片预览




文档简介
2021——2022学年度人教版八年级数学上册 第十二章全等三角形 12.3角的平分线的性质 同步练习题
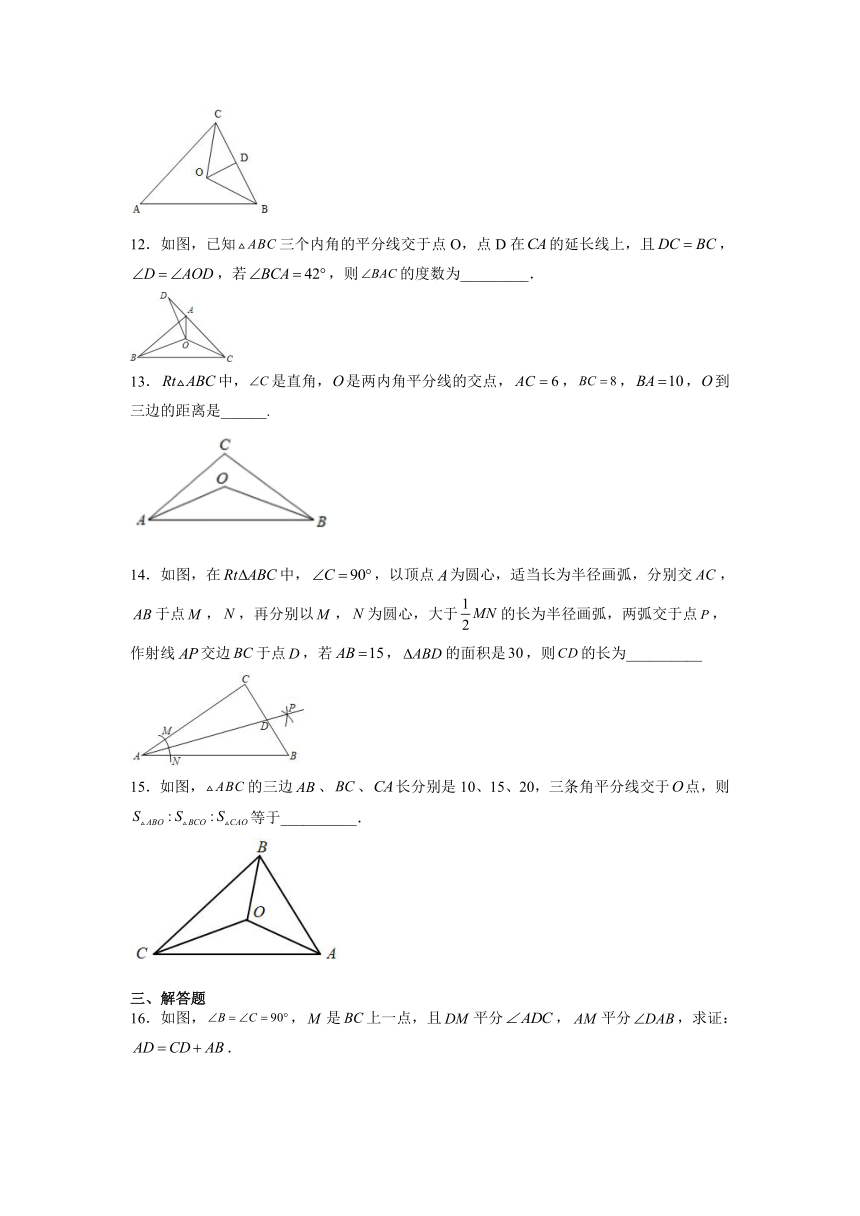
一、选择题
1.如图,,分别是,上的点,过点作于点,作于点,若,,则下面三个结论:①;②;③,正确的是( )
A.①③ B.②③ C.①② D.①②③
2.如图,中,,AD平分,,,垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④.其中正确的是( )
A.②④ B.②④ C.②③④ D.①②③④
3.如图,AD平分,于点E,于点F,则下列结论不正确的是( )
A.△AEG≌△AFG B.△AED≌△AFD C.△DEG≌△DFG D.△BDE≌△CDF
4.如图,已知,点O为与的平分线的交点,且于D.若,则四边形ABOC的面积是( )
A.36 B.32 C.30 D.64
5.如图,平分,于点,于点,延长,交, 于点,,下列结论错误的是( )
A. B. C. D.
6.如图所示,已知AB∥CD,与的平分线交于点,于点,且,则点到,的距离之和是( )
A. B. C. D.
7.如图,是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.
A. B. C. D.
8.已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
A.BD+ED=BC B.DE平分∠ADB C.AD平分∠EDC D.ED+AC>AD
9.如图,在中,,是的角平分线,是边上一点,若,则的长可以是( )
A.1 B.3 C.5 D.7
10.如图,是的角平分线, ,则与的面积比为( ).
A. B. C. D.
二、填空题
11.如图,在中,的平分线交于点O,于D,如果,,,且S△ABC=150cm2,那么_____.
12.如图,已知三个内角的平分线交于点O,点D在的延长线上,且,,若,则的度数为_________.
13.中,是直角,是两内角平分线的交点,,,,到三边的距离是______.
14.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,的面积是,则的长为__________
15.如图,的三边、、长分别是10、15、20,三条角平分线交于点,则等于__________.
三、解答题
16.如图,,是上一点,且平分,平分,求证:.
17.已知:如图,在中,,BD平分,于点E,若与的面积比为,求与的面积之比.
18.如图,在△ABC中,GD=DC,过点G作FG∥BC交BD的延长线于点F,交AB于点E.
(1)△DFG与△DBC全等吗?说明理由;
(2)当∠C=90°,DE⊥BD,CD=2时,求点D到AB边的距离.
19.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB;
(2)若AB=14,AF=8,求CF的长.
20.如图,在中,平分,,于点,点在上,.
(1)求证:;
(2)若,,求的长.
21.如图,四边形中,,点为的中点,且平分,,垂足为点
(1)求证:平分;
(2)求证:;
(3)判断,,之间的数量关系,并说明理由.
22.已知是的平分线,点是射线上点,点,分别在射线,上,连接,.
(1)发现问题:如图1,当,时,则与的数量关系是 .
(2)探究问题:如图2,点,在射线,上滑动,且,当时,与在(1)中的数量关系还成立吗?说明理由.(温馨提示:过作于,于)
23.(1)如图1,中,的角平分线与的外角的平分线交于.当为时,则为的度数.
(2)在(1)的条件下,若的角平分线与的角平分线交于,与的平分线交于,如此继续下去可得…,,则______°;
(3)如图2,四边形ABCD中,为的角平分线及外角的平分线所在的直线构成的角,若,则_________°;
(4)如图3,中,的角平分线与的外角的平分线交于,若E为BA延长线上一动点,连EC,与的角平分线交于Q,
①求证的值为定值;
②的值为定值.其中有且只有一个是正确的,请写出正确的结论 (填编号),并写出其值.
【参考答案】
1.C 2.D 3.D 4.B 5.D 6.B 7.D 8.B 9.D 10.A
11.5
12.92°
13.2
14.4
15.
16.证明:如图:
过作于,
,平分,平分,
,,,,,,
在和中,
,
,
,
同理:AE=AB,
.
17.∵BD平分,,
∴DE=DC
∵BD=BD
∴Rt△DBE≌Rt△DBC(HL)
∴△DBE与△DBC的面积相等
∵与的面积比为
设的面积为3k,则的面积为8k
∴△DBE的面积为3k,△ADE的面积为:8k-3k-3k=2k
∴与的面积之比为:2k:8k=1:4.
18.解:(1)△DFG≌△DBC,理由如下:
∵FG∥BC,
∴∠F=∠FBC,
在△DFG和△DBC中,
∵,
∴△DFG≌△DBC(AAS).
(2)如图,过点D作DM⊥AB于点M,连结DE,
由(1)得△DFG≌△DBC,
∴DF=DB,
∵DE⊥BD,
∴∠EDF=∠EDB=90°,
在△DEF和△DEB中,
∵,
∴△DEF≌△DEB(SAS),
∴∠F=∠EBD,
∵FG∥BC,
∴∠F=∠FBC,
∴∠EBD=∠FBC,
∴BD平分∠ABC,
∵∠C=90°,
∴DC⊥BC,
∵DM⊥AB,CD=2,
∴DM=CD=2,即点D到AB边的距离为2.
19.(1)∵DE⊥AB于点E,
∴∠DEB=90°,
又AD平分∠BAC,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB(HL),
∴CF=EB.
(2)在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
设CF=BE=x,则AE=AB﹣BE=14﹣x,AC=AF+CF=8+x,
∴14﹣x=8+x,解得:x=3.
故CF=3.
20.解:(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)设CF=x,则AE=14-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=14-x,
解得x=3,即CF=3.
21.证明:∵,平分,OE⊥AC,
∴.
∵点为的中点,
∴,
∴,
∴平分.
证明:在和中,
,
∴,
∴.
同理求出,
∴,
∴.
解:.
理由如下:
∵,
∴.
同理可得.
∵,
∴.
22.解:(1)PC=PD,
理由:∵OM是∠AOB的平分线,,
∴PC=PD(角平分线上点到角两边的距离相等),
故答案为:PC=PD;
(2)成立
理由:过点P点作PE⊥OA于E,PF⊥OB于F,如图,
∴∠PEC=∠PFD=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF,
在△PCE和△PDF中
∴△PCE≌△PDF(AAS),
∴PC=PD.
23.解:(1)∵的角平分线与的外角的平分线交于,
∴∠1=∠2,∠3=∠4,
∵∠4=∠2+∠A1,∠ACD=∠A+∠ABC,即∠3+∠4=∠A+∠1+∠2,
∴2∠4=∠A+2∠2,
整理得∠4=∠A+∠2,
∴∠A1=∠A=;
(2)由(1)得∠A1=∠A,∠A2=∠A1,∠A3=∠A2…,
∴∠A2=∠A1=∠A,
∴∠A3=∠A2=∠A=∠A,
…,
∴∠An=∠A,
∴当n=6时∠A6=∠A=,
故答案为:;
(3)延长BA,CD交于G,
∵,
∴∠GAD+∠GDA=360°-()=360°-230°=130°,
∴∠G=180°-(∠GAD+∠GDA)=180°-130°=50°,
∴∠F=∠G=;
(4)①=180°,
∵∠A1=∠BAC,
∵∠Q=180°-∠6-∠8,QE平分∠AEC,QC平分∠ACE,
∴∠5=∠6,,7=∠8,
∵∠EAC+∠5+∠6+∠7+∠8=180°,
∴∠EAC+2∠6+2∠8=180°,
∴∠6+∠8=90°-∠EAC,
∴∠Q=180°-(∠6+∠8)=180°-(90°-∠EAC)=90°+∠EAC,
∴=90°+∠EAC+∠BAC=90°+(∠EAC+∠BAC)=90°+90°=180°,
∴的值为定值,
②==90°+∠EAC-∠BAC=90°+(∠EAC-∠BAC),
∵∠EAC=180°-∠BAC,
∴=90°+(180°-∠BAC -∠BAC)=180°-∠BAC,
∵∠BAC可变,
∴的值不为定值.
故答案为①, ∠Q+∠A=180°.
一、选择题
1.如图,,分别是,上的点,过点作于点,作于点,若,,则下面三个结论:①;②;③,正确的是( )
A.①③ B.②③ C.①② D.①②③
2.如图,中,,AD平分,,,垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④.其中正确的是( )
A.②④ B.②④ C.②③④ D.①②③④
3.如图,AD平分,于点E,于点F,则下列结论不正确的是( )
A.△AEG≌△AFG B.△AED≌△AFD C.△DEG≌△DFG D.△BDE≌△CDF
4.如图,已知,点O为与的平分线的交点,且于D.若,则四边形ABOC的面积是( )
A.36 B.32 C.30 D.64
5.如图,平分,于点,于点,延长,交, 于点,,下列结论错误的是( )
A. B. C. D.
6.如图所示,已知AB∥CD,与的平分线交于点,于点,且,则点到,的距离之和是( )
A. B. C. D.
7.如图,是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.
A. B. C. D.
8.已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
A.BD+ED=BC B.DE平分∠ADB C.AD平分∠EDC D.ED+AC>AD
9.如图,在中,,是的角平分线,是边上一点,若,则的长可以是( )
A.1 B.3 C.5 D.7
10.如图,是的角平分线, ,则与的面积比为( ).
A. B. C. D.
二、填空题
11.如图,在中,的平分线交于点O,于D,如果,,,且S△ABC=150cm2,那么_____.
12.如图,已知三个内角的平分线交于点O,点D在的延长线上,且,,若,则的度数为_________.
13.中,是直角,是两内角平分线的交点,,,,到三边的距离是______.
14.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,若,的面积是,则的长为__________
15.如图,的三边、、长分别是10、15、20,三条角平分线交于点,则等于__________.
三、解答题
16.如图,,是上一点,且平分,平分,求证:.
17.已知:如图,在中,,BD平分,于点E,若与的面积比为,求与的面积之比.
18.如图,在△ABC中,GD=DC,过点G作FG∥BC交BD的延长线于点F,交AB于点E.
(1)△DFG与△DBC全等吗?说明理由;
(2)当∠C=90°,DE⊥BD,CD=2时,求点D到AB边的距离.
19.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB;
(2)若AB=14,AF=8,求CF的长.
20.如图,在中,平分,,于点,点在上,.
(1)求证:;
(2)若,,求的长.
21.如图,四边形中,,点为的中点,且平分,,垂足为点
(1)求证:平分;
(2)求证:;
(3)判断,,之间的数量关系,并说明理由.
22.已知是的平分线,点是射线上点,点,分别在射线,上,连接,.
(1)发现问题:如图1,当,时,则与的数量关系是 .
(2)探究问题:如图2,点,在射线,上滑动,且,当时,与在(1)中的数量关系还成立吗?说明理由.(温馨提示:过作于,于)
23.(1)如图1,中,的角平分线与的外角的平分线交于.当为时,则为的度数.
(2)在(1)的条件下,若的角平分线与的角平分线交于,与的平分线交于,如此继续下去可得…,,则______°;
(3)如图2,四边形ABCD中,为的角平分线及外角的平分线所在的直线构成的角,若,则_________°;
(4)如图3,中,的角平分线与的外角的平分线交于,若E为BA延长线上一动点,连EC,与的角平分线交于Q,
①求证的值为定值;
②的值为定值.其中有且只有一个是正确的,请写出正确的结论 (填编号),并写出其值.
【参考答案】
1.C 2.D 3.D 4.B 5.D 6.B 7.D 8.B 9.D 10.A
11.5
12.92°
13.2
14.4
15.
16.证明:如图:
过作于,
,平分,平分,
,,,,,,
在和中,
,
,
,
同理:AE=AB,
.
17.∵BD平分,,
∴DE=DC
∵BD=BD
∴Rt△DBE≌Rt△DBC(HL)
∴△DBE与△DBC的面积相等
∵与的面积比为
设的面积为3k,则的面积为8k
∴△DBE的面积为3k,△ADE的面积为:8k-3k-3k=2k
∴与的面积之比为:2k:8k=1:4.
18.解:(1)△DFG≌△DBC,理由如下:
∵FG∥BC,
∴∠F=∠FBC,
在△DFG和△DBC中,
∵,
∴△DFG≌△DBC(AAS).
(2)如图,过点D作DM⊥AB于点M,连结DE,
由(1)得△DFG≌△DBC,
∴DF=DB,
∵DE⊥BD,
∴∠EDF=∠EDB=90°,
在△DEF和△DEB中,
∵,
∴△DEF≌△DEB(SAS),
∴∠F=∠EBD,
∵FG∥BC,
∴∠F=∠FBC,
∴∠EBD=∠FBC,
∴BD平分∠ABC,
∵∠C=90°,
∴DC⊥BC,
∵DM⊥AB,CD=2,
∴DM=CD=2,即点D到AB边的距离为2.
19.(1)∵DE⊥AB于点E,
∴∠DEB=90°,
又AD平分∠BAC,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB(HL),
∴CF=EB.
(2)在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
设CF=BE=x,则AE=AB﹣BE=14﹣x,AC=AF+CF=8+x,
∴14﹣x=8+x,解得:x=3.
故CF=3.
20.解:(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)设CF=x,则AE=14-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=14-x,
解得x=3,即CF=3.
21.证明:∵,平分,OE⊥AC,
∴.
∵点为的中点,
∴,
∴,
∴平分.
证明:在和中,
,
∴,
∴.
同理求出,
∴,
∴.
解:.
理由如下:
∵,
∴.
同理可得.
∵,
∴.
22.解:(1)PC=PD,
理由:∵OM是∠AOB的平分线,,
∴PC=PD(角平分线上点到角两边的距离相等),
故答案为:PC=PD;
(2)成立
理由:过点P点作PE⊥OA于E,PF⊥OB于F,如图,
∴∠PEC=∠PFD=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF,
在△PCE和△PDF中
∴△PCE≌△PDF(AAS),
∴PC=PD.
23.解:(1)∵的角平分线与的外角的平分线交于,
∴∠1=∠2,∠3=∠4,
∵∠4=∠2+∠A1,∠ACD=∠A+∠ABC,即∠3+∠4=∠A+∠1+∠2,
∴2∠4=∠A+2∠2,
整理得∠4=∠A+∠2,
∴∠A1=∠A=;
(2)由(1)得∠A1=∠A,∠A2=∠A1,∠A3=∠A2…,
∴∠A2=∠A1=∠A,
∴∠A3=∠A2=∠A=∠A,
…,
∴∠An=∠A,
∴当n=6时∠A6=∠A=,
故答案为:;
(3)延长BA,CD交于G,
∵,
∴∠GAD+∠GDA=360°-()=360°-230°=130°,
∴∠G=180°-(∠GAD+∠GDA)=180°-130°=50°,
∴∠F=∠G=;
(4)①=180°,
∵∠A1=∠BAC,
∵∠Q=180°-∠6-∠8,QE平分∠AEC,QC平分∠ACE,
∴∠5=∠6,,7=∠8,
∵∠EAC+∠5+∠6+∠7+∠8=180°,
∴∠EAC+2∠6+2∠8=180°,
∴∠6+∠8=90°-∠EAC,
∴∠Q=180°-(∠6+∠8)=180°-(90°-∠EAC)=90°+∠EAC,
∴=90°+∠EAC+∠BAC=90°+(∠EAC+∠BAC)=90°+90°=180°,
∴的值为定值,
②==90°+∠EAC-∠BAC=90°+(∠EAC-∠BAC),
∵∠EAC=180°-∠BAC,
∴=90°+(180°-∠BAC -∠BAC)=180°-∠BAC,
∵∠BAC可变,
∴的值不为定值.
故答案为①, ∠Q+∠A=180°.
