探索勾股定理1
图片预览

文档简介
(共25张PPT)
勾股定理
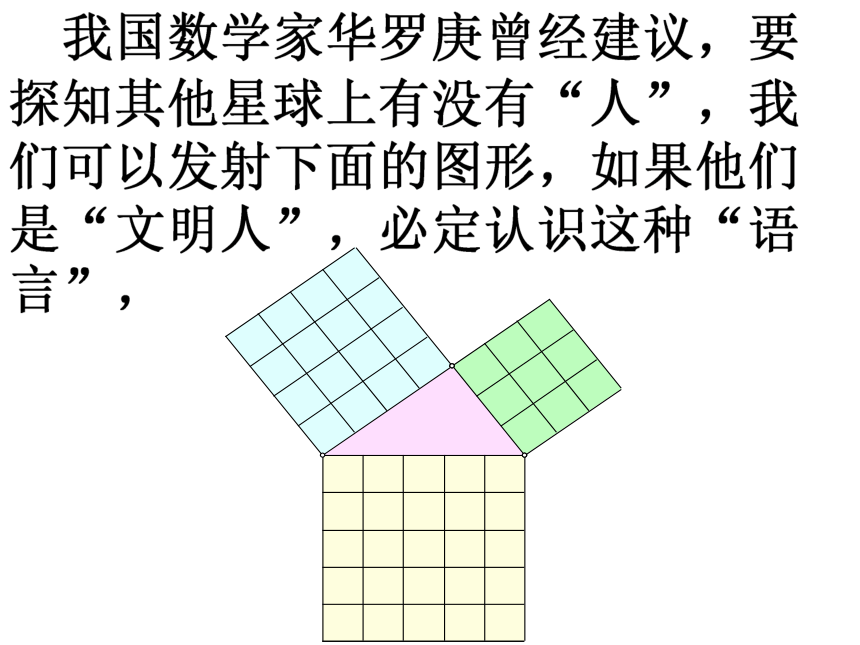
我国数学家华罗庚曾经建议,要探知其他星球上有没有“人”,我们可以发射下面的图形,如果他们是“文明人”,必定认识这种“语言”,
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
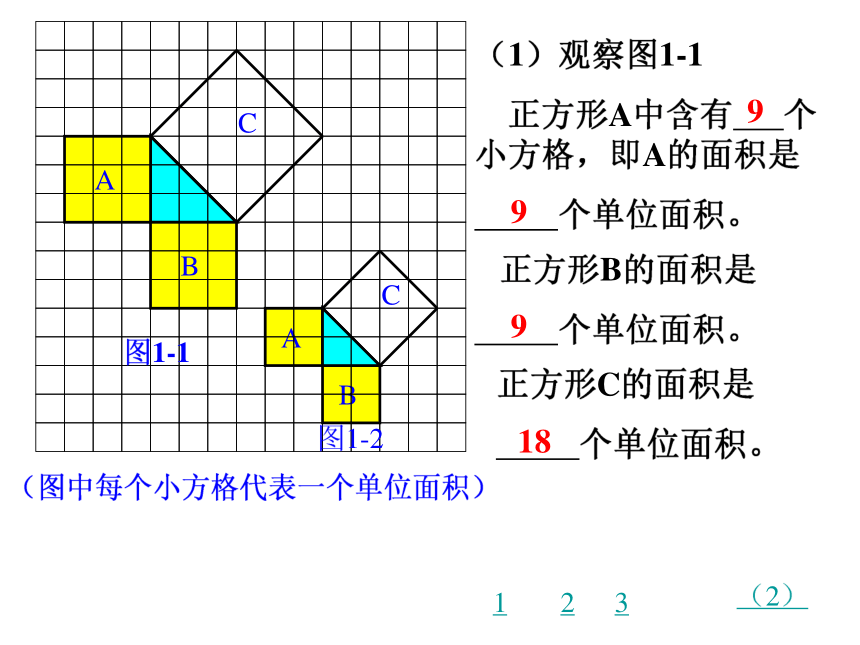
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
1
2
3
(2)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
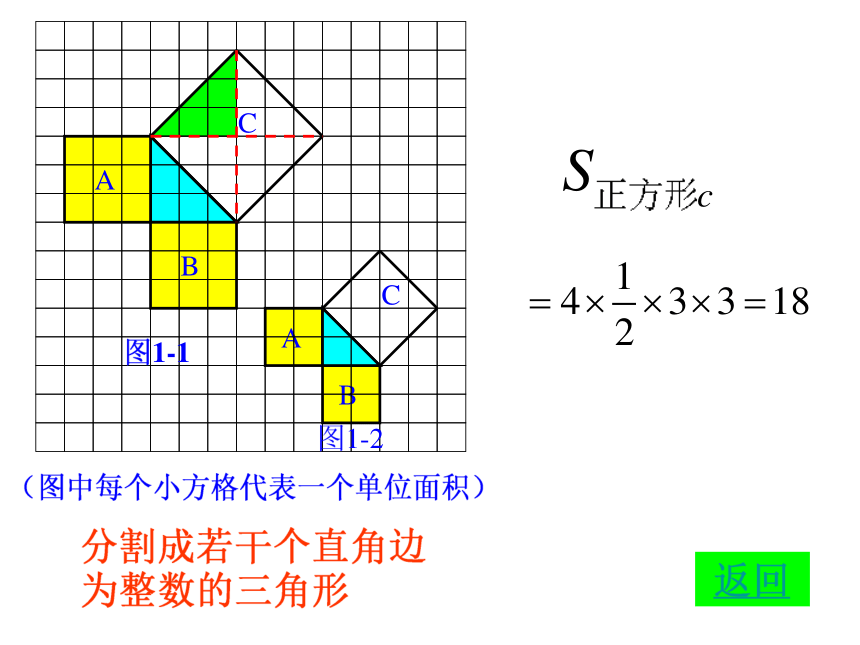
分割成若干个直角边为整数的三角形
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
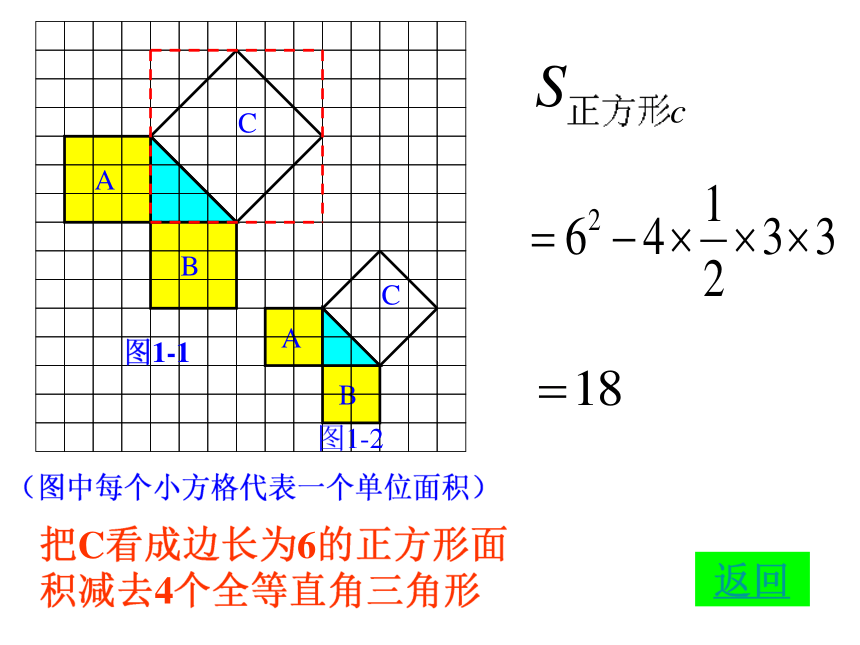
把C看成边长为6的正方形面积减去4个全等直角三角形
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
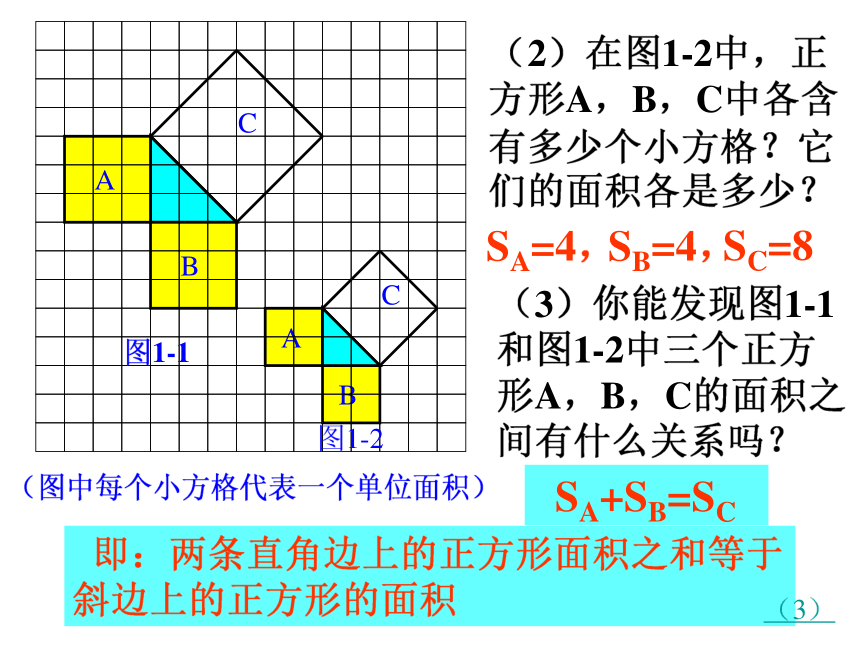
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1和图1-2中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
(3)
SA=4,
SB=4,
SC=8
A
B
C
图1-3
A
B
C
图1-4
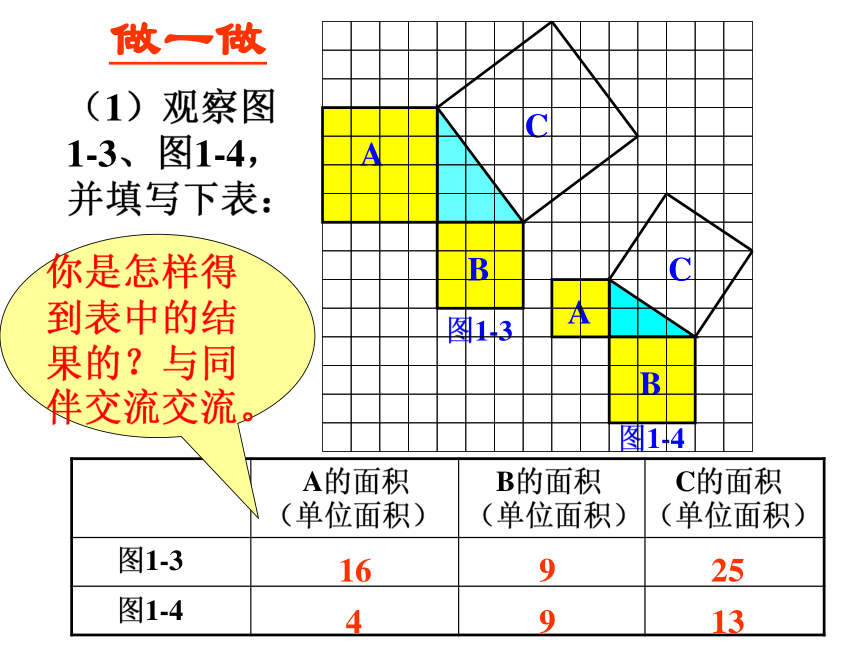
(1)观察图1-3、图1-4,并填写下表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流。
做一做
A
B
C
图1-3
A
B
C
图1-4
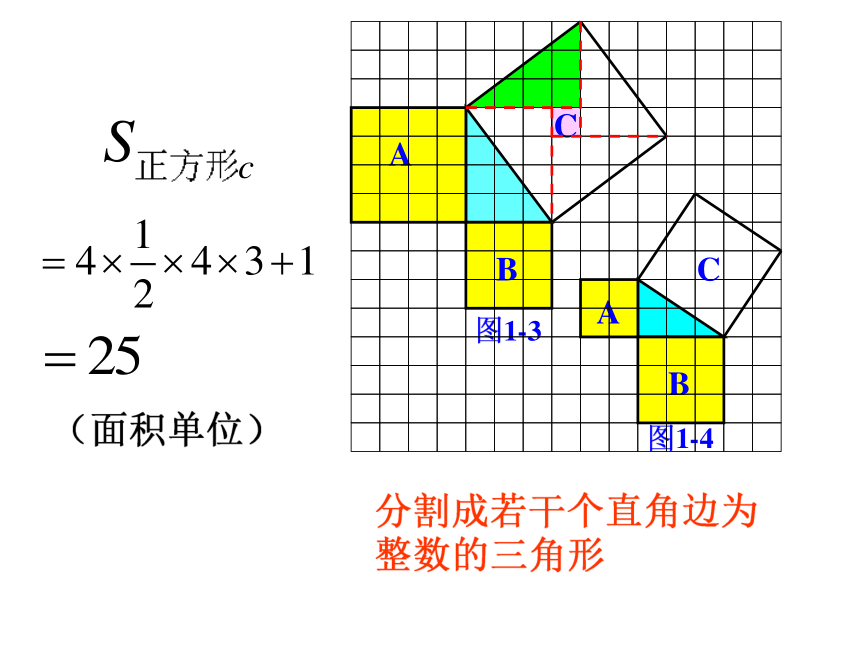
分割成若干个直角边为整数的三角形
(面积单位)
A
B
C
图1-3
A
B
C
图1-4
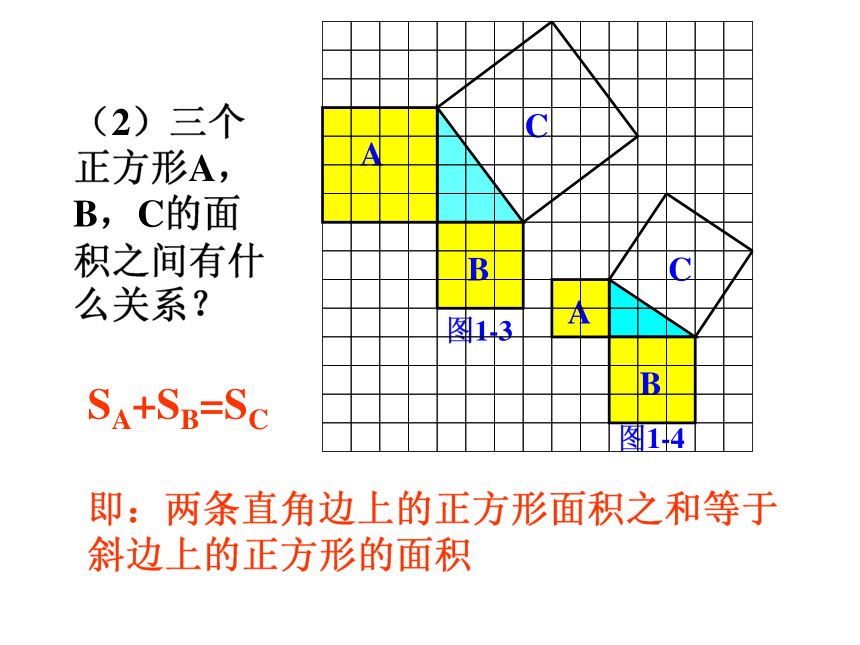
(2)三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
A
B
C
图1-3
A
B
C
图1-4
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
(3)分别以6厘米、8厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?
议一议
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
证法一:
1、整体看
2、分割看
a
b
c
弦图
证法二:
1、整体看
2、分割看
b-a
证法三:
a
a
b
b
c
c
伽菲尔德证法:
1、整体看
2、分割看
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
勾股定理的应用:已知直角三角形的两边求第三边。
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
c=10
b=9
a=12
a=9,b=12
例2:在Rt△ABC中, a=6,b=8,试求第三边c的值
直角三角形中,如果没有说明哪个角是90°,要注意分类讨论。
方法小结
c=10或c=
8
6
A
C
B
8
6
C
A
B
1、求下图中字母所代表的正方形的面积。
225
400
A
625
练习:
两条直角边上的正方形面积之和等于斜边上的正方形的面积
方法小结:
2、求出下列直角三角形中未知的边
A
B
C
6
10
可用勾股定理建立方程.
方法小结:
A
B
C
x=8
如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
3、
9米
5 或
4、已知:Rt△ABC中,有两条边为4和3,则第三条边的长为__________.
4
3
A
C
B
4
3
C
A
B
5、如图:在Rt△ABC中, ∠c=900, ∠A=150, BC=1,则求AC的长.
C
A
B
D
150
1
提示:作辅助线BD使∠ABD=150 ,则推出∠BDC=300 ,可得:BD=2,求得CD=
有AD=BD=2,可得AC=2+
300
小结
说说这节课你有什么收获?
内容总结:探索直角三角形两直角边的平方和等于斜边的平方;利用勾股定理解决实际问题。
方法总结:
①数方格看图找关系,利用面积不变的方法;
②用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
再见
C
A
B
A
B
C
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
勾股定理
我国数学家华罗庚曾经建议,要探知其他星球上有没有“人”,我们可以发射下面的图形,如果他们是“文明人”,必定认识这种“语言”,
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
1
2
3
(2)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
把C看成边长为6的正方形面积减去4个全等直角三角形
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1-1和图1-2中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
(3)
SA=4,
SB=4,
SC=8
A
B
C
图1-3
A
B
C
图1-4
(1)观察图1-3、图1-4,并填写下表:
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流。
做一做
A
B
C
图1-3
A
B
C
图1-4
分割成若干个直角边为整数的三角形
(面积单位)
A
B
C
图1-3
A
B
C
图1-4
(2)三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
A
B
C
图1-3
A
B
C
图1-4
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
(3)分别以6厘米、8厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?
议一议
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
证法一:
1、整体看
2、分割看
a
b
c
弦图
证法二:
1、整体看
2、分割看
b-a
证法三:
a
a
b
b
c
c
伽菲尔德证法:
1、整体看
2、分割看
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
勾股定理的应用:已知直角三角形的两边求第三边。
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
c=10
b=9
a=12
a=9,b=12
例2:在Rt△ABC中, a=6,b=8,试求第三边c的值
直角三角形中,如果没有说明哪个角是90°,要注意分类讨论。
方法小结
c=10或c=
8
6
A
C
B
8
6
C
A
B
1、求下图中字母所代表的正方形的面积。
225
400
A
625
练习:
两条直角边上的正方形面积之和等于斜边上的正方形的面积
方法小结:
2、求出下列直角三角形中未知的边
A
B
C
6
10
可用勾股定理建立方程.
方法小结:
A
B
C
x=8
如图,受台风“麦莎”影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
3、
9米
5 或
4、已知:Rt△ABC中,有两条边为4和3,则第三条边的长为__________.
4
3
A
C
B
4
3
C
A
B
5、如图:在Rt△ABC中, ∠c=900, ∠A=150, BC=1,则求AC的长.
C
A
B
D
150
1
提示:作辅助线BD使∠ABD=150 ,则推出∠BDC=300 ,可得:BD=2,求得CD=
有AD=BD=2,可得AC=2+
300
小结
说说这节课你有什么收获?
内容总结:探索直角三角形两直角边的平方和等于斜边的平方;利用勾股定理解决实际问题。
方法总结:
①数方格看图找关系,利用面积不变的方法;
②用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
再见
C
A
B
A
B
C
正方形周边上的格点数a=12
正方形内部的格点数b=13
利用皮克公式
所以,正方形C的面积为:
(单位面积)
返回
图1-1
图1-2
