13.3.2 等边三角形 课件(共26张PPT)
文档属性
| 名称 | 13.3.2 等边三角形 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-11 10:00:24 | ||
图片预览




文档简介
(共26张PPT)
人教版 八年级上
13.3.2 等边三角形
1、我们是怎样研究等腰三角形的?
定义 性质 判定
性质:边 角 特殊线段 对称性
2、我们可以从哪些方面研究等边三角形呢?
3、一个三角形满足什么条件就是等边三角形?
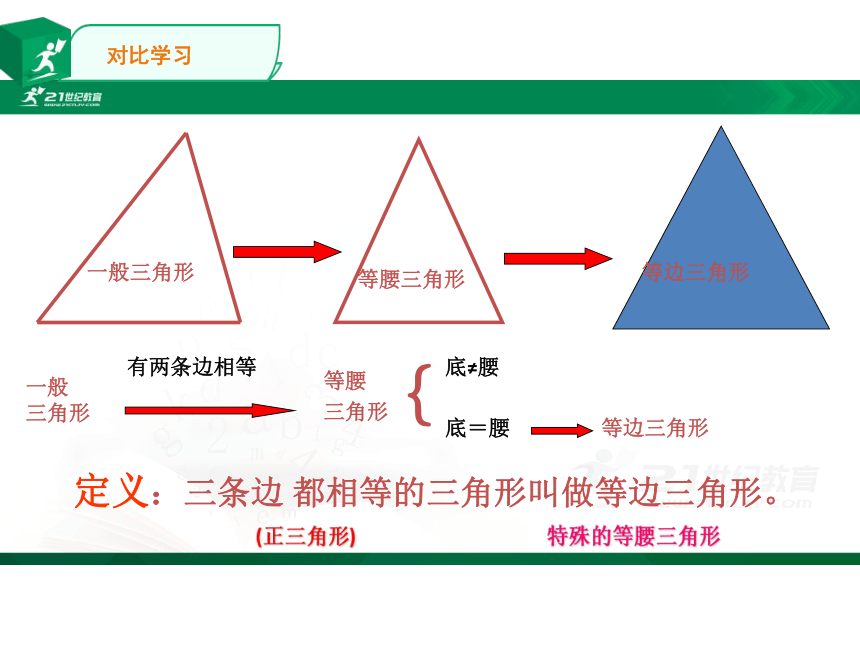
对比学习
等腰三角形
等边三角形
一般
三角形
定义:三条边 都相等的三角形叫做等边三角形。
特殊的等腰三角形
一般三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
{
(正三角形)
对比学习
小明假设等腰三角形底角为60°,得出了三个角都是60°,小亮假设顶角为60°,也得出了三个角都是60°,根据“等角对等边”,最后得出结论:三边都相等。
老师告诉他们“这种三条边都相等的叫做等边三角形”。小明、小亮也发表了自己的看法, 小明认为“三条边都相等的三角形是等边三角形,而不是等腰三角形”;小亮认为“等边三角形也还是等腰三角形,只是比一般的等腰三角形特殊而已”., 小明、小亮谁说的有道理呢?学完这节课就能见分晓。
情景导入
活动1: 探究等边三角形的性质
1.等边三角形边、角具有什么性质?
2.等边三角形有“三线合一”的性质吗 为什么
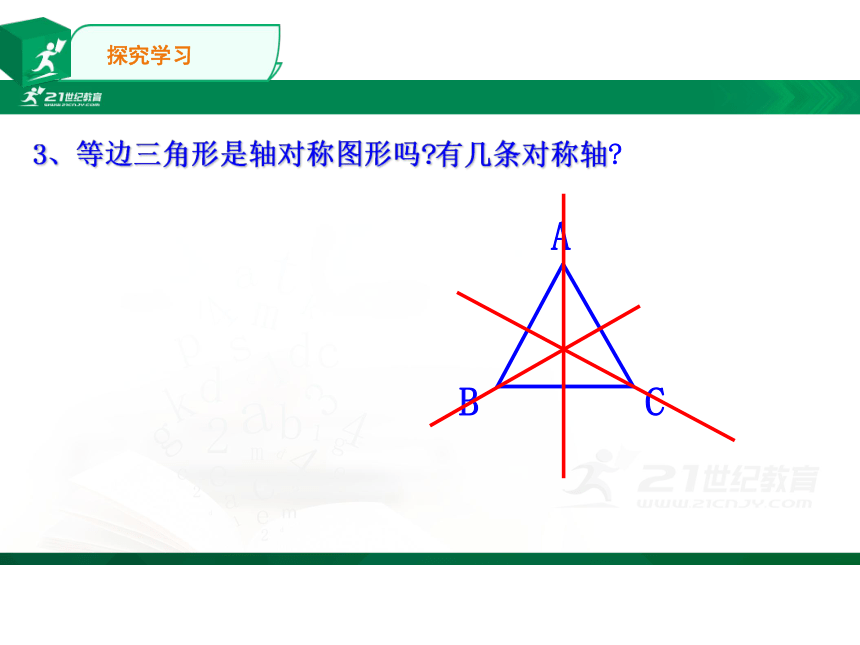
3.等边三角形是轴对称图形吗?有几条对称轴?
探究学习
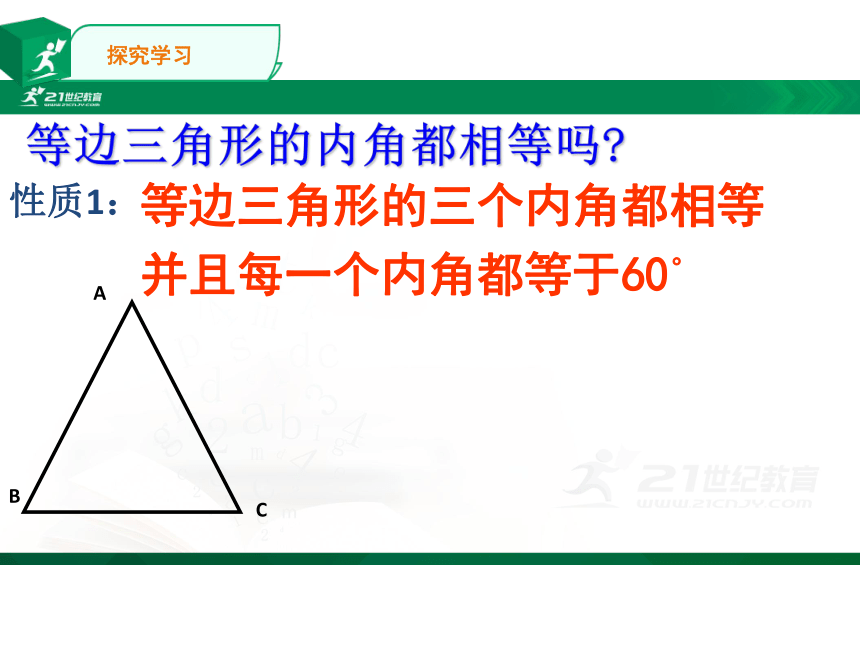
等边三角形的三个内角都相等
并且每一个内角都等于60。
A
B
C
性质1:
等边三角形的内角都相等吗
探究学习
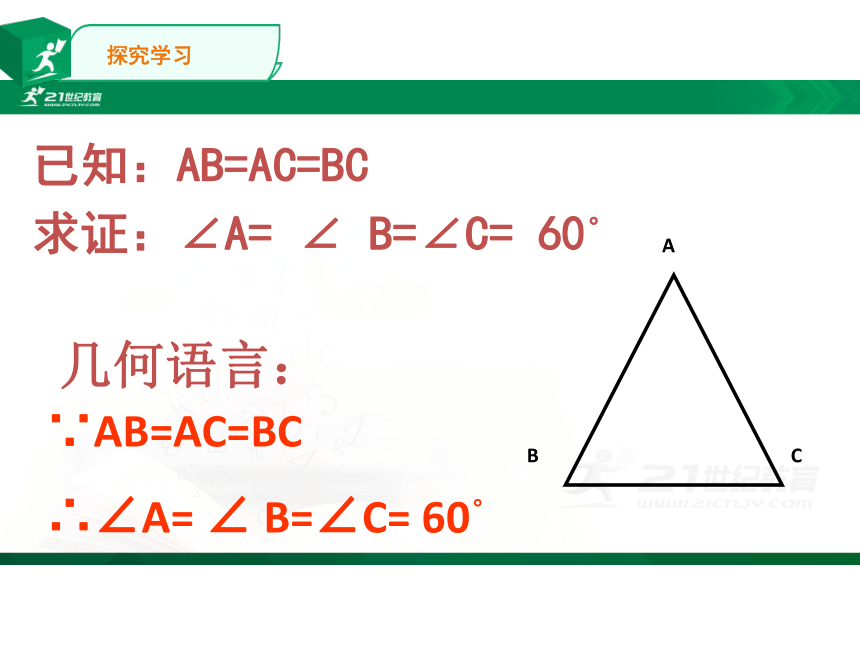
∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。
几何语言:
已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60。
A
B
C
探究学习
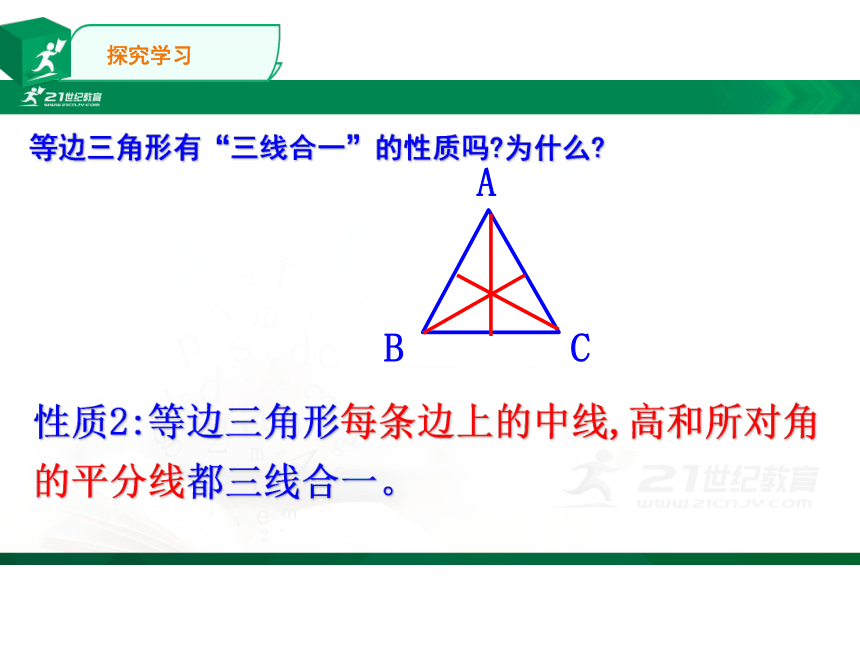
等边三角形有“三线合一”的性质吗 为什么
性质2:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探究学习
3、等边三角形是轴对称图形吗 有几条对称轴
探究学习
等边三角形的性质3
2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等
探究学习
一个三角形满足什么条件就是等边三角形
活动2:探究等边三角形的判定
探究学习
1.在△ABC中,∠A=∠B=∠C,你能得到 AB=BC=CA吗?为什么?
2.在△ABC中,AB=BC,∠A=60 ° ( ∠B=60°或 ∠C =60°)你能得到AB=BC=CA吗?为什么?
大胆猜想
A
B
C
三个角都相等的三角形是等边三角形。
已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
几何语言:
∵ ∠A= ∠ B=∠C
∴ AB=AC=BC(或△ABC是等边三角形)
判定1:
归纳猜想
有一个角是60。的等腰三角形是等边三角形
A
B
C
已知: AB=AC ∠A=60。
求证: AB=AC=BC
证明:
几何语言:
∵AB=AC ∠A= 60。
∴ AB=AC=BC
判定2:
归纳猜想
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边三角形.
等边三角形
等腰三角形
归纳猜想
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
定义 性质 判定
等 腰 三 角 形
等 边 三 角 形
有两条边相等
1、两个底角相等
2、三线合一
3、对称轴一条
1、三个角都相等
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有
一个角是600
对比学习
例.如图,在等边三角形ABC的边AB,AC
上分别截取AD=AE,△ADE是等边三角形吗?试说明理由。
A
B
C
D
E
你还有其它方法
使△ADE是等边三
角形吗?
例题精讲
解法一: ∵ △ABC为等边三角形
∴ ∠A=60 °
又∵AD=AE
∴ △ADE为等边三角形(判定2)
例题精讲
解法二: ∵ △ABC为等边三角形
∴∠A= 60 °
又∵AD=AE
即∠ ADE = ∠ AED = ∠A = 60 °
∴ △ADE为等边三角形(判定1)
例题精讲
1. 对于等边三角形,下列说法不成立的是( )
A.三条边都相等 B.每个角都是60°
C.有三条对称轴 D.两条高互相垂直
2.等腰三角形的腰长为2,顶角与底角相等,则这个等腰三角形的周长为( )
A.4 B.5 C.6 D.无法确定
3.若等腰三角形的腰长为2,顶角大于底角,则这个等腰三角形的周长为( )
A.6 B.大于6 C.小于6 D无法确定
、
练测促学
D
C
B
4.已知:
求证:AE=CD
练测促学
都是等边三角形.
证明:∵△ABC, △DBE是等边三角形
∴AB=BC, ∠ABE= ∠CBD,BE=BD
在△ABE与△CBD中
∠ABE= ∠CBD
AB=BC
BE=BD
∴ △ABE ≌ △CBD(SAS)
∴AE=CD
练测促学
如图,已知等边△ABC 中,BD=CE,AD与BE交于点P,求∠APE的度数.
拓展延伸
请你说一说这节课的收获和体验让大家与你一起分享 ?
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版 八年级上
13.3.2 等边三角形
1、我们是怎样研究等腰三角形的?
定义 性质 判定
性质:边 角 特殊线段 对称性
2、我们可以从哪些方面研究等边三角形呢?
3、一个三角形满足什么条件就是等边三角形?
对比学习
等腰三角形
等边三角形
一般
三角形
定义:三条边 都相等的三角形叫做等边三角形。
特殊的等腰三角形
一般三角形
等腰
三角形
等边三角形
底≠腰
底=腰
有两条边相等
{
(正三角形)
对比学习
小明假设等腰三角形底角为60°,得出了三个角都是60°,小亮假设顶角为60°,也得出了三个角都是60°,根据“等角对等边”,最后得出结论:三边都相等。
老师告诉他们“这种三条边都相等的叫做等边三角形”。小明、小亮也发表了自己的看法, 小明认为“三条边都相等的三角形是等边三角形,而不是等腰三角形”;小亮认为“等边三角形也还是等腰三角形,只是比一般的等腰三角形特殊而已”., 小明、小亮谁说的有道理呢?学完这节课就能见分晓。
情景导入
活动1: 探究等边三角形的性质
1.等边三角形边、角具有什么性质?
2.等边三角形有“三线合一”的性质吗 为什么
3.等边三角形是轴对称图形吗?有几条对称轴?
探究学习
等边三角形的三个内角都相等
并且每一个内角都等于60。
A
B
C
性质1:
等边三角形的内角都相等吗
探究学习
∵AB=AC=BC
∴∠A= ∠ B=∠C= 60。
几何语言:
已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60。
A
B
C
探究学习
等边三角形有“三线合一”的性质吗 为什么
性质2:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探究学习
3、等边三角形是轴对称图形吗 有几条对称轴
探究学习
等边三角形的性质3
2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.
4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等
探究学习
一个三角形满足什么条件就是等边三角形
活动2:探究等边三角形的判定
探究学习
1.在△ABC中,∠A=∠B=∠C,你能得到 AB=BC=CA吗?为什么?
2.在△ABC中,AB=BC,∠A=60 ° ( ∠B=60°或 ∠C =60°)你能得到AB=BC=CA吗?为什么?
大胆猜想
A
B
C
三个角都相等的三角形是等边三角形。
已知: ∠A= ∠ B=∠C
求证: AB=AC=BC
几何语言:
∵ ∠A= ∠ B=∠C
∴ AB=AC=BC(或△ABC是等边三角形)
判定1:
归纳猜想
有一个角是60。的等腰三角形是等边三角形
A
B
C
已知: AB=AC ∠A=60。
求证: AB=AC=BC
证明:
几何语言:
∵AB=AC ∠A= 60。
∴ AB=AC=BC
判定2:
归纳猜想
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边三角形.
等边三角形
等腰三角形
归纳猜想
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
定义 性质 判定
等 腰 三 角 形
等 边 三 角 形
有两条边相等
1、两个底角相等
2、三线合一
3、对称轴一条
1、三个角都相等
2、三线合一
3、对称轴三条
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有
一个角是600
对比学习
例.如图,在等边三角形ABC的边AB,AC
上分别截取AD=AE,△ADE是等边三角形吗?试说明理由。
A
B
C
D
E
你还有其它方法
使△ADE是等边三
角形吗?
例题精讲
解法一: ∵ △ABC为等边三角形
∴ ∠A=60 °
又∵AD=AE
∴ △ADE为等边三角形(判定2)
例题精讲
解法二: ∵ △ABC为等边三角形
∴∠A= 60 °
又∵AD=AE
即∠ ADE = ∠ AED = ∠A = 60 °
∴ △ADE为等边三角形(判定1)
例题精讲
1. 对于等边三角形,下列说法不成立的是( )
A.三条边都相等 B.每个角都是60°
C.有三条对称轴 D.两条高互相垂直
2.等腰三角形的腰长为2,顶角与底角相等,则这个等腰三角形的周长为( )
A.4 B.5 C.6 D.无法确定
3.若等腰三角形的腰长为2,顶角大于底角,则这个等腰三角形的周长为( )
A.6 B.大于6 C.小于6 D无法确定
、
练测促学
D
C
B
4.已知:
求证:AE=CD
练测促学
都是等边三角形.
证明:∵△ABC, △DBE是等边三角形
∴AB=BC, ∠ABE= ∠CBD,BE=BD
在△ABE与△CBD中
∠ABE= ∠CBD
AB=BC
BE=BD
∴ △ABE ≌ △CBD(SAS)
∴AE=CD
练测促学
如图,已知等边△ABC 中,BD=CE,AD与BE交于点P,求∠APE的度数.
拓展延伸
请你说一说这节课的收获和体验让大家与你一起分享 ?
课堂小结
https://www.21cnjy.com/help/help_extract.php
