2021—2022学年鲁教版(五四制)七年级数学上册_3.2 一定是直角三角形吗 课件(共30张PPT)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)七年级数学上册_3.2 一定是直角三角形吗 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 493.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
3.2 一定是直角三角形吗
第三章 勾股定理
复习勾股定理:
(1)直角三角形两直角边的平方和等于斜边的
平方,如果用a,b和c分别表示直角三角形的两
直角边和斜边,那么a2+b2=c2。
A
B
C
a
b
c
(2)符号语言:
∵ ∠C=90° (已知)
∴ a2+b2=c2 (勾股定理)
熟记
121
144
169
196
225
256
289
324
361
测:
1.求以5,12为直角边的直角三角形的斜边长;
2.求以3,4为两边的直角三角形的第三条边的平方。
找斜边
学习目标:
1.经历勾股定理的逆定理的探索过程,进
一步提高推理能力;
2.掌握勾股定理的逆定理,并能进行简单
应用;
3.了解勾股数的概念,并会识别一组勾股
数。
如果a2+b2=c2,那么这个三角形是直角三角形吗?
A
B
C
a
b
c
用a,b,c分别表示三角形的三边
提出问题:
做一做
下面的每组数分别是一个三角形的三边长a,b,c,而且都满足a2+b2=c2 :
① 3,4,5
② 5,12,13
③ 8,15,17
分别以每组数为三边作出三角形,用量角器
量一量,你有什么发现?
9+16=25
25+144=169
64+225=289
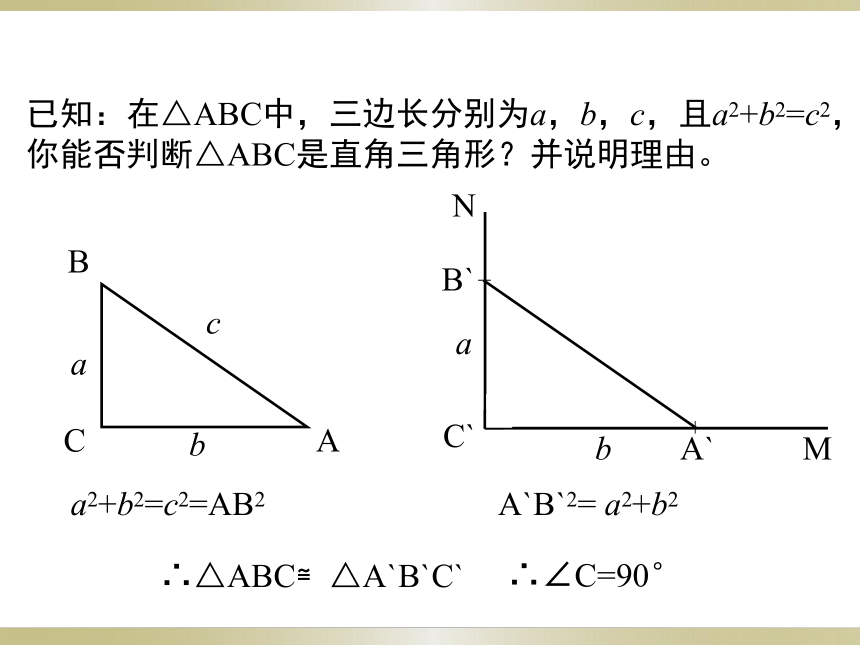
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2,你能否判断△ABC是直角三角形?并说明理由。
A
B
C
a
b
c
M
C`
N
A`
B`
a
b
a2+b2=c2=AB2
A`B`2= a2+b2
∴△ABC≌△A`B`C`
∴∠C=90°
新知归纳
“勾股定理”逆定理:
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
∵a2+b2=c2(已知)
(2)符号语言:
∴ ABC是直角三角形
(勾股定理逆定理)
∠C=90°(c是斜边)
拓广探索
下列几组数据能否作为直角三角形的三边?
(1) 9,12,15; (2) 15,36,39;
(3) 12,35,36 ; (4) 12,18,22。
(1) 92+122=152
能作为直角三角形的三边(15斜边)
(2) 152+362=392
能作为直角三角形的三边(39斜边)
(3) 122+352≠362
不能作为直角三角形的三边
(4) 122+182≠222
不能作为直角三角形的三边
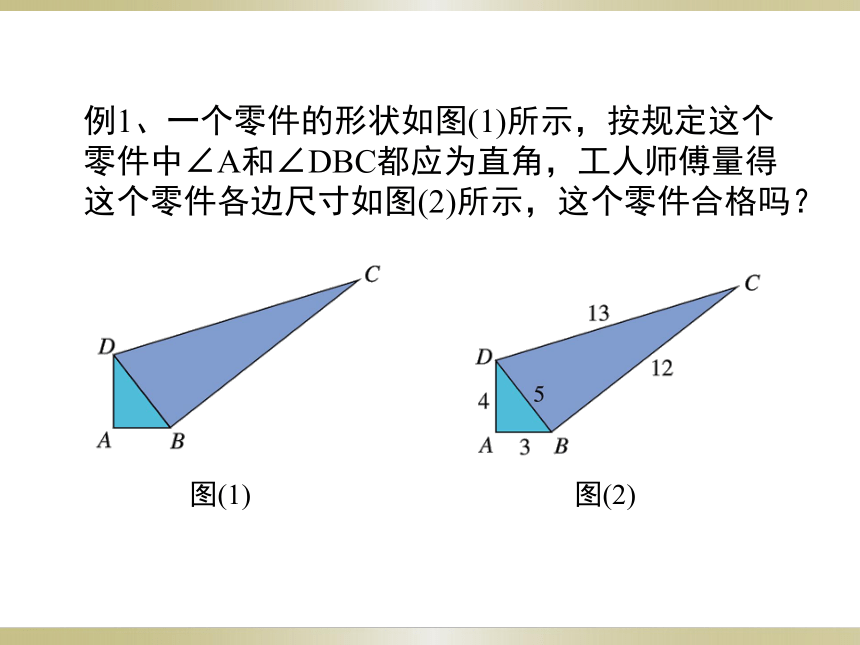
例1、一个零件的形状如图(1)所示,按规定这个
零件中∠A和∠DBC都应为直角,工人师傅量得
这个零件各边尺寸如图(2)所示,这个零件合格吗?
图(1)
图(2)
新知归纳
“勾股定理”逆定理的应用:
已知三边,判定直角三角形。
判定直角三角形的方法:
(1)角:有一个角(最大角)是直角的三角形是直角三角形;
(2)边:勾股定理逆定理
如果三角形的三边长a,b,c (a巩固练习:
判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=15°, ∠B=75 °
(2)在△ABC中,AC=12, AB=20,
BC=16
(3) △ABC的三边长a,b,c满足
判定钝角三角形的方法:
(1)角:有一个角(最大角)是钝角的三角形是钝角三角形;
(2)边:
如果三角形的三边长a,b,c(a判定锐角三角形的方法:
(1)角:三个角都是锐角(最大角是锐角)的三角形是锐角三角形;
(2)边:
如果三角形的三边长a,b,c(ac2,那么这个三角形是锐角三角形。
1、如图,在正方形ABCD中,AB=4,AE=2,
DF=1,图中有几个直角三角形,你是如何判断
的?与你的同伴交流。
4
2
2
1
3
4
BE2=42+22=20
FE2=12+22=5
FB2=32+42=25
BE2+FE2=FB2
巩固练习:
2、如图,哪些是直角三角形,哪些不是,说说
你的理由?
92+122=152
问题一:以上两组数叫勾股数,讨论一下勾股数有什么特点?
152+362=392
1、都是正整数;
(1) 9,12,15; (2) 15,36,39;
2、都满足a2+b2=c2。
新知归纳
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
跟踪练习:
在下列各组数据中,是勾股数的一组
是( )
A.0.3 0.4 0.5 B.6 8 10
C.4 5 6 D.
E.1.4 4.8 5 F.-15 36 39
常用勾股数:
3, 4, 5
5, 12, 13
7, 24, 25
9, 40, 41
11,60,61
…
6, 8, 10
8, 15, 17
10, 24, 26
12, 35, 37
14, 48, 50
…
同学们,大家能找到这些勾股数的规律吗?
课后讨论一下
问题二:
(1) 9,12,15; (2) 15,36,39;
这两组勾股数都不是最简数?提出公因式你有什么发现?
所以:
若a,b,c是一组勾股数,则na,nb,nc(n是任意正整数)也是一组勾股数。
(1)下表中第一列每组数都是勾股数,补全下表,这些数的2倍、3倍、4倍、10倍还是勾股数吗?任意倍呢?说说你的理由。
(2)如果将直角三角形的三边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?
1.已知三角形的三边长分别是
(m为大于1的自然数),试判断这个三角形的形状。
判断三角形形状的步骤:
(1)比较三角形三边的长度,并找出最长边;
(2)验证最长边的平方和与另外两边的平方和的关系,若相等,则为直角三角形,否则钝角或锐角三角形。
练习:
2.如图,在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°
求∠DAB的度数。
A
B
C
D
“勾股定理”逆定理的应用:
已知三边,判定直角三角形。
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
本节课总结:
课堂小测:
判断 ABC的形状,说明理由(网格边为1)
3.2 一定是直角三角形吗
第三章 勾股定理
复习勾股定理:
(1)直角三角形两直角边的平方和等于斜边的
平方,如果用a,b和c分别表示直角三角形的两
直角边和斜边,那么a2+b2=c2。
A
B
C
a
b
c
(2)符号语言:
∵ ∠C=90° (已知)
∴ a2+b2=c2 (勾股定理)
熟记
121
144
169
196
225
256
289
324
361
测:
1.求以5,12为直角边的直角三角形的斜边长;
2.求以3,4为两边的直角三角形的第三条边的平方。
找斜边
学习目标:
1.经历勾股定理的逆定理的探索过程,进
一步提高推理能力;
2.掌握勾股定理的逆定理,并能进行简单
应用;
3.了解勾股数的概念,并会识别一组勾股
数。
如果a2+b2=c2,那么这个三角形是直角三角形吗?
A
B
C
a
b
c
用a,b,c分别表示三角形的三边
提出问题:
做一做
下面的每组数分别是一个三角形的三边长a,b,c,而且都满足a2+b2=c2 :
① 3,4,5
② 5,12,13
③ 8,15,17
分别以每组数为三边作出三角形,用量角器
量一量,你有什么发现?
9+16=25
25+144=169
64+225=289
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2,你能否判断△ABC是直角三角形?并说明理由。
A
B
C
a
b
c
M
C`
N
A`
B`
a
b
a2+b2=c2=AB2
A`B`2= a2+b2
∴△ABC≌△A`B`C`
∴∠C=90°
新知归纳
“勾股定理”逆定理:
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
∵a2+b2=c2(已知)
(2)符号语言:
∴ ABC是直角三角形
(勾股定理逆定理)
∠C=90°(c是斜边)
拓广探索
下列几组数据能否作为直角三角形的三边?
(1) 9,12,15; (2) 15,36,39;
(3) 12,35,36 ; (4) 12,18,22。
(1) 92+122=152
能作为直角三角形的三边(15斜边)
(2) 152+362=392
能作为直角三角形的三边(39斜边)
(3) 122+352≠362
不能作为直角三角形的三边
(4) 122+182≠222
不能作为直角三角形的三边
例1、一个零件的形状如图(1)所示,按规定这个
零件中∠A和∠DBC都应为直角,工人师傅量得
这个零件各边尺寸如图(2)所示,这个零件合格吗?
图(1)
图(2)
新知归纳
“勾股定理”逆定理的应用:
已知三边,判定直角三角形。
判定直角三角形的方法:
(1)角:有一个角(最大角)是直角的三角形是直角三角形;
(2)边:勾股定理逆定理
如果三角形的三边长a,b,c (a
判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=15°, ∠B=75 °
(2)在△ABC中,AC=12, AB=20,
BC=16
(3) △ABC的三边长a,b,c满足
判定钝角三角形的方法:
(1)角:有一个角(最大角)是钝角的三角形是钝角三角形;
(2)边:
如果三角形的三边长a,b,c(a
(1)角:三个角都是锐角(最大角是锐角)的三角形是锐角三角形;
(2)边:
如果三角形的三边长a,b,c(a
1、如图,在正方形ABCD中,AB=4,AE=2,
DF=1,图中有几个直角三角形,你是如何判断
的?与你的同伴交流。
4
2
2
1
3
4
BE2=42+22=20
FE2=12+22=5
FB2=32+42=25
BE2+FE2=FB2
巩固练习:
2、如图,哪些是直角三角形,哪些不是,说说
你的理由?
92+122=152
问题一:以上两组数叫勾股数,讨论一下勾股数有什么特点?
152+362=392
1、都是正整数;
(1) 9,12,15; (2) 15,36,39;
2、都满足a2+b2=c2。
新知归纳
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
跟踪练习:
在下列各组数据中,是勾股数的一组
是( )
A.0.3 0.4 0.5 B.6 8 10
C.4 5 6 D.
E.1.4 4.8 5 F.-15 36 39
常用勾股数:
3, 4, 5
5, 12, 13
7, 24, 25
9, 40, 41
11,60,61
…
6, 8, 10
8, 15, 17
10, 24, 26
12, 35, 37
14, 48, 50
…
同学们,大家能找到这些勾股数的规律吗?
课后讨论一下
问题二:
(1) 9,12,15; (2) 15,36,39;
这两组勾股数都不是最简数?提出公因式你有什么发现?
所以:
若a,b,c是一组勾股数,则na,nb,nc(n是任意正整数)也是一组勾股数。
(1)下表中第一列每组数都是勾股数,补全下表,这些数的2倍、3倍、4倍、10倍还是勾股数吗?任意倍呢?说说你的理由。
(2)如果将直角三角形的三边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?
1.已知三角形的三边长分别是
(m为大于1的自然数),试判断这个三角形的形状。
判断三角形形状的步骤:
(1)比较三角形三边的长度,并找出最长边;
(2)验证最长边的平方和与另外两边的平方和的关系,若相等,则为直角三角形,否则钝角或锐角三角形。
练习:
2.如图,在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°
求∠DAB的度数。
A
B
C
D
“勾股定理”逆定理的应用:
已知三边,判定直角三角形。
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
本节课总结:
课堂小测:
判断 ABC的形状,说明理由(网格边为1)
