冀教版九年级数学下册31.1 确定事件和随机事件课件(35张ppt)
文档属性
| 名称 | 冀教版九年级数学下册31.1 确定事件和随机事件课件(35张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 955.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
31.1 确定事件和随机事件
第三十一章 随机事件的概率
课时导入
2010年11月23日 晴
早上,我晚起了。于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿。我想我真不走运,她经常在办公室的啊。今天真倒霉!我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任。
中午放学回家,我看了一场篮球赛。我想长大后会比姚明还高,我将长到3米高。看完比赛后,我又回到学校上学。
下午放学后,我开始写作业。今天作业太多了,我不停的写啊,一直写到太阳从西边落下。
请问:画横线部分的事情一定会发生吗?
回顾与思考
知识点
确定事件
知1-讲
感悟新知
1
A盒中有10个大小和质地都相同的红球,搅匀后从中任意摸出1个球. 事先能肯定摸到的是红球吗 能摸到黄球吗
问 题
知1-讲
感悟新知
摸到红球
必然发生
必然不会发生
摸到黄球
知1-讲
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
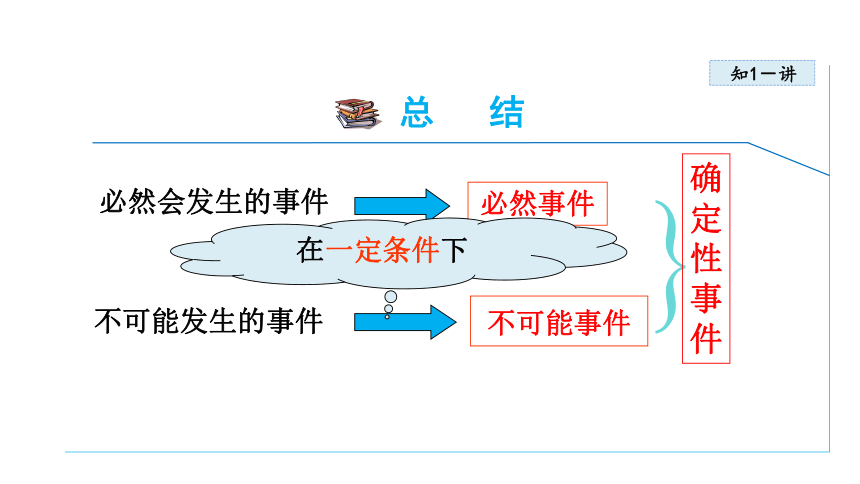
在一定条件下,必然发生的事情叫做必然事件,不可能发生的事情叫做不可能事件,必然事件和不可能事件统称为确定事件.
知1-讲
感悟新知
特别提醒:
1.确定性事件在事件发生前是可以预知结果的,随机事件在事件发生前是不能预知结果的,随机事件也称为“偶然性事件”.
2. 按事件的确定性划分,事件可划分为确定事件和不确定事件(即随机事件).
3. 一般地,描述已被确定的真理或者客观存在的事实的事件是必然事件;描述违背已被确定的真理或者违背客观存在的事实的事件是不可能事件.
知1-练
感悟新知
1.想一想:5名同学参加演讲比赛,以抽签方式决定每
个人的出场顺序。签筒中有5张形
状大小、完全相同的纸签,上面
分别标有出场的序号1、2、3、
4、5,小军首先抽签,他在
看不到纸签上数字的情况
下从筒中随机(任意)地
取一张纸签,请考虑以下问题:
形状大小相同的签
知1-练
感悟新知
(1)抽到的序号有几种可能的结果?
(2)抽到的序号小于6吗?
(3)抽到的序号会是0吗?
1、2、3、4、5.
一定是.
不可能.
知1-练
感悟新知
2、投掷一个质地均匀的正方体骰子.骰子六个面上分
别刻有1到6的点数.每组同学掷10次并记录结果,
并完成以下练习.
在(2)(3)(4)三种结果中哪些是必然发生的?哪些是
不可能发生的?
知1-练
感悟新知
(3)出现的点数是7.
(1)可能出现哪些点数?
(1、2、3、4、5、6)
(必然发生)
(不可能发生)
(2)出现的点数大于0.
不可能事件
必然事件
知1-讲
总 结
感悟新知
必然会发生的事件
必然事件
不可能发生的事件
不可能事件
在一定条件下
确定性事件
感悟新知
知1-练
例 1
同时抛掷两枚质地均匀的正方体骰子,在下列事件中,哪些是必然事件?哪些是不可能事件?并指出哪些是确定事件.
A.两枚骰子上的点数之和是8;
B.两枚骰子上的点数之和在2~12(包括2和12)范围内;
C.两枚骰子上的点数之和是1;
D.两枚骰子上的点数之和是13;
E.两枚骰子上的点数一个是奇数一个是偶数.
感悟新知
知1-练
每枚骰子上的点数分别为1,2,3,4,5,6,那么同
时抛掷两枚骰子,上面的两个点数之和在2~12(包括2和12)范围内,其中最小的是2,最大的是12. A的结果不确定,故不是确定事件,B一定会发生,故是必然事件,C是不可能发生的,所以是不可能事件,D是不可能发生的,所以是不可能事件,E的结果不确定.
B是必然事件;C,D是不可能事件;B,C,D都属于确
定事件.
解:
导引:
感悟新知
知1-练
下列事件中,是必然事件的为( )
A.3天内会下雨
B.打开电视机,正在播放广告
C.367人中至少有2人公历生日相同
D.某妇产医院里,下一个出生的婴儿是女孩
1.
C
感悟新知
知1-练
下列事件是必然事件的是( )
A.某种彩票中奖率是1%,则买这种彩票100张
一定会中奖
B.一组数据1,2,4,5的平均数是4
C.三角形的内角和等于180°
D.若a是实数,则|a|>0
2.
C
感悟新知
知1-练
不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A.摸出的是3个白球
B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球
D.摸出的是2个黑球、1个白球
3.
A
感悟新知
知1-练
下列事件:①在足球赛中,弱队战胜强队;②抛掷1枚硬币,硬币落地时正面朝上;③任取两个正整数,其和大于1;④长为3 cm,5 cm,9 cm的三条线段能围成一个三角形.其中,必然事件有( )
A.1个 B.2个
C.3个 D.4个
4.
A
知识点
随机事件
知2-讲
感悟新知
2
活动:盒子中装有4个黄球2个白球,这些球形状、大 小、质地等完全相同,在看不到球的条件下,随机地 从袋子中摸出一个球. 你想一下: 究竟摸出的这个球是白球还是黄球?
可能是白球,也有可能是黄球.
随机事件
知2-讲
感悟新知
随机事件:在一定条件下,有些事件可能发生也
可能不发生,这样的事件称为随机事件或不确定
性事件.
随机事件
知2-练
感悟新知
例2
在一个不透明的口袋中装有大小、外形完全相同的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了,请判断以下事件是随机事件、不可能事件、还是必然事件.
(1)从口袋中一次任意取出一个球,是白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任取5个球,只有蓝球和白球,没有红球;
(4)从口袋中一次任意取出6个球,恰好红、蓝、白三种颜
色的球都齐了.
随机事件
知2-练
感悟新知
(1)口袋中有红球、蓝球、白球,任意取出一个球,三
种颜色的球都有可能,所以是随机事件;
(2)因为口袋中一共有3个蓝球,所以一次任取5个球,
一定不可能全是蓝球,所以是不可能事件;
(3)从口袋中一次任取5个球,有可能有红球也有可能没
有红球,结果是不确定的,故是随机事件;
(4)从口袋中一次任意取出6个球,可能是红球和蓝球两
种或红球和白球两种,也有可能是三种颜色的球都
有,故结果是不确定的,所以是随机事件.
导引:
随机事件
知2-练
感悟新知
(1)可能发生,也可能不发生,是随机事件;
(2)一定不会发生,是不可能事件;
(3)可能发生,也可能不发生,是随机事件;
(4)可能发生,也可能不发生,是随机事件.
解:
随机事件
知2-练
感悟新知
指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)在标准大气压下,水在100 ℃时沸腾.
(2)向空中抛掷一个玻璃球,球落到地面.
(3)在没有氧气的密闭瓶子中,蜡烛能燃烧.
(4)解答有4个选项的单项选择题,随意猜一个答
案,猜中正确答案.
(5)某射击运动员射击一次,成绩为10环.
1.
随机事件
知2-练
感悟新知
(1)必然事件;
(2)必然事件;
(3)不可能事件;
(4)随机事件;
(5)随机事件.
解:
随机事件
知2-练
感悟新知
请你再举出几个随机事件的例子.
2.
明天会下雨;
掷一颗骰子,点数为5的面朝上.
(答案不唯一)
解:
知2-练
感悟新知
“a是实数,|a|≥0”这一事件是( )
A.必然事件
B.不确定事件
C.不可能事件
D.随机事件
3.
A
知2-练
感悟新知
射击运动员射击一次,命中靶心”这个事件是( )
A.确定事件
B.必然事件
C.不可能事件
D.不确定事件
4.
D
知2-练
感悟新知
下列事件中,属于随机事件的是( )
A. 的值比8大
B.购买一张彩票,中奖
C.地球自转的同时也在绕日公转
D.袋中只有5个黄球,摸出一个球是白球
5.
B
知2-练
感悟新知
下列说法正确的是( )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随 机事件
D.“经过有交通信号灯的路口 ,遇到红灯”是必然事件
6.
C
知2-练
感悟新知
下列成语所描述的事件是必然事件的是( )
A.瓮中捉鳖
B.拔苗助长
C.守株待兔
D.水中捞月
7.
A
知2-练
感悟新知
下列说法中不正确的是( )
A.“某篮球运动员罚篮一次,正好命中”属于随机事件
B.“13名同学中至少有两名同学的出生月份相同” 属
于必然事件
C.“在标准大气压下,当温度降到-1 ℃时,水结成冰”
属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是
白球”属于不可能事件
8.
C
课堂小结
确定事件和随机事件
事
件
确定性事件
随机事件(可能会发生)
必然事件(一定会发生)
不可能事件(不可能会发生)
课堂小结
事件“任意写出一个实数,这个实数的平方是正数”是( )
A.必然事件 B.不可能事件
C.随机事件 D.大部分情况下是必然事件
C
确定事件和随机事件
课堂小结
诊断:错解的原因有两种:①对实数的概念不理解:当这个
实数不为0时,其平方是正数;当这个实数为0时,其
平方仍是0.所以该事件是随机事件.②对事件分类的
概念不理解:每个事件一定是必然事件、不可能事
件、随机事件中的一种,没有第四种事件.
确定事件和随机事件
课堂小结
易错点:对事件分类的概念不理解而导致错解.
确定事件和随机事件
31.1 确定事件和随机事件
第三十一章 随机事件的概率
课时导入
2010年11月23日 晴
早上,我晚起了。于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿。我想我真不走运,她经常在办公室的啊。今天真倒霉!我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任。
中午放学回家,我看了一场篮球赛。我想长大后会比姚明还高,我将长到3米高。看完比赛后,我又回到学校上学。
下午放学后,我开始写作业。今天作业太多了,我不停的写啊,一直写到太阳从西边落下。
请问:画横线部分的事情一定会发生吗?
回顾与思考
知识点
确定事件
知1-讲
感悟新知
1
A盒中有10个大小和质地都相同的红球,搅匀后从中任意摸出1个球. 事先能肯定摸到的是红球吗 能摸到黄球吗
问 题
知1-讲
感悟新知
摸到红球
必然发生
必然不会发生
摸到黄球
知1-讲
感悟新知
符号“ ”读作“等价于”,
它表示从符“ ”的左
端可以推出右端,从右
端也可以推出左端.
在一定条件下,必然发生的事情叫做必然事件,不可能发生的事情叫做不可能事件,必然事件和不可能事件统称为确定事件.
知1-讲
感悟新知
特别提醒:
1.确定性事件在事件发生前是可以预知结果的,随机事件在事件发生前是不能预知结果的,随机事件也称为“偶然性事件”.
2. 按事件的确定性划分,事件可划分为确定事件和不确定事件(即随机事件).
3. 一般地,描述已被确定的真理或者客观存在的事实的事件是必然事件;描述违背已被确定的真理或者违背客观存在的事实的事件是不可能事件.
知1-练
感悟新知
1.想一想:5名同学参加演讲比赛,以抽签方式决定每
个人的出场顺序。签筒中有5张形
状大小、完全相同的纸签,上面
分别标有出场的序号1、2、3、
4、5,小军首先抽签,他在
看不到纸签上数字的情况
下从筒中随机(任意)地
取一张纸签,请考虑以下问题:
形状大小相同的签
知1-练
感悟新知
(1)抽到的序号有几种可能的结果?
(2)抽到的序号小于6吗?
(3)抽到的序号会是0吗?
1、2、3、4、5.
一定是.
不可能.
知1-练
感悟新知
2、投掷一个质地均匀的正方体骰子.骰子六个面上分
别刻有1到6的点数.每组同学掷10次并记录结果,
并完成以下练习.
在(2)(3)(4)三种结果中哪些是必然发生的?哪些是
不可能发生的?
知1-练
感悟新知
(3)出现的点数是7.
(1)可能出现哪些点数?
(1、2、3、4、5、6)
(必然发生)
(不可能发生)
(2)出现的点数大于0.
不可能事件
必然事件
知1-讲
总 结
感悟新知
必然会发生的事件
必然事件
不可能发生的事件
不可能事件
在一定条件下
确定性事件
感悟新知
知1-练
例 1
同时抛掷两枚质地均匀的正方体骰子,在下列事件中,哪些是必然事件?哪些是不可能事件?并指出哪些是确定事件.
A.两枚骰子上的点数之和是8;
B.两枚骰子上的点数之和在2~12(包括2和12)范围内;
C.两枚骰子上的点数之和是1;
D.两枚骰子上的点数之和是13;
E.两枚骰子上的点数一个是奇数一个是偶数.
感悟新知
知1-练
每枚骰子上的点数分别为1,2,3,4,5,6,那么同
时抛掷两枚骰子,上面的两个点数之和在2~12(包括2和12)范围内,其中最小的是2,最大的是12. A的结果不确定,故不是确定事件,B一定会发生,故是必然事件,C是不可能发生的,所以是不可能事件,D是不可能发生的,所以是不可能事件,E的结果不确定.
B是必然事件;C,D是不可能事件;B,C,D都属于确
定事件.
解:
导引:
感悟新知
知1-练
下列事件中,是必然事件的为( )
A.3天内会下雨
B.打开电视机,正在播放广告
C.367人中至少有2人公历生日相同
D.某妇产医院里,下一个出生的婴儿是女孩
1.
C
感悟新知
知1-练
下列事件是必然事件的是( )
A.某种彩票中奖率是1%,则买这种彩票100张
一定会中奖
B.一组数据1,2,4,5的平均数是4
C.三角形的内角和等于180°
D.若a是实数,则|a|>0
2.
C
感悟新知
知1-练
不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A.摸出的是3个白球
B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球
D.摸出的是2个黑球、1个白球
3.
A
感悟新知
知1-练
下列事件:①在足球赛中,弱队战胜强队;②抛掷1枚硬币,硬币落地时正面朝上;③任取两个正整数,其和大于1;④长为3 cm,5 cm,9 cm的三条线段能围成一个三角形.其中,必然事件有( )
A.1个 B.2个
C.3个 D.4个
4.
A
知识点
随机事件
知2-讲
感悟新知
2
活动:盒子中装有4个黄球2个白球,这些球形状、大 小、质地等完全相同,在看不到球的条件下,随机地 从袋子中摸出一个球. 你想一下: 究竟摸出的这个球是白球还是黄球?
可能是白球,也有可能是黄球.
随机事件
知2-讲
感悟新知
随机事件:在一定条件下,有些事件可能发生也
可能不发生,这样的事件称为随机事件或不确定
性事件.
随机事件
知2-练
感悟新知
例2
在一个不透明的口袋中装有大小、外形完全相同的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了,请判断以下事件是随机事件、不可能事件、还是必然事件.
(1)从口袋中一次任意取出一个球,是白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任取5个球,只有蓝球和白球,没有红球;
(4)从口袋中一次任意取出6个球,恰好红、蓝、白三种颜
色的球都齐了.
随机事件
知2-练
感悟新知
(1)口袋中有红球、蓝球、白球,任意取出一个球,三
种颜色的球都有可能,所以是随机事件;
(2)因为口袋中一共有3个蓝球,所以一次任取5个球,
一定不可能全是蓝球,所以是不可能事件;
(3)从口袋中一次任取5个球,有可能有红球也有可能没
有红球,结果是不确定的,故是随机事件;
(4)从口袋中一次任意取出6个球,可能是红球和蓝球两
种或红球和白球两种,也有可能是三种颜色的球都
有,故结果是不确定的,所以是随机事件.
导引:
随机事件
知2-练
感悟新知
(1)可能发生,也可能不发生,是随机事件;
(2)一定不会发生,是不可能事件;
(3)可能发生,也可能不发生,是随机事件;
(4)可能发生,也可能不发生,是随机事件.
解:
随机事件
知2-练
感悟新知
指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)在标准大气压下,水在100 ℃时沸腾.
(2)向空中抛掷一个玻璃球,球落到地面.
(3)在没有氧气的密闭瓶子中,蜡烛能燃烧.
(4)解答有4个选项的单项选择题,随意猜一个答
案,猜中正确答案.
(5)某射击运动员射击一次,成绩为10环.
1.
随机事件
知2-练
感悟新知
(1)必然事件;
(2)必然事件;
(3)不可能事件;
(4)随机事件;
(5)随机事件.
解:
随机事件
知2-练
感悟新知
请你再举出几个随机事件的例子.
2.
明天会下雨;
掷一颗骰子,点数为5的面朝上.
(答案不唯一)
解:
知2-练
感悟新知
“a是实数,|a|≥0”这一事件是( )
A.必然事件
B.不确定事件
C.不可能事件
D.随机事件
3.
A
知2-练
感悟新知
射击运动员射击一次,命中靶心”这个事件是( )
A.确定事件
B.必然事件
C.不可能事件
D.不确定事件
4.
D
知2-练
感悟新知
下列事件中,属于随机事件的是( )
A. 的值比8大
B.购买一张彩票,中奖
C.地球自转的同时也在绕日公转
D.袋中只有5个黄球,摸出一个球是白球
5.
B
知2-练
感悟新知
下列说法正确的是( )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随 机事件
D.“经过有交通信号灯的路口 ,遇到红灯”是必然事件
6.
C
知2-练
感悟新知
下列成语所描述的事件是必然事件的是( )
A.瓮中捉鳖
B.拔苗助长
C.守株待兔
D.水中捞月
7.
A
知2-练
感悟新知
下列说法中不正确的是( )
A.“某篮球运动员罚篮一次,正好命中”属于随机事件
B.“13名同学中至少有两名同学的出生月份相同” 属
于必然事件
C.“在标准大气压下,当温度降到-1 ℃时,水结成冰”
属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是
白球”属于不可能事件
8.
C
课堂小结
确定事件和随机事件
事
件
确定性事件
随机事件(可能会发生)
必然事件(一定会发生)
不可能事件(不可能会发生)
课堂小结
事件“任意写出一个实数,这个实数的平方是正数”是( )
A.必然事件 B.不可能事件
C.随机事件 D.大部分情况下是必然事件
C
确定事件和随机事件
课堂小结
诊断:错解的原因有两种:①对实数的概念不理解:当这个
实数不为0时,其平方是正数;当这个实数为0时,其
平方仍是0.所以该事件是随机事件.②对事件分类的
概念不理解:每个事件一定是必然事件、不可能事
件、随机事件中的一种,没有第四种事件.
确定事件和随机事件
课堂小结
易错点:对事件分类的概念不理解而导致错解.
确定事件和随机事件
