冀教版数学九年级下册32.2.2由三视图到几何体课件(26张ppt)
文档属性
| 名称 | 冀教版数学九年级下册32.2.2由三视图到几何体课件(26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 09:10:48 | ||
图片预览






文档简介
(共26张PPT)
32.2 视图
第三十二章 投影与视图
课时导入
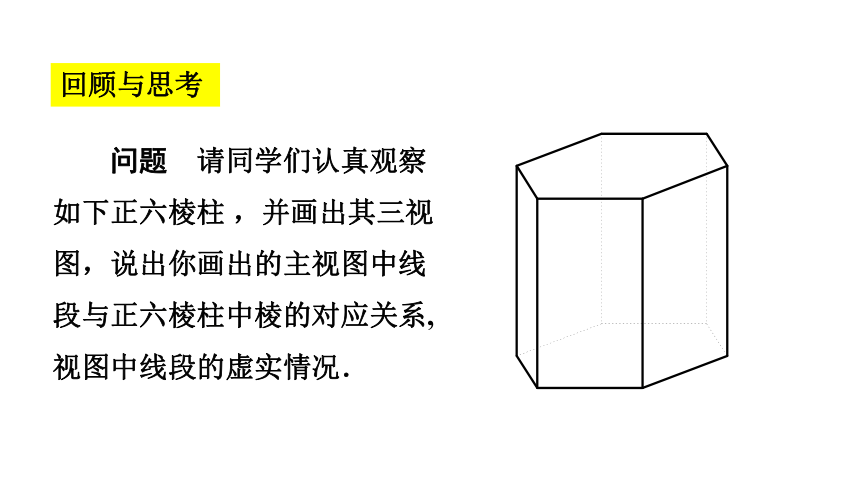
回顾与思考
问题 请同学们认真观察如下正六棱柱 ,并画出其三视图,说出你画出的主视图中线段与正六棱柱中棱的对应关系,视图中线段的虚实情况.
知识点
由三视图想象几何体
知1-讲
感悟新知
1
一个视图不能确定物体的空间形状,要根据三视
图描述几何体或实物原型时,必须将各视图对照起来
看. 根据主视图、俯视图和左视图想象立体图形的前后
面、上下面和左右面,然后再综合起来考虑整体图形.
知1-讲
感悟新知
由三视图想象几何体:
(1)方法:由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上面
和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径
进行分析.
知1-讲
感悟新知
特别提醒: 几何体、三视图和展开图之间的关系
1. 几何体的三视图和展开图都是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形,即三者之间可以互相转化.
2. 对于稍复杂的视图,可先将其化成几个简单的图形,再综合分析.
3. 一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等.
知1-练
感悟新知
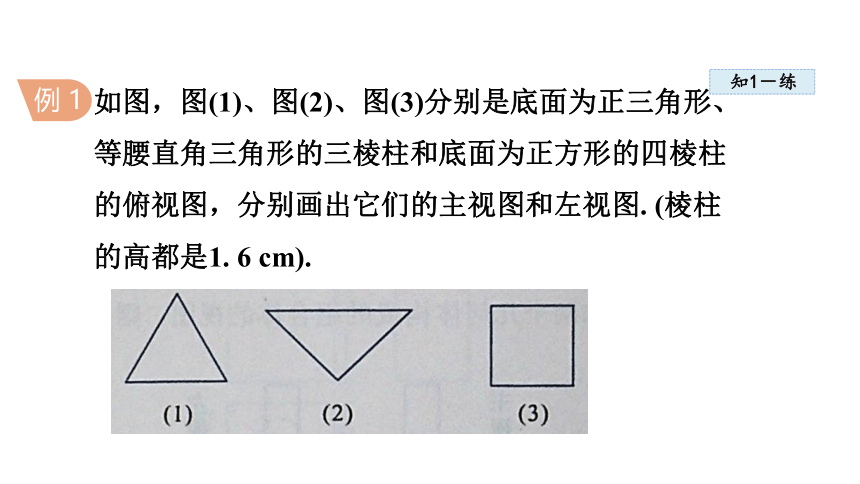
例 1
如图,图(1)、图(2)、图(3)分别是底面为正三角形、等腰直角三角形的三棱柱和底面为正方形的四棱柱的俯视图,分别画出它们的主视图和左视图. (棱柱的高都是1. 6 cm).
知1-练
感悟新知
如图所示.
解:
知1-讲
总 结
感悟新知
根据物体的三视图想象物体的形状,一般是由
俯视图确定物体在平面上的形状,根据左视图、主
视图想象出它在空间里的形状,从而确定物体的物
状.
知1-练
感悟新知
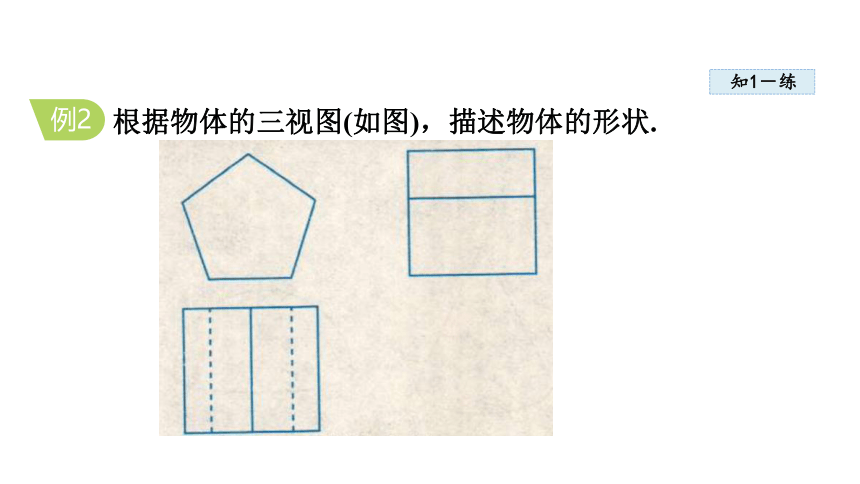
例2
根据物体的三视图(如图),描述物体的形状.
知1-练
感悟新知
由主视图可知,物体正面是正五边形; 由俯视图可
知,由上向下看到物体有两个面的视图 是矩形,
它们的交线是一条棱(中间的实线表示), 可见
到,另有两条棱(虚线表示)被遮挡;由左视 图
可知,物体左侧有两个面的视图是矩形,它们的
交线是一条棱(中间的实线表示),可见到.综合
各视图可知,物体的形状是正五棱柱.
分析:
知1-练
感悟新知
物体是正五棱柱形状的,如图所示.
解:
知1-练
感悟新知
1.
请根据下面两组几何体的视图,分別描述它们各是什么几何体?
(1)是圆锥;(2)是球.
解:
知1-练
感悟新知
2.
如图所示.
解:
根据下面的视图,画出几何体的草图.
知1-练
感悟新知
3.
这两个几何体分别是底面是正方形的四棱柱和圆柱.
解:
如图,已知两个几何体构成的组合体的视图, 则这两个几何体分别是哪种几何体?
知1-练
感悟新知
4.
如图是某个几何体的三视图,则该几何体是( )
A.圆锥
B.三棱柱
C.圆柱
D.三棱锥
B
知1-练
感悟新知
5.
如图中三视图对应的几何体是( )
C
知1-练
感悟新知
如图是一个几何体的三视图,描述其结构特征,最准确的是( )
A.底面是正六边形
B.底面是六边形,侧面是等腰梯形的棱台
C.上、下底面是正六边形,侧面是等腰梯形的棱台
D.底面是正六边形,侧面是等腰三角形的棱锥
C
6.
知1-练
感悟新知
7.
如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
A
知1-练
感悟新知
8.
一个几何体的三视图如图所示,该几何体是( )
D
知识点
由三视图确定组合体的数据
知2-讲
感悟新知
2
例 3
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状是图中的( )
D
知2-练
感悟新知
俯视图中,第一列最高有3个小立方块,第二列最高有2个小立方块,第三列最高有3个小立方块,因此,主视图从左到右可看到的小立方块个数依次为3、2、3,故选D.
导引:
知2-讲
总 结
感悟新知
由一种视图猜想另一种视图,中间也是跳跃一
步——还原几何体.先还原几何体,再确定另一种
视图.
随机事件
知2-练
感悟新知
1.
由若干个相同的小正方体组合而成的一个几何体
的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.3
B.4
C.5
D.6
C
知2-练
感悟新知
2.
一张桌子上摆放有若干个大小、形状完全相同的
碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
B
随机事件
知2-练
感悟新知
3.
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
A.
B.7
C.9
D.10
B
课堂小结
由三视图到几何体
1.通过这节课的学习,你有哪些收获?
2.由立体图形的三视图想象立体图形的形状时,你
有什么好的看法?与同伴交流一下.
32.2 视图
第三十二章 投影与视图
课时导入
回顾与思考
问题 请同学们认真观察如下正六棱柱 ,并画出其三视图,说出你画出的主视图中线段与正六棱柱中棱的对应关系,视图中线段的虚实情况.
知识点
由三视图想象几何体
知1-讲
感悟新知
1
一个视图不能确定物体的空间形状,要根据三视
图描述几何体或实物原型时,必须将各视图对照起来
看. 根据主视图、俯视图和左视图想象立体图形的前后
面、上下面和左右面,然后再综合起来考虑整体图形.
知1-讲
感悟新知
由三视图想象几何体:
(1)方法:由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上面
和左侧面,然后再综合起来考虑整体图形.
(2)过程:由三视图想象几何体形状,可通过以下途径
进行分析.
知1-讲
感悟新知
特别提醒: 几何体、三视图和展开图之间的关系
1. 几何体的三视图和展开图都是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形,即三者之间可以互相转化.
2. 对于稍复杂的视图,可先将其化成几个简单的图形,再综合分析.
3. 一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等.
知1-练
感悟新知
例 1
如图,图(1)、图(2)、图(3)分别是底面为正三角形、等腰直角三角形的三棱柱和底面为正方形的四棱柱的俯视图,分别画出它们的主视图和左视图. (棱柱的高都是1. 6 cm).
知1-练
感悟新知
如图所示.
解:
知1-讲
总 结
感悟新知
根据物体的三视图想象物体的形状,一般是由
俯视图确定物体在平面上的形状,根据左视图、主
视图想象出它在空间里的形状,从而确定物体的物
状.
知1-练
感悟新知
例2
根据物体的三视图(如图),描述物体的形状.
知1-练
感悟新知
由主视图可知,物体正面是正五边形; 由俯视图可
知,由上向下看到物体有两个面的视图 是矩形,
它们的交线是一条棱(中间的实线表示), 可见
到,另有两条棱(虚线表示)被遮挡;由左视 图
可知,物体左侧有两个面的视图是矩形,它们的
交线是一条棱(中间的实线表示),可见到.综合
各视图可知,物体的形状是正五棱柱.
分析:
知1-练
感悟新知
物体是正五棱柱形状的,如图所示.
解:
知1-练
感悟新知
1.
请根据下面两组几何体的视图,分別描述它们各是什么几何体?
(1)是圆锥;(2)是球.
解:
知1-练
感悟新知
2.
如图所示.
解:
根据下面的视图,画出几何体的草图.
知1-练
感悟新知
3.
这两个几何体分别是底面是正方形的四棱柱和圆柱.
解:
如图,已知两个几何体构成的组合体的视图, 则这两个几何体分别是哪种几何体?
知1-练
感悟新知
4.
如图是某个几何体的三视图,则该几何体是( )
A.圆锥
B.三棱柱
C.圆柱
D.三棱锥
B
知1-练
感悟新知
5.
如图中三视图对应的几何体是( )
C
知1-练
感悟新知
如图是一个几何体的三视图,描述其结构特征,最准确的是( )
A.底面是正六边形
B.底面是六边形,侧面是等腰梯形的棱台
C.上、下底面是正六边形,侧面是等腰梯形的棱台
D.底面是正六边形,侧面是等腰三角形的棱锥
C
6.
知1-练
感悟新知
7.
如图是一些完全相同的小正方体搭成的几何体的三视图,则这个几何体只能是( )
A
知1-练
感悟新知
8.
一个几何体的三视图如图所示,该几何体是( )
D
知识点
由三视图确定组合体的数据
知2-讲
感悟新知
2
例 3
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状是图中的( )
D
知2-练
感悟新知
俯视图中,第一列最高有3个小立方块,第二列最高有2个小立方块,第三列最高有3个小立方块,因此,主视图从左到右可看到的小立方块个数依次为3、2、3,故选D.
导引:
知2-讲
总 结
感悟新知
由一种视图猜想另一种视图,中间也是跳跃一
步——还原几何体.先还原几何体,再确定另一种
视图.
随机事件
知2-练
感悟新知
1.
由若干个相同的小正方体组合而成的一个几何体
的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.3
B.4
C.5
D.6
C
知2-练
感悟新知
2.
一张桌子上摆放有若干个大小、形状完全相同的
碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
B
随机事件
知2-练
感悟新知
3.
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
A.
B.7
C.9
D.10
B
课堂小结
由三视图到几何体
1.通过这节课的学习,你有哪些收获?
2.由立体图形的三视图想象立体图形的形状时,你
有什么好的看法?与同伴交流一下.
