冀教版数学九年级下册32.2.1 由几何体到三视图课件(30张ppt)
文档属性
| 名称 | 冀教版数学九年级下册32.2.1 由几何体到三视图课件(30张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-12 09:14:33 | ||
图片预览







文档简介
(共30张PPT)
32.2 视图
第三十二章 投影与视图
课时导入
回顾与思考
这首诗教会
了我们怎样观察
物体(横看、侧看、
近看、身处其中
看),这类似于本
节课所研究的内
容——三视图.
知识点
几何体的三视图
知1-讲
感悟新知
1
当我们从某一方向观察一个物体时,所看到的平面图形
叫做物体的一个视图.
在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面 内得到的由上向下观察物体的视图,叫做俯视
图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
知1-讲
感悟新知
速记口诀:
视图来源正投影,
三个方向实物成,
由前向后主视图,
由上向下俯视图,
由左向右左视图,
统称物体三视图.
知1-练
感悟新知
例 1
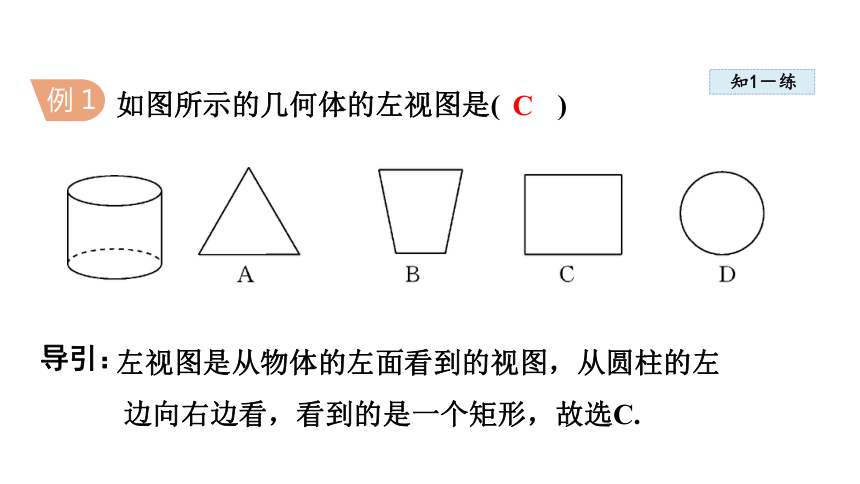
如图所示的几何体的左视图是( )
左视图是从物体的左面看到的视图,从圆柱的左
边向右边看,看到的是一个矩形,故选C.
C
导引:
知1-讲
总 结
感悟新知
单个几何体的三视图直接根据常见的几何体三
视图中识别.
知1-练
感悟新知
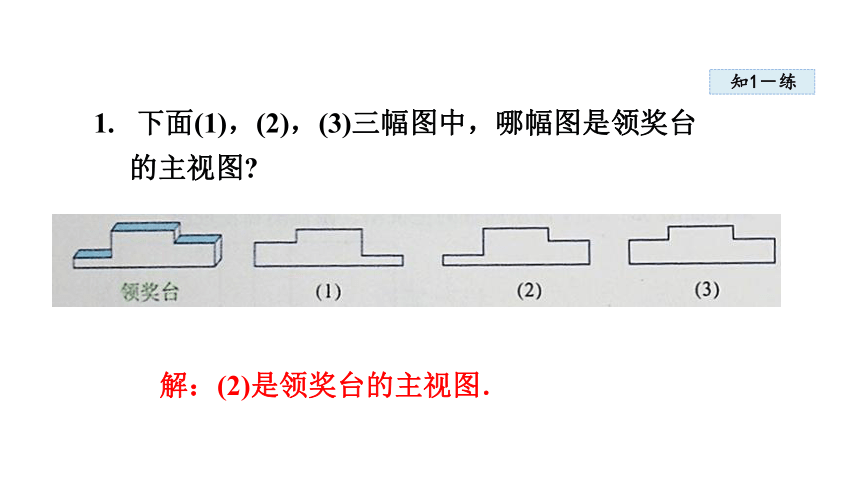
1. 下面(1),(2),(3)三幅图中,哪幅图是领奖台
的主视图
解:(2)是领奖台的主视图.
知1-练
感悟新知
2.
如图是由四个相同的小正方体组成的几何体,则它的主视图为( )
A
知1-练
感悟新知
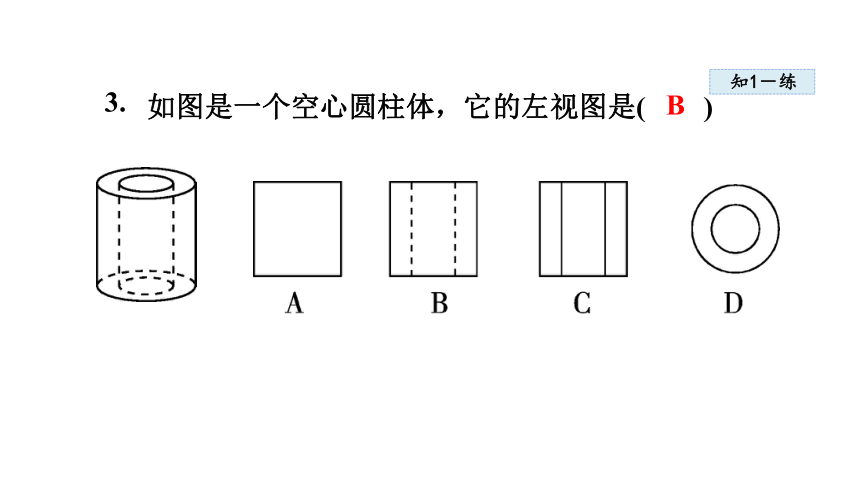
3.
如图是一个空心圆柱体,它的左视图是( )
B
知1-练
感悟新知
4.
如图是一个正六棱柱的茶叶盒,其俯视图为( )
B
知1-练
感悟新知
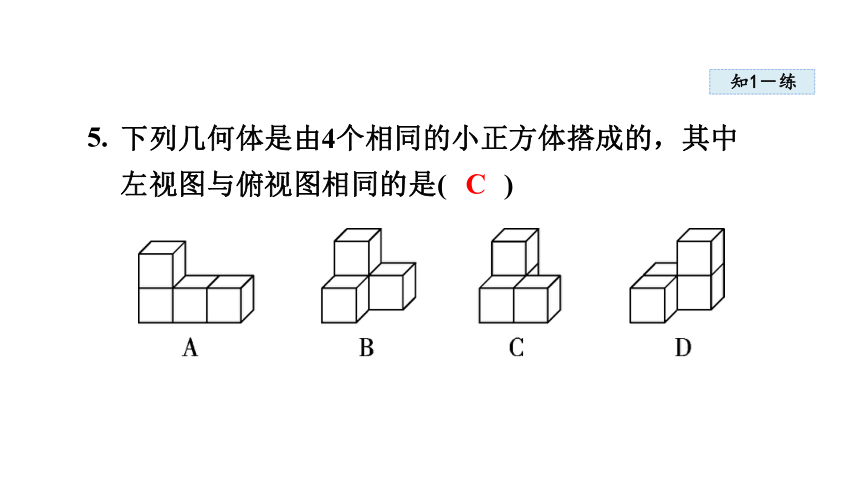
5.
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
C
知1-练
感悟新知
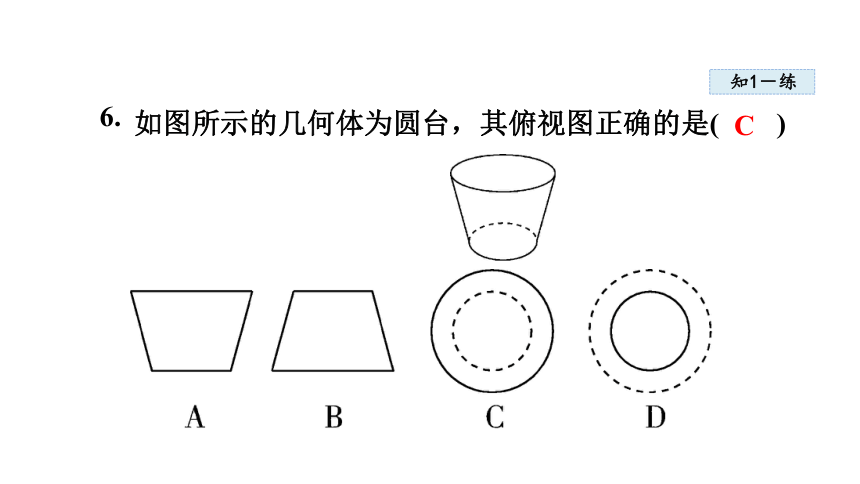
6.
如图所示的几何体为圆台,其俯视图正确的是( )
C
知1-练
感悟新知
7.
下面几个几何体中,其主视图不是中心对称图形的是( )
C
知1-练
感悟新知
8.
将如图所示的图形绕AB边所在直线旋转一周,所得几何体的俯视图为( )
B
知识点
画几何体的三视图
知2-讲
感悟新知
2
如图,将三个投影面展开在一个平 面内,得到
这一物体的一张三视图(由主视图、俯视图和左视图
组成).三视图中的各视
图,分别从不 同方面
表示物体的形状,三
者合起来能够较全面
地 反映物体的形状.
知2-讲
感悟新知
主视图
左视图
俯视图
长
宽
高
长
高
宽
长对正,主视俯视长相等且对正
高平齐,俯视左视宽相等且对应
宽相等.主视左视高相等且平齐
高
长
宽
知2-讲
感悟新知
速记口诀:
视图位置要摆明,
画图规则要记清.
主俯视图长对正,
左俯视图宽相等.
主左视图高平齐,
实线虚线应分清.
知2-练
感悟新知
例2
画出如图所示圆柱的主视图、俯视图和左视图.
知2-练
感悟新知
如图,圆柱的主视图是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径;它的俯视图是一个圆,圆的直径
等于圆柱底面圆的直径;它的
左视图也是一个长方形,长 方
形的长和宽分别等于圆柱的高
和圆柱底面圆的直径.
解:
知2-讲
总 结
感悟新知
不论是画单个几何体的三视图还是组合几何体的三视图,都必须注意两点:
一是遵循“长对正,高平齐,宽相等”的原则;
二是看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
随机事件
知2-练
感悟新知
1. 按要求画出下列几何体的视图.
解:如图所示.
知2-练
感悟新知
2. 如图,由5个相同小正方体构成的组合体的俯视
图为__________.
(4)
随机事件
知2-练
感悟新知
3.
如图,画出底面为正五边形的无棱柱的主视图、俯视图和左视图.
解:如图所示.
随机事件
知2-练
感悟新知
4.
如图,画出这个组合体(下部是正方体,上部是球,球的直径等于正 方体的棱长)的主视图、俯视图和左视图.
解:如图所示.
随机事件
知2-练
感悟新知
下面关于正六棱柱的视图(主视图、左视图、俯视图)
中,画法错误的是( )
A
5.
随机事件
知2-练
感悟新知
6.
如图,添线补全各
物体的三视图.
解:(1)主视图正确,左视图、
俯视图如图①所示.
(2)主视图正确,左视图、
俯视图如图②所示.
随机事件
知2-练
感悟新知
7.
画出如图所示立体图形的三
视图.(相当于在桌面的中间
靠后放着一个盒子)
解:三视图如图所示.
课堂小结
由几何体到三视图
1. 三视图是指主视图、左视图与俯视图.
2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高
平齐”与俯视图“宽相等”.
课堂小结
有几何体到三视图
如图是一个由3个相同的正方体组成的立体图形,它的三视图是( )
A
课堂小结
有几何体到三视图
易错点:画图时忽视被遮挡部分的轮廓线.
32.2 视图
第三十二章 投影与视图
课时导入
回顾与思考
这首诗教会
了我们怎样观察
物体(横看、侧看、
近看、身处其中
看),这类似于本
节课所研究的内
容——三视图.
知识点
几何体的三视图
知1-讲
感悟新知
1
当我们从某一方向观察一个物体时,所看到的平面图形
叫做物体的一个视图.
在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面 内得到的由上向下观察物体的视图,叫做俯视
图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
知1-讲
感悟新知
速记口诀:
视图来源正投影,
三个方向实物成,
由前向后主视图,
由上向下俯视图,
由左向右左视图,
统称物体三视图.
知1-练
感悟新知
例 1
如图所示的几何体的左视图是( )
左视图是从物体的左面看到的视图,从圆柱的左
边向右边看,看到的是一个矩形,故选C.
C
导引:
知1-讲
总 结
感悟新知
单个几何体的三视图直接根据常见的几何体三
视图中识别.
知1-练
感悟新知
1. 下面(1),(2),(3)三幅图中,哪幅图是领奖台
的主视图
解:(2)是领奖台的主视图.
知1-练
感悟新知
2.
如图是由四个相同的小正方体组成的几何体,则它的主视图为( )
A
知1-练
感悟新知
3.
如图是一个空心圆柱体,它的左视图是( )
B
知1-练
感悟新知
4.
如图是一个正六棱柱的茶叶盒,其俯视图为( )
B
知1-练
感悟新知
5.
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
C
知1-练
感悟新知
6.
如图所示的几何体为圆台,其俯视图正确的是( )
C
知1-练
感悟新知
7.
下面几个几何体中,其主视图不是中心对称图形的是( )
C
知1-练
感悟新知
8.
将如图所示的图形绕AB边所在直线旋转一周,所得几何体的俯视图为( )
B
知识点
画几何体的三视图
知2-讲
感悟新知
2
如图,将三个投影面展开在一个平 面内,得到
这一物体的一张三视图(由主视图、俯视图和左视图
组成).三视图中的各视
图,分别从不 同方面
表示物体的形状,三
者合起来能够较全面
地 反映物体的形状.
知2-讲
感悟新知
主视图
左视图
俯视图
长
宽
高
长
高
宽
长对正,主视俯视长相等且对正
高平齐,俯视左视宽相等且对应
宽相等.主视左视高相等且平齐
高
长
宽
知2-讲
感悟新知
速记口诀:
视图位置要摆明,
画图规则要记清.
主俯视图长对正,
左俯视图宽相等.
主左视图高平齐,
实线虚线应分清.
知2-练
感悟新知
例2
画出如图所示圆柱的主视图、俯视图和左视图.
知2-练
感悟新知
如图,圆柱的主视图是一个长方形,长方形的长和宽分别等于圆柱的高和圆柱底面圆的直径;它的俯视图是一个圆,圆的直径
等于圆柱底面圆的直径;它的
左视图也是一个长方形,长 方
形的长和宽分别等于圆柱的高
和圆柱底面圆的直径.
解:
知2-讲
总 结
感悟新知
不论是画单个几何体的三视图还是组合几何体的三视图,都必须注意两点:
一是遵循“长对正,高平齐,宽相等”的原则;
二是看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
随机事件
知2-练
感悟新知
1. 按要求画出下列几何体的视图.
解:如图所示.
知2-练
感悟新知
2. 如图,由5个相同小正方体构成的组合体的俯视
图为__________.
(4)
随机事件
知2-练
感悟新知
3.
如图,画出底面为正五边形的无棱柱的主视图、俯视图和左视图.
解:如图所示.
随机事件
知2-练
感悟新知
4.
如图,画出这个组合体(下部是正方体,上部是球,球的直径等于正 方体的棱长)的主视图、俯视图和左视图.
解:如图所示.
随机事件
知2-练
感悟新知
下面关于正六棱柱的视图(主视图、左视图、俯视图)
中,画法错误的是( )
A
5.
随机事件
知2-练
感悟新知
6.
如图,添线补全各
物体的三视图.
解:(1)主视图正确,左视图、
俯视图如图①所示.
(2)主视图正确,左视图、
俯视图如图②所示.
随机事件
知2-练
感悟新知
7.
画出如图所示立体图形的三
视图.(相当于在桌面的中间
靠后放着一个盒子)
解:三视图如图所示.
课堂小结
由几何体到三视图
1. 三视图是指主视图、左视图与俯视图.
2. 画物体三视图的具体步骤为:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图的正右方画出左视图,注意与主视图“高
平齐”与俯视图“宽相等”.
课堂小结
有几何体到三视图
如图是一个由3个相同的正方体组成的立体图形,它的三视图是( )
A
课堂小结
有几何体到三视图
易错点:画图时忽视被遮挡部分的轮廓线.
