24.1.3 弧、弦、圆心角(1)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 232.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-09 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
弧、弦、圆心角、
弦心距 (1)
引入
如图,OA、OB是⊙O的两条半
径,∠AOB有什么特点?
O
A
B
(1)顶点在圆心;
(2)两边是半径。
归纳
圆心角的定义:
O
A
B
顶点在圆心,两边分别是圆的半
径的角叫做圆心角。
引入
如图,AB是⊙O的弦,过圆心O
作OC⊥AB于C,OC有什么特点?
(1)过圆心;
(2)垂直弦。
O
A
B
C
归纳
弦心距的定义:
圆心到弦的距离叫做弦心距。
O
A
B
C
引入
如图,AB是⊙O的弦,过圆心O
作OC⊥AB于C,连接OA、OB。观察
弦AB、AB、圆心角∠AOB、弦AB的
弦心距OC之间的关系。
O
A
B
C
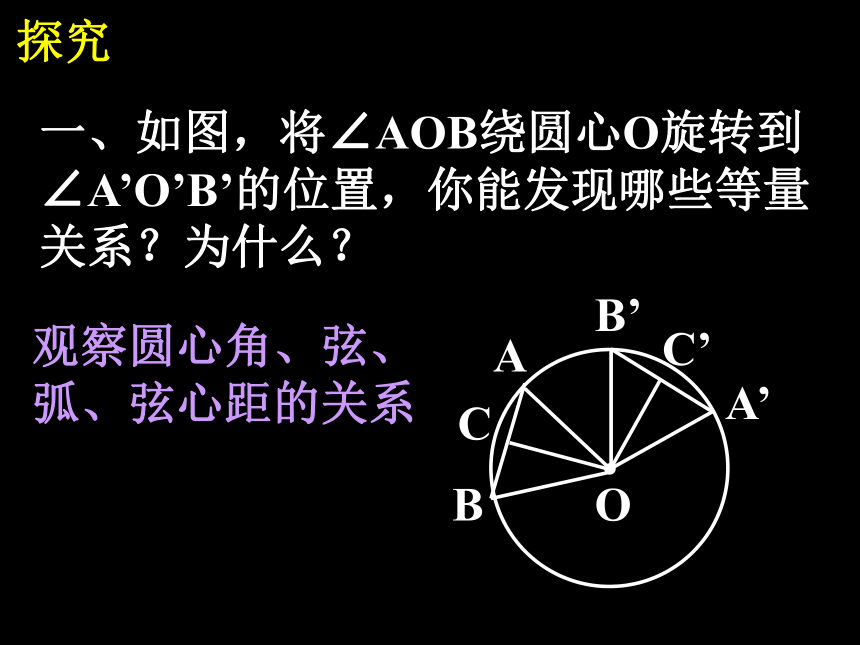
探究
一、如图,将∠AOB绕圆心O旋转到
∠A’O’B’的位置,你能发现哪些等量
关系?为什么?
O
A
B
B’
A’
C
C’
观察圆心角、弦、
弧、弦心距的关系
归纳
O
A
B
B’
A’
C
C’
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等,所对
弦的弦心距也相等。
在同圆或等圆中,
同圆或等圆的定理:
归纳
O
A
B
B’
A’
C
C’
(1)圆心角;
(2)圆心角所对的弧;
(3)圆心角所对的弦;
(4)圆心角所对弦的弦心距.
其中有一组量相等,
其他三组量也相等
知一得三
同圆或等圆的“知一得三”:
1、如图,AB、CD是⊙O的两条弦,
OE、OF分别是AB、CD的弦心距。
巩固
O
A
B
C
D
E
F
(1)如果AB=CD,
那么 ;
(2)如果AB=CD,
那么 ;
(3)如果∠AOB=∠COD,
那么 ;
(4)如果OE=OF,
那么 ;
例1、如图,在⊙O中,AB=AC,
∠ACB=60°。
求证:∠AOB=∠BOC=∠AOC。
范例
O
A
B
C
巩固
2、如图,AB是⊙O的直径,BC=CD
=DE,∠COD=35°。
求∠ AOE的度数。
O
A
B
C
E
D
巩固
3、如图,A、B是⊙O上的两点,
∠AOB=120°,C是AB的中点,求证
四边形OACB是菱形。
O
A
B
C
范例
例2、如图,O是∠CAE的平分线上的
一点,⊙O分别交∠CAE的两边于C、
B和D、E。
求证:(1)BC=DE;
(2)AC=AE。
O
A
B
C
D
E
巩固
4、已知:如图,在⊙O中,AD=BC。
求证:AB=CD。
O
A
B
C
D
巩固
5、已知:如图,⊙O是两条弦AB和
CD相交于点P,且OP平分∠BPD。
求证:AD=BC。
O
A
B
C
D
P
小结
同圆或等圆的“知一得三”:
(1)圆心角;
(2)圆心角所对的弧;
(3)圆心角所对的弦;
(4)圆心角所对弦的弦心距.
其中有一组量相等,其他三组量也相等
知一得三
弧、弦、圆心角、
弦心距 (1)
引入
如图,OA、OB是⊙O的两条半
径,∠AOB有什么特点?
O
A
B
(1)顶点在圆心;
(2)两边是半径。
归纳
圆心角的定义:
O
A
B
顶点在圆心,两边分别是圆的半
径的角叫做圆心角。
引入
如图,AB是⊙O的弦,过圆心O
作OC⊥AB于C,OC有什么特点?
(1)过圆心;
(2)垂直弦。
O
A
B
C
归纳
弦心距的定义:
圆心到弦的距离叫做弦心距。
O
A
B
C
引入
如图,AB是⊙O的弦,过圆心O
作OC⊥AB于C,连接OA、OB。观察
弦AB、AB、圆心角∠AOB、弦AB的
弦心距OC之间的关系。
O
A
B
C
探究
一、如图,将∠AOB绕圆心O旋转到
∠A’O’B’的位置,你能发现哪些等量
关系?为什么?
O
A
B
B’
A’
C
C’
观察圆心角、弦、
弧、弦心距的关系
归纳
O
A
B
B’
A’
C
C’
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等,所对
弦的弦心距也相等。
在同圆或等圆中,
同圆或等圆的定理:
归纳
O
A
B
B’
A’
C
C’
(1)圆心角;
(2)圆心角所对的弧;
(3)圆心角所对的弦;
(4)圆心角所对弦的弦心距.
其中有一组量相等,
其他三组量也相等
知一得三
同圆或等圆的“知一得三”:
1、如图,AB、CD是⊙O的两条弦,
OE、OF分别是AB、CD的弦心距。
巩固
O
A
B
C
D
E
F
(1)如果AB=CD,
那么 ;
(2)如果AB=CD,
那么 ;
(3)如果∠AOB=∠COD,
那么 ;
(4)如果OE=OF,
那么 ;
例1、如图,在⊙O中,AB=AC,
∠ACB=60°。
求证:∠AOB=∠BOC=∠AOC。
范例
O
A
B
C
巩固
2、如图,AB是⊙O的直径,BC=CD
=DE,∠COD=35°。
求∠ AOE的度数。
O
A
B
C
E
D
巩固
3、如图,A、B是⊙O上的两点,
∠AOB=120°,C是AB的中点,求证
四边形OACB是菱形。
O
A
B
C
范例
例2、如图,O是∠CAE的平分线上的
一点,⊙O分别交∠CAE的两边于C、
B和D、E。
求证:(1)BC=DE;
(2)AC=AE。
O
A
B
C
D
E
巩固
4、已知:如图,在⊙O中,AD=BC。
求证:AB=CD。
O
A
B
C
D
巩固
5、已知:如图,⊙O是两条弦AB和
CD相交于点P,且OP平分∠BPD。
求证:AD=BC。
O
A
B
C
D
P
小结
同圆或等圆的“知一得三”:
(1)圆心角;
(2)圆心角所对的弧;
(3)圆心角所对的弦;
(4)圆心角所对弦的弦心距.
其中有一组量相等,其他三组量也相等
知一得三
同课章节目录
